Основные законы распределения непрерывных случайных величин

1. Основные законы распределения непрерывных случайных величин

Презентация для студентов
АКб 2

2.

Непрерывная СВ
НСВ называется такая величина,
возможные значения которой
непрерывно заполняют некоторый
интервал (конечный или бесконечный).
Число всех возможных значений НСВ
бесконечно.
Пример: Случайное отклонение по дальности
точки падения снаряда от цели.

3.

Функция распределения НСВ
Функцией распределения называют F(x),
определяющую для каждого значения x
вероятность того, что СВХ примет значение,
меньшее х, т.е. согласно определению
F(x)=P(X<x)
F(x) определяет и ДСВ и НСВ. F(x) также
называют интегральной функцией
распределения.

4.

Функция распределения НСВ
Свойства функции распределения:
1. 0 F(x) 1
2. если
x2 x1 , то
F(x2) F(x1)
(
a
x
b
)
F
(
b
)
F
(
a
)
следствие: P
3.
Если все возможные значения x СВХ принадлежат интервалу (a;b),
то при a<=a F(x)=0, а при x>=b F(x)=1
Следствие:
lim F ( x) 0
x
lim F ( x) 1
x
Функция распределения непрерывна слева

5.

Функция плотности распределения
НСВ
Функцией плотности распределения вероятностей называют первую
производную от функции F(x), то есть f(x)=F`(x). f(x) называют
дифференциальной функцией. Вероятность того, что НСВХ
примет значения, принадлежащие интервалу (a;b) вычисляемые
b
по формуле
P(a < x < b)= f(x)dx
a
Зная плотность распределения,
можно найти функцию
x
распределения
F(x)= f(x)dx
Свойства:
1.
2.
f (x) 0
в частности, если все возможные значения
f (x)dx 1,СВ
принадлежат (a;b), то
f (x)dx 1
b
a

6.

Числовые хар-ки НСВ
Математическое ожидание НСВХ, все возможные значения которой
принадлежат интервалу (a;b), определяется равенством:
b
M(X) = x f(x)dx
a
Дисперсия НСВХ, все возможные
значения которой принадлежат интервалу
(a;b), определяется равенством:
b
D(X) = (x M(x)) f(x)dx
2
a
При решении задач применима формула:
b
D(X) = x f(x)dx (M(X))
a
2

7.

Числовые хар-ки НСВ
Среднеквадратичное отклонение определяется так же, как и для ДСВ:
(X
) D
(X
)
Начальный момент k-ого порядка НСВ определяется равенством:
x f(x)dx
b
k
k
a
M(X)
1
M
(
X
)
xf(
x
)
dx
b
2
2
2
a

8.

Числовые хар-ки НСВ
Центральный момент k-ого порядка НСВХ, все возможные значения которой
принадлежат интервалу (a:b), определяется равенством:
(
x
M
(
x
))
f(
x
)
dx
b
k
k
a
1
0
D(X)
3
2
2
3
1
3
3
12
4
6
4
13
4
3
2
2
1
4
1

9.

Числовые хар-ки НСВ
Если все возможные значения НСВХ принадлежат всей
числовой оси ОХ, то во всех вышеуказанных формулах
определенный интеграл заменяется несобственным
интегралом с бесконечными нижним и верхним пределами

10.

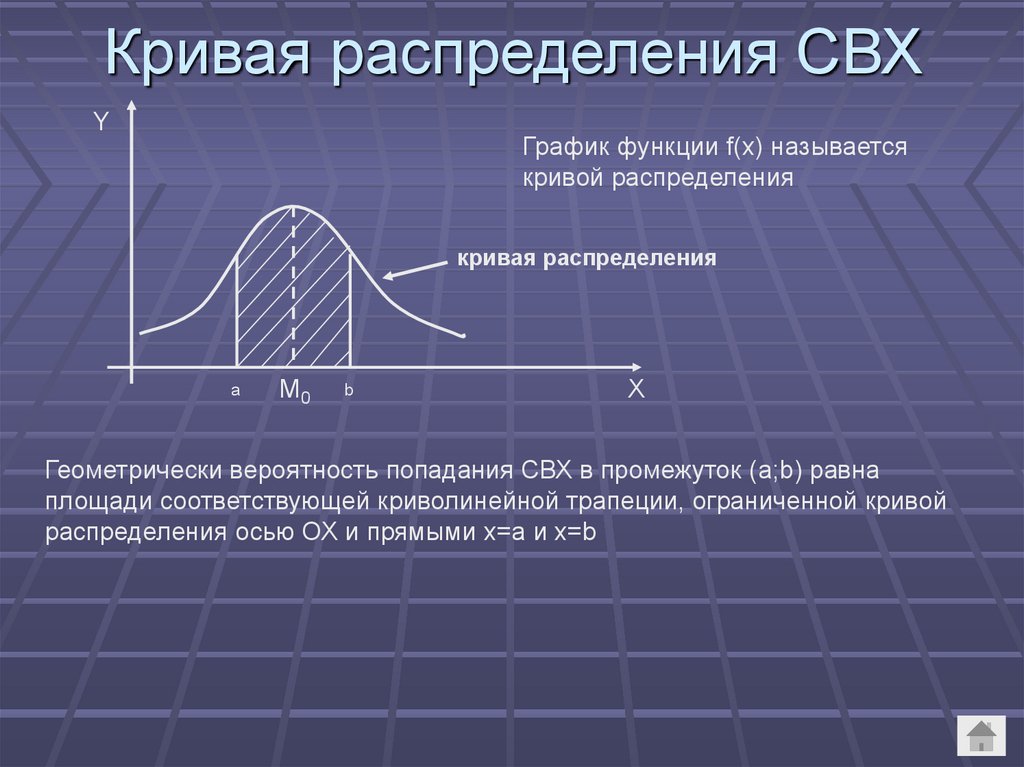
Кривая распределения СВХ
Y
График функции f(x) называется
кривой распределения
кривая распределения
a
М0
b
X
Геометрически вероятность попадания СВХ в промежуток (a;b) равна
площади соответствующей криволинейной трапеции, ограниченной кривой
распределения осью ОХ и прямыми x=a и x=b

11.

Мода
Модой ДСВХ называется ее наиболее вероятное значение. Модой НСВХ
называется такое ее значение M0, при котором плотность распределения
максимальная.
Для нахождения моды НСВ необходимо найти максимум функции с помощью
первой или второй производной.
X
1
2
3
P
0.1
0.6
0.3
M0=2, т.к. 0.1<0.6>0.3
Геометрически мода является абсциссой той точки кривой или полигона
распределения, ордината которой максимальна
Y
a
М0
b
X

12.

Медиана
Медианой НСВХ называется такое ее значение Ме, для
которого одинаково вероятно, окажется ли случайная величина
больше или меньше Ме, т.е. P(x< Ме)=P(x> Ме)=0.5
Ордината, проведенная к точке с абсциссой, равной Ме,
делит пополам площадь, ограниченную кривой или
полигоном распределения. Если прямая x=a
является осью симметрии кривой распределения
y=f(x), то М0=Ме=М(Х)=a

13.

Равномерное распределение
плотности
Равномерным называется распределение таких СВ, все значения которых лежат на некотором
отрезке (a;b) и имеют постоянную плотность вероятности на этом отрезке
Математическое ожидание, дисперсия, среднеквадратичное
отклонение равномерно распределенной СВ:
Y
h
a b
M
(X)
2
a
(a b
)
D
(X
)
12
2
(X) b2 3a
b
0,x a
f(x)
h,a x b
0,x b
h
1
b a
X

14.

X
Показательное распределение
0, x 0
f ( x) =
x
e
, x 0
1
M(X)=
1
D(X) 2
1
σ(X)=

15.

Нормальный закон распределения.
Функция Лапласа
Нормальный закон распределения характеризуется плотностью
2
(x
a
)
Кривая распределения симметрична
2
2
относительно прямой x=a.
1
f(
x
)
e
2
Y
Кривая Гаусса, нормальная
кривая
Максимальная ордината при x=a
равна
1
2
1) f (x) 0
2) f (x) 1
x=a
M(X) a
(X) D(X)
M0 a Me
X
Ось абсцисс является асимптотой
кривой y=f(x)
Ф(x) - Функция Лапласа
x
1
t 2 /2
Ф(x)=
e
dt
2π 0