Похожие презентации:
Свойства логарифмов
1. Определение
Логарифмом положительного числа bпо основанию a, где а>0, а≠1
называется показатель степени, в
которую надо возвести число а,
чтобы получить b.
log a b x, a b,
x
a 0, a 1, b 0
2. Вычислить устно:
3. Вычислить устно:
1) log 2 642) log 4 16
3) log 1 3
1
4) log 5
25
3
5) log 6 36
6) log 25 5
7) log
8) log 3
2
2
9) log 2 64 log 4 16
10) log 2 12 log 2 3
27
4. Свойства логарифмов
5. Основное логарифмическое тождество
По определению логарифмаа
loga b
b
6.
a)2б)
log2 13
70
2
7
log2 5
log7 13
13
70
14
5
13 1
в)
0,25
52
52 4
7.
.Вычислите:
3 log 3 18;
3 5log 3 2;
5 log 5 16;
0,3 2log 0,3 6;
10 log 10 2;
(1/4) log(1/4) 6;
8 log 2 5;
9 log 3 12.
8. Решить устно:
9. Вычислить устно:
10. 1. Логарифм произведения равен сумме логарифмов множителей:
log x ab log x a log x bПример :
log 72 log 3 log6 (72 3) log 216 3
6
6
6
a ) log 12 4 log 12 36 log 12 (4 36)
log 12 144 log 12 12 2 2 log 12 12 2 1 2
11. Вычислите:
1. log18 2 + log18 92. log4 8 + log4 32
3. log32 2 + log32 2
4. lg 40 + lg 25
1)
2)
3)
4)
1
4
0,2
3
12.
2. Логарифм частного равен логарифмовделимого без логарифма делителя:
a
log x log x a log x b
b
Пример:
log 48 log 4
12
12
48
log
12 4
log 12
12
1
13. 3. Логарифм степени равен произведению показателя степени на логарифм ее основания:
log x a m log x am
Пример
log 125 log 125
5
5
1
2
1
log 5125 1,5
2
log 2 32 log 2 2 5 log 2 2 5 1 5
5
14.
4. Основание логарифма в степениlog a k
1
x log a x, a 0, x 0, a 1
k
Пример
1
1
1
log 16 2 log 24 2 log 2 2 1 0,25
4
4
4
15.
5. Переход от одного основания к другомуlog b x
1
log a x
log a x
log b a
log x a
16. Свойства логарифмов
1log
log 3 7
3 7
1
a) log
log 3 81 log 3 34 4 log 3 3 4 1 4
3 81
17. Свойства логарифмов
log 113 log 3 11 118. Частные свойства:
1)log a 1 = 0;2) log a a = 1;
3) log a (1/a) = - 1;
4) log a a m = m;
5) log a m a = 1/m.
19. Упражнение № 1. Вычислить
20. Решаем из учебника:
№290-294 (четные номера)21. Домашняя работа:
• П.16, (выучить свойствалогарифмов)
• №290-294 (нечетные номера)




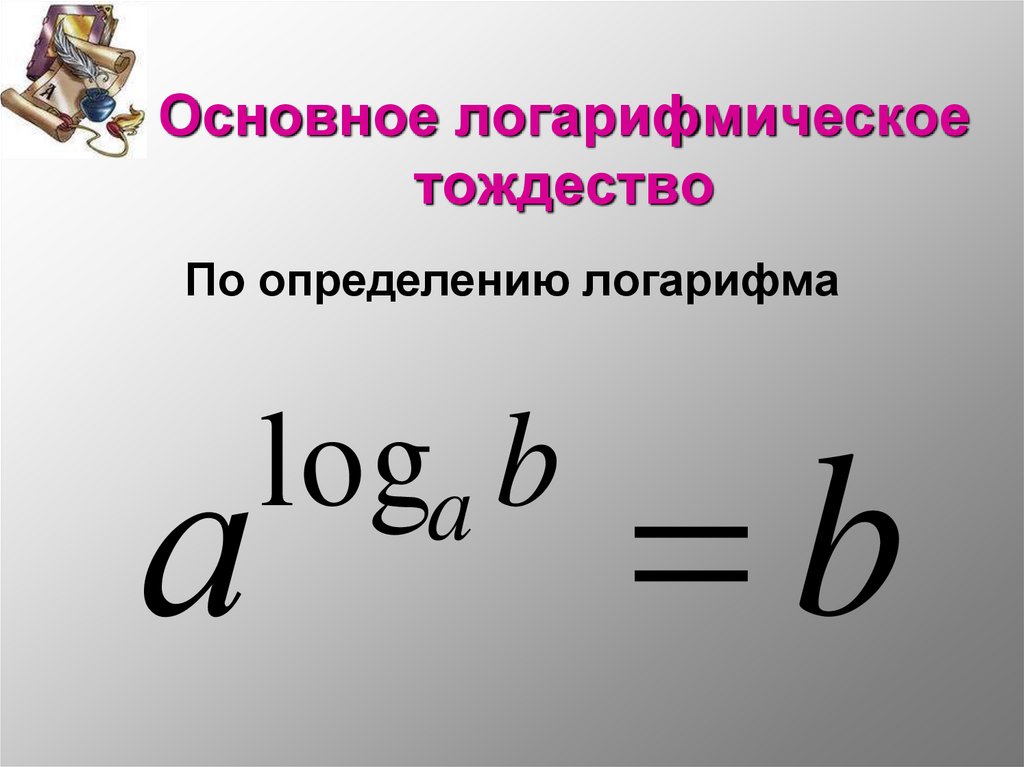
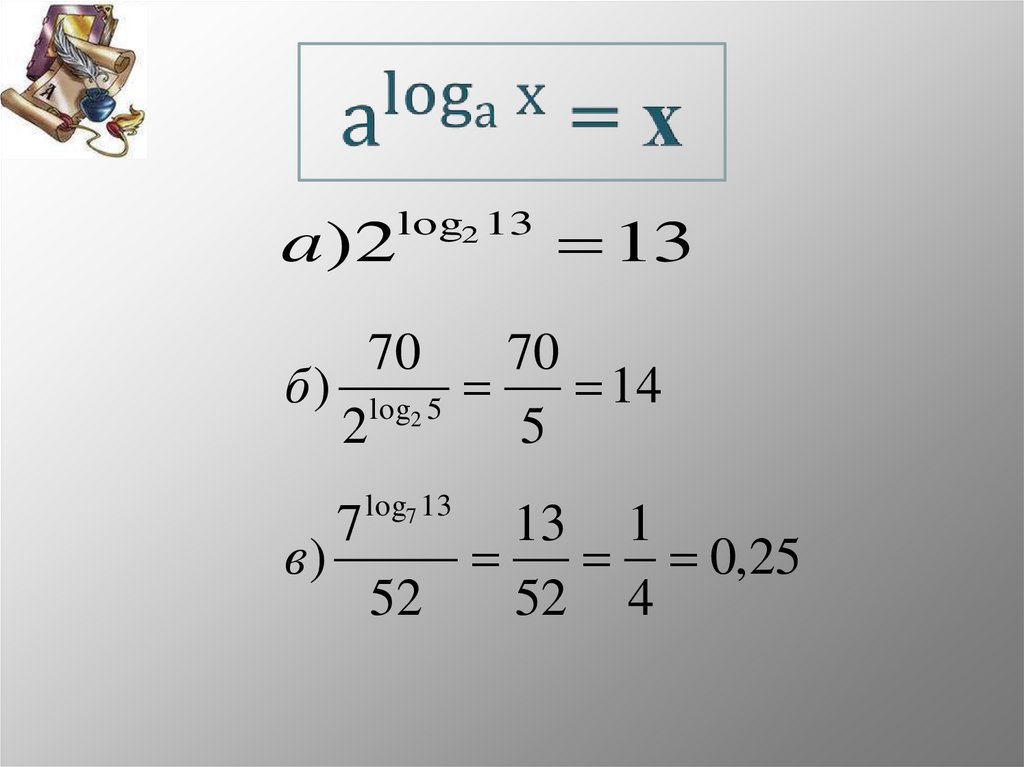















 Математика
Математика








