Похожие презентации:
Логарифмы и их свойства
1. Логарифмы и их свойства
2.
Логарифмы были придуманы для ускорения иупрощения вычислений.
Идея логарифма, т. е. идея выражать числа в
виде степени одного и того же основания,
принадлежит Михаилу Штифелю. Но во времена
Штифеля математика была не столь развита и
идея логарифма не нашла своего развития.
Логарифмы были изобретены позже
одновременно и независимо друг от друга
шотландским учёным Джоном Непером(15501617) и швейцарцем Иобстом Бюрги(1552-1632).
Джон Непер
В1614г. была опубликована работа Непера под названием «Описание
удивительной таблицы логарифмов»
Слово «логарифм» введено Непером, происходит от греческих
слов logoz и ariumoz - оно означает буквально “числа отношений”.
3.
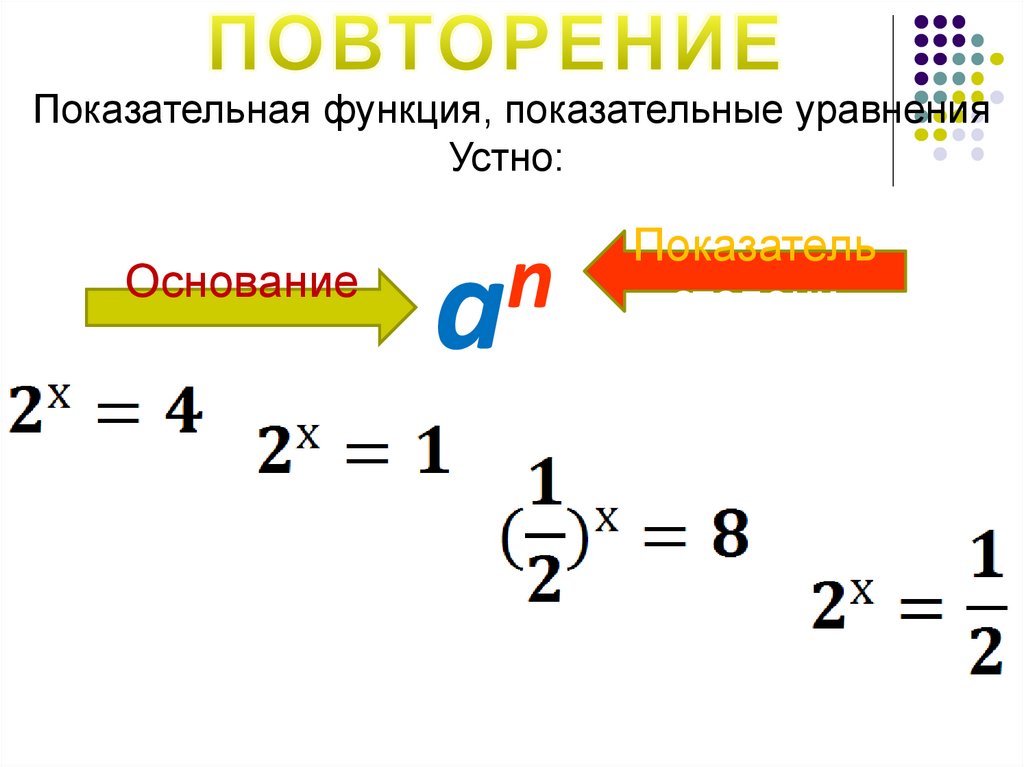
Показательная функция, показательные уравненияУстно:
Основание
степени
n
a
Показатель
степени
4.
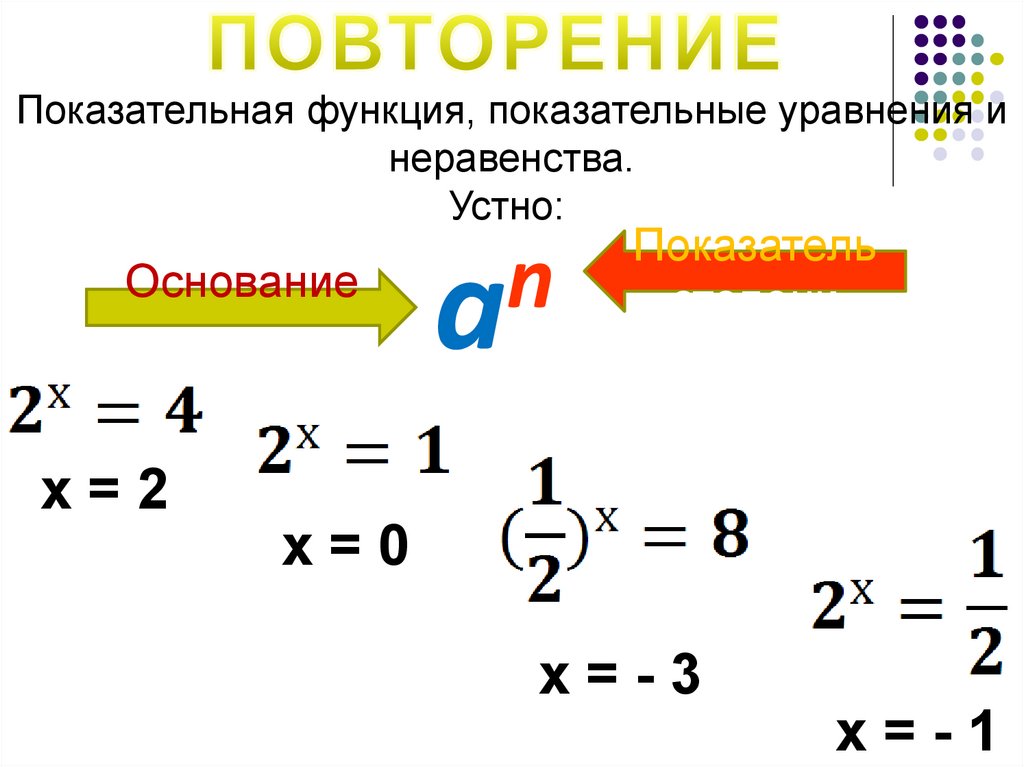
Показательная функция, показательные уравнения инеравенства.
Устно:
Основание
степени
х=2
n
a
Показатель
степени
х=0
х=-3
х=-1
5.
Логарифмом по основанию а от аргумента xназывают степень, в которую нужно возвести а,
чтобы получить х.
logax = b
Где:
а – основание логарифма;
х – аргумент (число или выражение под знаком логарифма);
b – значение логарифма.
Например:
log28 = 3
(логарифм по основанию 2 от числа 8 равен 3, поскольку 23 = 8 )
6.
1.Аргумент и основание логарифма всегда должны бытьбольше нуля. Это следует из определения степени с
рациональным показателем, к которому сводится
определение логарифма.
2.Основание должно быть отличным от единицы, поскольку
единица в любой степени все равно остается единицей.
loga x = b ⇒ x > 0, a > 0, a ≠ 1.
3.На число b (значение логарифма) никаких ограничений
не накладывается.
7. Определение логарифма числа
Логарифмом числа b по основанию aназывается показатель степени, в
которую нужно возвести основание a,
чтобы получить число b.
Формулу aˡ ͦ ᵍ ᵇ = b где a≠1,
a>0, b>0 называют основным
логарифмическим тождеством.
8.
Равенство справедливо при b > 0, a > 0, a ≠ 15
2
9.
10. Вычислить
log 2 2 1log 12 12 1
log 3 3 1
log 5 5 1
11. Вычислить
log 3 10
log 5 1
0
0
log 13 1 0
log 7 1
12. Вычислить
log 2 16log 2 2 4
4
log 2 64 log 2 2 6
6
log 3 27 log 3 3 3
3
log 3 81 log 3 3 4
4
13. Вычислить
11
log 2 2 1
log 2
2
1
1
log 3 3 1
log 3
3
1
3
log 2 log 2 2 3
8
14. Выполнить устно
3log3 18
5
log5 14
7
log7 8
15. Выполнить устно
3log3 18
=18
5
log5 14
=14
7
log7 8
=8
16.
Докажите, что:Доказательство:
17.
18. Основные свойства логарифмов
При любом a>0 (a≠1) и любых положительных xи y выполнены равенства:
logₐ x*y=logₐ x + logₐ y
logₐ x/y= logₐ x - logₐ y
logₐ xᵖ=p*logₐ x
для любого действительного p.
19. Свойства логарифмов
log a xy log a x log a ylog 24 3 log 24 8
log 24 24 1
20. Вычислить
log 12 4 log 12 3log 15 5 log 15 3
log 6 9 log 6 4
log 8 16 log 8 4
21. Вычислить
log 12 4 log 12 3 log 12 12 1log 15 5 log 15 3 log 15 15 1
log 6 9 log 6 4 log 6 36 2
log 8 16 log 8 4 log 8 64 2
22. Свойства логарифмов
log ax
log a x log a y
y
log 6 24 log 6 4
24
log 6
log 6 6 1
4
23. Вычислить
log 12 48 log 12 4log 5 75 log 5 3
log 2 12 log 2 3
log 10 50 log 10 5
24. Вычислить
log 12 48 log 12 4log 5 75 log 5 3
log 2 12 log 3
48
log 12 log 12 12 1
4
75
log 5
log 5 25 2
3
12
log 2
log 2 4 2
3
2
50
log 10
log 10 10 1
5
10
log 10 50 log 5
25. Свойства логарифмов
log n ba
1 log b
a
n
log a b n log a b
n
26. Свойства логарифмов
log a n b log a bn
log c b
log a b
log c a
27. Примеры
1log 36 6 log 6 2 6
2
3
log 5 125 log 5 5 3
1
log 16 64 log 2 4
6
3
2
4
2
6
28.
log a b n log a bn
29. Проблема
Обратите внимание - действия слогарифмами возможны только при
одинаковых основаниях! А если основания
разные!?
log 5 16 log 2 25
30. Переход к другому основанию
ТеоремаПусть дан логарифм loga b. Тогда
для любого числа c такого, что c > 0 и c ≠
1, верно равенство:
log c b
log a b
log c a
В частности, если положить c = b,
получим:
1
log a b
log c a
31. Логарифмические уравнения
32.
Логарифмом по основанию а от аргумента xназывают степень, в которую нужно возвести а,
чтобы получить х.
logax = b
Где:
а – основание логарифма;
х – аргумент (число или выражение под знаком логарифма);
b – значение логарифма.
Например:
log28 = 3
(логарифм по основанию 2 от числа 8 равен 3, поскольку 23 = 8 )
33.
1) log 5 16 log 2 25Воспользуемся сначала свойством
log a b n n log a b
log 5 2 4 log 2 52 4 log 5 2 2 log 2 5
Теперь перейдем к основанию 2
1
8
log 2 5 8
log 2 5
log a b
1
log c a
34.
35.
36.
37.
Логарифмическим уравнением называютуравнение, содержащее переменную под знаком
логарифма
Например:
log (x+6)=3
2
log x=1-x
3
Решить логарифмическое уравнение- это значит
найти все его корни или доказать , что их нет.
Надо помнить!!!!
Существуют логарифмы ТОЛЬКО
положительных чисел
ПРОВЕРКА или
ОДЗ(область допустимых значений)
38.
Способы решения логарифмическихуравнений
На основании определения логарифма
Логарифмом положительного числа b по
положительному и отличному от 1 основанию а
называют показатель степени, в которую
нужно возвести число а, чтобы получить
число b.
Решить уравнение
loga x = b, a > 0; a = 1.
ОДЗ. Х>0
имеет единственное решение
х=ab
39.
Решить уравнениеLog3(2x+1)=2
ОДЗ (ЗНАЮ!!!что существуют логарифмы только положительных чисел)
2x+1>0
2x+1=3²
2x=9-1
2x=8
x=4
Ответ : х=4
Или ПРОВЕРКА
Log3(2·4+1)= Log39=2
40. Простейшее логарифмическое уравнение
log a x b x a , x 0b
Например:
log 3 x 2
x 3
2
x 9;
Ответ : 9
( x 0) *
41. Решить уравнения
a) log 2 x 1 3в) lg x 3 2 lg 2 lg x
б) log 2 x 1 log 2 x 3 3 г) log 7 36 log 7 3x 12 log 7 4
42.
№1. Решить уравненияx 1 0
a) log 2 x 1 3
log 2 x 1 log 2 2
3
x 1*
x 1 8
x 7
Ответ : 7
43.
б) log 2 x 1 log 2 x 3 3log 2 x 1 x 3 log 2 23
x 1 0
x 1
x 1*
x 3 0 x 3
x2 4x 3 8
x2 4x 5 0
x1 1
x2 5 исключено *
Ответ :1
44. Решение уравнения под буквой в
в) lg x 3 2 lg 2 lg xx 3 0 x 3
x 0*
x 0
x 0
lg x 3 lg x lg 22
lg x x 3 lg 4
Согласно
свойству:
p log a b log a b p
x 2 3x 4
x 2 3x 4 0
x1 1;
x2 4;
исключено *
Ответ :1
Назад
45. Решение уравнения под буквой г
г ) log 7 36 log 7 3x 12 log 7 4log 7 3 x 12 log 7 36 log 7 4
36
log 7 3 x 12 log 7
4
3 x 12 9
3 x 12 0
3 x 12
x 4*
3 x 21
x 7;
Ответ : 7
Назад
46.
47.
48.
49.
№150.
№151.
№252.
№253.
№354.
№355.
№456.
№457.
№558.
№559.
№660.
№661.
№762.
№763.
64.
65.
66.
67.
loga
1 log b
b
n
a
n






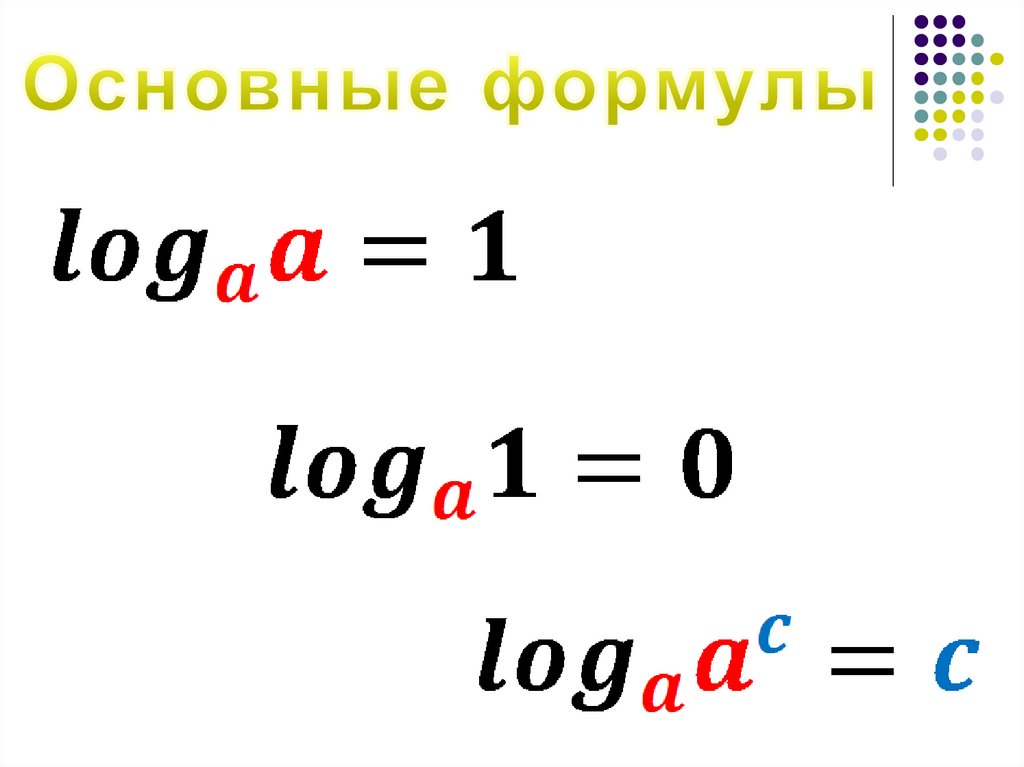

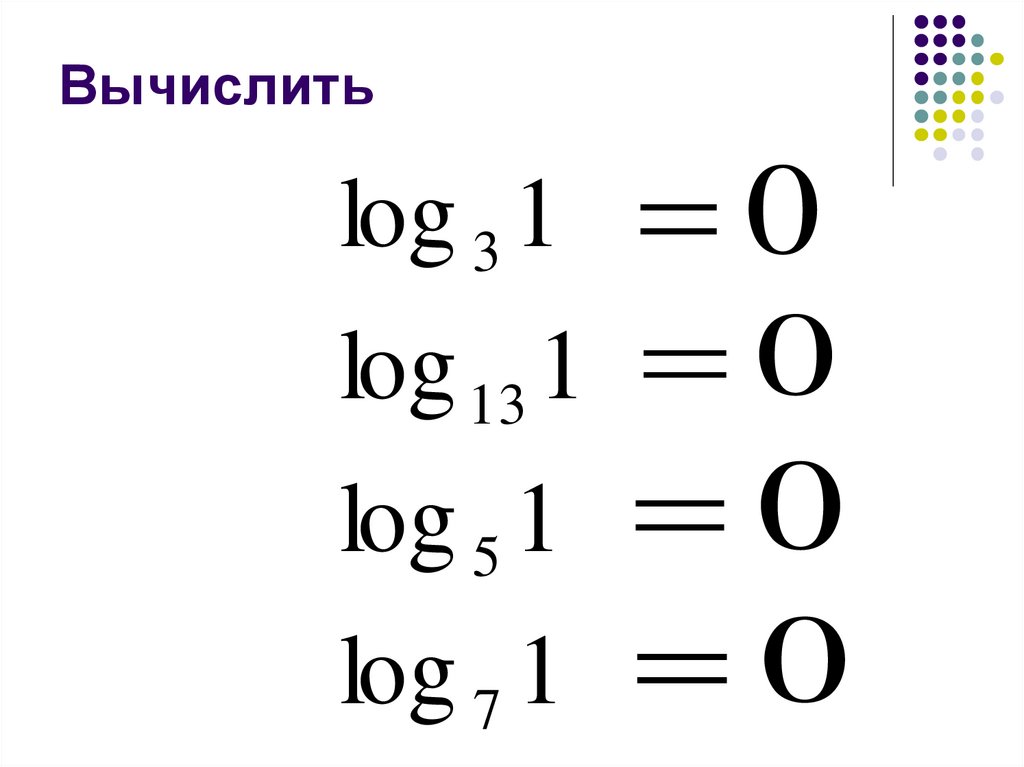
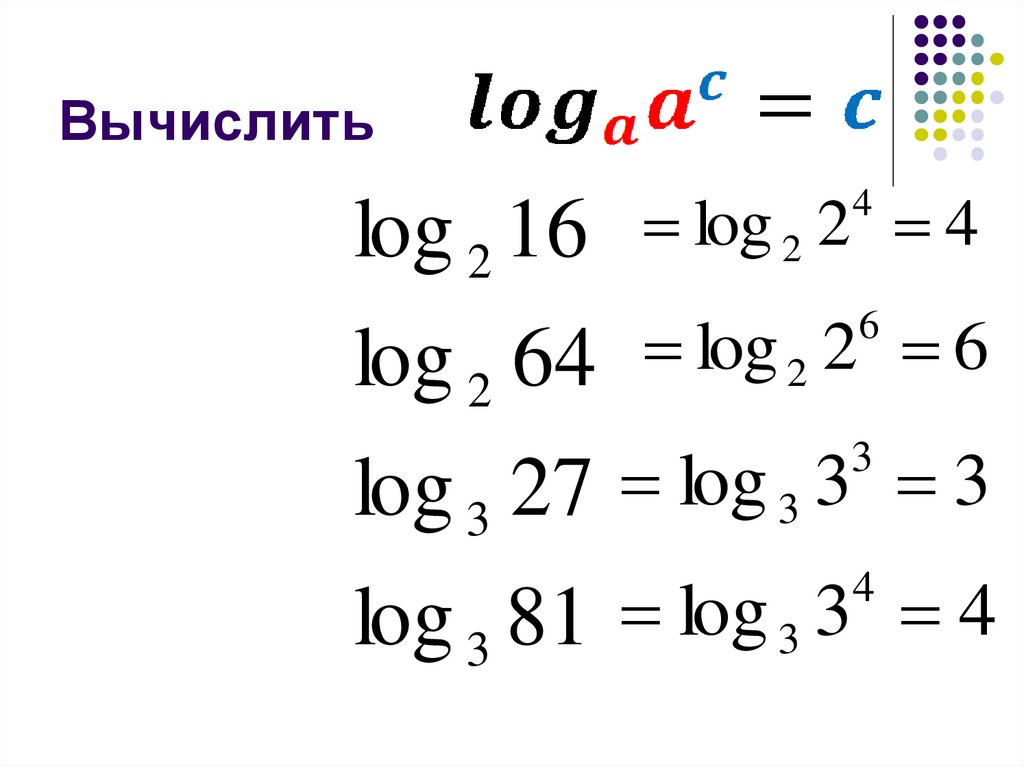












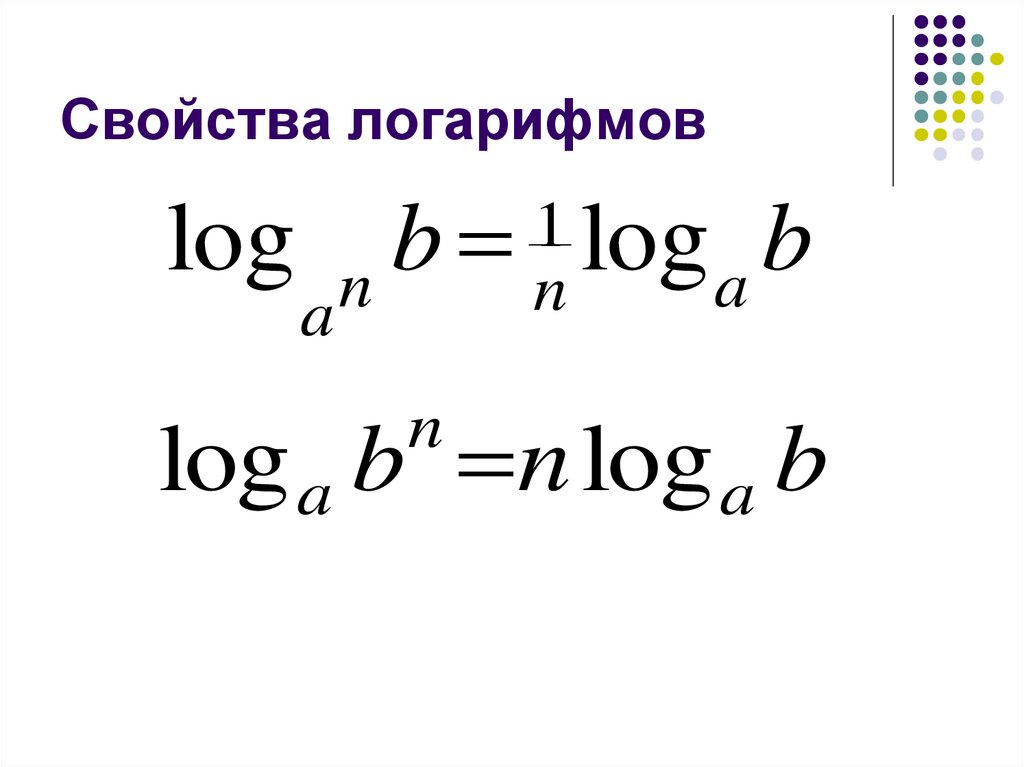


























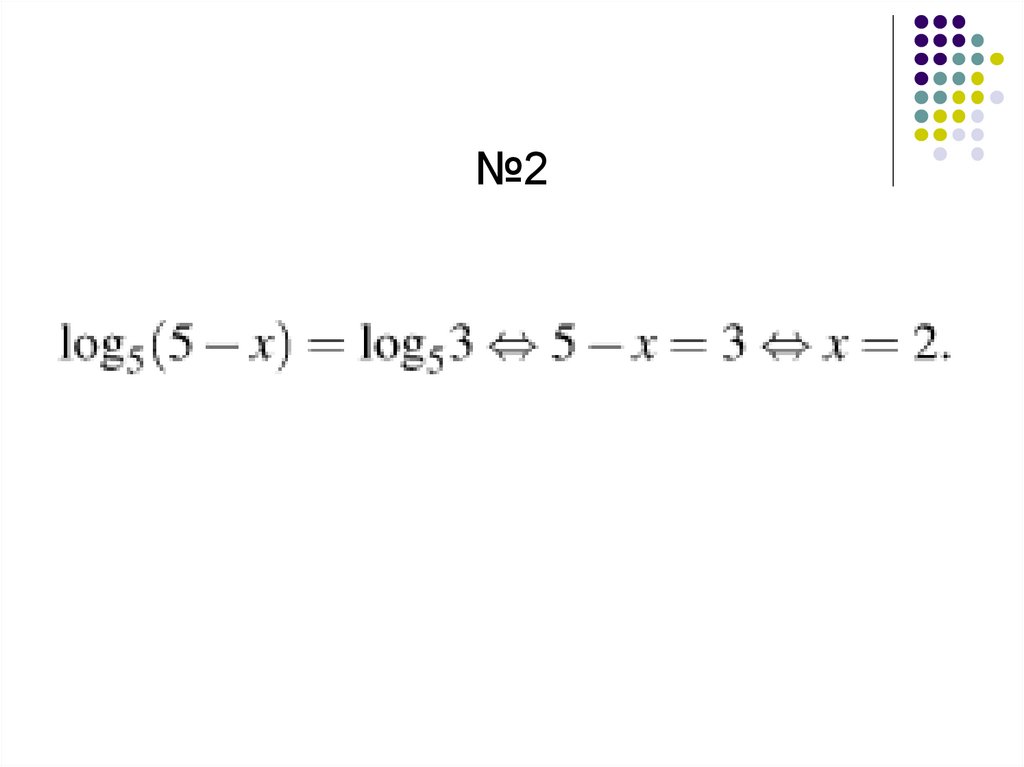





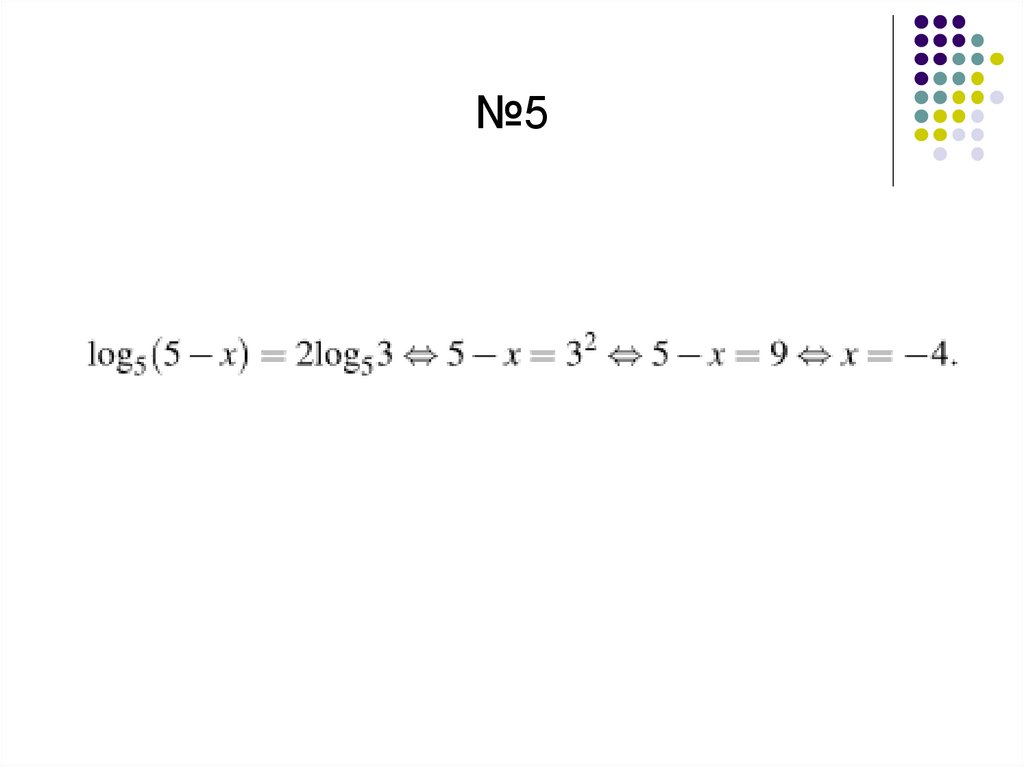



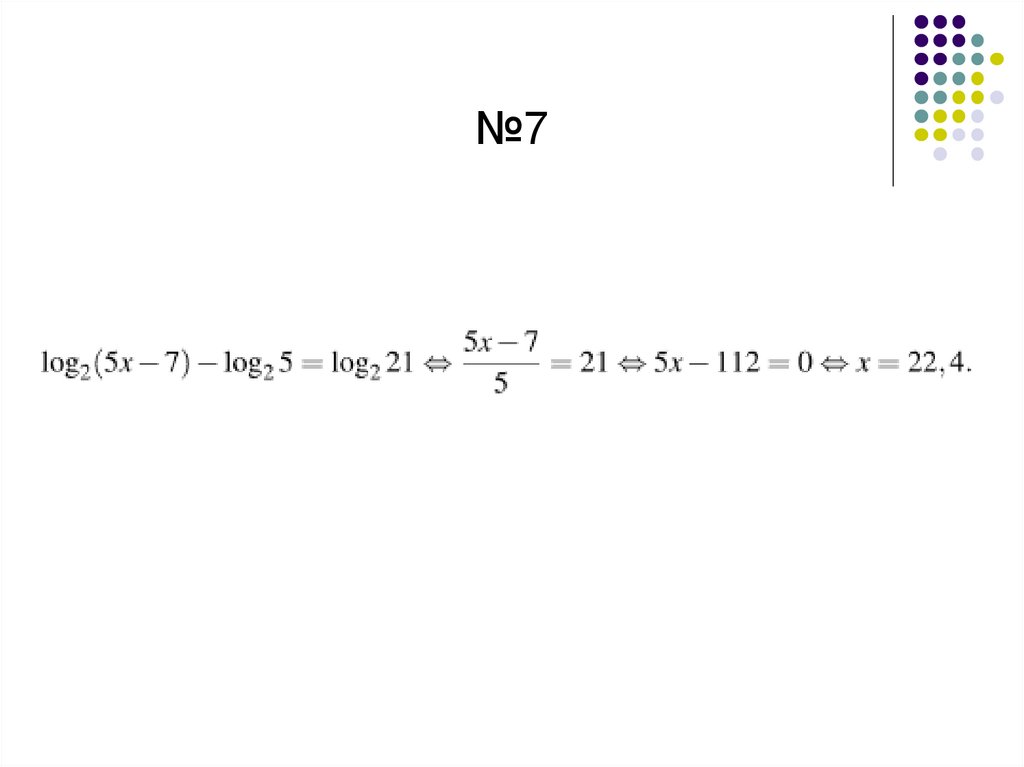

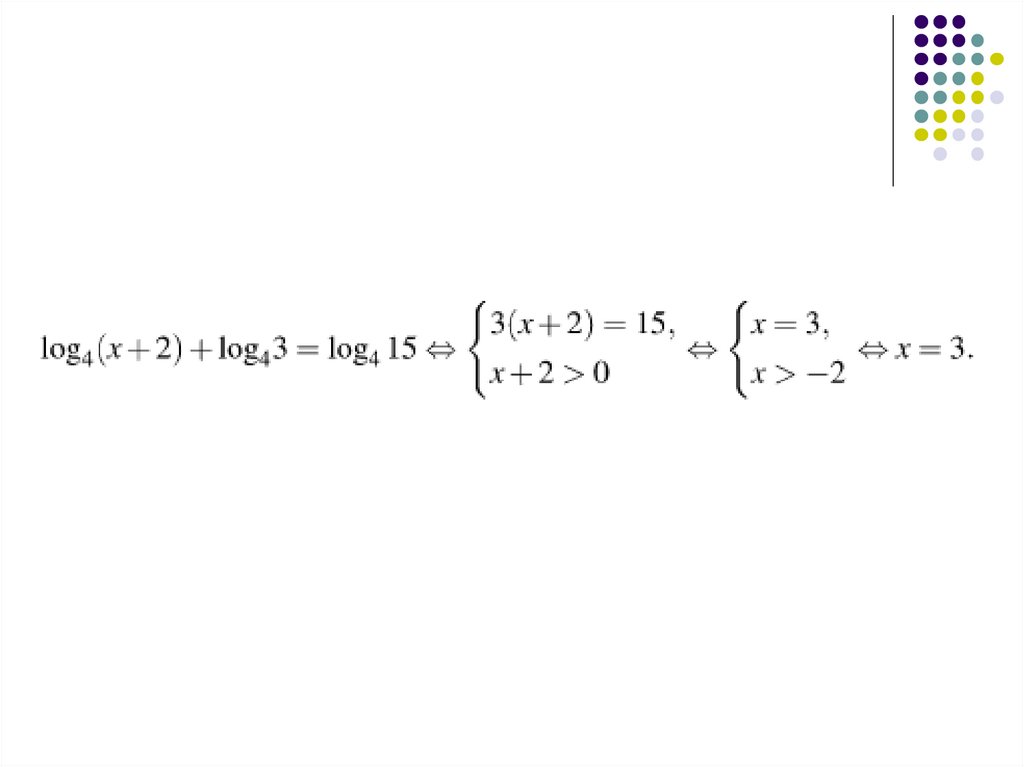


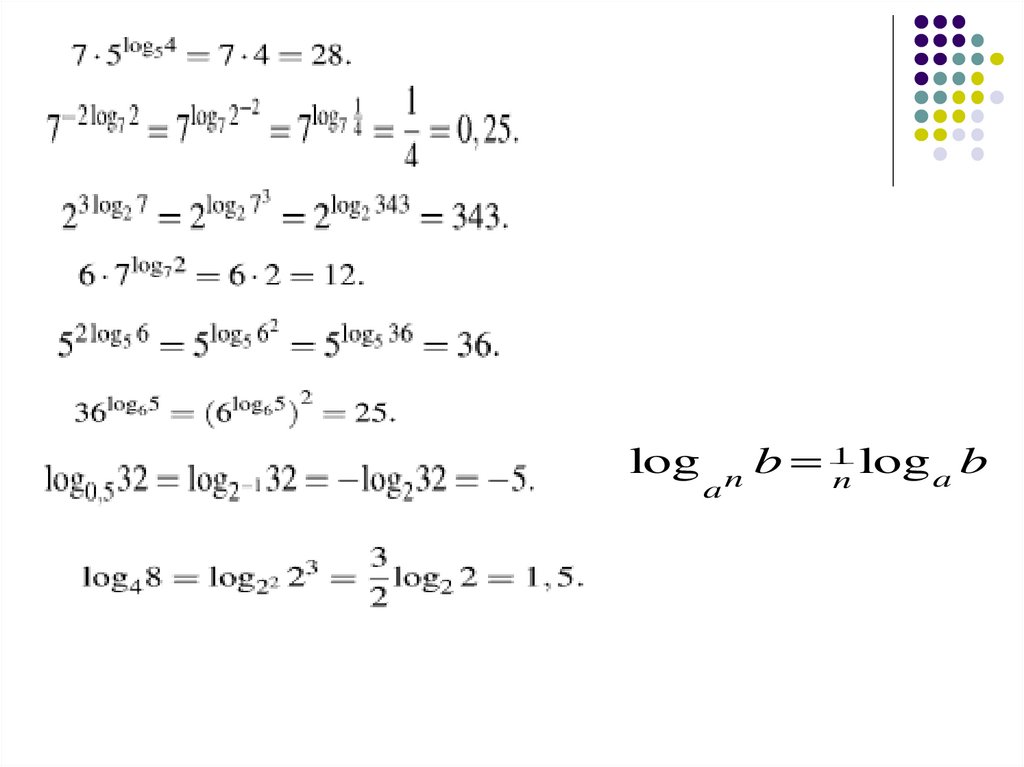
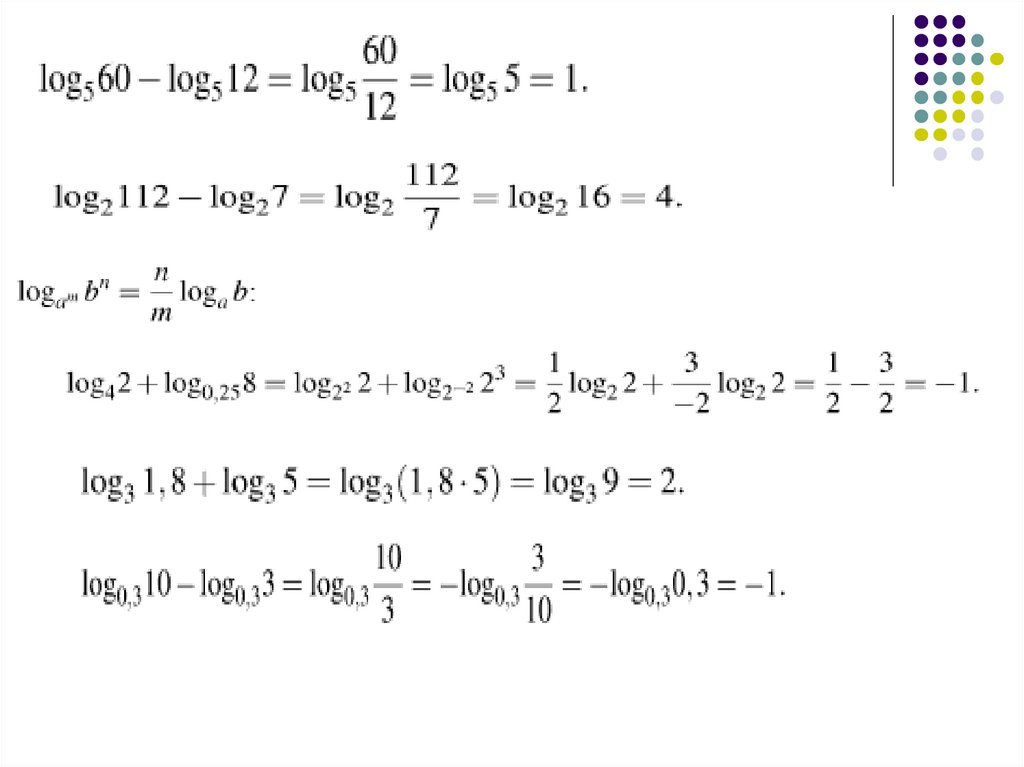

 Математика
Математика








