Похожие презентации:
Электромагнитные переходные процессы при нарушении симметрии трехфазной цепи
1.
2.
Метод симметричных составляющихЛюбой из векторов симметричной трехфазной
системы можно представить одноименным
вектором другой фазы с помощью оператора
поворота
a e
j 120
1
3
j
2
2
Умножение вектора на оператор a означает
поворот его на 120° в положительном направлении
(против часовой стрелки).
2
3.
a ea e
2
j 120
j 240
1
3
j
2
2
e
j 120
Сумма операторов поворота
Разность операторов поворота
a e
3
j 360
1
3
j
2
2
a a 1
2
a a j 3
2
1 a
3n m
a
m
3
4.
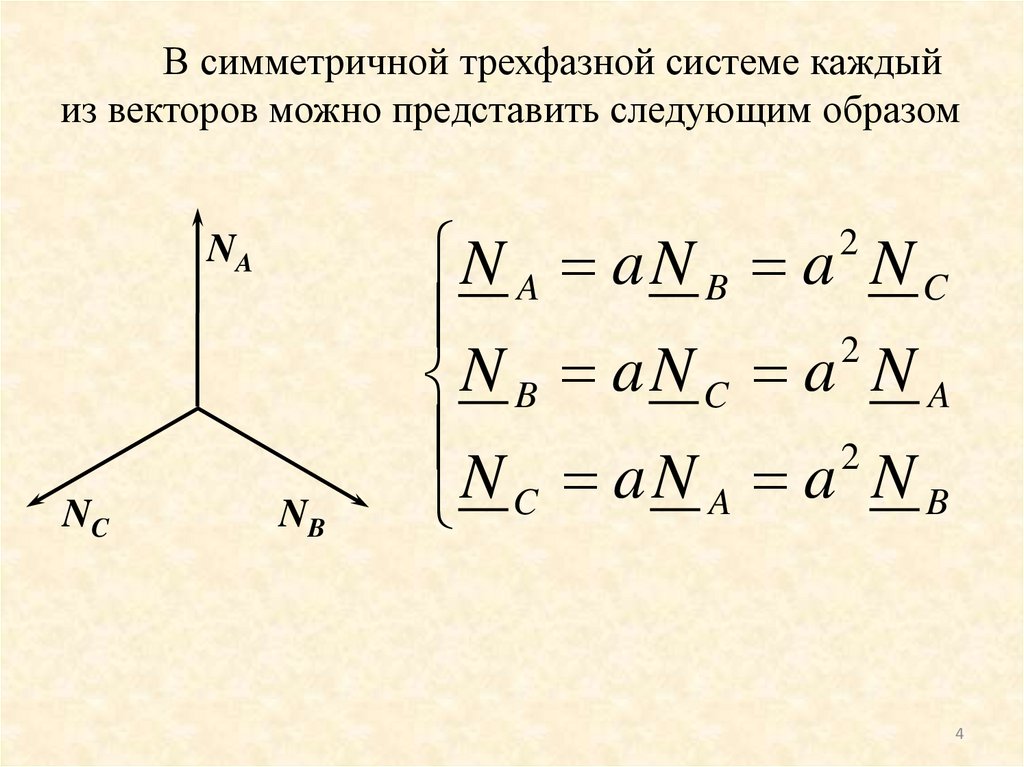
В симметричной трехфазной системе каждыйиз векторов можно представить следующим образом
NC
N A a N B a N C
2
N B a N C a N A
2
N
a
N
a
N
C
A
B
2
NA
NB
4
5.
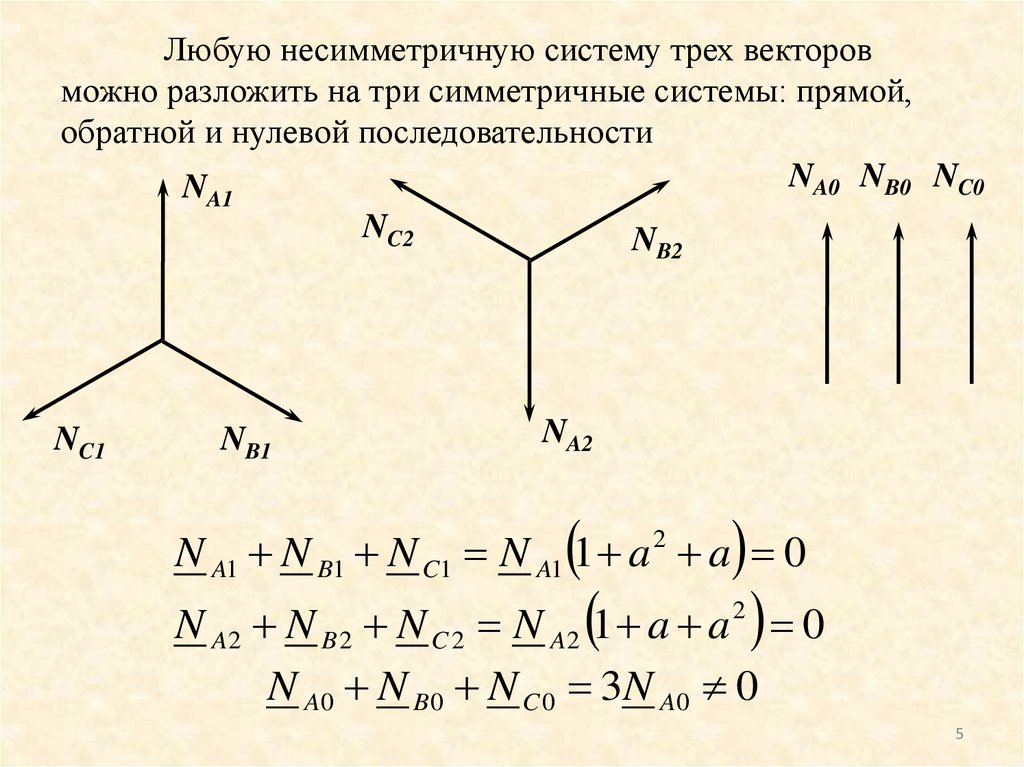
Любую несимметричную систему трех векторовможно разложить на три симметричные системы: прямой,
обратной и нулевой последовательности
NA0 NB0 NC0
NA1
NC2
N
B2
NC1
NB1
NA2
N A1 N B1 N C1 N A1 1 a 2 a 0
N A2 N B 2 N C 2 N A2 1 a a 0
N A0 N B 0 N C 0 3 N A0 0
2
5
6.
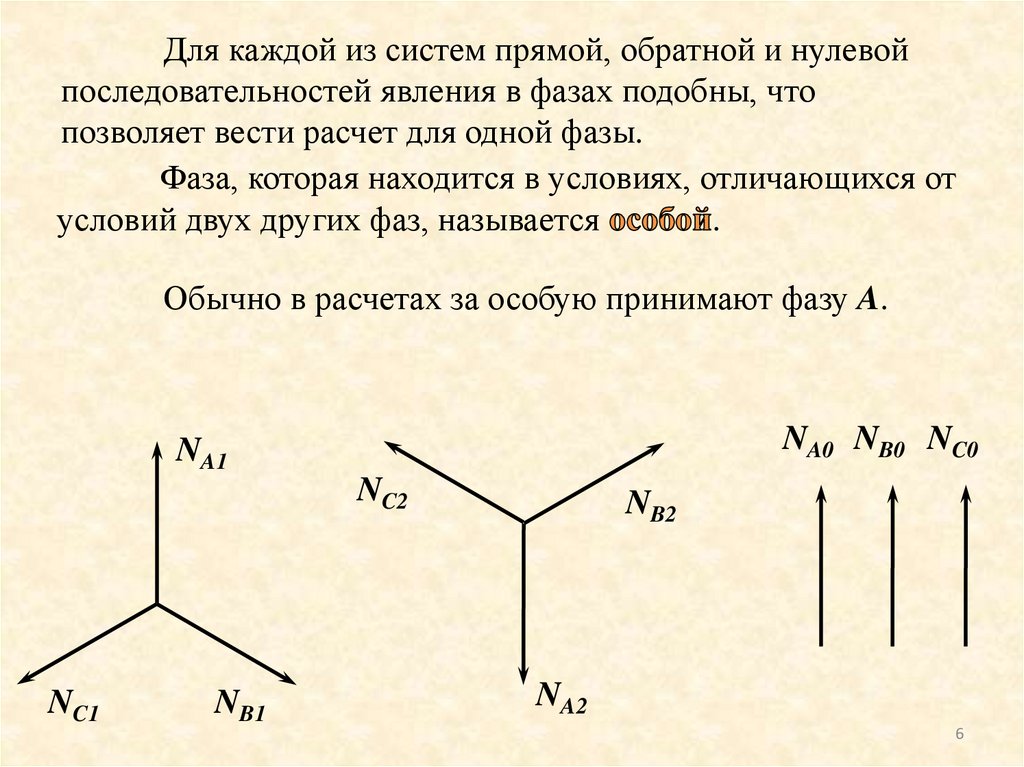
Для каждой из систем прямой, обратной и нулевойпоследовательностей явления в фазах подобны, что
позволяет вести расчет для одной фазы.
Фаза, которая находится в условиях, отличающихся от
условий двух других фаз, называется
.
Обычно в расчетах за особую принимают фазу A.
NA0 NB0 NC0
NA1
NC2
NC1
NB1
NB2
NA2
6
7.
По составляющим прямой, обратной и нулевойпоследовательности можно восстановить исходную
несимметричную систему.
N A N A1 N A 2 N A0
N B N B1 N B 2 N B 0
N N N N
C1
C2
C0
C
Если принять за особую фазу A, то систему можно записать
N A N A1 N A 2 N A0
2
N B a N A1 a N A 2 N A0
2
N
a
N
a
N A 2 N A0
A1
C
7
8.
Составляющие прямой, обратной и нулевойпоследовательности через векторы фазных величин
N
3
N A1 N A a N B a N C 3
N A2
2
a N B aN C
2
A
N A0 N A N B N C 3
8
9.
Допущения при расчете несимметричных режимов:1) в симметричных цепях токи и напряжения
различных последовательностей не взаимодействуют друг с
другом
2) каждый элемент цепи оказывает свое сопротивление
токам различных последовательностей
3) симметричные составляющие токов связаны
симметричными составляющими напряжений только
одноименной последовательности
U1 Z1 I1
U 2 Z 2 I 2
U 0 Z 0 I 0
где Z1, Z2, Z0 – сопротивления прямой, обратной и
нулевой последовательностей.
9
10.
Схемы замещения отдельныхпоследовательностей
Полностью соответствует схеме, составляемой
для расчета трехфазного КЗ.
В зависимости от применяемого метода расчета и
момента времени генераторы и нагрузки вводятся в нее
ЭДС и соответствующими реактивностями. Все
остальные элементы вводят в схему неизменными во
времени сопротивлениями.
10
11.
.По структуре аналогична схеме прямой последовательности,
но ЭДС всех генерирующих элементов в ней приравниваются нулю,
а сопротивления обратной последовательности считают
постоянными для любого момента времени.
Если точные значения сопротивлений обратной
последовательности для электрических машин неизвестны, то
принимают:
- для машин без демпферных обмоток X2≈1,45 X'd
- для турбогенераторов и машин с демпферной обмоткой
X2≈1,22 X''d.
В практических расчетах часто принимают X2≈X''d
Параметры остальных элементов в схеме обратной
последовательности соответствуют их величинам в схеме
прямой последовательности.
11
12.
1213.
Сопротивление элементов нулевой последовательности:а) Синхронные машины
X0≈(0,15÷0,16) X''d
Как правило схемы соединения обмоток трансформаторов и
подключаемых к ним генераторов подбирают Y, Δ, чтобы
исключить протекание через генераторы токов нулевой
последовательности.
б) Обобщенная нагрузка
X0 - определяется сопротивлениями и схемами соединения
входящих в нее элементов и питающих обмоток
трансформаторов.
Как правило понижающие обмотки питающих
трансформаторов соединяются в Δ, что исключает
проникновение в нагрузку токов нулевой последовательности.
в) Токоограничивающие реакторы
X0=X2=X1
13
14.
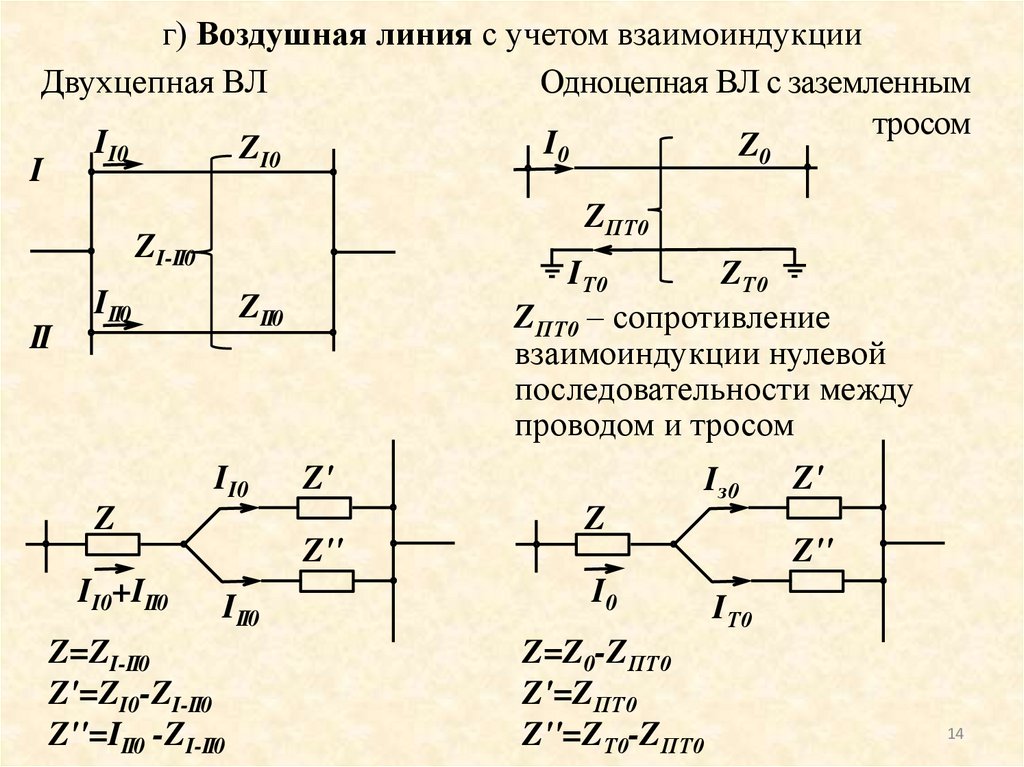
г) Воздушная линия с учетом взаимоиндукцииДвухцепная ВЛ
Одноцепная ВЛ с заземленным
тросом
II0
I0
Z0
ZI0
I
ZПТ0
ZI-II0
IТ0
ZТ0
III0
ZII0
ZПТ0 – сопротивление
II
взаимоиндукции нулевой
последовательности между
проводом и тросом
II0
Z'
Z
Iз0
Z
Z''
II0+III0
Z'
III0
Z=ZI-II0
Z'=ZI0-ZI-II0
Z''=III0 -ZI-II0
Z''
I0
Z=Z0-ZПТ0
Z'=ZПТ0
Z''=ZТ0-ZПТ0
IТ0
14
15.
Воздушные линии- одноцепные без тросов
- одноцепные со стальными тросами
- двухцепные без тросов
- двухцепные со стальными тросами
X0=3,5X1
X0=3,0X1
X0=5,5X1
X0=4,7X1
д) Кабельные линии
X0≈(3,5÷4,6) X1
r0≈10r1
15
16.
е) Трансформаторы и автотрансформаторыВеличина X0 определяется их конструкцией и
соединением обмоток
Сопротивление нулевой последовательности
трансформаторов со стороны обмотки, соединенной в Δ или Y
равно X0=∞.
Сопротивление нулевой последовательности
трансформаторов со стороны обмотки, соединенной Y-0 зависит
от схемы соединения других обмоток и наличия в их цепи
контуров для прохождения токов нулевой последовательности.
16
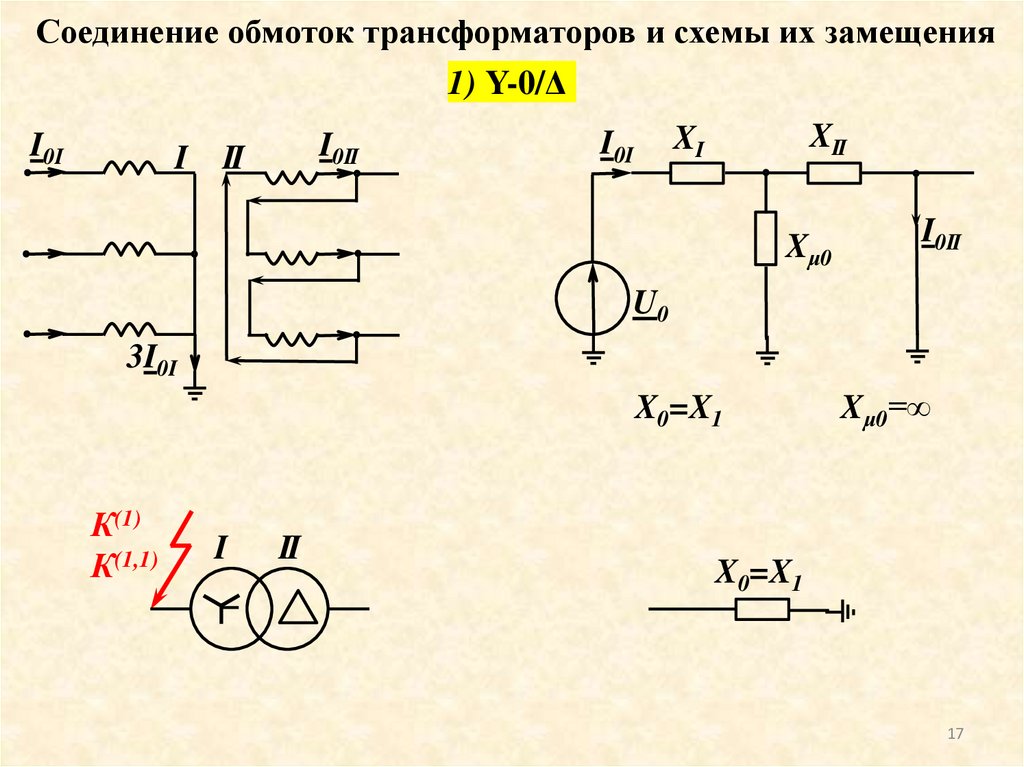
17. Соединение обмоток трансформаторов и схемы их замещения
1) Y-0/ΔI0I
I
I0II
II
XII
XI
I0I
Xμ0
I0II
U0
3I0I
X0=X1
К(1)
К(1,1)
I
II
Xμ0=∞
X0=X1
17
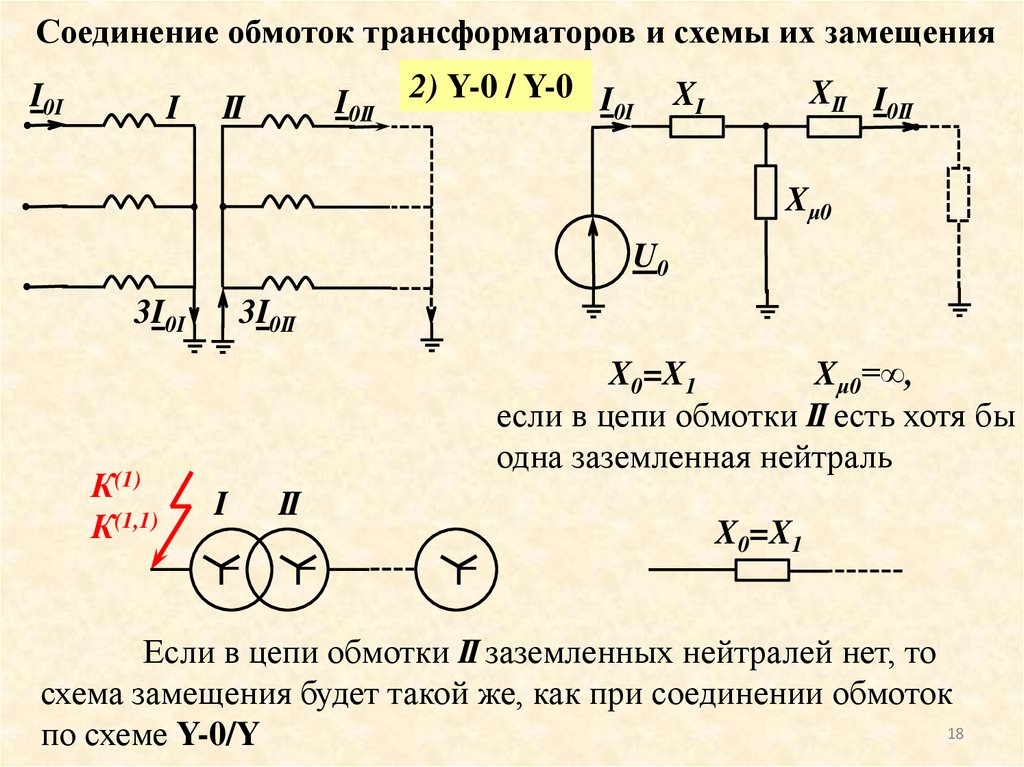
18. Соединение обмоток трансформаторов и схемы их замещения
I0II
I0II
II
2) Y-0 / Y-0 I
0I
XII I0II
XI
Xμ0
U0
3I0I
К(1)
К(1,1)
3I0II
X0=X1
Xμ0=∞,
если в цепи обмотки II есть хотя бы
одна заземленная нейтраль
I
II
X0=X1
Если в цепи обмотки II заземленных нейтралей нет, то
схема замещения будет такой же, как при соединении обмоток
18
по схеме Y-0/Y
19. Соединение обмоток трансформаторов и схемы их замещения
3) Y-0/YI0I
I
II
I0I
XI
XII
Xμ0
U0
3I0I
X0=XI+Xμ0
XI=XII=X1/2
Для группы и трех однофазных трансформаторов и для
трехфазных трансформаторов с четырьмя и пятью
магнитопроводами
Xμ0=∞
Сопротивление намагничивания трехфазных
трехстержневых трансформаторов
X*μ0=0,3÷1
19
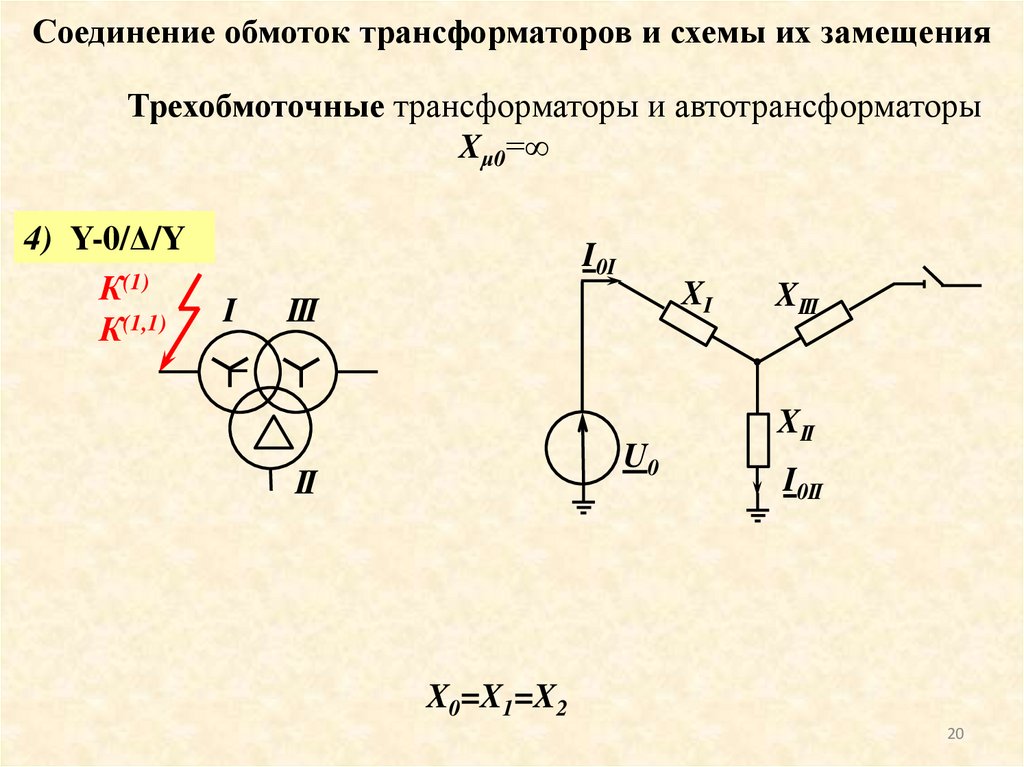
20. Соединение обмоток трансформаторов и схемы их замещения
Трехобмоточные трансформаторы и автотрансформаторыXμ0=∞
4) Y-0/Δ/Y
К(1)
К(1,1)
I0I
I
XI
III
U0
II
XIII
XII
I0II
X0=X1=X2
20
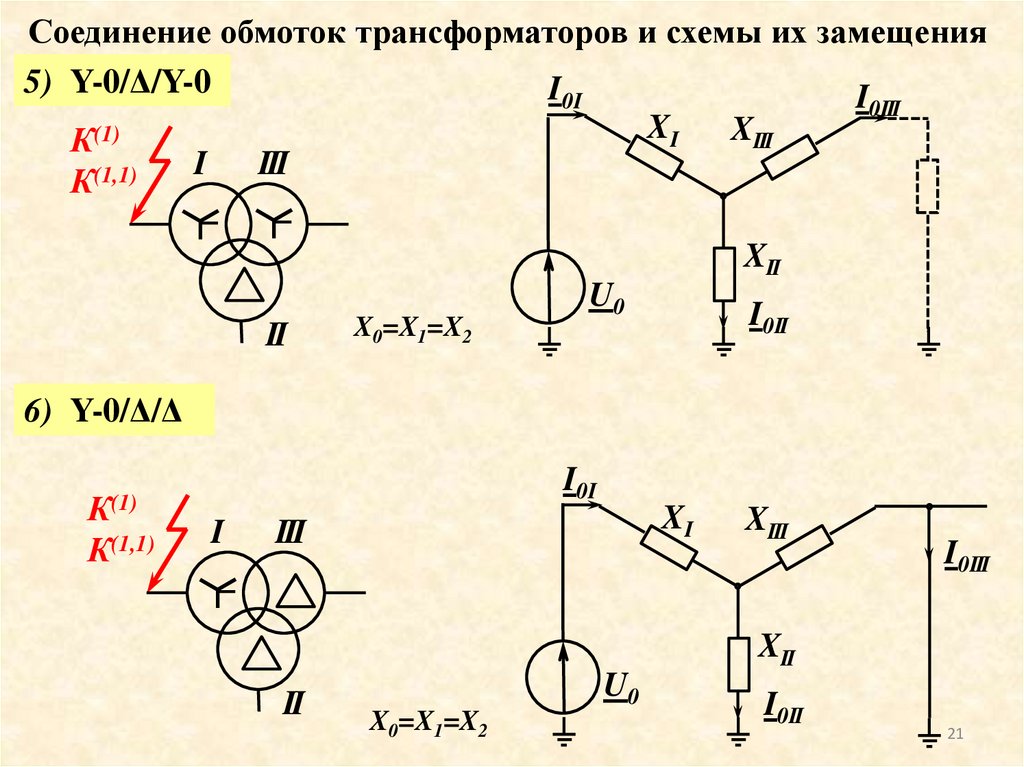
21. Соединение обмоток трансформаторов и схемы их замещения
5) Y-0/Δ/Y-0I0I
I0III
XI
XIII
К(1)
I III
(1,1)
К
XII
II
X0=X1=X2
U0
I0II
6) Y-0/Δ/Δ
К(1)
К(1,1)
I0I
I
XI
III
XIII
I0III
XII
II
U0
X0=X1=X2
I0II
21
22. Соединение обмоток трансформаторов и схемы их замещения
Если в нейтраль обмотки трансформатора, по которойпротекает ток нулевой последовательности, включено
сопротивление, то оно учитывается последовательным
включением в схему замещения сопротивления утроенной
величины
К(1)
К(1,1)
I
II
XТ0
3Z
Z
22
23.
2324.
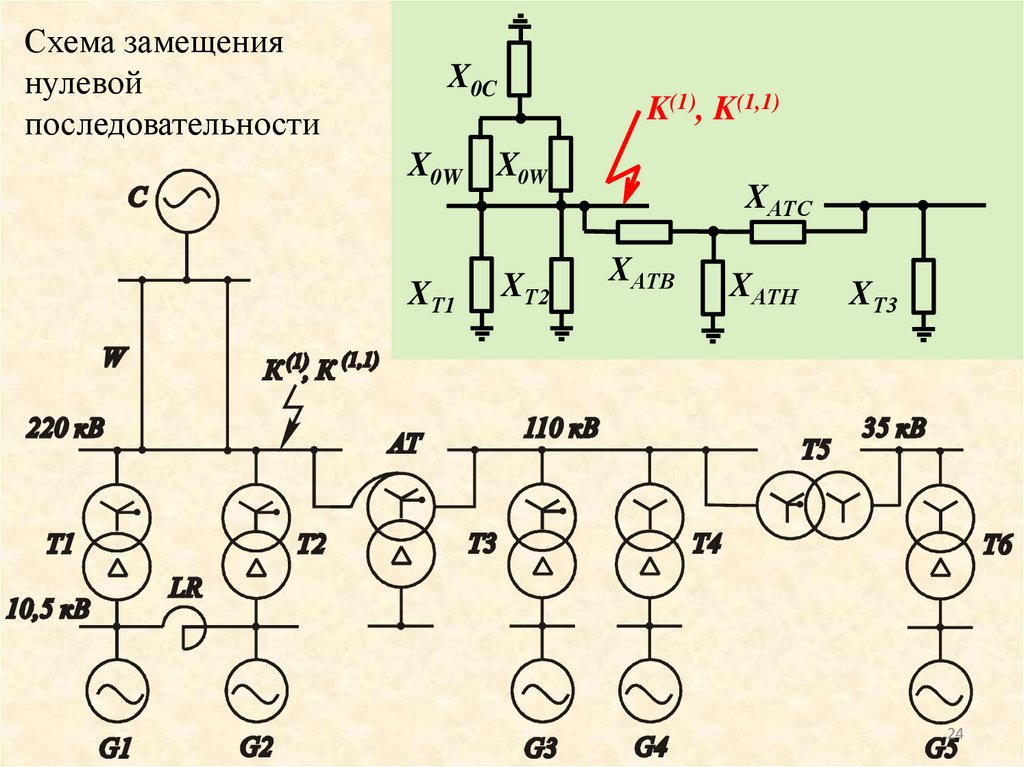
Схема замещениянулевой
последовательности
X0C
K(1), K(1,1)
X0W X0W
XТ1
XТ2
XАТС
XАТВ
XАТН
XТ3
24
25.
2526.
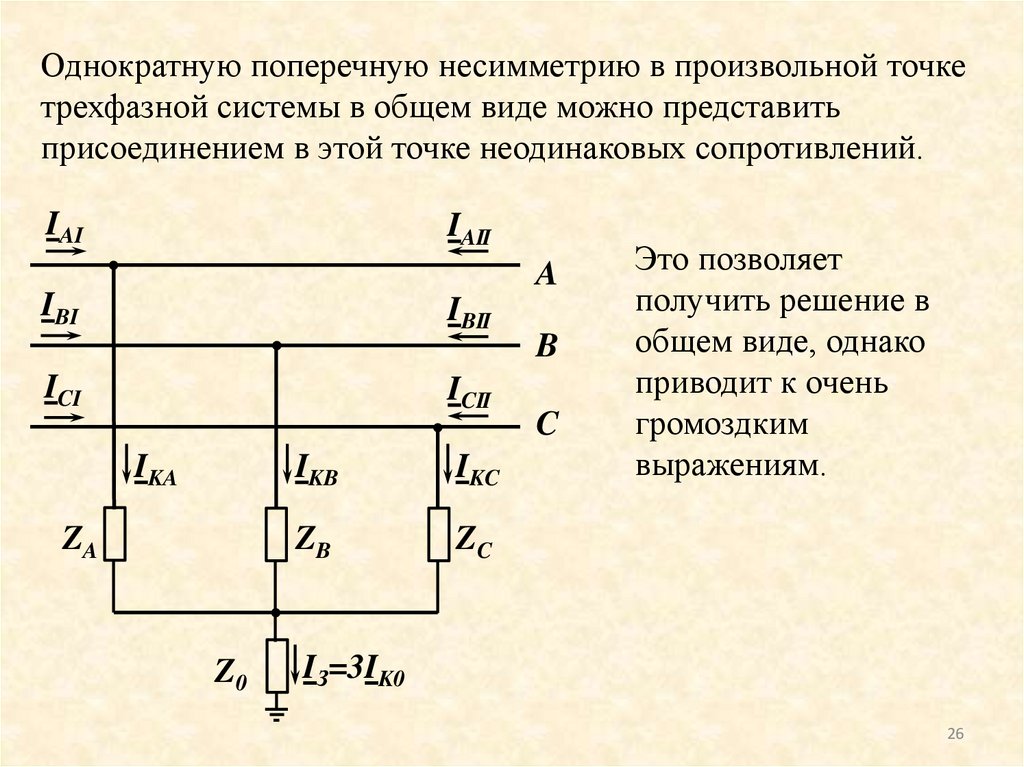
Однократную поперечную несимметрию в произвольной точкетрехфазной системы в общем виде можно представить
присоединением в этой точке неодинаковых сопротивлений.
IAI
IAII
A
IBI
IBII
ICI
ICII
IKA
ZA
Z0
IKB
IKC
ZB
ZC
B
C
Это позволяет
получить решение в
общем виде, однако
приводит к очень
громоздким
выражениям.
IЗ=3IK0
26
27.
Значительно проще решать задачу для каждого вида КЗ,используя его граничные условия.
Допущения:
1. Фаза A является особой фазой.
2. Все сопротивления реактивные.
3. Положительное направление токов – к месту КЗ.
27
28.
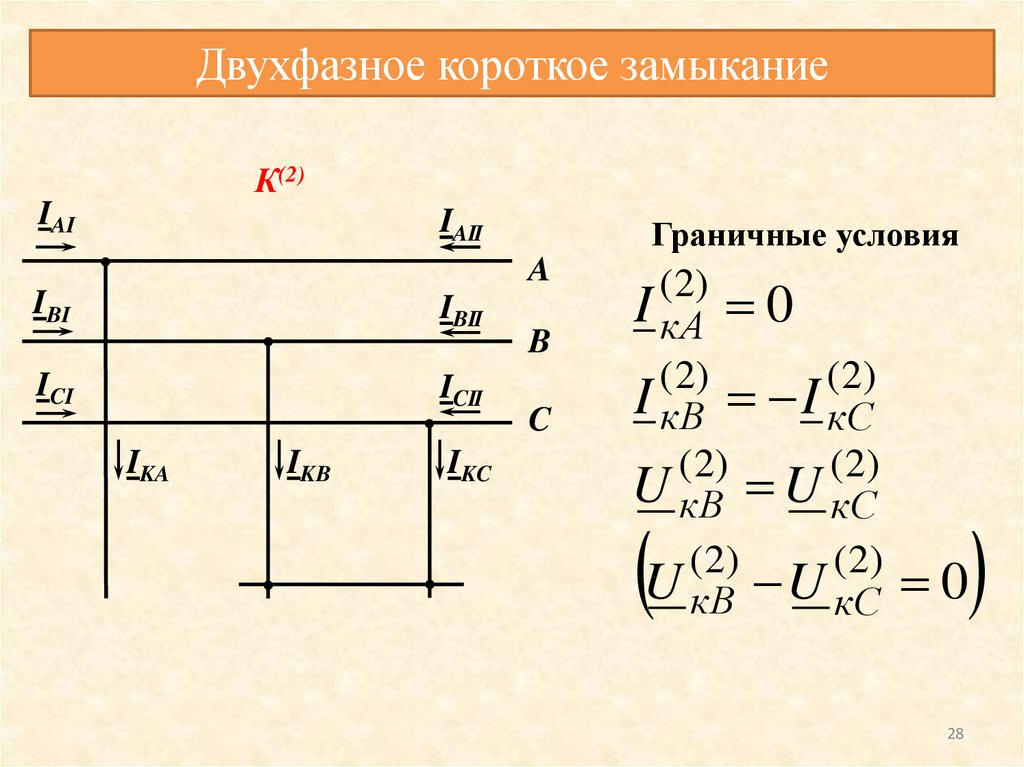
Двухфазное короткое замыканиеК(2)
IAI
IAII
Граничные условия
A
IBI
IBII
ICI
ICII
IKA
IKB
IKC
B
C
( 2)
I кA 0
( 2)
( 2)
I кB I кC
( 2)
( 2)
U кB U кC
( 2)
( 2)
U кB U кC
0
28
29.
Выразим все токи и напряжения через IкA1 так, чтобысоблюдались граничные условия
Поскольку система токов уравновешенная, то есть
I A I B I C 0, то I к 0 0
I кA I кA1 I кA2 0, I кA2 I кA1
тогда
Токи поврежденных фаз в месте КЗ
( 2)
I кB
( 2)
( 2)
I кB1 I кB2
a a
2
( 2)
I кA1
( 2)
I кAC
( 2)
2 ( 2)
a I кA1 a I кA2
j
j
( 2)
3 I кA1
( 2)
3 I кA1
29
30.
Выразим UкB и UкC через симметричные составляющие фазы A( 2)
U кB
( 2)
U кC
0
U кB1 U кB 2 U кB 0 U кC1 U кC 2 U кC 0 0
a 2U кA1 aU кA2 U кA0 aU кA1 a 2U кA2 U кA0
a
a 0
a 2 a U кA1 U кA2 0
2
U кA2 U кA1
30
31.
Напряжение прямой и обратной последовательностей фазы A вместе КЗ
( 2)
U кA1
( 2)
U кA2
( 2)
jX 2 I кA2
( 2)
jX 2 I кA1
Напряжение нулевой последовательности
( 2)
U к0
( 2)
jX 0 I к 0
0
(неопределенность)
Фазные напряжения
( 2)
U кA
( 2)
U кB
( 2)
( 2)
U кA1 U кA2
( 2)
U кC
a
2
( 2)
2U кA1
( 2)
( 2)
U кA1 aU кA2
( 2)
2 jX 2 I кA1
( 2)
U кA1
( 2)
U кA
2
31
32.
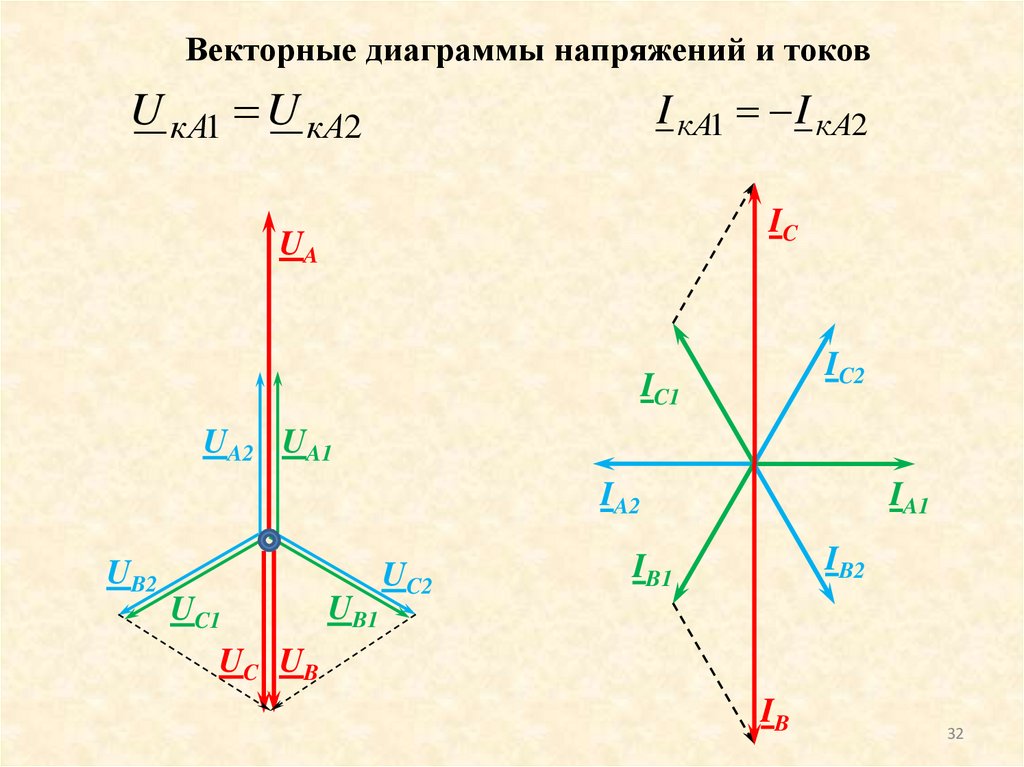
Векторные диаграммы напряжений и токовU кA1 U кA2
I кA1 I кA2
IC
UA
IC2
IC1
UA2 UA1
IA2
UB2
UC1
UB1
UC2
IA1
IB2
IB1
UC UB
IB
32
33.
Однофазное короткое замыканиеIAI
К(1)
Граничные условия
IAII
A
IBI
IBII
ICI
ICII
IKA
IKB
(1)
I кB 0
(1)
I кC 0
(1)
U кA 0
B
C
IKC
I
(1)
кA1
I
(1)
кA 2
I
(1)
к0
1 (1)
I кA
3
Ток в поврежденной фазе в месте КЗ
I
(1)
кA
3I
(1)
кA1
33
34.
Для поврежденной фазы имеемU кA U кA1 U кA2 U кA0 0
Симметрические составляющие напряжений в месте КЗ
U к 0 jX 0 I к 0 jX 0 I кA1
U кA2 jX 2 I кA2 jX 2 I кA1
U кA1 U кA2 U кA0 j X 2 X 0 I кA1
Фазные напряжения в месте КЗ
(1)
U кB
a
2
(1)
(1)
U кA1 aU кA2
(1)
U к0
j a a X 2 a 1
2
2
(1)
X 0 I кA1
1)
1)
U (кC
j a a 2 X 2 a 1 X 0 I (кA
1
34
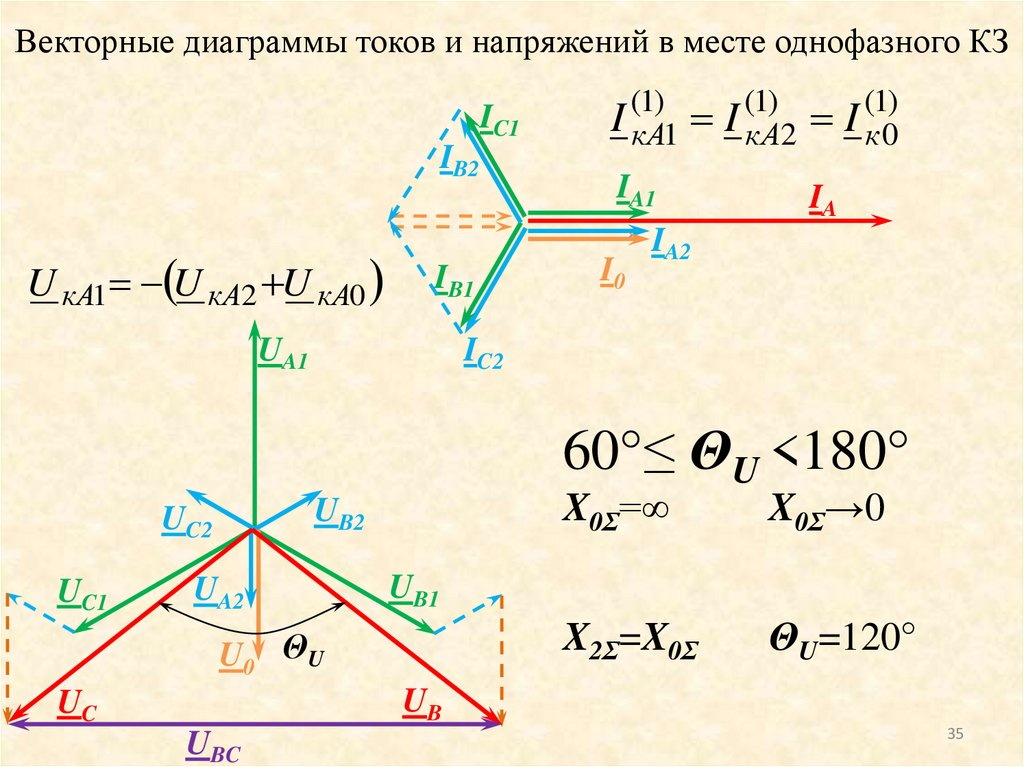
35.
Векторные диаграммы токов и напряжений в месте однофазного КЗIC1
IB2
U кA1 U кA2 U кA0
IB1
UA1
(1)
I кA1
IA1
I0
(1)
I кA2
(1)
I к0
IA
IA2
IC2
60°≤ ΘU <180°
UB2
UC2
UC1
UA2
X0Σ=∞
X0Σ→0
X2Σ=X0Σ
ΘU=120°
UB1
U0 ΘU
UB
UC
UBC
35
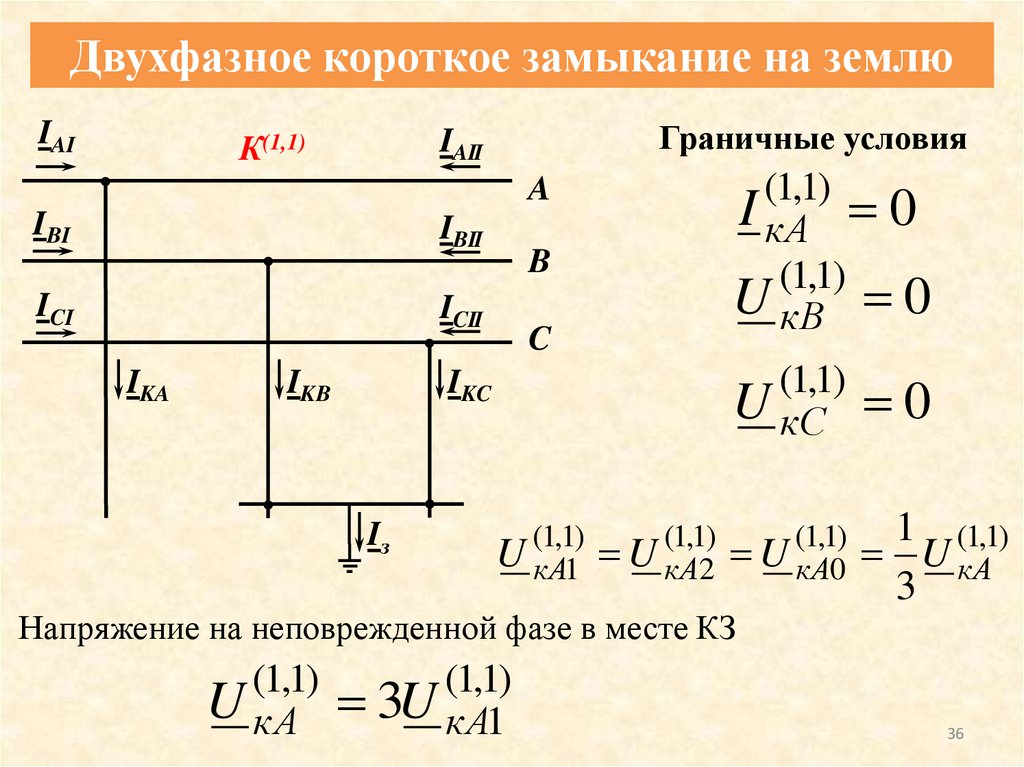
36.
Двухфазное короткое замыкание на землюIAI
Граничные условия
IAII
К(1,1)
(1,1)
I кA 0
(1,1)
U кB 0
A
IBI
IBII
ICI
B
ICII
IKA
IKB
C
IKC
Iз
(1,1)
U кA1
(1,1)
U кA2
(1,1)
U кC
0
(1,1)
U кA0
1 (1,1)
U кA
3
Напряжение на неповрежденной фазе в месте КЗ
(1,1)
U кA
(1,1)
3U кA1
36
37.
(1,1)I кA1
(1,1)
I кA2
(1,1)
U кA2
(1,1)
U кA0
(1,1)
I кA
(1,1)
U кA1
(1,1)
I кA2
jX 2
(1,1)
I к0
0 (*)
1 (1,1)
U кA ,
3
(1,1)
I к0
тогда
jX 0
Прибавив к обеим частям равенства IК0 jX2∑ и учтя (*), после
преобразований получим:
X 0
X 2
(1,1)
(1,1)
(1,1)
(1,1)
I кA2 I кA1
I к 0 I кA1
X 2 X 0
X 2 X 0
(1,1)
U кA1
(1,1)
I кA1
X 2 X 0
j
X 2 X 0
37
38.
Токи поврежденных фаз в месте КЗ(1,1)
I кB
(1,1)
I кC
2 X 2 aX 0 (1,1)
I кA1
a
X 2 X 0
2
(1,1)
X
a
X
2
0
I кA1
a
X
X
2
0
Модули выражений в скобках
X 2 X 0
Ток в земле
1,5 m
m
(1,1)
(1,1)
X 2 X 0
3 1
2
X 2 X 0
3
X 0
1,1
1,1
I
3I
з
к0
38
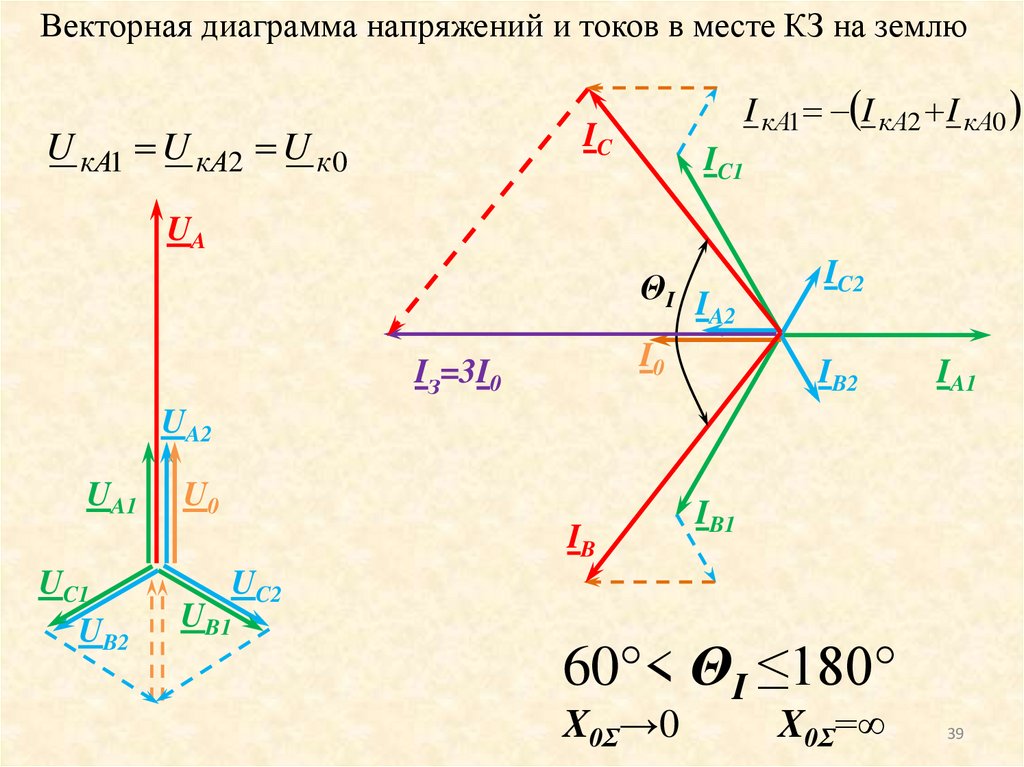
39.
Векторная диаграмма напряжений и токов в месте КЗ на землюU кA1 U кA2 U к 0
I кA1 I кA2 I кA0
IC
IC1
UA
Iз=3I0
ΘI I
A2
IC2
I0
IB2
IA1
UA2
UA1
U0
IB
UC1
UB2
IB1
UC2
UB1
60°< ΘI ≤180°
X0Σ→0
X0Σ=∞
39
40.
Правило эквивалентности прямойпоследовательности
40
41.
E1ΣX1Σ
XΔ
UkA1
K(3)
Uk=0
IKA1
Ток прямой последовательности фазы A при любом несимметричном КЗ
( n)
I кA1
E1
jX1
jX ( n)
,
где XΔ(n) – дополнительное сопротивление, зависящее от вида КЗ
X (1) X 2 X 0
( 2)
X
X 2
(1,1)
X
X 2 X 0
X 2 X 0
41
42.
Фазные токи в месте КЗ пропорциональны току прямойпоследовательности
( n)
Iк
( n)
I П0
m
( n)
( n)
I кA1,
где m(n) – коэффициент, зависящий от вида КЗ.
m
(1)
3
m
( 2)
3
m
(1,1)
X 2 X 0
3 1
2
X 2 X 0
42
43.
E1ΣX1Σ
UkA1
XΔ
K(3)
Uk=0
IKA1
( n)
U к1
( n) ( n)
jX I к1 ,
Идентичность между током прямой
последовательности несимметричного КЗ и током при
эквивалентном трехфазном КЗ позволяет использовать
все выражения для расчета тока трехфазного КЗ при
расчете несимметричных КЗ.
43


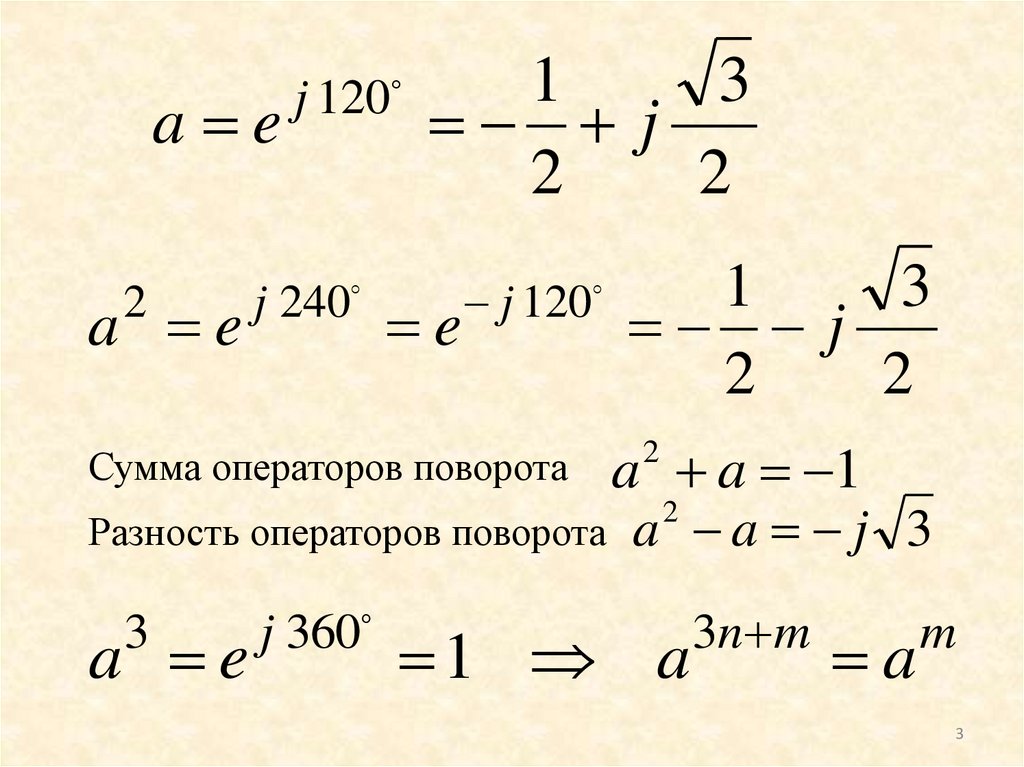














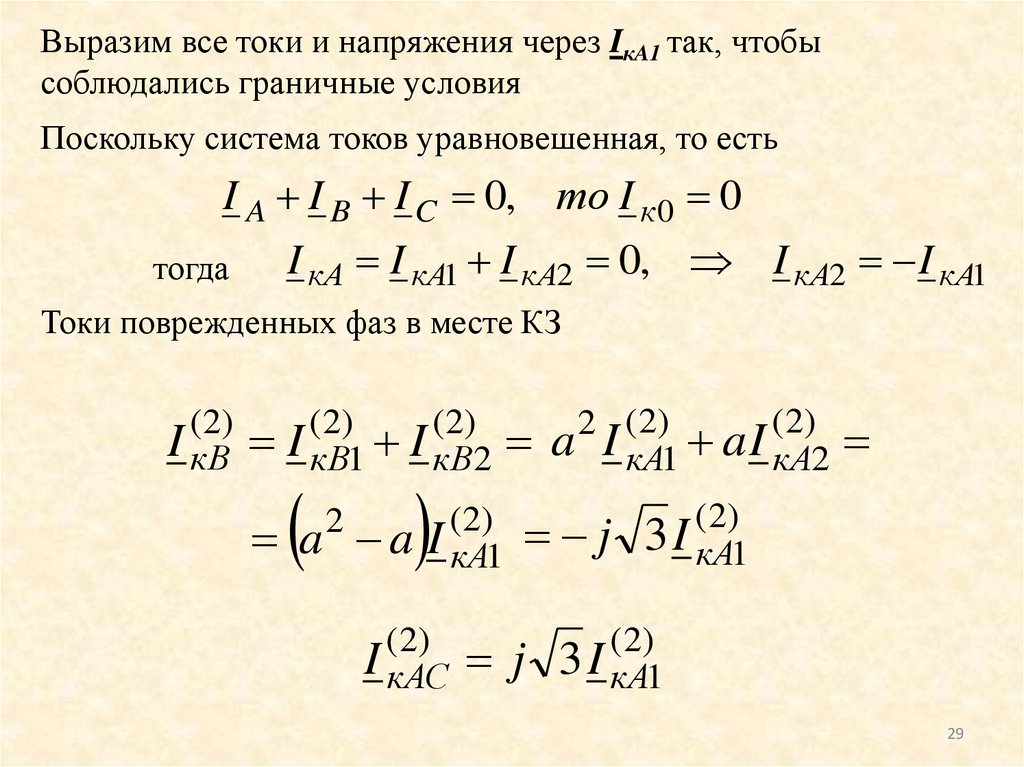




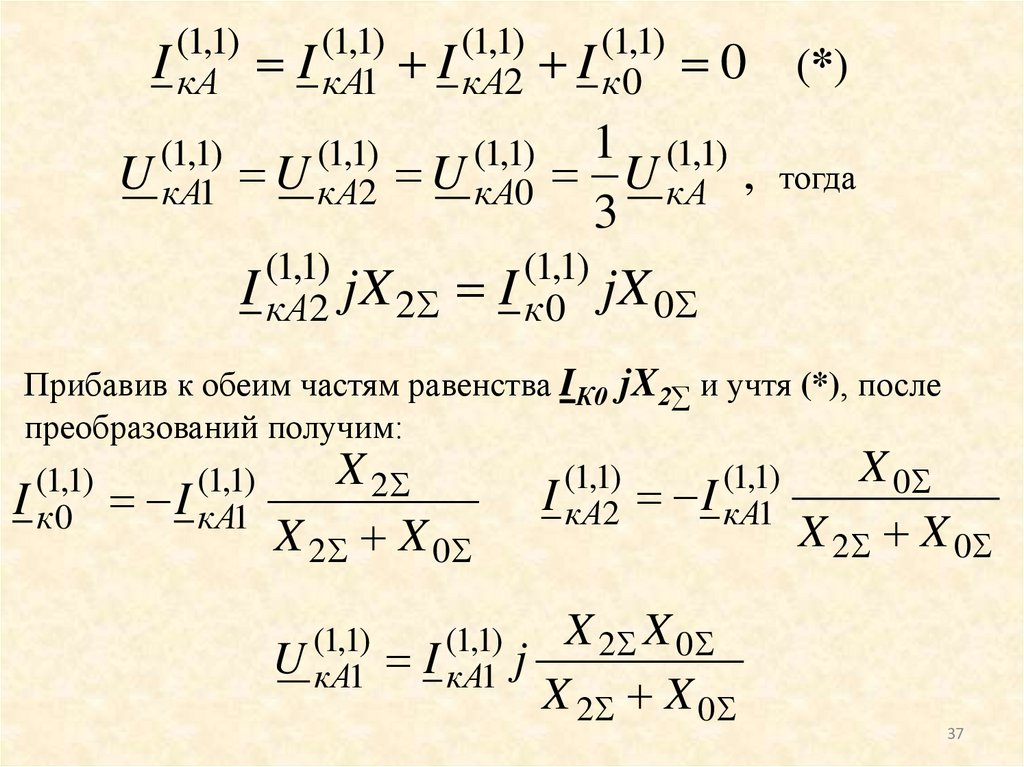





 Электроника
Электроника








