Похожие презентации:
Определение расстояний в астрономии
1.
2.
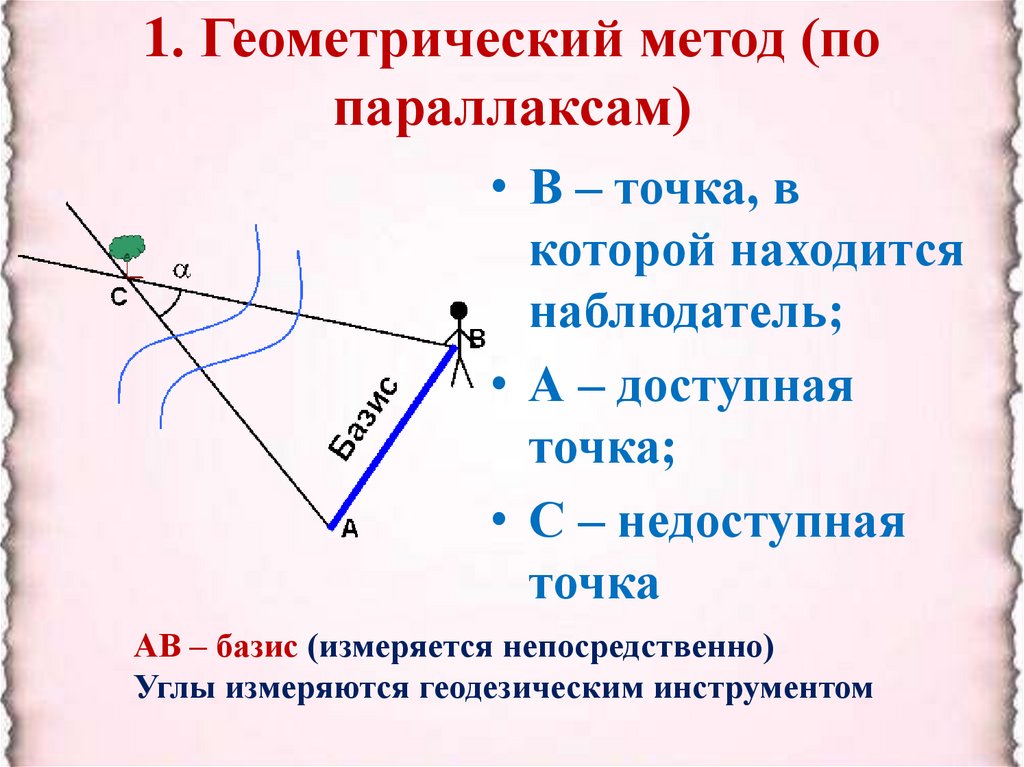
1. Геометрический метод (попараллаксам)
• В – точка, в
которой находится
наблюдатель;
• А – доступная
точка;
• С – недоступная
точка
АВ – базис (измеряется непосредственно)
Углы измеряются геодезическим инструментом
3.
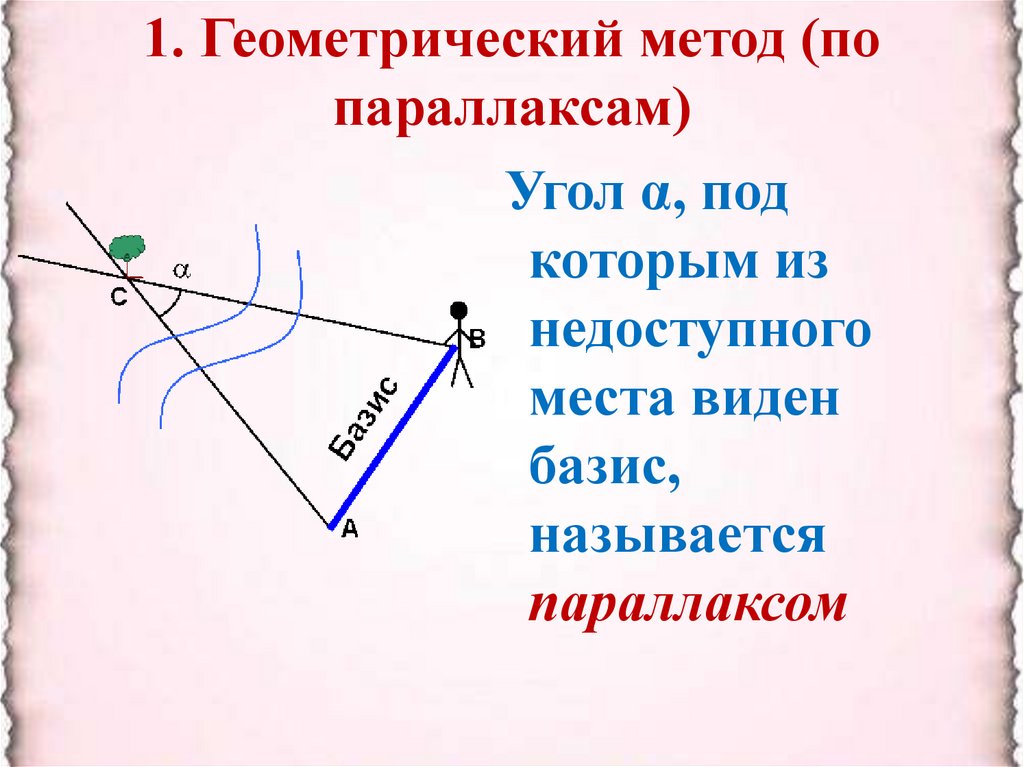
1. Геометрический метод (попараллаксам)
Угол α, под
которым из
недоступного
места виден
базис,
называется
параллаксом
4.
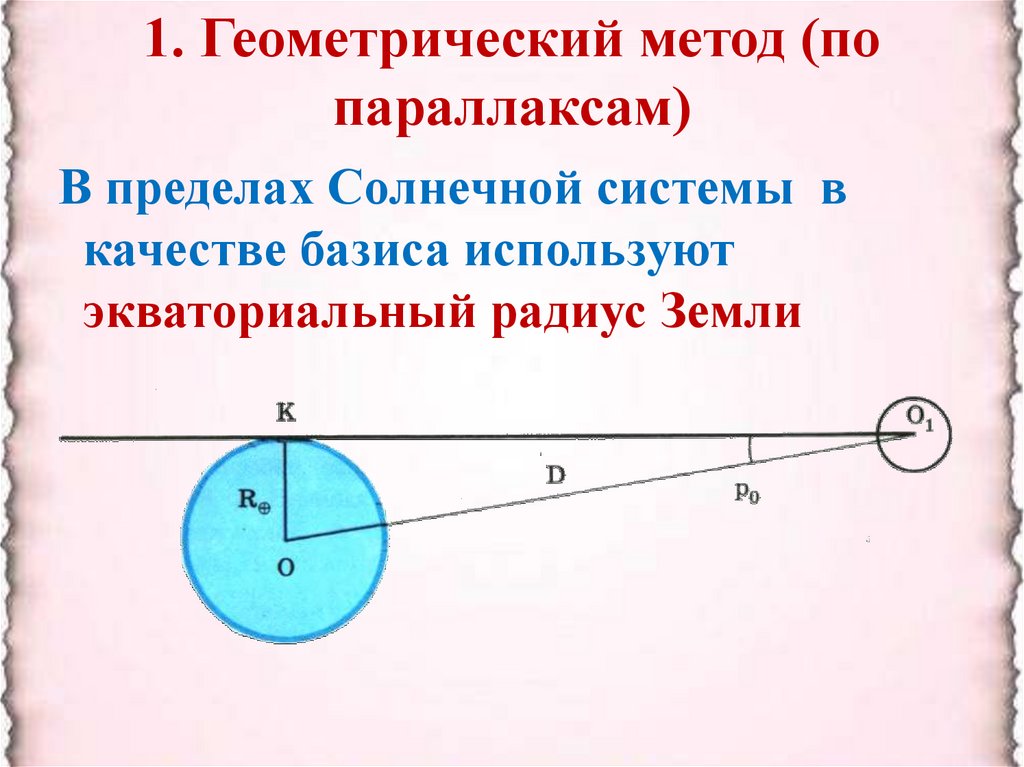
1. Геометрический метод (попараллаксам)
В пределах Солнечной системы в
качестве базиса используют
экваториальный радиус Земли
5.
1. Геометрический метод (попараллаксам)
Угол р0 , под которым со светила,
находящегося на горизонте, был бы
виден экваториальный радиус Земли,
называется горизонтальным
экваториальным параллаксом светила
6.
1. Геометрический метод (попараллаксам)
Если горизонтальный параллакс
найден, то расстояние до светила
вычисляется по формуле:
R
D
sin p0
где D – расстояние от центра Земли до центра
какого либо тела Солнечной системы;
R ‒ экваториальный радиус Земли
7.
1. Геометрический метод (попараллаксам)
Поскольку углы р0 очень малы, то их
синусы можно заменить самими углами,
если величина угла выражена в
радианах: sin p0 p0
но обычно р0 выражено в секундах дуги,
поэтому:
p0
sin p0
206265
8.
1. Геометрический метод (попараллаксам)
Тогда:
206265
D
R
p0
Параллакс выражен в секундах дуги,
а D – либо в километрах, либо в
радиусах Земли
9.
2. Радиолокационный методРадиолокация
заключается в том,
что на небесное тело
посылают мощный
кратковременный
радиоимпульс, а
потом принимают
отраженный сигнал
10.
2. Радиолокационный методc t
D
2
Зная скорость света
в вакууме:
с = 299 792 458 м/с
и точно измерив
время
прохождения
сигнала туда и
обратно, легко
вычислить
расстояние до
небесного тела
11.
2. Радиолокационный методРадиолокационные
наблюдения позволяют
с большой точностью
определять расстояния
до небесных тел
Солнечной системы.
Этим методом
уточнены расстояния
до Луны, Венеры,
Меркурия, Марса,
Юпитера
12.
3. Лазерная локацияМетод аналогичен
радиолокации, однако
точность гораздо
выше.
Лазерная локация
позволяет определять
расстояния между
точками лунной и
земной поверхности с
точностью до
сантиметров
13.
4. Определение размеров телСолнечной системы
При наблюдениях небесных тел Солнечной
системы можно измерить угол ρ, под
которым они видны земному наблюдателю
14.
4. Определение размеров телСолнечной системы
Зная этот угловой радиус светила ρ и
расстояние до светила D, можно вычислить
линейный радиус R:
R D sin
15.
4. Определение размеров телСолнечной системы
Учитывая ранее полученную формулу для D,
получим:
sin
R
R
sin p0
16.
4. Определение размеров телСолнечной системы
А так как углы малы, то:
R
p0
R
17.
Во сколько раз линейный радиусСолнца превышает радиус Земли,
если угловой радиус Солнца 16´?
Дано:
Решение
16 16 60
p 8,8
R
R ?
p
R
16 60
R
R
8,8
R 109 R















 Астрономия
Астрономия








