Методы решения тригонометрических уравнений

1.

Методы решения
тригонометрических
уравнений
ВЫПОЛНИЛА УЧЕНИЦА 10 «А» КЛАССА
СИНЕЛЬНИКОВА МАЙЯ

2.

Метод
замены
переменной
помощью замены t = sinx или t = cosx, где
С
t ∈ [−1;1]
решение исходного уравнения сводится к решению
квадратного или другого алгебраического уравнения.
Иногда используют универсальную тригонометрическую
x
подстановку: t = tg
2
α
1 tg
1 t2
2
cos α
2
α
1
t
2
1 tg
2
2
α
2tg
2t
2
sin α
2
α
1
t
2
1 tg
2

3.

2 sin 2 x 5 sin x 2 0
Пусть sin x t , где t 1; 1 , тогда
2t 2 5t 2 0
t1 2, не удовлетворяет условию t 1; 1
t 2 1 ;
2
Вернемся к исходной переменной
1
sin x
2
x 1 arcsin
n
x 1
n
1
πn , n Z
2
π
πn , n Z
6
π
Ответ : 1
πn , n Z .
6
n

4.

на множители
Суть Метод
этого разложения
метода заключается
в том, что
произведение нескольких множителей равно нулю,
если хотя бы один из них равен нулю, а другие при
этом не теряют смысл:
f(x) · g(x) · h(x) · … = 0
⟺ f(x) = 0 или g(x) = 0 или h(x) = 0
и т.д. при условии существования каждого из сомножителей

5.

1
2
sin x cos x 0
3
5
1
sin x 3 0,
cos x 2 0;
5
x
x
1
sin
x
,
3
cos x 2 ;
5
1
1
n
n
x 1 arcsin πn , n Z
1 arcsin πn , n Z
3
3
2
2
x
π
arccos
arccos 2πk , k Z
2πk , k Z
5
5
Ответ : 1 arcsin
n
1
2
πn ; π arccos 2πk ; n ,k Z .
3
5

6.

Однородные тригонометрические уравнения
Уравнение вида a sin x + b cos x = 0 называют
однородным тригонометрическим уравнением
первой степени.
a sin x + b cos x = 0
: cos x
a sin x b cos x
0
cos x + cos x = cos x
a tg x + b = 0
b
tg x = –
a
Деление на cos x допустимо, поскольку решения
уравнения cos x = 0 не являются решениями
уравнения a sin x + b cos x = 0.

7.

Однородные тригонометрические уравнения
Уравнение вида a sin2x + b sin x cos x + c cos2x = 0
называют однородным тригонометрическим
уравнением второй степени.
: cos2x
a sin2x + b sin x cos x + c cos2x = 0
a sin2x
b sin x cos x
c cos2x
0
+
=
+
2x
2
2
cos
cos x
cos2x
cos x
a tg2x + b tg x + c = 0
Далее, вводим новую переменную tg x = t и решаем
методом замены переменной.
Если в данном уравнении а = 0 или с = 0 то,
уравнение решается методом разложения
на множители.

8.

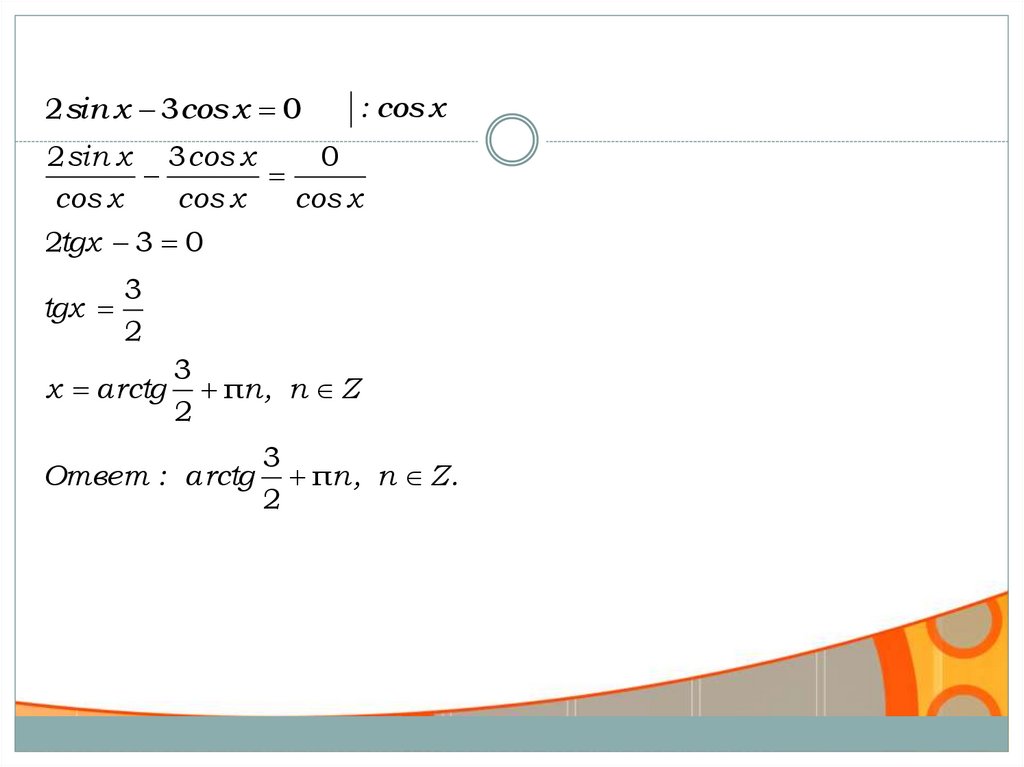
2sin x 3cos x 0
: cos x
2 sin x 3 cos x
0
cos x
cos x
cos x
2tgx 3 0
tgx
3
2
3
x arctg πn , n Z
2
Ответ : arctg
3
πn , n Z .
2

9.

С помощью тригонометрических формул
1. Формулы сложения:
sin (x + y) = sinx cosy + cosx siny
sin (x − y) = sinx cosy + cosx siny
cos (x + y) = cosx cosy − sinx siny
cos (x − y) = cosx cosy + sinx siny
tg (x + y) =
tg (x − y) =
tgx + tgy
1 − tgx tgy
tgx − tgy
1 + tgx tgy
сtgx сtgy − 1
сtg (x + y) =
сtgу + с tgх
сtgx сtgy + 1
сtg (x − y) =
сtgу − с tgх

10.

3 cos x sin x 1
:2
3
1
1
cos x sin x
2
2
2
3
π 1
π
Заметим, что
cos ,
sin , тогда
2
6 2
6
π
π
1
cos cos x sin sin x
6
6
2
π
1
cos x
6
2
π
1
x arccos 2πn , n Z
6
2
π π
x 2πn , n Z
3 6
π π
Ответ : 2πn , n Z .
3 6

11.

С помощью тригонометрических формул
2. Формулы приведения:
π
sin t cos t
2
sin π t sin t
π
cos t sin t
2
cos π t cos t
3π
sin
t cos t
2
3π
cos
t sin t
2
sin 2π t sin t
cos 2π t cos t
π
tg t ctg t
2
tg π t tg t
π
ctg t tg t
2
ctg π t ctg t
3π
tg
t ctg t
2
tg 2π t tg t
3π
ctg
t tg t
2
ctg 2π t ctg t

12.

С помощью тригонометрических формул
3. Формулы двойного аргумента:
sin 2x = 2sinx cosx
cos 2x = cos2x – sin2x
2tgx
tg 2x =
1 – tg2x
ctg2x – 1
ctg 2x =
2ctgx
cos 2x = 2cos2x – 1
cos 2x = 1 – 2sin2x

13.

sin 4x cos 2x 0
2sin 2x cos 2x cos 2x 0
cos 2x 2sin 2x 1 0
cos 2x 0,
2 sin 2x 1 0;
cos 2x 0,
sin 2x 1 ;
2
π
2
x
πn , n Z
2
2x 1 k arcsin 1 πk , k Z
2
Ответ :
π πn
,n Z;
4
2
π πn
x
,n Z
4
2
x 1 k π πk , k Z
12
2
π πk
1
, k Z.
12
2
k

14.

С помощью тригонометрических формул
4. Формулы понижения степени:
sin 2 α
1
1 cos 2α
2
1
cos α 1 cos 2α
2
2
sin α cos α
1
sin 2α
2
sin α cos α 2 1 sin 2α
5. Формулы половинного угла:
α
1 cos α
sin
2
2
α
sin α
1 cos α
tg
2 1 cos α
sin α
α
1 cos α
cos
2
2
α
sin α
1 cos α
ctg
2 1 cos α
sin α

15.

С помощью тригонометрических формул
6. Формулы суммы и разности:
cos α cos β 2cos
α β
α β
cos
2
2
α β
β α
cos α cos β 2 sin
sin
2
2
sin α sin β 2 sin
α β
α β
cos
2
2
α β
α β
sin α sin β 2 sin
cos
2
2
sin( α β )
tg α tg β
cos α cos β
sin( α β )
tg α tg β
cos α cos β
sin( α β )
ctg α ctg β
sin α sin β
ctg α ctg β
sin( β α )
sin α sin β

16.

С помощью тригонометрических формул
7. Формулы произведения:
1
cos α cos β cos α β cos α β
2
1
sin α sin β cos α β cos α β
2
1
sin α cos β sin α β sin α β
2