Вписанная и описанная окружность. 9 класс

1.

13.01.21
Классная работа
Вписанная и описанная
окружность

2.

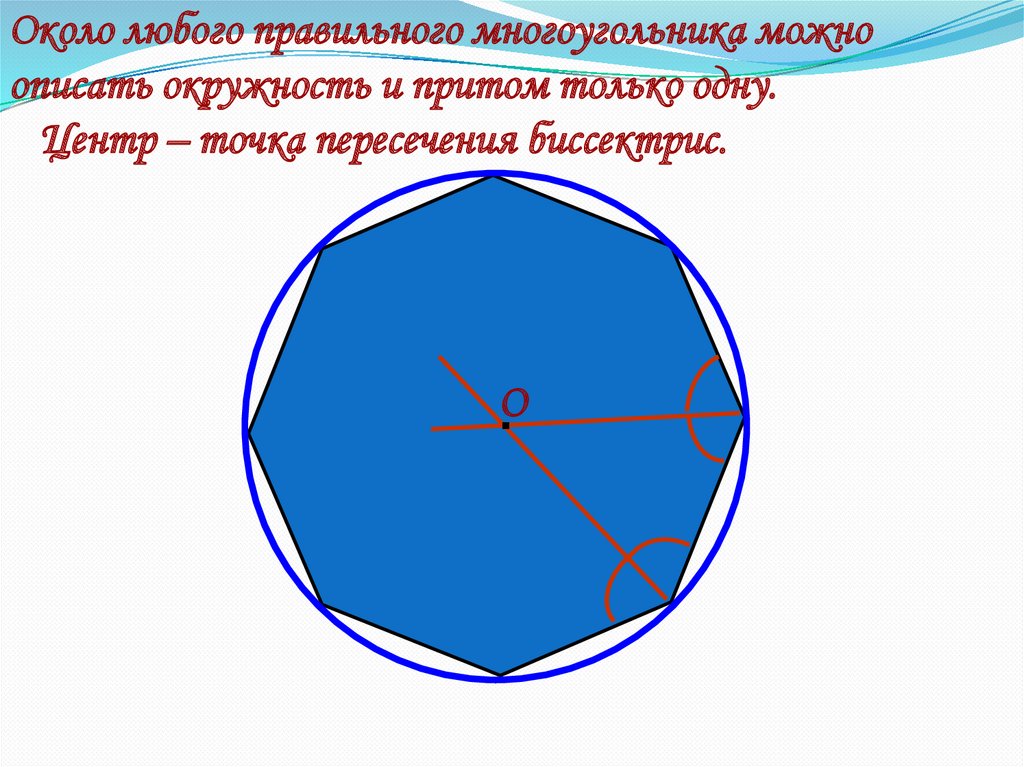
Около любого правильного многоугольника можно
описать окружность и притом только одну.
Центр – точка пересечения биссектрис.
О
·

3.

∟
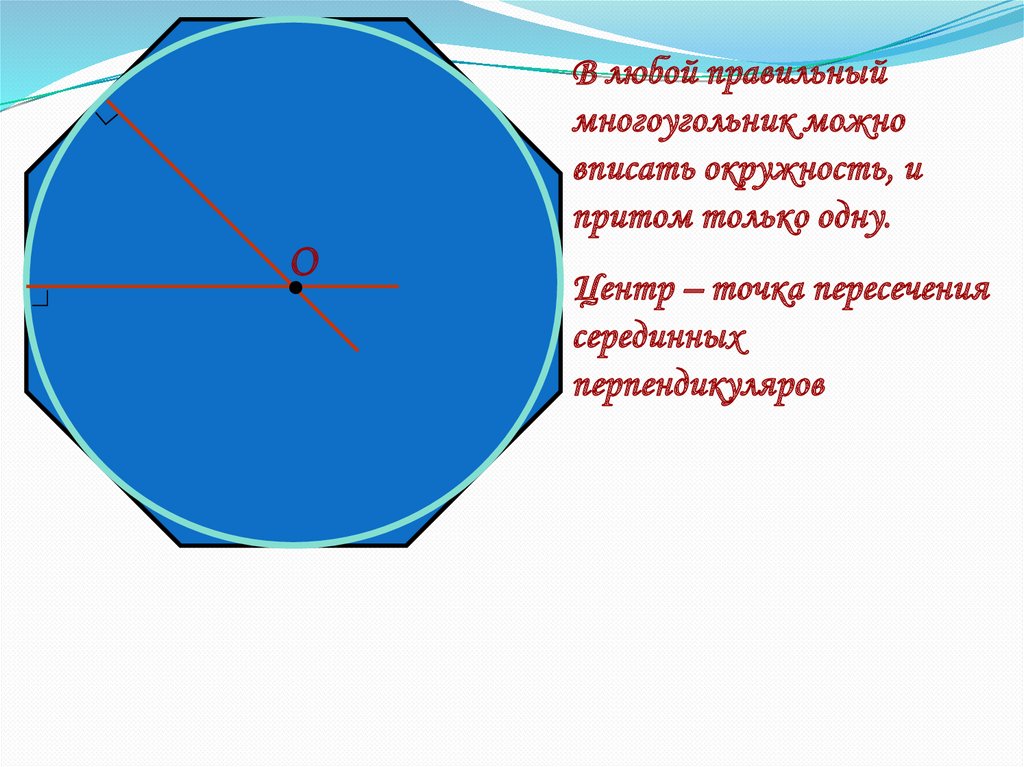
В любой правильный
многоугольник можно
вписать окружность, и
притом только одну.
О
Центр – точка пересечения
серединных
перпендикуляров

4.

Построение правильных
многоугольников

5.

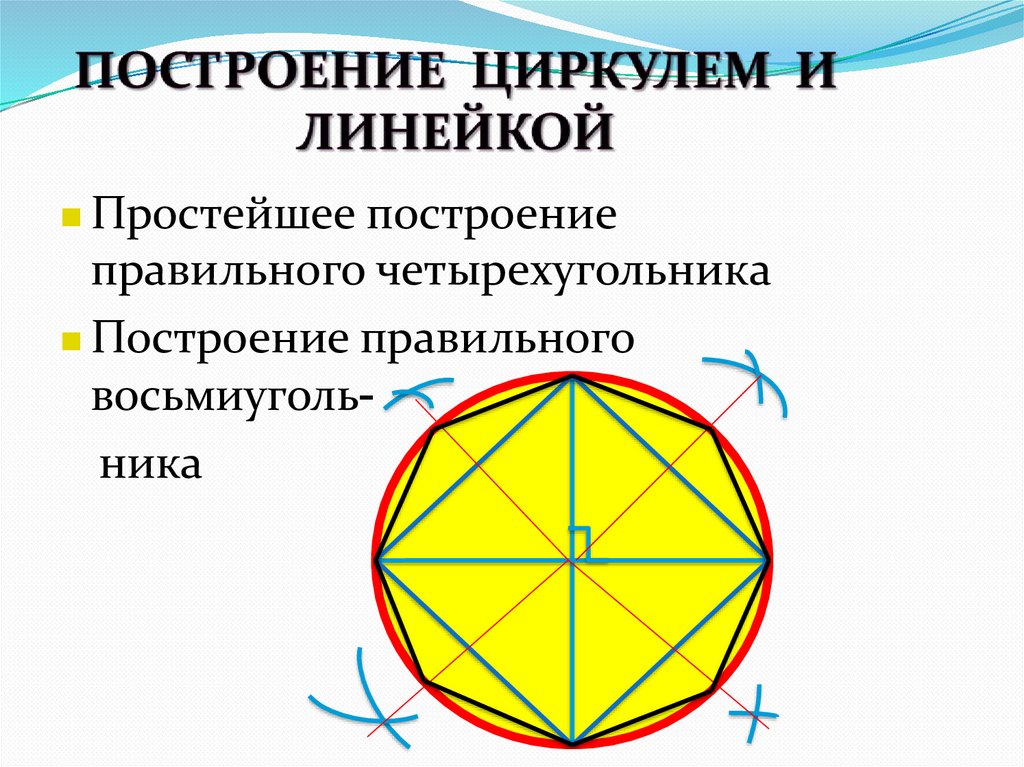
Простейшее
построение
правильного четырехугольника
Построение правильного
восьмиугольника

6.

1.
2.
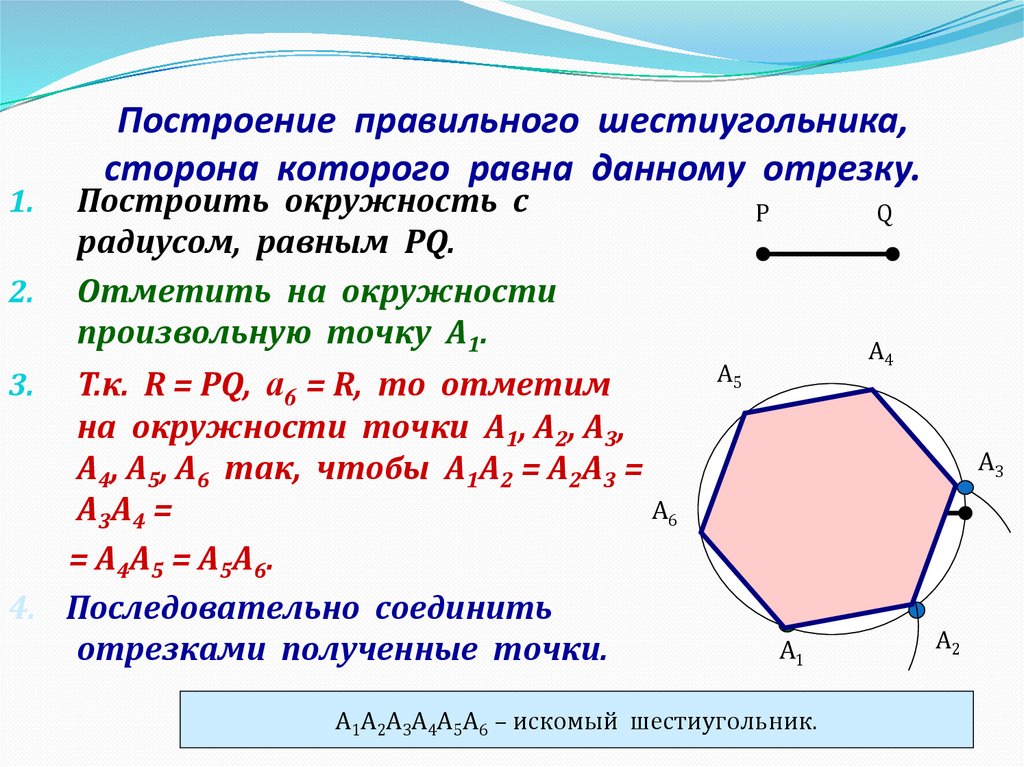
Построение правильного шестиугольника,
сторона которого равна данному отрезку.
Построить окружность с
радиусом, равным PQ.
Отметить на окружности
произвольную точку А1.
Т.к. R = PQ, а6 = R, то отметим
на окружности точки А1, А2, А3,
А4, А5, А6 так, чтобы А1А2 = А2А3 =
А6
А3А4 =
= А4А5 = А5А6.
4. Последовательно соединить
отрезками полученные точки.
3.
P
Q
А4
А5
А3
А1
А1А2А3А4А5А6 – искомый шестиугольник.
А2

7.

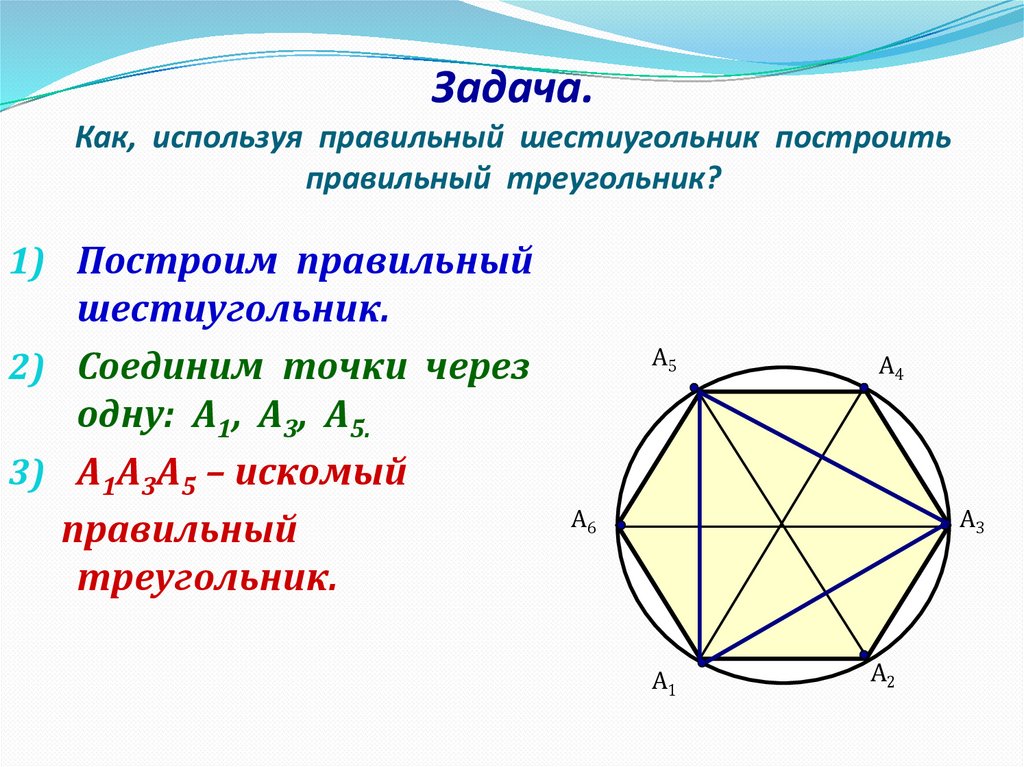
Задача.
Как, используя правильный шестиугольник построить
правильный треугольник?
1) Построим правильный
шестиугольник.
А5
2) Соединим точки через
одну: А1, А3, А5.
3) А1А3А5 – искомый
правильный
треугольник.
А4
А6
А3
А1
А2

8.

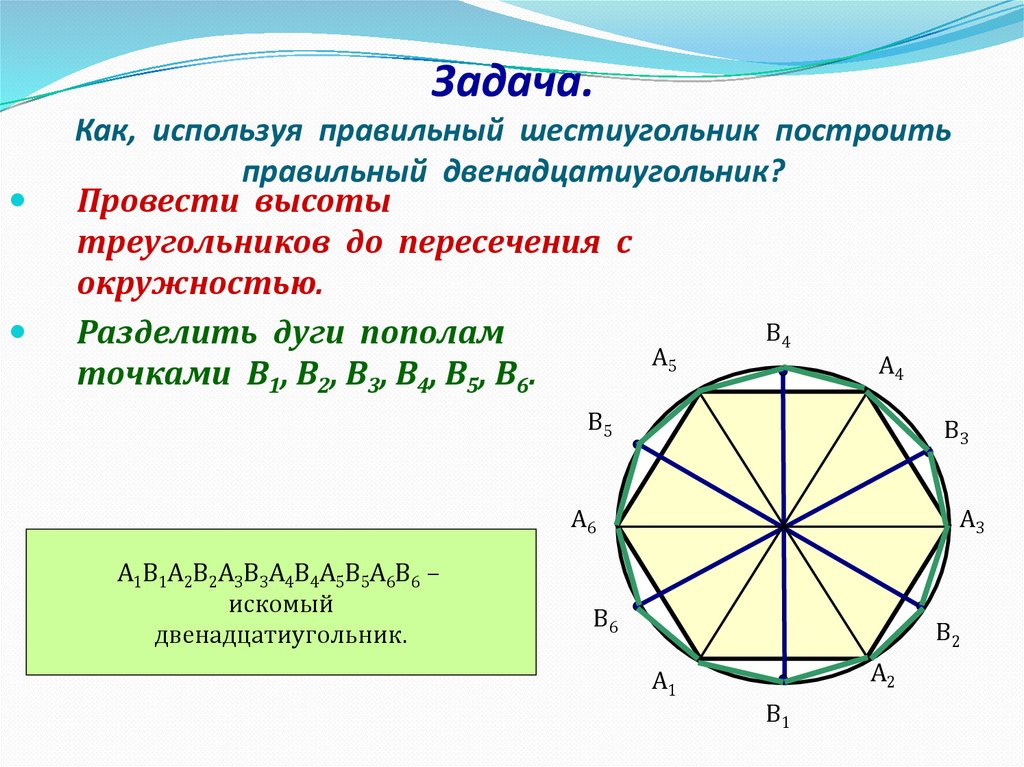
Задача.
Как, используя правильный шестиугольник построить
правильный двенадцатиугольник?
Провести высоты
треугольников до пересечения с
окружностью.
В4
Разделить дуги пополам
А5
А4
точками В1, В2, В3, В4, В5, В6.
В5
В3
А6
А1В1А2В2А3В3А4В4А5В5А6В6 –
искомый
двенадцатиугольник.
А3
В6
В2
А1
А2
В1

9.

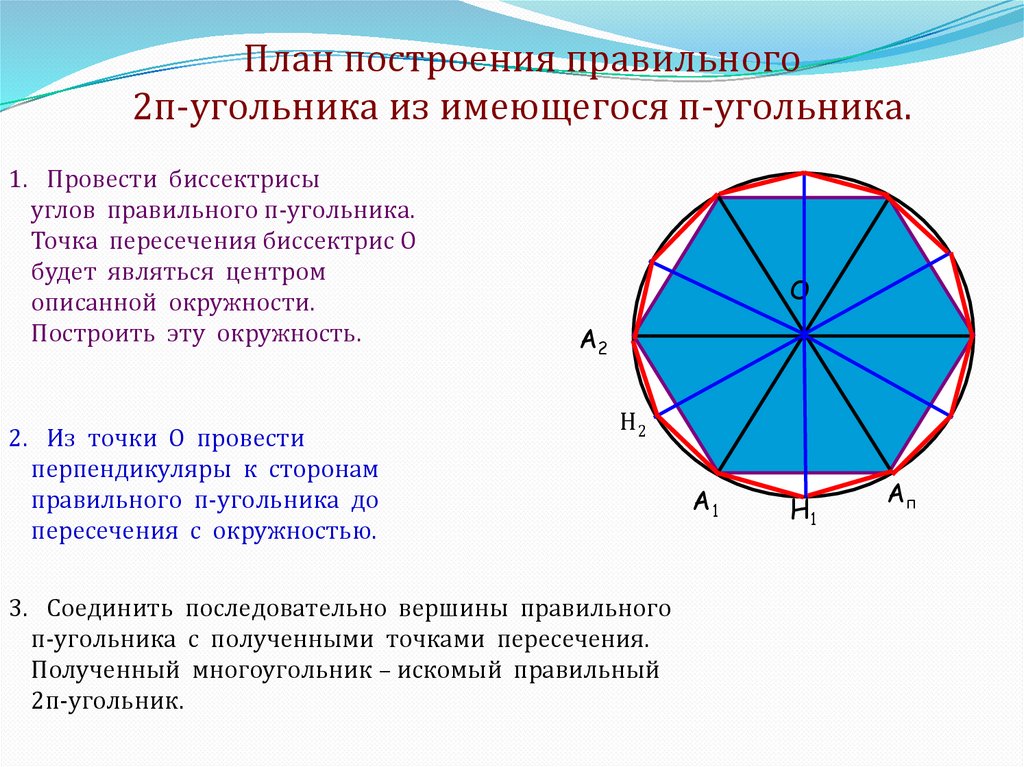
План построения правильного
2п-угольника из имеющегося п-угольника.
1. Провести биссектрисы
углов правильного п-угольника.
Точка пересечения биссектрис О
будет являться центром
описанной окружности.
Построить эту окружность.
2. Из точки О провести
перпендикуляры к сторонам
правильного п-угольника до
пересечения с окружностью.
О
А2
Н2
3. Соединить последовательно вершины правильного
п-угольника с полученными точками пересечения.
Полученный многоугольник – искомый правильный
2п-угольник.
А1
Н1
Ап

10.

ДОМА:
На листе формата А4построить :
Правильные треугольник;
четырехугольник,
шестиугольник,
восьми угольник;
двенадцатиугольник (вписанные в окружность )