Похожие презентации:
Решение задач по теме «Правильный многоугольник»
1. Решение задач по теме «ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК».
МОУ СОШ № 8 г. Аткарск9 класс.
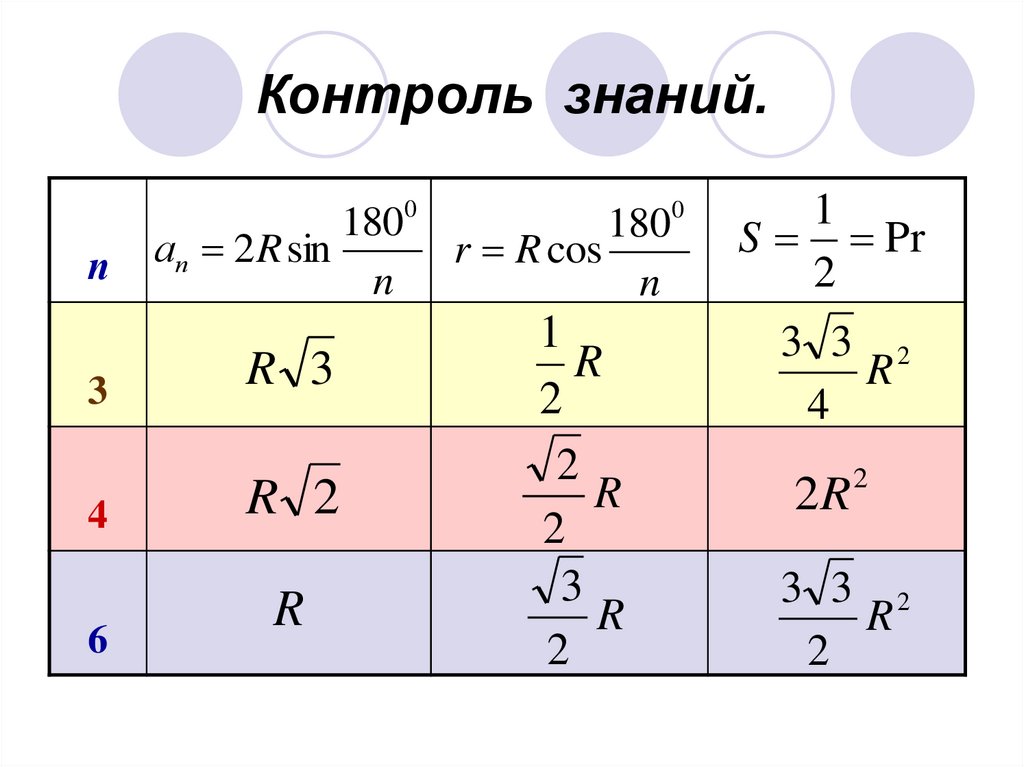
2. Контроль знаний.
п3
4
6
1800
1800
ап 2 R sin
r R cos
n
n
R 3
R 2
R
1
R
2
2
R
2
3
R
2
1
S Pr
2
3 3 2
R
4
2R
2
3 3 2
R
2
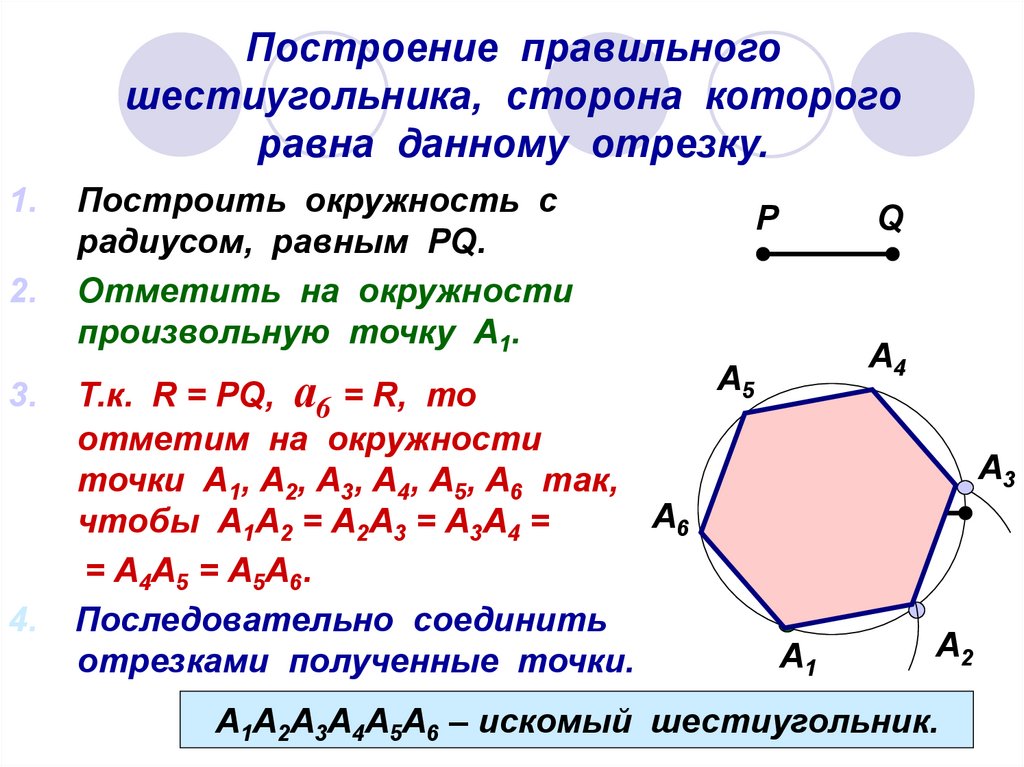
3. Построение правильного шестиугольника, сторона которого равна данному отрезку.
Какая зависимость существует междустороной правильного шестиугольника и
радиусом описанной около него окружности?
Ответ: a6 = R
Пусть РQ – заданный отрезок, равный
стороне правильного шестиугольника,
который нам необходимо построить. Чему
равен радиус описанной около этого
шестиугольника окружности?
Ответ: PQ.
Составьте план построения правильного
шестиугольника со стороной РQ.
4. Построение правильного шестиугольника, сторона которого равна данному отрезку.
1.2.
3.
4.
Построить окружность с
радиусом, равным PQ.
Отметить на окружности
произвольную точку А1.
P
А5
Т.к. R = PQ, а6 = R, то
отметим на окружности
точки А1, А2, А3, А4, А5, А6 так,
А6
чтобы А1А2 = А2А3 = А3А4 =
= А4А5 = А5А6.
Последовательно соединить
А1
отрезками полученные точки.
Q
А4
А3
А2
А1А2А3А4А5А6 – искомый шестиугольник.
5. Задача. Как, используя правильный шестиугольник построить правильный треугольник?
1) Построим правильныйшестиугольник.
2) Соединим точки через
одну: А1, А3, А5.
3) А1А3А5 – искомый
А6
правильный
треугольник.
А5
А4
А3
А1
А2
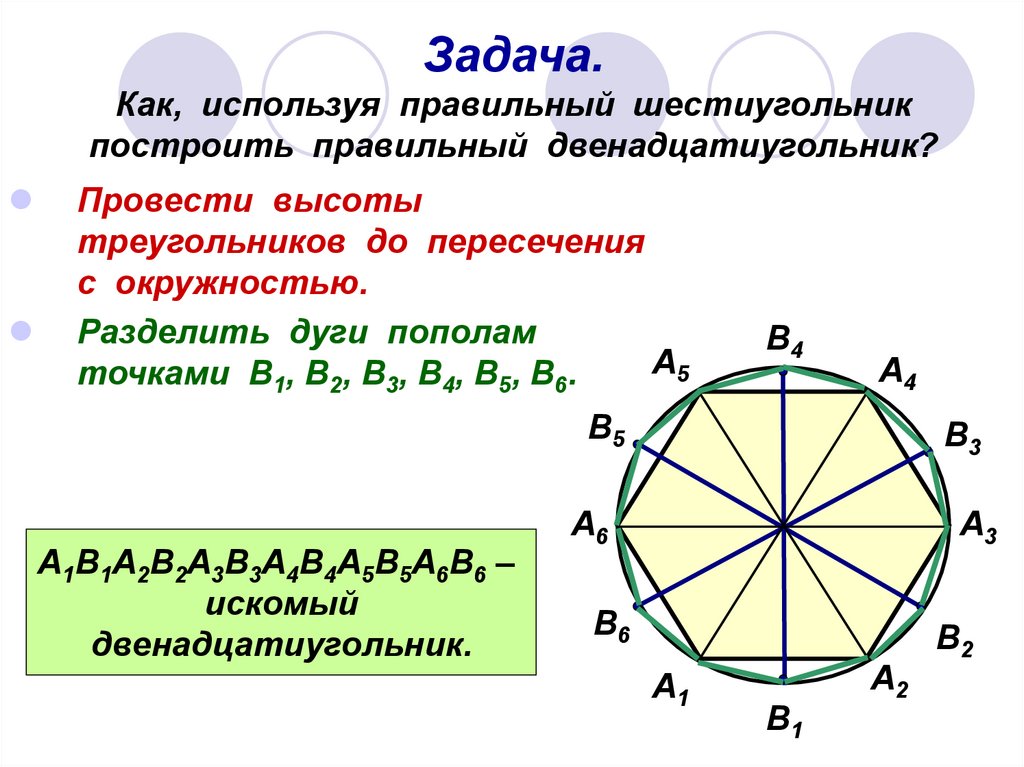
6. Задача. Как, используя правильный шестиугольник построить правильный двенадцатиугольник?
Провести высотытреугольников до пересечения
с окружностью.
Разделить дуги пополам
А5
точками В1, В2, В3, В4, В5, В6.
В4
А4
В5
А1В1А2В2А3В3А4В4А5В5А6В6 –
искомый
двенадцатиугольник.
В3
А6
А3
В6
А1
В1
А2
В2
7.
План построения правильного2п-угольника из имеющегося п-угольника.
1. Провести биссектрисы
углов правильного п-угольника.
Точка пересечения биссектрис О
будет являться центром
А2
описанной окружности.
Построить эту окружность.
Н2
2. Из точки О провести
О
перпендикуляры к сторонам
Ап
А1
Н
1
правильного п-угольника до
пересечения с окружностью.
3. Соединить последовательно вершины правильного
п-угольника с полученными точками пересечения.
Полученный многоугольник – искомый правильный
2п-угольник.
8. Домашнее задание:
П.109, №№ 1094;1100 ( в, г )





 Математика
Математика








