Математическое моделирование подавления волны горения при различных внешних воздействиях

1. ФГБОУ ВПО Нижегородский государственный технический университет им. Р.Е. Алексеева

И.В. Беляев
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОДАВЛЕНИЯ
ВОЛНЫ ГОРЕНИЯ ПРИ РАЗЛИЧНЫХ ВНЕШНИХ
ВОЗДЕЙСТВИЯХ
Специальность 01.02.05 – Механика жидкости, газа и плазмы
Диссертация на соискание ученой степени кандидата физико-математических наук
Научный руководитель:
д.ф.-м.н., Л.Ю. Катаева
Нижний Новгород, 2016
1

2. АКТУАЛЬНОСТЬ

• Повреждение и гибель лесов
• Изменение структуры почвы
• Загрязнение атмосферы продуктами
горения
• Задымление территории
• Огромный материальный ущерб
Динамика лесных пожаров
Российской Федерации
за 1992–2014 гг.
Сгорело леса на корню
Площадь ЛП
2
число ЛП

3. ЦЕЛЬ И ЗАДАЧИ

Цель - математическое моделирование и теоретическое исследование
процесса тушения лесного пожара с учетом структуры
растительности и решении задачи о подавлении стационарной
волны горения
Задачи:
• Применить аппарат механики реагирующих сред для моделирования
процессов распространения и подавления волны горения с учетом структуры
растительности при помощи заданного нестационарного потока воды,
естественной и искусственной преграды
• Выявить закономерности подавления волны горения в неоднородном слое
лесных горючих материалов, а также при наличии естественной и
искусственной преграды
• Найти аналитическое решение задачи о распространении волны горения на
основе решения задачи теплового баланса, на основе которого получить
численное решение задачи о подавлении стационарной волны горения в
однородном слое растительности
• Осуществить сравнительный анализ полученных результатов с известными
данными по скорости распространения лесного пожара и критическому
количеству воды, необходимой для тушения лесного пожара
• Разработать программную реализацию данных алгоритмов
3

4. СОДЕРЖАНИЕ РАБОТЫ

Введение
Глава 1.
Обзор работ в области исследования динамики и тушения лесного пожара
Глава 2.
Влияние характеристик лесной растительности и способов подачи воды на
динамику распространения и тушения пожара
Глава 3.
Влияние взаимного положения искусственной и естественной преграды на
эффективность тушения лесного пожара
Глава 4.
Численное и аналитическое моделирование распространения стационарной
волны горения в слое лесных горючих материалов
Заключение
Список литературы
4

5. ПОЛОЖЕНИЯ ВЫНОСИМЫЕ НА ЗАЩИТУ

• Физико-математическое моделирование и влияние структуры лесной
растительности на динамику тушения лесного пожара при помощи
стационарного источника подачи воды.
• Физико-математическое моделирование совместного действия
искусственной и естественной преграды при тушении лесного пожара.
• Аналитическое решение задачи об определении скорости волны
горения от коэффициентов диффузии, рассеяния тепловой энергии,
скорости реакции горения, отношения выделения тепловой энергии к
энергии, необходимой для нагрева до температуры воспламенения.
• Численная зависимость скорости распространения волны горения от
интенсивности оттока тепла в результате её подавления, полученная
на основе аналитического решения задачи о распространении волны
горения.
5

6. ГЛАВА 1. ОБЗОР РАБОТ В ОБЛАСТИ ИССЛЕДОВАНИЯ ДИНАМИКИ И ТУШЕНИЯ ЛЕСНОГО ПОЖАРА

Эмпирические модели
(натурные данные)
• A. McArthur (1966, Австралия);
• Г.П. Коровин (1969, Россия) и др.
Экспериментальноаналитические модели
• R. Rothermel (1972, США);
• Г.А. Доррер (1979, Россия) и др.
(на основе экспериментальных данных получение
упрощенных зависимостей)
• C. Van Wagner (1967, Канада);
• Э.В. Конев, А.И. Сухинин (1977,
Россия)
• А.М. Гришин (1980,Россия)
Физико-математические модели
(законы механики реагирующих сред)
Модели
Эмпирические модели
Экспериментальноаналитические модели
Физико-математические
модели
±
+
±
+
+
+
-
Свойства
Универсальность
Точность
Простота использования
6

7. ГЛАВА 1. ОБЗОР РАБОТ В ОБЛАСТИ ИССЛЕДОВАНИЯ ДИНАМИКИ И ТУШЕНИЯ ЛЕСНОГО ПОЖАРА

Современные исследования свойств и структуры лесной растительности и их влияния
на процесс горения
Свойства растительности:
Абдурагимов И.М., Алексашенко
А.А., Мелехов И.С.
Структура растительности:
Исаева Л.Н., Оболенская А.В.,
Серков Б.Б.
Влияют на:
Скорость горения
Способность воспламенения
7

8. ГЛАВА 1. ОБЗОР РАБОТ В ОБЛАСТИ ИССЛЕДОВАНИЯ ДИНАМИКИ И ТУШЕНИЯ ЛЕСНОГО ПОЖАРА

Современные подходы к решению задачи об определении скорости
распространения волны горения
Открыта детонация: Малляром , Ле Шателье, Бертло и Вьелем (1883 г.)
Сформулировал условия воспламенения: Вант-Гофф
Ввел математическую формулировку условий для самовоспламенения: Н.Н. Семенов
Свел задачу о тепловом взрыве к задаче, включающей в себя уравнение теплового
баланса и химической кинетики: О.М. Тодес
Экспериментальные
1) Мелехов: Зависимость скорости пожаров
от вида горючих материалов
2) Курбатский: зависимость скорости
распространения горения от влажности ЛГМ
3) Нестеров: связь между плотностью
горючих материалов и скоростью
распространения пожара
Теоретические
1) Balbi, J.H: зависимость конфигурации
волны горения от её скорости
2) Гришин: находит скорость
распространения волны горения только в
случае, если известна максимальная
температура
3) Карпов: процесс горения
распространяется с заданной скоростью
8

9. ГЛАВА 2. ВЛИЯНИЕ ХАРАКТЕРИСТИК ЛЕСНОЙ РАСТИТЕЛЬНОСТИ И СПОСОБОВ ПОДАЧИ ВОДЫ НА ДИНАМИКУ РАСПРОСТРАНЕНИЯ И ТУШЕНИЯ ПОЖАРА

Физическая постановка задачи:
Очаг
Прямоугольной
формы
Температура в
очаге 1200 K
Лес
Однородная в
каждом слое
Многофазная
9
Сплошная

10. ГЛАВА 2. ВЛИЯНИЕ ХАРАКТЕРИСТИК ЛЕСНОЙ РАСТИТЕЛЬНОСТИ И СПОСОБОВ ПОДАЧИ ВОДЫ НА ДИНАМИКУ РАСПРОСТРАНЕНИЯ И ТУШЕНИЯ ПОЖАРА

WdV
t
V
G da HdV
V
где V – контрольный объем (ячейка), Г – граница контрольного объема
5
5v
v
5
v
v
pI
5
5C
,
W 3
, 5C v
c
Tv
c
c
T
5 p5
i i pi
5 p5
i 1
0
0
0
Q
t v
Sc
v
v
g
5
5 d
5 Dt C
G
, H R5
T
t
Es
с
4
U
R
k
cU
4
T
3k
s
R
Es q1R1 q2 R2 q3 R3 q4 R4 q5 R5 k s cU R 4 T 4 f x, z , t Te c p 4
q1 6, 85 105 sign T 593K 3,15 105
Mc
Q 1 c R1 R2 R4
R3
M1
10

11. ГЛАВА 2. ВЛИЯНИЕ ХАРАКТЕРИСТИК ЛЕСНОЙ РАСТИТЕЛЬНОСТИ И СПОСОБОВ ПОДАЧИ ВОДЫ НА ДИНАМИКУ РАСПРОСТРАНЕНИЯ И ТУШЕНИЯ ПОЖАРА

E1
k
exp
1
1
1
RT
E2
0 .5
k
T
exp
2 2 2
RT
массовые скорости образования
компонентов газовой фазы
E3
k 3 S 5 3C1 exp
RT
R1
R5 M 1
R
R
3
51
R2
2
M
4
2
R
R 1 T ' i i c pi 5c p 5 , при 4 0 и T Tb
52
1 R R
3 q4 i 1
c 1
5
R4
R f x, z, t , при 4 0 и T Tb
5 0, иначе
Уравнение состояния газовой фазы и
алгебраические соотношения
E
k5 M 2T 2.25 exp 5 x10.25 x2 , x1 0.05,
3
5
C 3
RT
P 5 RT , 1
, C 1, i 1
M
M 1 M 1
E
i 1
k5 M 2T 2.25 exp 5 x1 x 2 , x1 0.05,
RT
11

12. ГЛАВА 2. ВЛИЯНИЕ ХАРАКТЕРИСТИК ЛЕСНОЙ РАСТИТЕЛЬНОСТИ И СПОСОБОВ ПОДАЧИ ВОДЫ НА ДИНАМИКУ РАСПРОСТРАНЕНИЯ И ТУШЕНИЯ ПОЖАРА

Критерии выбора точки для подачи воды
x, z F
x p d p x x p T Tcr ,min
z 1 P T x, z Tcr zmax P T x, z Tcr min
x 1 P T x, z Tcr xmax P T x, z Tcr max
T x, z max
Tcr , min
- минимальное значение температуры среды, куда допускается подача воды
Tcr
- критическая температура, определяемая оператором источника подачи воды
dp
- максимальная дальность подачи воды
12

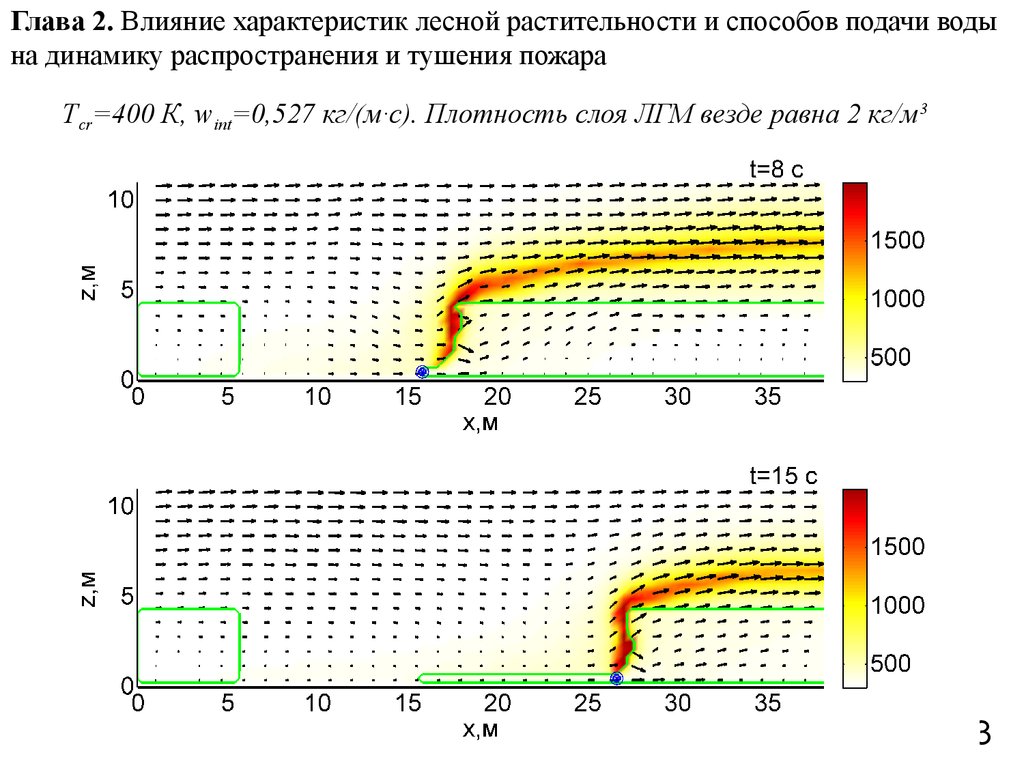
13. Глава 2. Влияние характеристик лесной растительности и способов подачи воды на динамику распространения и тушения пожара

Tcr=400 К, wint=0,527 кг/(м·с). Плотность слоя ЛГМ везде равна 2 кг/м 3
13

14. Глава 2. Влияние характеристик лесной растительности и способов подачи воды на динамику распространения и тушения пожара

Tcr=700 К, wint=0,248 кг/(м·с)
Tcr=700 К, wint=0,249 кг/(м·с)
14

15. Глава 2. Влияние характеристик лесной растительности и способов подачи воды на динамику распространения и тушения пожара

Tcr=700 К, wint=0,249 кг/(м·с). Плотность слоя ЛГМ равна 2 кг/м3
15

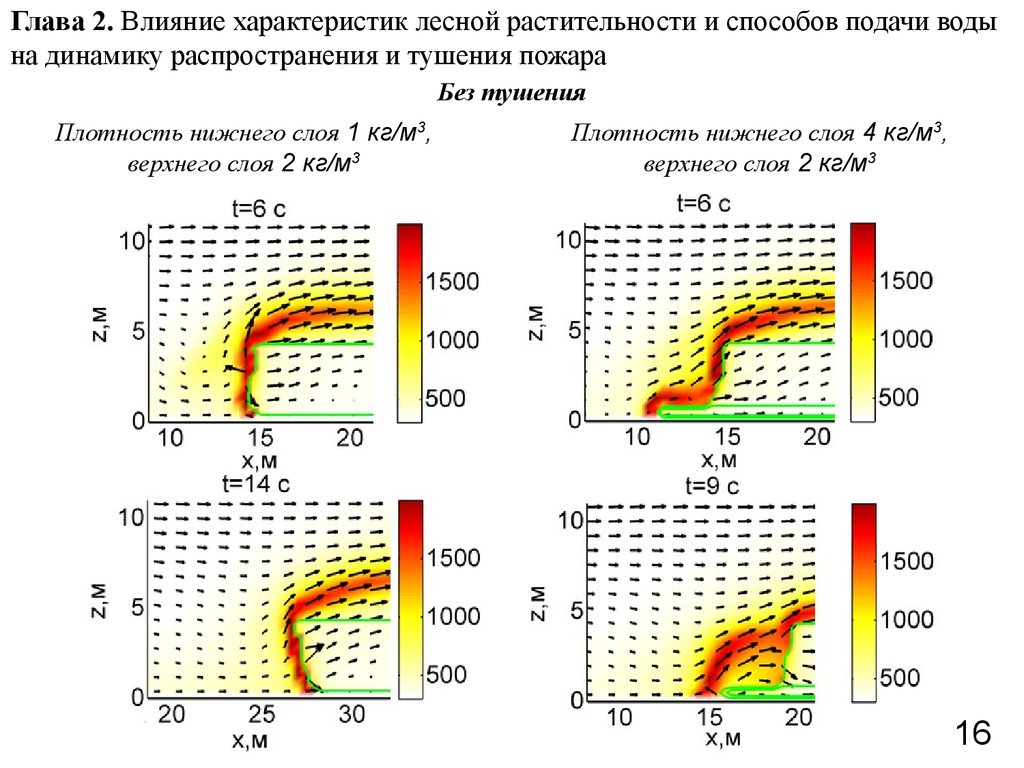
16. Глава 2. Влияние характеристик лесной растительности и способов подачи воды на динамику распространения и тушения пожара

Без тушения
Плотность нижнего слоя 1 кг/м3, 
верхнего слоя 2 кг/м3
Плотность нижнего слоя 4 кг/м3, 
верхнего слоя 2 кг/м3
16

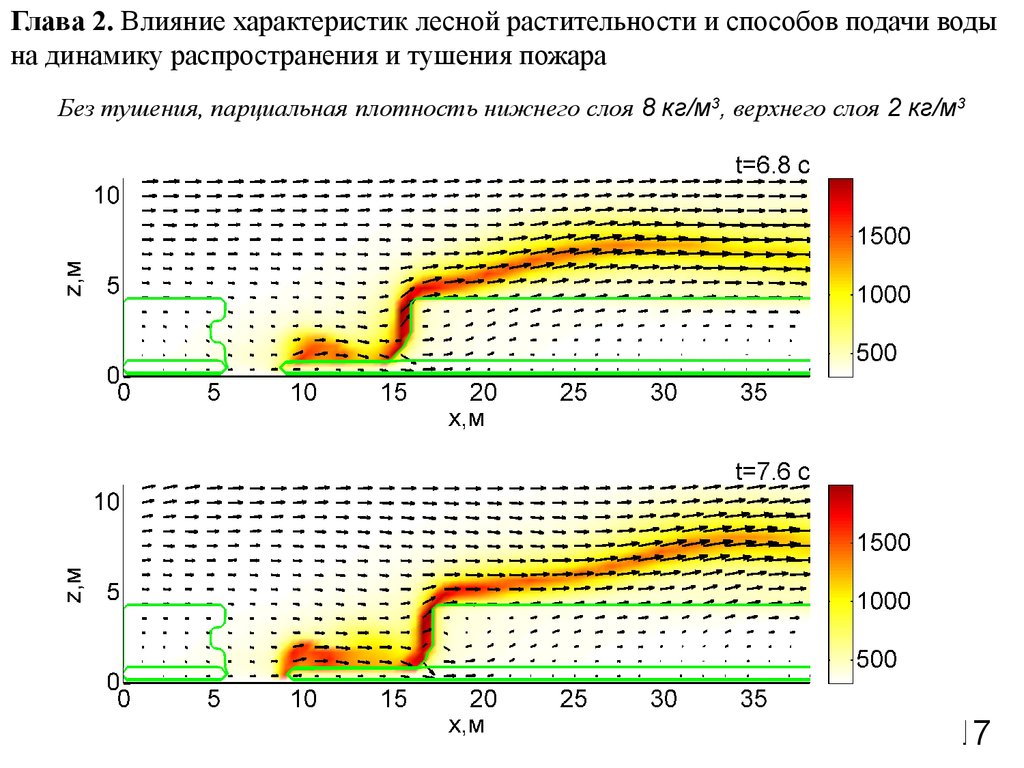
17. Глава 2. Влияние характеристик лесной растительности и способов подачи воды на динамику распространения и тушения пожара

Без тушения, парциальная плотность нижнего слоя 8 кг/м3, верхнего слоя 2 кг/м3
17

18. Глава 2. Влияние характеристик лесной растительности и способов подачи воды на динамику распространения и тушения пожара

Без тушения, парциальная плотность нижнего слоя 8 кг/м3, верхнего слоя 2 кг/м3
18

19. Глава 2. Влияние характеристик лесной растительности и способов подачи воды на динамику распространения и тушения пожара

Зависимость критической интенсивности подачи воды (wint) от плотности нижнего слоя при
критической температуре Tcr =800 К
Плотность нижнего слоя,
1
2
4
8
16
32
3
кг/м
wint, кг/(м·с)
0,2225 0,2665
0,2835
0,6385 0,2435 0,2295
Зависимость критической интенсивности подачи воды от плотности нижнего слоя и
критической температуры
Tcr, К
wint, кг/(м·с)
Плотность нижнего слоя
Плотность нижнего слоя
2 кг/м3
8 кг/м3
500
0,3965
1,4725
600
0,3225
0,9915
700
0,2485
0,8905
800
0,2665
0,6385
900
0,3125
1,0155
1000
0,3955
1,4595
19

20. ГЛАВА 3. Влияние взаимного положения искусственной и естественной преграды на эффективность тушения лесного пожара

Естественная преграда:
источник, увеличивающий влажность лесных горючих материалов (ЛГМ) в
прилегающей к нему области
равномерная по
высоте влажность
неравномерная по
высоте влажность
x x 2
nb
w x we wnb exp
nb
x x 2
2 h f z
nb
w x, z
we wnb exp
nb
hf
Искусственная преграда:
конструкция способная подавать воду в непосредственной близости в объеме,
необходимом для понижения температуры среды до температуры кипения
воды.
20

21. ГЛАВА 3. Влияние взаимного положения искусственной и естественной преграды на эффективность тушения лесного пожара

Равномерное распределение влажности по высоте, wnb=0,25
21

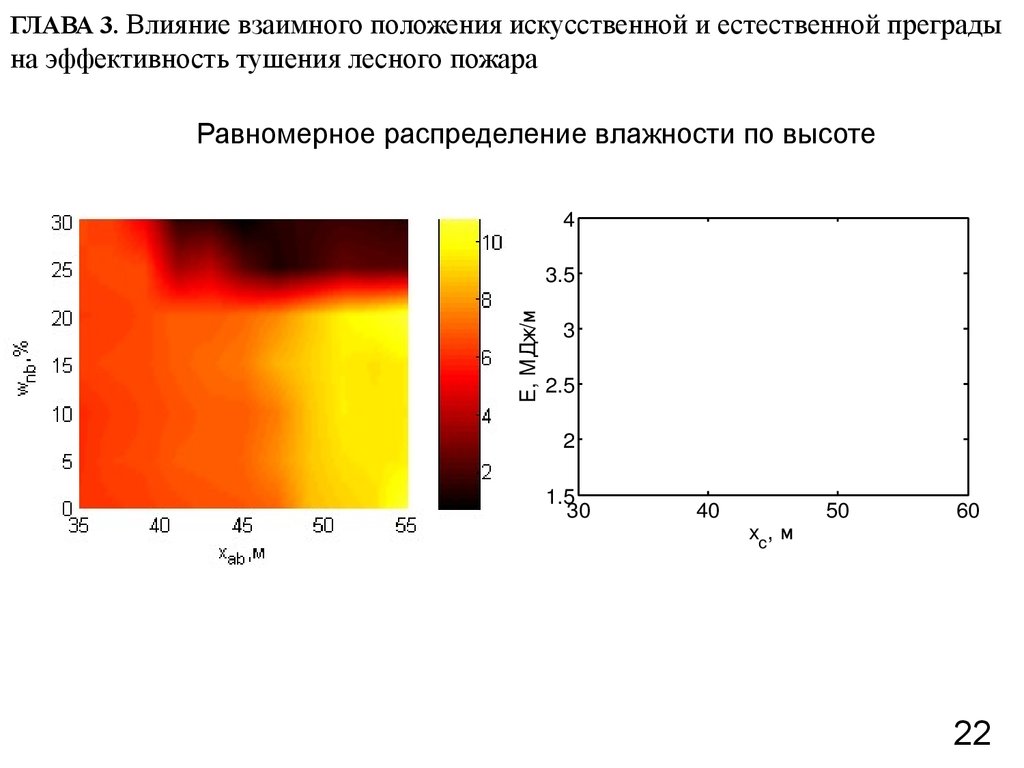
22. ГЛАВА 3. Влияние взаимного положения искусственной и естественной преграды на эффективность тушения лесного пожара

Равномерное распределение влажности по высоте
4
E, МДж/м
3.5
3
2.5
2
1.5
30
40
xc, м
50
60
22

23. ГЛАВА 3. Влияние взаимного положения искусственной и естественной преграды на эффективность тушения лесного пожара

Неравномерное распределение влажности по высоте, без естественной преграды
23

24. ГЛАВА 3. Влияние взаимного положения искусственной и естественной преграды на эффективность тушения лесного пожара

Неравномерное распределение влажности по высоте, wnb=0,3
24

25. ГЛАВА 3. Влияние взаимного положения искусственной и естественной преграды на эффективность тушения лесного пожара

8
E, МДж/м
6
4
2
0
30
40
xc, м
50
60
Неравномерное распределение влажности по высоте
25

26. ГЛАВА 4. Численное и аналитическое моделирование распространения стационарной волны горения в слое лесных горючих материалов

T
v
k T Ta K T Q
t
t
(4.1)
T, K – температура в слое горючих материалов
k, 1/сек – коэффициент теплоотдачи слоя горючего
Ta, К – температура окружающей среды
∆ - оператор Лапласа
K, м2/сек – коэффициент теплопроводности внутри слоя горючих материалов
Q, К – тепловой эффект горения горючих материалов, отнесенный к их удельной
теплоемкости
• p
V  - доля непрореагировавших горючих материалов
t, сек – время
26

27. ГЛАВА 4. Численное и аналитическое моделирование распространения стационарной волны горения в слое лесных горючих материалов

Предполагается, что процесс распространяется с постоянной скоростью c
и вводится переменная:
x
t
c
K
2 ' ' ' k Q v '
c
0
(4.2)
1, 0
v
e , 0
(4.3)
Штрих соответствует производной по автомодельной переменной 4.2
-10
-8
-6
-4
0
-2
0
-0.2
2
4
6
8
10
-0.4
-0.6
-0.8
-1
-1.2
27

28. ГЛАВА 4. Численное и аналитическое моделирование распространения стационарной волны горения в слое лесных горючих материалов

th *
K th
Q th Q
thQ
' ' ' k th
v '
2 2
c *
*
*
uth
cK c
1
c
2
K
K
' ' ' k Q v '
(4.4)
1, 0
v
* , 0
e
k k
(4.5)
(4.6)
1, 0
v
e , 0
C1e 1 C2 e 2 A0 e
(4.7)
(4.8)
28

29.

ГЛАВА 4. Численное и аналитическое моделирование распространения
стационарной волны горения в слое лесных горючих материалов
A 1 1 2
e , 0
1 2
A 1 2 1
e Ae , 0
1 2
1,2
cK2 1
k
1 4 2
c K
(4.9)
(4.10)
2
cK2 Q
A
1 cK2 1 k
(4.11)
29

30.

ГЛАВА 4. Численное и аналитическое моделирование распространения
стационарной волны горения в слое лесных горючих материалов
Введем функцию, зависящую от параметра CKα, заданную следующим образом:
0 с K 0
(4.12)
Процесс распространения волны горения возможен только в случае
выполнения условия:
0 с K 1
(4.13)
2
4
k
c
2
2
K
Q c K
2
c
K
2
c
K
1
2
4
k
c
K
2 1 cK2 1 k
c K2
30
(4.14)

31.

ГЛАВА 4. Численное и аналитическое моделирование распространения
стационарной волны горения в слое лесных горючих материалов
Скорость распространения волны горения будет иметь следующий вид:
c K
2
2
2
Q
4
k
1
Q
1
8
k
Q
1
1
1
1
, Q1 8k 1
2 Q1 k 1
0 , Q1 8k 1
Q1 Q 2k
600
5
T , C
T , C
6
can=0.003468
400
300
4
3
200
2
100
1
­0.5
0
0.5
x­ct, m
(4.16)
7
cnum =0.0034596
500
(4.15)
1
­0.5
0
0.5
x­ct, m
1
Численное и аналитическое решение задачи о распространении волны горения и структура погрешности
численного решения
31

32.

ГЛАВА 4. Численное и аналитическое моделирование распространения
стационарной волны горения в слое лесных горючих материалов
1
F
'
'
'
k
Q
2
c K
cK
0
v '
1, t 0
v t
e , t 0
Итерационный процесс для i-й итерации определен
соотношением:
cK ,i 1 cK QF ,i 1
QF ,i Q
F
c K ,i 1
32
(4.11)

33.

ГЛАВА 4. Численное и аналитическое моделирование распространения
стационарной волны горения в слое лесных горючих материалов
Зависимость скорости распространения пламени по
слою ЛГМ от теплового эффекта реакции горения
33

34.

Спасибо за внимание
34

35.

Справка
35

36. ГЛАВА 2. ВЛИЯНИЕ ХАРАКТЕРИСТИК ЛЕСНОЙ РАСТИТЕЛЬНОСТИ И СПОСОБОВ ПОДАЧИ ВОДЫ НА ДИНАМИКУ РАСПРОСТРАНЕНИЯ И ТУШЕНИЯ ПОЖАРА

Уравнение неразрывности газовой фазы
5 5U 5W
Q
t
x
z
Уравнения сохранения количества движения
5U 5U 2 5UW
P
U U
5 ScdU U 2 W 2 t
t
,
t
x
z
x
x x z z
5W 5UW 5W 2
P
W W
5 ScdW U 2 W 2 t
t
5 g ,
t
x
z
z
x
x z
z
Уравнение сохранения концентраций компонентов газовой фазы
5С 5С U 5С W
C
C
5 Dt 5 Dt R5 , 1,2,
t
x
z
x
x z
z
Уравнение сохранения энергии
4
i i c pi 5c p 5 T
5 c p 5WT
5c p 5UT
i 1
t
x
z
T T
t
t
q1 R1 q2 R2 q3 R3 q4 R4 q5 R5
x x z z
k s cU R 4 T
4
f x, z , t T c
e p4
,
36

37.

Математическая модель лесного пожара
Уравнение сохранения концентраций компонентов газовой фазы
5С 5С U 5С W
C
C
5 Dt 5 Dt R5 , 1,2,
t
x
z
x
x z
z
массовые скорости образования компонентов газовой фазы
R51
R5 M 1
R3
, R52 1 c R1 R5
2M 2
массовые скорости реакций горения летучих продуктов пиролиза
E 5 0.25
2.25
k
M
T
exp
x1 x 2 , x1 0.05
5 2
RT
R5
,
k M T 2.25 exp E 5 x x , x 0.05
5
2
1 2
1
RT
M
Ci
xi 3
, Q 1 c R1 R 2 R 4 c R3
Ck
M1
Mi
k 1 M k
37

38.

Математическая модель лесного пожара
уравнение сохранения объемных долей компонентов твердой фазы
1
M
1
2
R1 , 2
R2 , 3 3 c R1 c R3
t
t
t
M1
массовая скорость реакции пиролиза сухого органического вещества ЛГМ
E
R1 k1 1 1 exp 1
RT
массовая скорость реакции испарения влаги
E
R2 k 2 2 2T 0.5 exp 2
RT
массовая скорость реакции горения конденсированных продуктов пиролиза
E
R3 k3 S 5 3C1 exp 3
RT
Уравнение состояния газовой фазы
Алгебраические соотношения
P
5 RT
M
3
1
C
,
M 1 M
3
4
C 1,
1
i 1
i
1, 4 0
38

39.

1 4
T ' i i c pi 5c p 5 , при 4 0 и T Tb
q4 i 1
R4 f x, z , t , при 4 0 и T Tb
0, при 0 или T T
4
b
39

40.

Граничные и начальные условия
Т e 300 K , с1e 0,23, с2 e 1 10 4 , c3e 1 с1e с2e ,
1e 6 10 3 , 2e 2 10 4 , 3e 2 10 7 , 4e 0, Pe 1,01 105 Па,
1 360 кг 3 , 2 1000 кг 3 , 3 200 кг 3 , 4 1000 кг 3
м
м
м
м
40