Похожие презентации:
Непрерывность функций
1.
Непрерывность функций2.
Непрерывность функцийОпределение №1
Функция y=f(x) называется непрерывной в
точке х0, если выполнены условия:
3.
Непрерывность функцийОпределение №1
Функция y=f(x) называется непрерывной в точке х0, если
выполнены условия:
1. Функция определена в точке х0 , т.е.
определено число f(x0)
4.
Непрерывность функцийОпределение №1
Функция y=f(x) называется непрерывной в точке х0, если
выполнены условия:
1. Функция определена в точке х0 , т.е. определено число
f(x0)
2. Существует конечный предел функции f(x)
при х→ х0
5.
Непрерывность функцийОпределение №1
Функция y=f(x) называется непрерывной в точке х0, если
выполнены условия:
1. Функция определена в точке х0 , т.е. определено число
f(x0)
2. Существует конечный предел функции f(x) при х→ х0
3. Этот предел равен значению функции в этой
точке:
lim f x f x0 .
x x0
6.
Непрерывность функцийОпределение
Функция y=f(x) называется непрерывной в
точке х0 справа (слева), если выполнены
условия:
1. Функция определена в точке х0 , т.е.
определено число f(x0)
7.
Непрерывность функцийОпределение
Функция y=f(x) называется непрерывной в точке х0 справа
(слева), если выполнены условия:
1. Функция определена в точке х0 , т.е. определено число
f(x0)
2. Существует конечный предел функции f(x)
при х→ х0 справа (слева)
3. Этот предел равен значению функции в этой
точке:
lim f x f x0
x x0 0
lim f x f x
0
x
x
0
0
8.
Непрерывность функцийОпределение №2
Если существуют конечные левый и правый
пределы,
равные
между
собой
и
равные
значению функции в точке х0 , то функция y=f(x)
называется непрерывной в этой точке.
Т.е.
lim f x lim f x f x0
x x0 0
x x0 0
9.
Непрерывность функцийПусть функция у = f(x) определена в некотором
интервале (a;b).
Возьмем произвольную точку x0 ϵ (a;b).
10.
Непрерывность функцийПусть функция у = f(x) определена в некотором интервале
(a;b).
Возьмем произвольную точку x0 ϵ (a;b).
Для любого x ϵ (a;b) разность x – x0 называется
приращением аргумента х в точке х0 и
обозначается Δx.
Т.е. Δx = x – x0. Тогда х = х0 + Δх.
11.
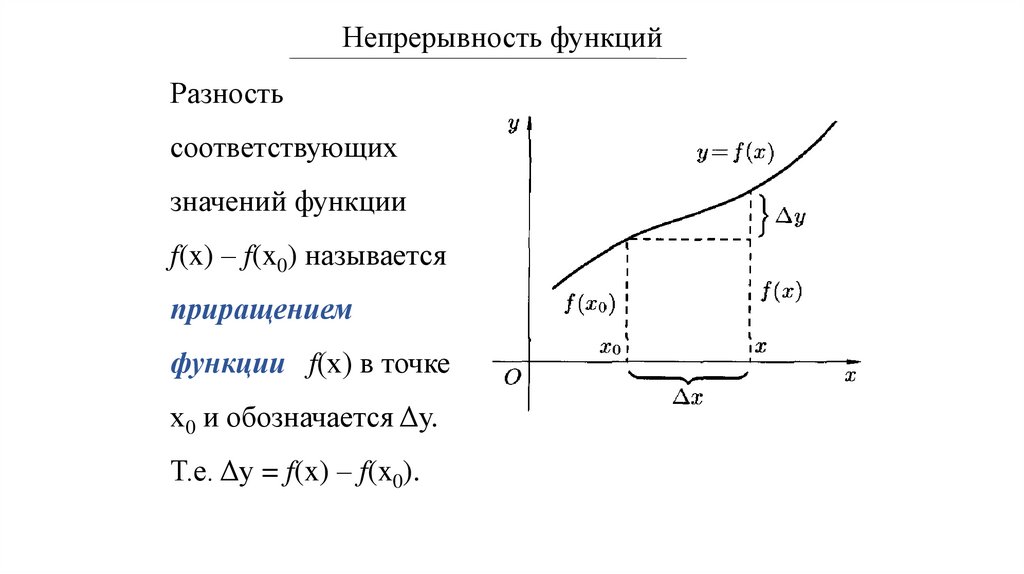
Непрерывность функцийРазность
соответствующих
значений функции
f(x) – f(x0) называется
приращением
функции f(х) в точке
х0 и обозначается Δу.
Т.е. Δу = f(x) – f(x0).
12.
Непрерывность функцийОпределение №3
Функция y=f(x) называется непрерывной в
точке х0 , если ее приращение в этой точке
является бесконечно малой функцией при х→ х0,
т.е.
lim у 0
x 0
13.
Свойства функций, непрерывных в точкеТеорема
Если функции f(x) и g(x) непрерывны в точке х0 ,
то их сумма, разность, произведение и частное
(при g(x)≠0) непрерывны в этой точке.
14.
Свойства функций, непрерывных в точкеТеорема
Если функции f(x) и g(x) непрерывны в точке х0 ,
то их сумма, разность, произведение и частное
(при g(x)≠0) непрерывны в этой точке.
Доказательство следует непосредственно из
соответствующих теорем о пределах.
15.
Свойства функций, непрерывных в точкеТеорема
Если функция g(x) непрерывна в точке х0, а
функция f(g) непрерывна в точке g0, причем
g0 = g(х0), тогда сложная функция f(g(х))
непрерывна в точке х0.
16.
Свойства функций, непрерывных в точкеТеорема
Если
функция
f(x)
имеет
обратную
функцию f -1(у) и непрерывна в точке х0, то
функция f
-1(у)
причем у0 =f(х0).
непрерывна в точке у0,
17.
Свойства функций, непрерывных в точкеТеорема
Всякая элементарная функция непрерывна
в каждой точке, в которой она определена.
18.
Свойства функций, непрерывных в точкеТеорема
Всякая элементарная функция непрерывна в каждой
точке, в которой она определена.
Доказательство:
Пусть f(x) = 7х-3. Докажем, что функция
непрерывна в любой точке х0.
lim f x lim 7 x 3 7 x0 3 f x0
x x0
x x0
19.
Свойства функций, непрерывных в точкеПусть f(x) = sinx. Докажем, что функция
непрерывна в любой точке х0.
20.
Свойства функций, непрерывных в точкеПусть f(x) = sinx. Докажем, что функция непрерывна в
любой точке х0.
lim у lim sin x0 x sin x0
x 0
x 0
21.
Свойства функций, непрерывных в точкеПусть f(x) = sinx. Докажем, что функция непрерывна в
любой точке х0.
lim у lim sin x0 x sin x0
x 0
x 0
2 x0 x
x
lim 2 sin
cos
x 0
2
2
22.
Свойства функций, непрерывных в точкеПусть f(x) = sinx. Докажем, что функция непрерывна в
любой точке х0.
lim у lim sin x0 x sin x0
x 0
x 0
2 x0 x
x
cos
lim 2 sin
x 0
2
2
2 x0 x
lim x cos
0
x 0
2
23.
Свойства функций, непрерывных в точкеПусть f(x) = еx. Докажем, что функция
непрерывна в любой точке х0.
24.
Свойства функций, непрерывных в точкеПусть f(x) = еx. Докажем, что функция
непрерывна в любой точке х0.
lim у lim е
x 0
x 0
x0 x
е
x0
25.
Свойства функций, непрерывных в точкеПусть f(x) = еx. Докажем, что функция непрерывна в
любой точке х0.
x0 x
х
1
lim у lim е
x 0
x 0
х0
lim е е
x 0
е
x0
26.
Свойства функций, непрерывных в точкеx 0 x
х
lim у lim е
x 0
x 0
е
lim е е 1
х0
x 0
lim е х 0
x 0
х0
x0
27.
Точки разрыва функции и ихклассификация
28.
Точки разрыва функции и их классификацияОпределение
Точки, в которых нарушается условие
непрерывности функции называются точками
разрыва этой функции.
29.
Точки разрыва функции и их классификацияОпределение
Точка разрыва х0 называется точкой разрыва
первого рода функции y=f(x), если в этой точке
существуют конечные пределы функции слева
и справа, т. е.
lim f x А1 и
x x0 0
lim f x А2
x x0 0
30.
Точки разрыва функции и их классификацияОпределение
Точка разрыва х0 называется точкой разрыва первого
рода функции y=f(x), если в этой точке существуют
конечные пределы функции слева и справа, т. е.
lim f x А1 и
x x0 0
lim f x А2
x x0 0
При этом:
1.Если А1= А2, то точка х0 называется точкой
устранимого разрыва.
31.
Точки разрыва функции и их классификацияОпределение
Точка разрыва х0 называется точкой разрыва первого рода
функции y=f(x), если в этой точке существуют конечные пределы
функции слева и справа, т. е.
lim f x А1 и
x x0 0
lim f x А2
x x0 0
При этом:
2.Если А1 ≠ А2, точка х0 называется точкой
неустранимого разрыва.
Величина |А1 ̶ А2| называется
скачком
функции.
32.
Точки разрыва функции и их классификацияОпределение
Точка разрыва х0 называется точкой разрыва
второго рода функции y=f(x), если в этой
точке хотя бы один из односторонних
пределов равен бесконечности или не
существует.
33.
Пример 1Исследовать на непрерывность функцию
х 1, 1 х 2,
у
2 х, 2 х 5.
34.
Пример 1Исследовать на непрерывность функцию
х 1, 1 х 2,
у
2 х, 2 х 5.
Найдем односторонние пределы в точке х = 2:
35.
Пример 1Исследовать на непрерывность функцию
х 1, 1 х 2,
у
2 х, 2 х 5.
Найдем односторонние пределы в точке х=2:
lim f x lim х 1 1
x 2 0
x 2 0
36.
Пример 1Исследовать на непрерывность функцию
х 1, 1 х 2,
у
2 х, 2 х 5.
Найдем односторонние пределы в точке х=2:
lim f x lim х 1 1
x 2 0
x 2 0
lim f x lim 2 х 0
x 2 0
x 2 0
37.
Пример 1lim f x lim х 1 1
x 2 0
x 2 0
lim f x lim 2 х 0
x 2 0
x 2 0
Пределы конечны, значит в точке х = 2 разрыв первого рода.
Т.к. 1≠0 х = 2 - точка неустранимого
разрыва.
|1 - 0|=1 – скачок функции.
38.
Пример 2Исследовать на непрерывность функцию
1
у
х 2
39.
Пример 2Исследовать на непрерывность функцию
1
у
х 2
Найдем односторонние пределы в точке х=2:
1
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
40.
Пример 2Исследовать на непрерывность функцию
1
у
х 2
Найдем односторонние пределы в точке х=2:
1
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
1
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
41.
Пример 21
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
1
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
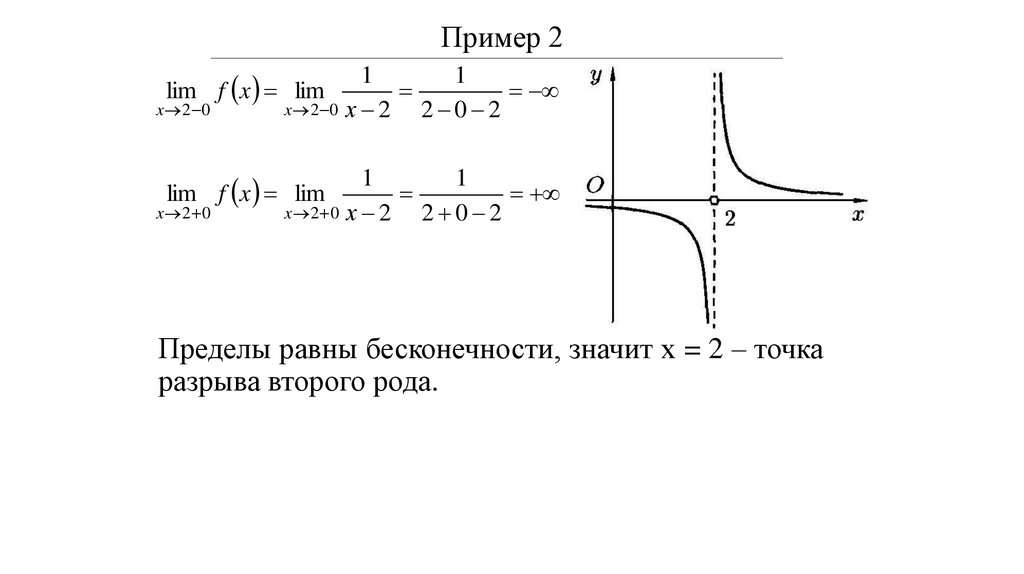
Пределы равны бесконечности, значит х = 2 – точка
разрыва второго рода.
42.
Свойства функций, непрерывныхна отрезке
43.
Свойства функций, непрерывных на отрезкеОпределение
Функция у = f(x) называется непрерывной на
интервале (a;b), если она непрерывна в каждой
точке этого интервала.
44.
Свойства функций, непрерывных на отрезкеОпределение
Функция у = f(x) называется непрерывной на
отрезке [a;b], если она непрерывна на
интервале (a;b) и непрерывна справа в точке a
и слева в точке b.
45.
Свойства функций, непрерывных на отрезкеТеорема Вейерштрасса
Всякая непрерывная на отрезке [a;b] функция
ограничена на нем и достигает на этом отрезке
своего наибольшего и наименьшего значений.
46.
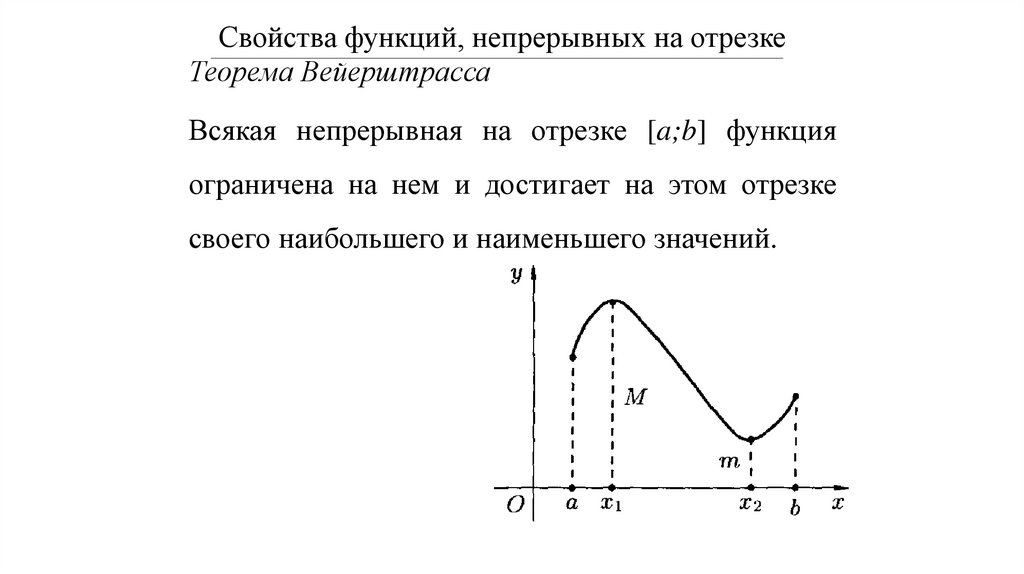
Свойства функций, непрерывных на отрезкеТеорема Вейерштрасса
Всякая непрерывная на отрезке [a;b] функция
ограничена на нем и достигает на этом отрезке
своего наибольшего и наименьшего значений.
47.
Свойства функций, непрерывных на отрезкеТеорема Больцано-Коши
Если функция у = f(x) определена и непрерывна
на отрезке [a;b] и принимает на его концах
неравные значения А и В, тогда для любого числа
С, находящегося между А и В, найдется такое
число с, принадлежащее интервалу (a;b), что
f(с)=С.
48.
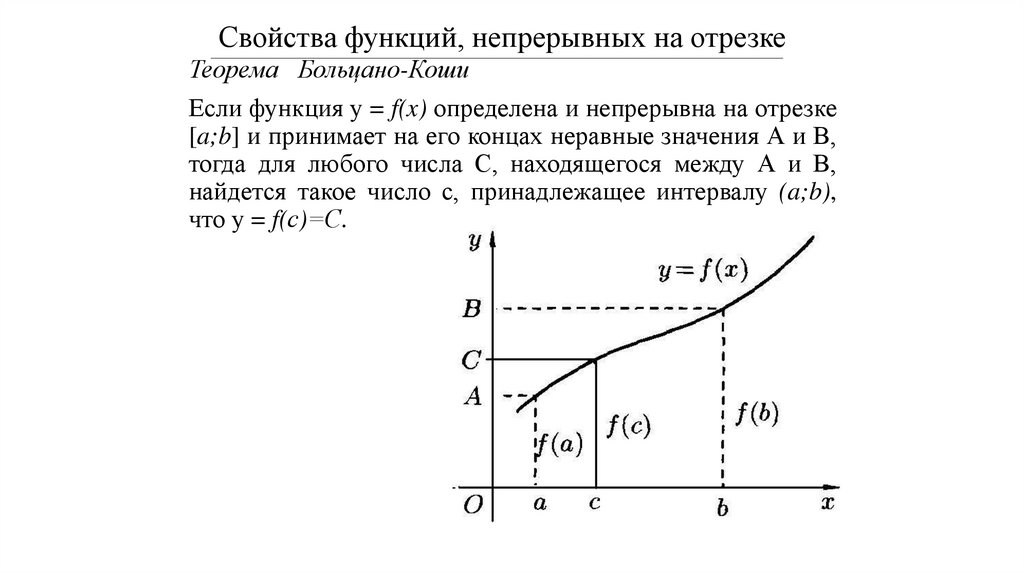
Свойства функций, непрерывных на отрезкеТеорема Больцано-Коши
Если функция у = f(x) определена и непрерывна на отрезке
[a;b] и принимает на его концах неравные значения А и В,
тогда для любого числа С, находящегося между А и В,
найдется такое число с, принадлежащее интервалу (a;b),
что у = f(с)=С.
49.
Свойства функций, непрерывных на отрезкеСледствие
Если функция у = f(x) непрерывна на отрезке
[a;b] и принимает на его концах значения
разных знаков, то внутри этого отрезка
найдется хотя бы одна точка с, в которой
данная функция обращается в нуль: f(с)=0.
50.
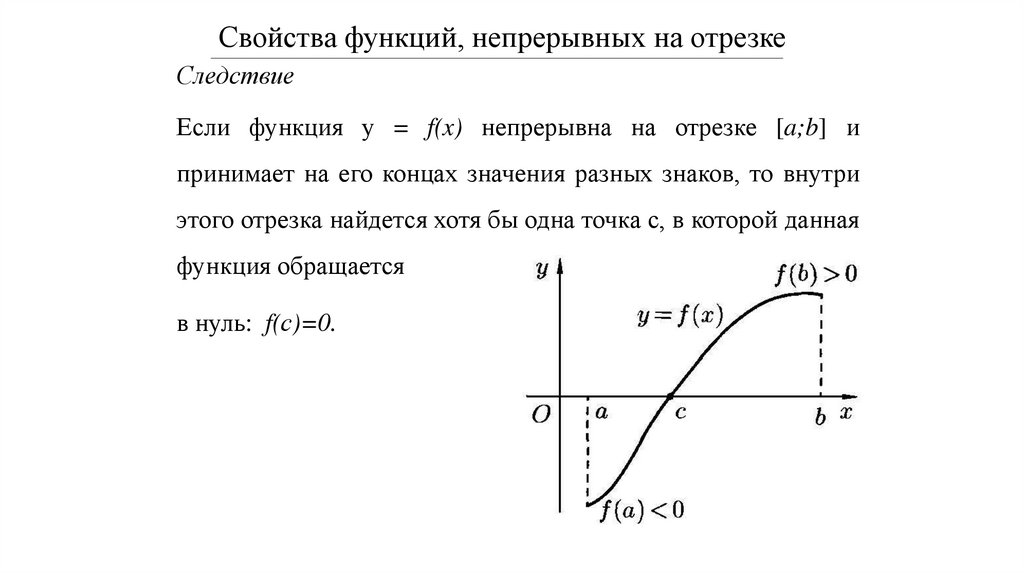
Свойства функций, непрерывных на отрезкеСледствие
Если функция у = f(x) непрерывна на отрезке [a;b] и
принимает на его концах значения разных знаков, то внутри
этого отрезка найдется хотя бы одна точка с, в которой данная
функция обращается
в нуль: f(с)=0.













































 Математика
Математика








