Непрерывные функции и точки разрыва

1.

1. Непрерывность функции в точке
Определение 1
Функция f (x), определенная в окрестности некоторой точки х0, включая саму точку х0, называется
непрерывной в точке х0, если предел функции и значение функции в этой точке равны:
lim f ( x) f ( x0 )
x x0
f (x)
y
х х х0 - приращение аргумента
f
f f ( x) f ( x0 ) f ( x0 x) f ( x0 ) - приращение функции
f ( x0 )
Заметим, что х х0 х х0 0 х 0
х
0
x0
x
x
Следовательно,
lim f ( x) f ( x0 ) lim f ( x) f ( x0 ) 0 lim ( f ( x) f ( x0 )) 0 lim f 0
x x0
x x0
x x0
х 0
Определение 2
Функция f (x), определенная в окрестности некоторой точки х0, включая саму точку х0, называется
непрерывной в точке х0, если предел приращения функции равен 0 при стремлении приращения
аргумента к 0:
lim f 0
х 0
Итак, бесконечно малому приращению аргумента соответствует бесконечно малое приращение
функции в любой точке непрерывности функции:
х 0 f 0

2.

2. Непрерывность функции в интервале и на отрезке
Определение
Функция f (x), называется непрерывной в интервале (a, b), если она непрерывна в каждой точке
этого интервала.
Определение
Функция f (x), называется непрерывной на отрезке [а, b], если она
непрерывна в интервале (a, b),
lim f ( x) f (а) (непрерывность справа), lim f ( x) f (b) (непрерывность слева).
x а
x b
Все простейшие элементарные функции непрерывны в своей области определения
f ( x) С ,
f ( x) sin x,
f ( x) arcsin x,
f ( x) х n ,
f ( x) cos x,
f ( x) tg x,
f ( x) arccos x,
f ( x) arctg x,
f ( x) ctg x,
f ( x) arcctg x
f ( x) a x (a 0, a 1),
f ( x) log a x (a 0, a 1),

3.

3. Свойства непрерывных в точке функций
Пусть функции f (x), g (x) непрерывны в точке х0, тогда функции
f ( x) g ( x),
f ( x) g ( x),
f ( x)
, ( g ( x0 ) 0),
g ( x)
f ( g ( x))
непрерывны в точке х0.
Указанные свойства можно обобщить на случай непрерывности функций
на некотором множестве

4.

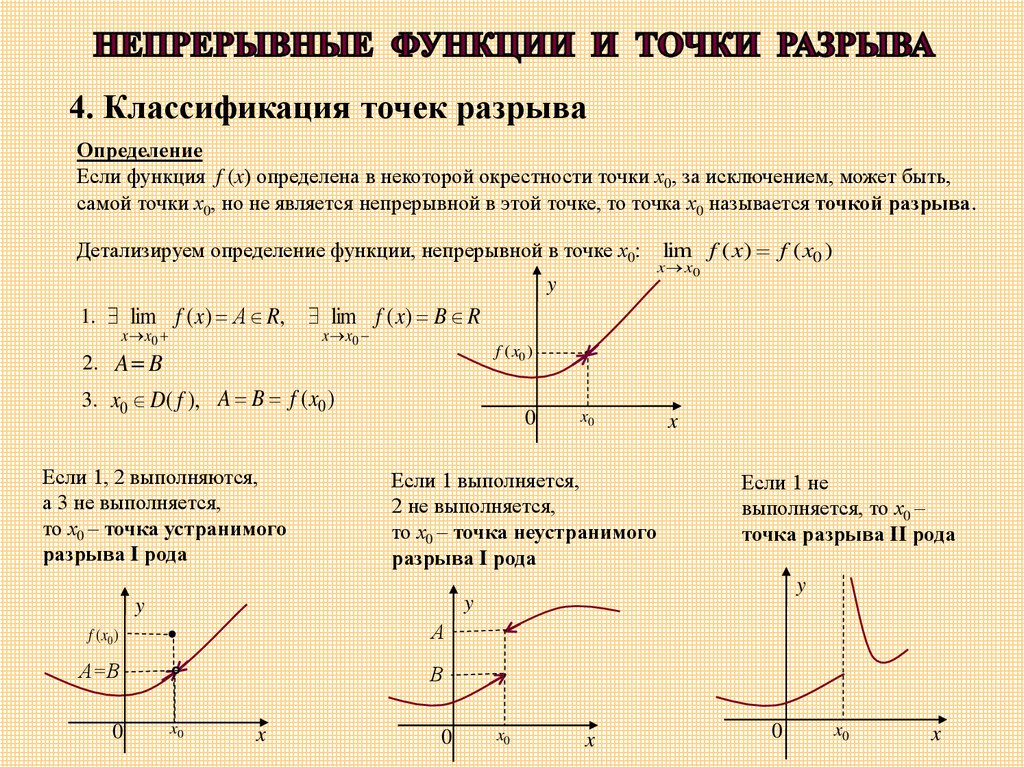
4. Классификация точек разрыва
Определение
Если функция f (x) определена в некоторой окрестности точки х0, за исключением, может быть,
самой точки х0, но не является непрерывной в этой точке, то точка х0 называется точкой разрыва.
Детализируем определение функции, непрерывной в точке х0:
y
1. lim f ( x) А R,
x x0
2. A B
lim f ( x) B R
x x0
f ( x0 )
3. x0 D( f ), A B f ( x0 )
Если 1, 2 выполняются,
а 3 не выполняется,
то х0 – точка устранимого
разрыва I рода
0
x0
Если 1 выполняется,
2 не выполняется,
то х0 – точка неустранимого
разрыва I рода
x
Если 1 не
выполняется, то х0 –
точка разрыва II рода
y
y
y
f ( x0 )
А
А=В
В
0
lim f ( x) f ( x0 )
x x0
x0
x
0
x0
x
0
x0
x

5.

Пусть х0 - внутренняя точка области определения
Рассмотрим условия:
1. lim f ( x) А R,
x x0
lim f ( x) B R
x x0
2. A B
3. x0 D( f ), A B f ( x0 )
1, 2, 3 х0
точка непрерывности
1, 2, 3 х0
точка устранимого
разрыва I рода
1, 2 х0
точка неустранимого
разрыва I рода
1 х0
точка разрыва II рода
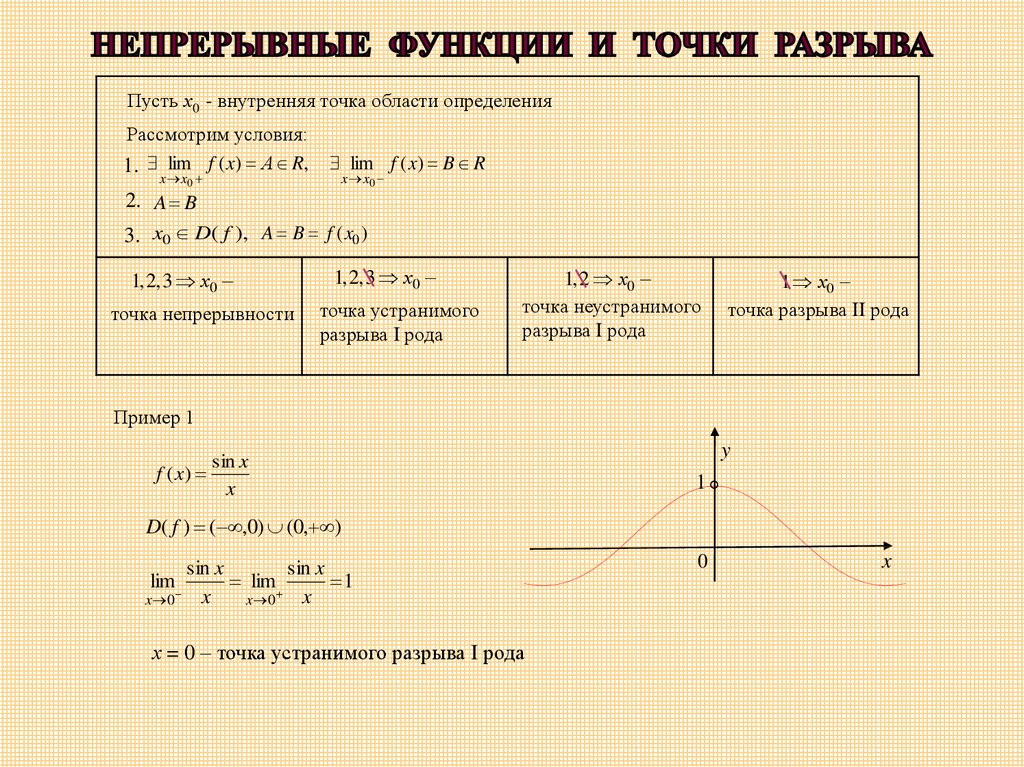
Пример 1
sin x
f ( x)
x
y
1
D( f ) ( ,0) (0, )
sin x
sin x
lim
lim
1
x 0 x
x 0 x
х = 0 – точка устранимого разрыва I рода
0
x

6.

Пусть х0 - внутренняя точка области определения
Рассмотрим условия:
1. lim f ( x) А R,
lim f ( x) B R
x x0
x x0
2. A B
3. x0 D( f ), A B f ( x0 )
1, 2, 3 х0
1, 2, 3 х0
точка непрерывности
точка устранимого
разрыва I рода
1, 2 х0
точка неустранимого
разрыва I рода
1 х0
точка разрыва II рода
Пример 2
y
x 2 1, если x 2;
f ( x)
x 2
1, если x 2
D( f ) ( , 2) ( 2, )
lim f ( x) lim ( 1) 1 R
x 2
x 2
lim f ( x) lim (1) 1 R
x 2
x 2
lim f ( x) lim f ( x)
x 2
x 2
x 2 – точка неустранимого разрыва I рода
1
-2
0
-1
x

7.

Пусть х0 - внутренняя точка области определения
Рассмотрим условия:
1. lim f ( x) А R,
lim f ( x) B R
x x0
x x0
2. A B
3. x0 D( f ), A B f ( x0 )
1, 2, 3 х0
1, 2, 3 х0
точка устранимого
разрыва I рода
точка непрерывности
1, 2 х0
точка неустранимого
разрыва I рода
1 х0
точка разрыва II рода
Пример 3
f
1
( x) 2 x 1
y
D( f ) ( ,1) (1, )
lim f ( x) lim
x 1
x 1
lim f ( x) lim
x 1
1
x
2 1
x 1
0 R
1
x
2 1
x 1 – точка разрыва II рода
0
1
x

8.

Пусть х0 - внутренняя точка области определения
Рассмотрим условия:
1. lim f ( x) А R,
lim f ( x) B R
x x0
x x0
2. A B
3. x0 D( f ), A B f ( x0 )
1, 2, 3 х0
1, 2, 3 х0
точка непрерывности
точка устранимого
разрыва I рода
1, 2 х0
точка неустранимого
разрыва I рода
1 х0
точка разрыва II рода
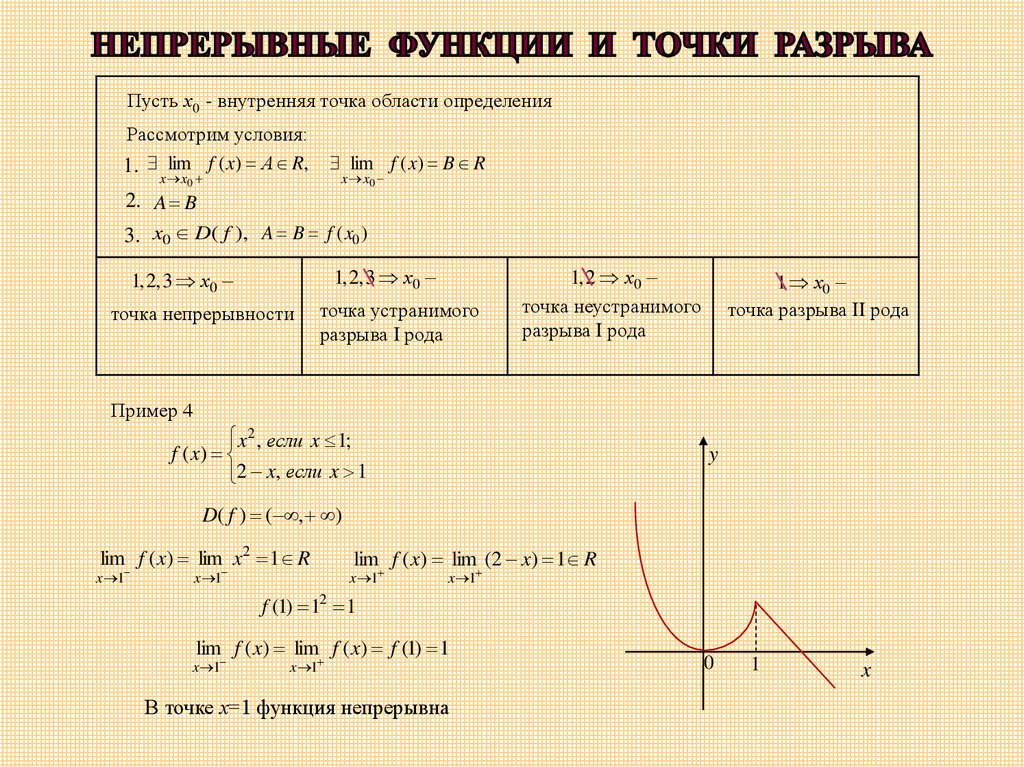
Пример 4
x 2 , если x 1;
f ( x)
2 x, если x 1
y
D( f ) ( , )
lim f ( x) lim x 2 1 R
x 1
x 1
lim f ( x) lim (2 x) 1 R
x 1
x 1
f (1) 12 1
lim f ( x) lim f ( x) f (1) 1
x 1
x 1
В точке х=1 функция непрерывна
0
1
x

9.

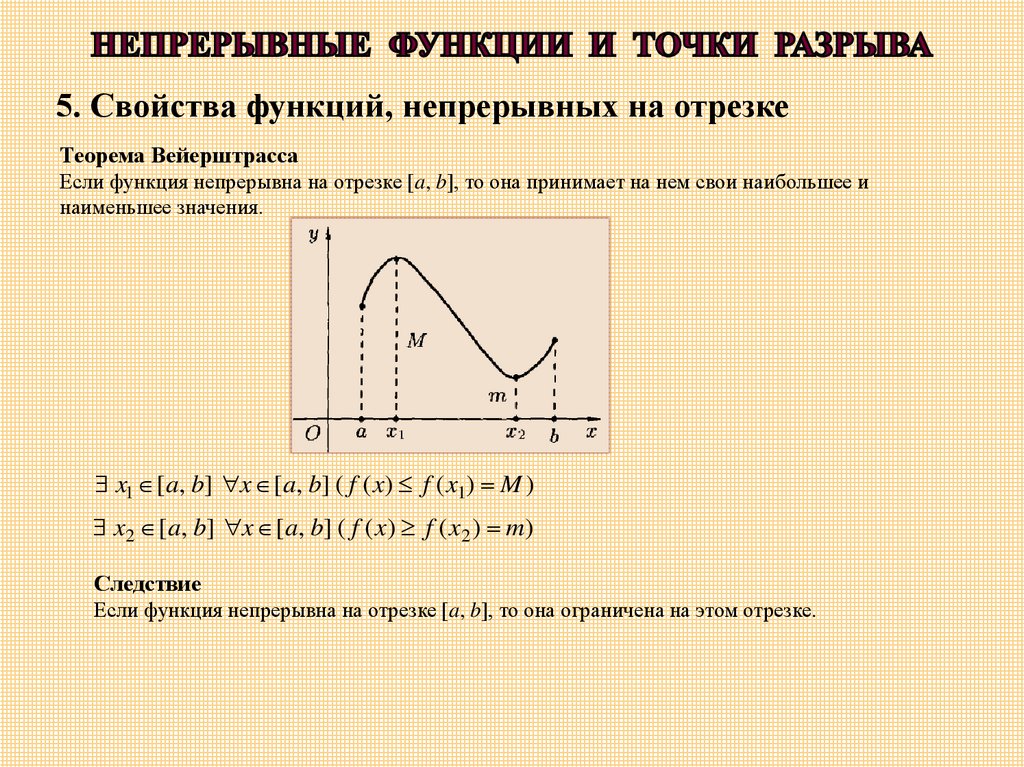
5. Свойства функций, непрерывных на отрезке
Теорема Вейерштрасса
Если функция непрерывна на отрезке [a, b], то она принимает на нем свои наибольшее и
наименьшее значения.
x1 [a, b] x [a, b] ( f ( x) f ( x1) M )
x2 [a, b] x [a, b] ( f ( x) f ( x 2 ) m)
Следствие
Если функция непрерывна на отрезке [a, b], то она ограничена на этом отрезке.

10.

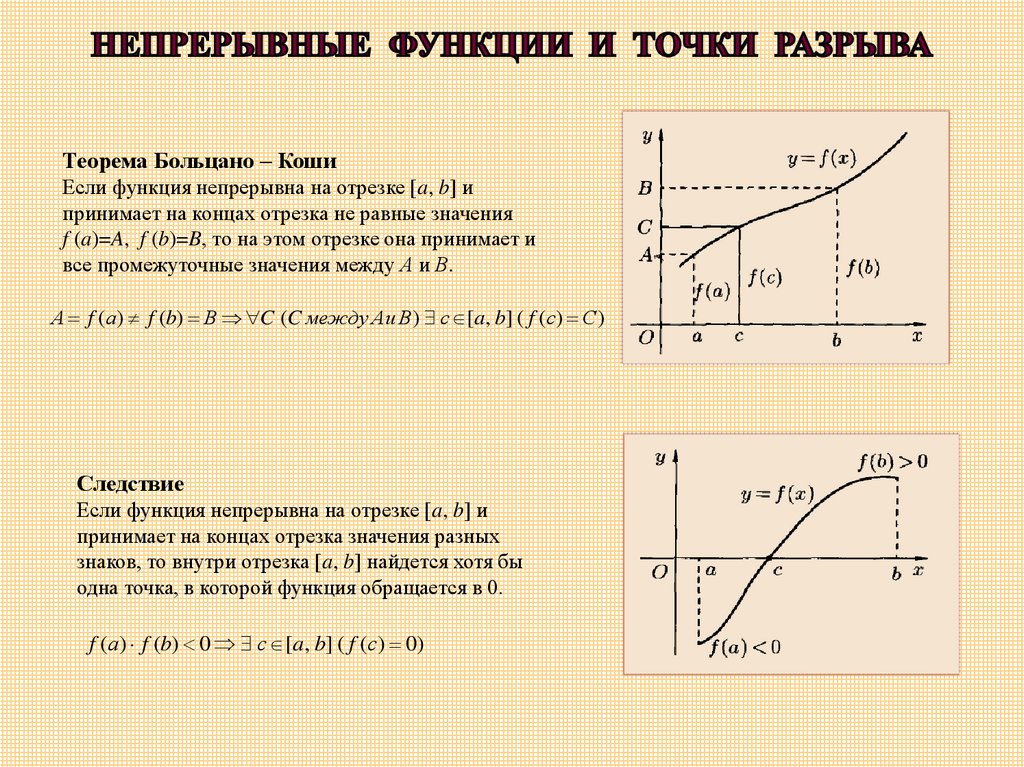
Теорема Больцано – Коши
Если функция непрерывна на отрезке [a, b] и
принимает на концах отрезка не равные значения
f (a)=A, f (b)=B, то на этом отрезке она принимает и
все промежуточные значения между А и В.
А f (а) f (b) В C (C между Аи В) с [a, b] ( f (с) С )
Следствие
Если функция непрерывна на отрезке [a, b] и
принимает на концах отрезка значения разных
знаков, то внутри отрезка [a, b] найдется хотя бы
одна точка, в которой функция обращается в 0.
f (а) f (b) 0 с [a, b] ( f (с) 0)

11.

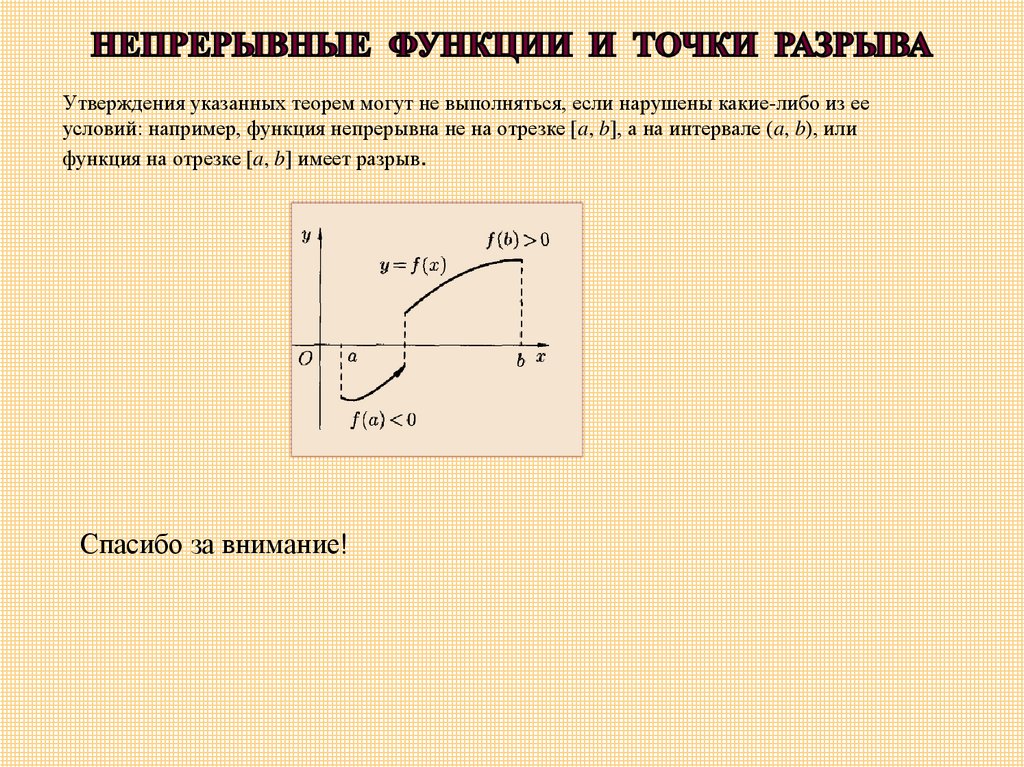
Утверждения указанных теорем могут не выполняться, если нарушены какие-либо из ее
условий: например, функция непрерывна не на отрезке [a, b], а на интервале (a, b), или
функция на отрезке [a, b] имеет разрыв.
Спасибо за внимание!