Хорда әдісі. Жанамалар (Ньютон) әдісі

1.

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
М.ӘУЕЗОВ АТЫНДАҒЫ ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ
«АҚПАРАТТЫҚ ЖҮЙЕЛЕР» КАФЕДРАСЫ
ПРЕЗЕНТАЦИЯ
ТАҚЫРЫБЫ: .
.
Орындаған: Айдынбекова Аружан
Қабылдаған : Қожабекова П

2.

ЖОСПАР:
1. Хорда әдісі.
2. Жанамалар (Ньютон) әдісі.

3.

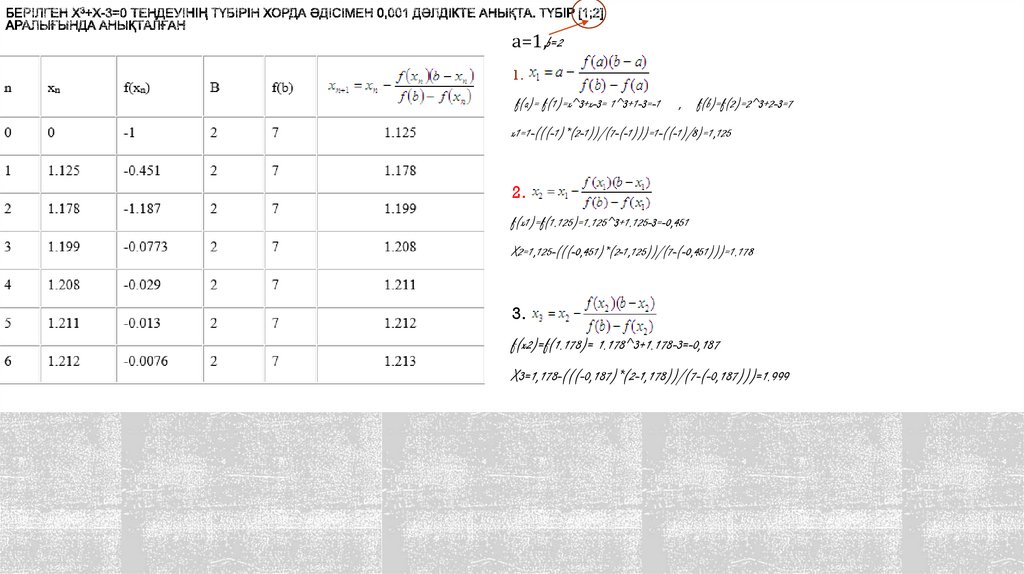
а=1,b=2
1.
=1-
f(a)= f(1)=x^3+x-3= 1^3+1-3=-1
, f(b)=f(2)=2^3+2-3=7
x1=1-(((-1)*(2-1))/(7-(-1)))=1-((-1)/8)=1,125
2.
f(x1)=f(1.125)=1.125^3+1.125-3=-0,451
X2=1,125-(((-0,451)*(2-1,125))/(7-(-0,451)))=1.178
3.
f(x2)=f(1.178)= 1.178^3+1.178-3=-0,187
X3=1,178-(((-0,187)*(2-1,178))/(7-(-0,187)))=1.999

4.

4.
xn 1 xn , n 1, 2, 3, ...болғанда тоқтатамыз, мұнда 0 қандай да бір аз шама.
x6- x5 = 1.213-1.212 = 0.001 =ε
Жауабы: x = 1.213

5.

ФОРМУЛАЛАР:
Жанамалар (Ньютон) әдісі.
Мысал:
Берілген х3-6х2+9х-3=0 теңдеуінің түбірін 0,001
дәлдікте жанама әдісімен анықта. Түбір [3; 4]
аралығында орналасқан.
n
xn
f(xn)
f1(xn)
0
4
1
9
3.889
1
3.889
0.073
7.705
3.880
2
3.880
0.002
8.603
3.880
3
3.880

6.

’
f’(x) = 3x2-12x+9 f (3,5) > 0
’’
f’’(x) = 6х – 12 f (3,5) > 0
х3 – x2 = 3.880 - 3.880 = 0
Жауабы: х=3,880