Көптік сызықтық регрессия теңдеуі

1.

Көптік сызықтық регрессия теңдеуі
Көптік сызықтық регрессия теңдеуі мынандай болады:
^
  = + + +…+
  - белгісіз параметрлер, оларды байқаудан алынған
мағлұматтардың көмегі арқылы төмендегі сызықтық тендеулер системасының
шешімі ретінде анықталады.
na b1 x1 b2 x2 ... b p x p y
2
a x1 b1 x1 b2 x1 x2 ... b p x1 x p yx1
............................................................................
a x p b1 x1 x p b2 x2 x p ... b p x 2p yx p
Мұнда
 
арқылы    
белгіленген
Сызықтық теңдеулер системасын белгілі әдістердің (Крамер, Гаусс)
бірімен шешіп регрессия теңдеуінің белгісіз параметрлерін табады.

2.

Көптік сызықтық регрессия теңдеуінің парметрлерін
басқаша да есептеуге болады. Оны кейде β әдісі деп атайды.
Мынандай түрлендірулер қарастыралық.
 
− ´
− ´
=
; =
 
Сонда регрессия теңдеуі мынандай қалыпты түрге келеді
 
Мұндағы β1, β2,…,βk – регрессияның қалыпты коэффициенттері деп аталады,
ty, tx1, tx2,…,txk – қалыпты айнымалылар деп аталады.
β1, β2,…,βk коэффициенттері төмедегі алгебралық теңдеулер системасын шешу
арқылы табылады
1 2 rx1 x 2 3rx1 x3 ... p rx1 x p rx1 y
r r ... r
2
3 x 2 x3
p x 2 x p rx 2 y
1 x 2 x1
...........................................................
1rx p x1 2 rx p x 2 3rx p x3 ... p rx p y

3.

Қалыпты, қалыпты емес регрессия коэффициенттерінің арасында байланыс бар:
  = ∙
Осы формула қалыпты регрессия теңдеуінен қалыпты емес регрессия теңдеуіне
көшуге мүмкіндік береді. Тек бос мүше мына формуламен анықталады
´ − ´ − ´ +…+ ´
=
 
Қалыпты регрессия коэффициенттерінің экономикалық мағынасы бар.
Қалыпты регрессия коэффициенті, яғни коэффициенті үлкен бола берсе
сәйкес тәуелсіз фактор мен қорытынды фактордың арасындағы байланыс
тығыздала береді. Осы жағдайды факторларды іріктеу үшін қолдануға
болады. Яғни көптік сызықтық регрессия моделінен қалыпты коэффициенті
(β- коэффициенті) өте аз болатын факторларды шығарып тастау керек.

4.

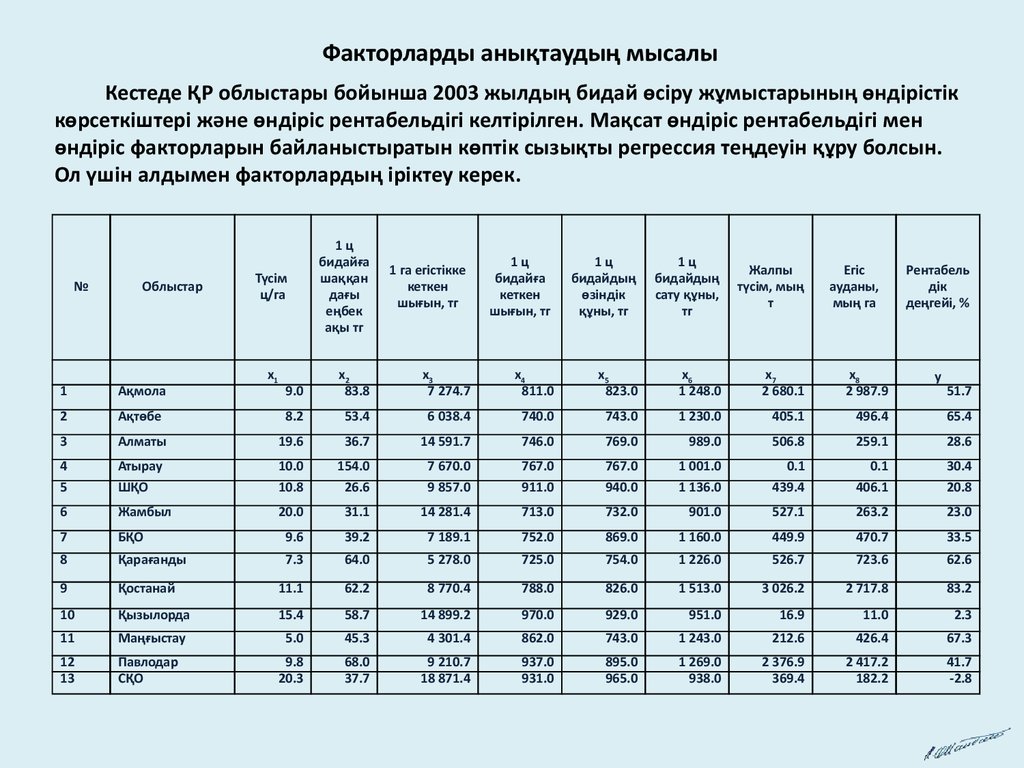
Факторларды анықтаудың мысалы
Кестеде ҚР облыстары бойынша 2003 жылдың бидай өсiру жұмыстарының өндiрiстiк
көрсеткiштерi және өндiрiс рентабельдiгi келтiрiлген. Мақсат өндiрiс рентабельдiгi мен
өндiрiс факторларын байланыстыратын көптік сызықты регрессия теңдеуiн құру болсын.
Ол үшін алдымен факторлардың іріктеу керек.
№
Облыстар
Түсім
ц/га
х1
1ц
бидайға
шаққан
дағы
еңбек
ақы тг
1 га егістікке
кеткен
шығын, тг
1ц
бидайға
кеткен
шығын, тг
1ц
бидайдың
өзіндік
құны, тг
1ц
бидайдың
сату құны,
тг
Жалпы
түсім, мың
т
Егіс
ауданы,
мың га
Рентабель
дік
деңгейі, %
1
Ақмола
9.0
х2
83.8
х3
7 274.7
х4
811.0
х5
823.0
х6
1 248.0
х7
2 680.1
х8
2 987.9
2
Ақтөбе
8.2
53.4
6 038.4
740.0
743.0
1 230.0
405.1
496.4
65.4
3
Алматы
19.6
36.7
14 591.7
746.0
769.0
989.0
506.8
259.1
28.6
4
5
Атырау
ШҚО
10.0
10.8
154.0
26.6
7 670.0
9 857.0
767.0
911.0
767.0
940.0
1 001.0
1 136.0
0.1
439.4
0.1
406.1
30.4
20.8
6
Жамбыл
20.0
31.1
14 281.4
713.0
732.0
901.0
527.1
263.2
23.0
7
БҚО
9.6
39.2
7 189.1
752.0
869.0
1 160.0
449.9
470.7
33.5
8
Қарағанды
7.3
64.0
5 278.0
725.0
754.0
1 226.0
526.7
723.6
62.6
9
Қостанай
11.1
62.2
8 770.4
788.0
826.0
1 513.0
3 026.2
2 717.8
83.2
10
Қызылорда
15.4
58.7
14 899.2
970.0
929.0
951.0
16.9
11.0
2.3
11
Маңғыстау
5.0
45.3
4 301.4
862.0
743.0
1 243.0
212.6
426.4
67.3
12
13
Павлодар
СҚО
9.8
20.3
68.0
37.7
9 210.7
18 871.4
937.0
931.0
895.0
965.0
1 269.0
938.0
2 376.9
369.4
2 417.2
182.2
41.7
-2.8
у
51.7

5.

Ол үшін төмендегі кестені құрамыз (корреляциялық матрица).
х1
х2
х3
х4
х5
х6
х7
х8
у
х1
1.000
х2
-0.334
1.000
х3
0.954
-0.328
1.000
х4
0.077
-0.119
0.356
1.000
х5
0.251
-0.224
0.488
0.808
1.000
х6
-0.700
0.064
-0.683
-0.090
-0.122
1.000
х7
-0.183
0.104
-0.179
0.042
0.091
0.707
1.000
х8
-0.319
0.154
-0.300
0.055
0.063
0.745
0.983
1.000
у
-0.703
0.148
-0.796
-0.454
-0.591
0.869
0.496
0.545
1.000
Ескерту. Кестені құру үшін MS Excel дегі «Данные-Анализ даңых-Корреляция» қондырғысын
қолдануға болады.
Енді кестеге қарасақ үш ұядағы сандар (кестеде сұр бояумен боялған)
сандар 0.7 ден көп, демек оларға сәйкес келетін факторлардың арасында
тығыз байланыс бар, яғни х1 пен х3 тің, х4 пен х5 тің, х7 мен х8 дің арасындағы
байланыстар тығыз, сондықтан олардың ішінен тек қана у пен арасындағы
байланысы тығызырағын қалдырамыз. Яғни х3, х5, х8 факторларын қалдырып
х1, х4, х7 факторларын модельден шығарамыз.

6.

Осыдан кейiн қалған x2, x3, x5, x6 және x8 факторлардың
нәтижелiк у көрсеткiшімен корреляциялық байланысы мәндi және
барлық бас жиынтық үшiн тиянақты деген мағынада тексерiлетiн
нөлдiк гипотезаны тексереміз. Ол үшiн Стьюденттiң t-критериiн
қолданамыз. Алғашқы сынақ жиынының бақылау саны n<30
болғандықтан, t-критериi мынадай формуламен есептелiнедi:
 
tр r
n 2
2
1 r
Егер жұптық корреляция коэффициентiнiң осы формуламен
есептелiнген t-критериi оның ts стандарттық (кестелік) мәнiнен
үлкен немесе тең болса, онда сынақ жиындағы у және xj
корреляциялық байланысы, бас жиынтықта да тиянақты және
сенімді екенi 0,05 деңгейлiк қателiкпен, яғни 0,95 ықтималдықпен
тұжырымдалынады да, нөлдiк жорамал қабылданады.

7.

Егер корреляция коэффициентiнiң t-критериi оның
стандартты мәнiнен кiшi (tr ts) болса, онда таңдама жиын
бойынша есептелген корреляция тығыздығы бас жиын үшiн
сенiмдi емес, яғни нөлдік гипотеза қабылданбайды.
Сондықтан, алынған нәтижелер негiзiнде, бас жиынға
байланысты сенімді тұжырым жасауға болмайды, яғни
зерттеленетiн белгiлердiң корреляция мәніне, яғни
тығыздығына байланысты жасалынатын тұжырым сенімді
емес. Мұндай жағдайда сенімсіздік тудырып отырған
факторларды талдаудан алып тастайды.
Бiздiң мысалымыз үшiн 0,05 болғанда ts 2,2.

8.

үшін
t р 2 0,148
13 2
0,148
3,3536 0, 4963 ts ,
2
1 0,148
ryx3
үшін
t р 3 0,796
11
0,796
5, 4793 4,36 ts ;
2
1 0,796
ryx5
үшін
ryx6
үшін
ryx8
үшін
ryx2
11
0,59
4,1078 2, 42 ts ;
1 0,592
11
t р 6 0,868
0,868
6,6791 5,8 t s ;
2
1 0,868
t р 5 0,59
t р 8 0,544
11
0,544
3,9527 2,15 ts .
1 0,5442
Сонымен, эконометриялық модель құру барысында, әрi қарайғы
талдаудан x2 мен x8 факторларды есепке алмаймыз да, модельде тек x3,
x5, және x6 факторларын қалдырамыз.

9.

Төмендегі кестені құралық.
№
x3
x5
x6
y
1
7.27
0.82
1.25
51.70
2
6.04
0.74
1.23
65.40
3
14.59
0.77
0.99
28.60
4
7.67
0.77
1.00
30.40
5
9.86
0.94
1.14
20.80
6
14.28
0.73
0.90
23.00
7
7.19
0.87
1.16
33.50
8
5.28
0.75
1.23
62.60
9
8.77
0.83
1.51
83.20
10
14.90
0.93
0.95
2.30
11
4.30
0.74
1.24
67.30
12
9.21
0.90
1.27
41.70
13
18.87
0.97
0.94
-2.80
Орта мәні
9.86
0.83
1.14
39.05
x 23
x 25
x 26
y2
52.92
0.68
1.56
2 672.89
36.46
0.55
1.51
4 277.16
212.92
0.59
0.98
817.96
58.83
0.59
1.00
924.16
97.16
0.88
1.29
432.64
203.96
0.54
0.81
529.00
51.68
0.76
1.35
1 122.25
27.86
0.57
1.50
3 918.76
76.92
0.68
2.29
6 922.24
221.99
0.86
0.90
5.29
18.50
0.55
1.55
4 529.29
84.84
0.80
1.61
1 738.89
356.13
115.40
0.93
0.69
0.88
1.33
7.84
2 146.03

10.

Енді мына системаны құрамыз.
1 2 rx1 x 2 3rx1 x3 ... p rx1 x p rx1 y
r r ... r r
2
3 x 2 x3
p x2 x p
x2 y
1 x 2 x1
...........................................................
1rx p x1 2 rx p x 2 3rx p x3 ... p rx p y
Excel программасындағы КОРРЕЛ функциясын қолданып мына сызықтық
корреляция коэффициенттерін табамыз.
rх3х5
rх3х6
rх5х6
rх3y
rх5y
rх6y
0.488373
-0.68333
-0.12186
-0.79617
-0.59087
0.868852
Сонда сызықтық теңдеулер системасы мынандай болады.
3 0.488373 5 0.68333 6 0.79617
0.488373 3 5 0.12186 6 0.59087
0.68333 0.12186 0.868852
1
5
6

11.

Системаны Крамер ережесімен шешіп мынаны аламыз
β3=- 0.00826
β5=-0.48891
β6=0.803628
Excel дегі КОВАР функциясын қолданып төмендегі шамаларды аламыз
σ 2y
σy
620.8256
24.91637
σ2х3
σх3
18.09663
4.254014
σ2х5
σх5
0.006465
0.080408
σ2х6
σх6
0.028439
0.168638
Регрессия теңдеуінің коэффициенттерін табу үшін мына формулаларды
қолданамыз.
y
bi i
, i 1, p
xi
Бос мүшені табамыз
a y b1 x1 b2 x2 ... bp x p
Регрессия теңдеуінің түрі мынандай болады
у 29,65 – 0,0484 x3 – 151,5 x5 + 118,7 x6

12.

Матрицалық әдіс
Мынандай белгілеулер енгізелік
1 x11
1 x12
X
... ...
1 x
1n
Y
X1
X2
…
Xk
y1
x11
x21
…
xk1
y2
x12
x22
…
xk2
…
…
…
…
…
yn
x1n
x2n
…
xkn
x 21 ... xk1
x22 ... xk 2
,
... ... ...
x2 n ... xkn
1
x11
T
X
...
x
k1
1
x12
1
x13
...
xk 2
...
xk 3
... 1
... x1k
... ...
... xkn

13.

y1
y2
Y ,
...
y
n
a
b1
B .
...
b
2
Осы белгілеулерді пайдаланып төмендегі матрицалық формуладан
регрессия теңдеуінің коэффициенттері табылады
B ( X T X ) 1 ( X T Y ).
Бұл әдіспен регрессия теңдеуін тапқанда Excel электрондық таблицасын
қолданған дұрыс.
Excel де матрицаларды көбейткен кезде былай істейді:
1. Әуелі көбейту нәтиежесінде шығатын матицаның орны белгіленеді;
2. Сосын МУМНОЖ функциясы шақырылып аргументтері енгізіледі
(аргументтердің орнын ауыстыруға болмайды);
3. Содан кейін ctrl+shipt+enter кнопкаларын осы ретпен басады№

14.

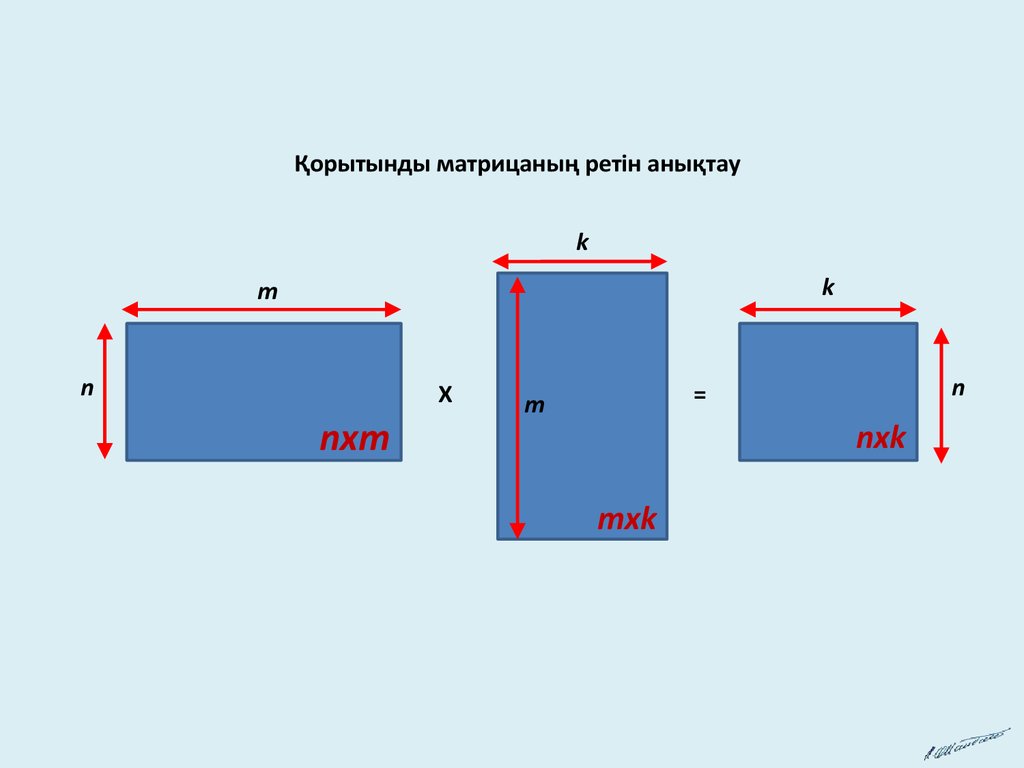
Қорытынды матрицаның ретін анықтау
k
k
m
n
Х
n
=
m
nxm
nxk
mxk