Похожие презентации:
Лекция 8. Аналитическая механика. Теорема Эмми Нётер
1. АНАЛИТИЧЕСКАЯ МЕХАНИКА
ЛЕКЦИЯ 8:ТЕОРЕМА ЭММИ НЁТЕР
2. 1. ЗАМЕНА ПЕРЕМЕННЫХ
Механическая система определена функцией Лагранжа L q, q, tЗамена переменных t , q tˆ, qˆ
Решения q(t ) системы уравнений Лагранжа с функцией L q, q, t преобразуются в решения qˆ (tˆ) системы уравнений Лагранжа с функцией Lˆ qˆ , qˆ , tˆ
dt
Lˆ tˆ, qˆ , qˆ L t , q, q
dtˆ tˆ,qˆ
t tˆ ,qˆ t (tˆ, qˆ )
qi tˆ,qˆ qi (tˆ, qˆ )
dt
t (tˆ, qˆ ) n t (tˆ, qˆ )
qˆk
ˆ
ˆ
dt tˆ,qˆ
t
qˆk
j 1
dqi
dt
tˆ , qˆ
qi (tˆ, qˆ ) n qi (tˆ, qˆ )
qˆk
tˆ
qˆk
j 1
t (tˆ, qˆ ) n t (tˆ, qˆ )
qˆk
ˆ
t
qˆk
j 1
3. 2. ПРЕОБРАЗОВАНИЕ ВАРИАЦИОННОЙ СИММЕТРИИ
Преобразование вариационной симметрии в системе с функциейЛагранжа L q, q, t - неособое преобразование t , q tˆ, qˆ расширенного координатного пространства, удовлетворяющее условию
Снята шляпа!
dt
ˆ
ˆ
ˆ
L t , q, q L t , q, q
dtˆ
Снятие шляпы означает, что qˆ (tˆ) является решением той-же самой
системы, что и q(t )
Преобразование симметрии в уравнениях Лагранжа –неособое
преобразование t , q tˆ, qˆ расширенного координатного
пространства, поточечно переводящее каждое решение q(t ) в рещение qˆ (tˆ)
той же системы.
Преобразование вариационной симметрии есть преобразование симметрии.
Есть симметрии отличные от вариационной
4. 3. ДРУГИЕ ПРЕОБРАЗОВАНИЯ СИММЕТРИИ
Дивергентные симметрии: такие, для которых выполняется условиеˆ, qˆ )
df
(
t
dt
ˆ
ˆ
ˆ
L t , q, q
L t , q, q
ˆ
dt
dtˆ
Добавление к лагранжиану полной производной от функции, зависящей
от обобщенных координат и времени не изменяет систему уравнений
Лагранжа принцип Гамильтона для L и L df dt записывается
одинаково
t1
t1
df (t , q)
t L dt dt t Ldt f (tˆ1, qˆ1 ) f (tˆ0 , qˆ0 )
0
0
число
Конформные симметрии: такие, для которых выполняется условие
dt
L tˆ, qˆ , qˆ C L t , q, q , C const
dtˆ
Следствие однородности системы уравнений Лагранжа
5. 4. ФОРМУЛИРОВКА ТЕОРЕМЫ ЭММИ НЁТЕР
Пусть материальная система описывается лагранжианом L и пусть существуетоднопараметрическое семейство преобразований вариационной симметрии
tˆ tˆ t , q; , qˆ qˆ t , q;
тождественных при 0
tˆ t , q;0 t , qˆ t , q;0 q
Тогда у системы есть первый интеграл
tˆ
qˆi
(q, p, t ) pi
H
i 1
0
0
n
n
L
pi
, H t , q, p pi qi L t , q, q
qi
i 1
6. 5. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ЭММИ НЁТЕР
qqˆ
q1
tˆ tˆ t , q;
q(t )
t
q0
t0
число
qˆ qˆ t , q;
t1
q(t ) - прямой путь ˆ
t1
t1
1
1
0
tˆ1 ( ), qˆ1 ( )
tˆ0 ( ), qˆ 0 ( )
tˆ tˆ(t , q(t ), ), qˆ qˆ (t , q(t ), )
tˆ1
tˆ
dW
dt ˆ
W
d 0
dt L tˆ, qˆ , qˆ dtˆ
ˆ
d
dt
tˆ0
tˆ0
t0
1
n
t1 n d L L
Вычисляем W pˆ i qˆi Hˆ tˆ
qˆi dtˆ при 0
i 1
0 t0 i 1 dtˆ qˆi qˆi
pˆ 1
p(t1 ), Hˆ
H (t1 , q (t1 ), p (t1 ))
W L t , q, q dt L t , q, q tˆ,qˆ
tˆ 1
0
0
1 0
tˆ(t1 , q(t1 ), )
d
0
qˆi (t1 , q(t1 ), )
d
0
qˆi 1 0
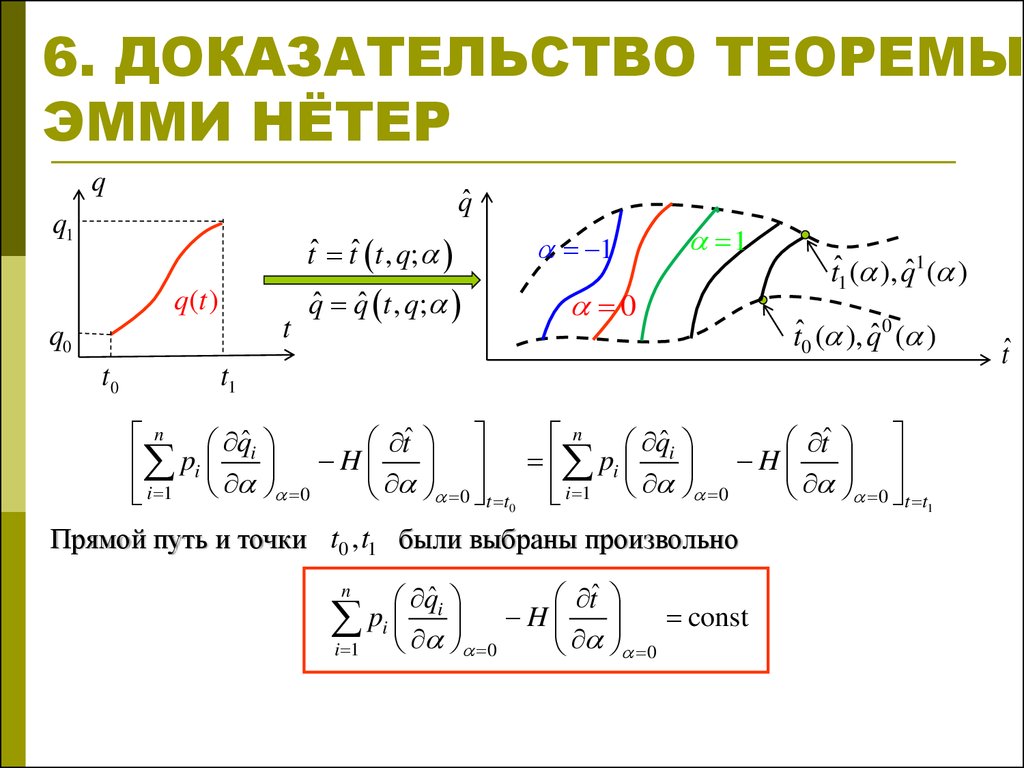
7. 6. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ЭММИ НЁТЕР
qqˆ
q1
tˆ tˆ t , q;
q(t )
t
q0
t0
qˆ qˆ t , q;
1
1
0
tˆ1 ( ), qˆ1 ( )
tˆ0 ( ), qˆ 0 ( )
t1
n qˆi
n qˆi
tˆ
tˆ
pi
pi
H
H
0
0
i 1
0 t t0 i 1
0 t t1
Прямой путь и точки t0 , t1 были выбраны произвольно
tˆ
qˆi
pi H const
0
i 1
0
n
tˆ
8. 7. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Обобщенно консервативная системаL L(q, q)
Однопараметрическое семейство преобразований
qˆi qi , tˆ t
Условие вариационной
симметрии
L q, q dt L qˆ, qˆ dtˆ
dtˆ
1,
dt
dqˆ dq
ˆ
dt dt
tˆ
qˆi
(q, p, t ) pi
H
H
0
i 1
0
n
H const
Закон сохранения энергии – следствие инвариантности лагранжиана
системы относительно сдвига по времени
9. 8. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА ДЛЯ ЦИКЛИЧЕСКИХ КООРДИНАТ
L L(t , q2 ,Система с циклической координатой q1
Однопараметрическое семейство преобразований
tˆ t , qˆ1 q1 , qˆi qi (i 2, , n)
Условие вариационной
симметрии
L q, q dt L qˆ, qˆ dtˆ
, qn , q1 ,
, qn )
dqˆ1 dq
ˆ
dt
dt
tˆ
qˆi
(q, p, t ) pi
p1
H
0
i 1
0
n
p1 const
Закон сохранения импульса для циклической координаты – следствие
инвариантности лагранжиана системы относительно сдвига по этой
координате
10. 9. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
Замкнутая система n материальных точек. Потенциальная энергиявзаимодействия точек зависит только от расстояния между ними.
(rik ), rik2 ri rk xi xk yi yk zi zk
1 n
2
2
2 2
L T mi xi yi zi rik
2 i 1
Однопараметрическое семейство преобразований
dxˆi dxi
tˆ t , xˆi xi , yˆi yi ,
zˆi zi
,
ˆ
dt
dt
Условие вариационной
L q, q dt L qˆ, qˆ dtˆ
( xˆi xˆk ) ( xi xk )
симметрии
2
2
2
2
n
n
tˆ
xˆi
yˆi
zˆi
p x ,i
px ,i mi xi
p y ,i
pz ,i
H
0
0
0
i 1
i 1
0 i 1
n
n
Qx mi xi const
i 1
Закон сохранения количества движения– следствие инвариантности
лагранжиана системы относительно сдвига по пространственной координате
11. 10. ЗАКОН СОХРАНЕНИЯ КИНЕТИЧЕСКОГО МОМЕНТА
Замкнутая система n материальных точек. L 1 m x y z2
n
i 1
i
2
i
2
i
Однопараметрическое семейство преобразований
tˆ t , xˆi xi cos yi sin , yˆi xi sin yi cos ,
2
2
2 2
i
zˆi zi
2
2
rik
rˆik2 rik2
2
dyi
dyi
dxˆi dyˆi dxi
dxi
dxi dyi
cos
sin
sin
cos
ˆ ˆ
dt
dt
dt
dt
dt
dt
dt
dt
Условие вариационной симметрии выполнено
n
xˆi
yˆi
zˆi
tˆ
px ,i
p y ,i
p z ,i
H
0
0
0
i 1
px ,i yi p y ,i xi
n
0
2
i 1
n
K z mi xi yi yi xi const
i 1
Закон сохранения кинетического момента– следствие инвариантности
лагранжиана системы относительно поворотов.
12. 11. ПРИМЕР В.Ф. ЖУРАВЛЕВА
1 dqL
2 dt
Свободная материальная точка
tˆ te A , qˆ qe B
Семейство преобразований
2
2
dte A 1 dq 2
1 dqˆ dtˆ 1 d qe
2 B A
ˆ
e
A
2 dt dt 2 d te
dt 2 dt
Условие вариационной симметрии выполнено при A 2 B
tˆ
1 2
qˆ
2
2
( q, p, t ) p
H
Bpq
p
At
B
pq
p
t
B
q
t
2
0
0
2
B
q q qt const











 Физика
Физика Механика
Механика








