Расчет элементов ДК по ПС (Лекция ДК №4)

1. Тема лекции: Расчет элементов ДК по 1 группе ПС (продолжение). Расчет элементов ДК по 2 группе ПС

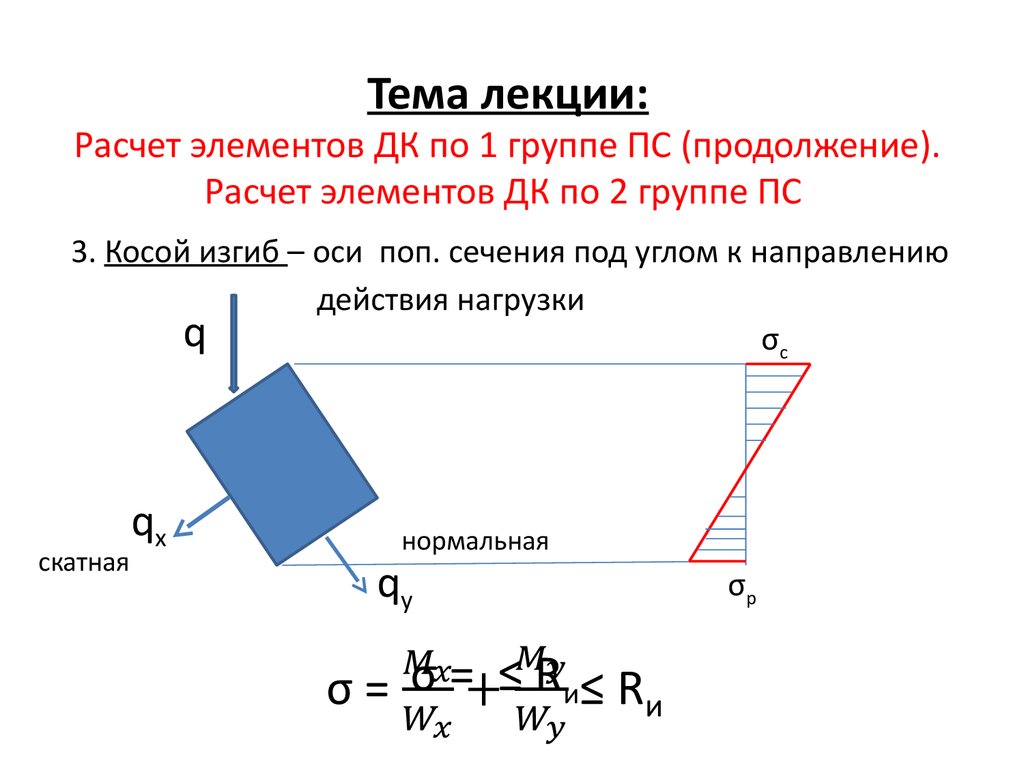
3. Косой изгиб – оси поп. сечения под углом к направлению
действия нагрузки
q
σс
скатная
qx
нормальная
qy
σ = ≤ Rи
σр

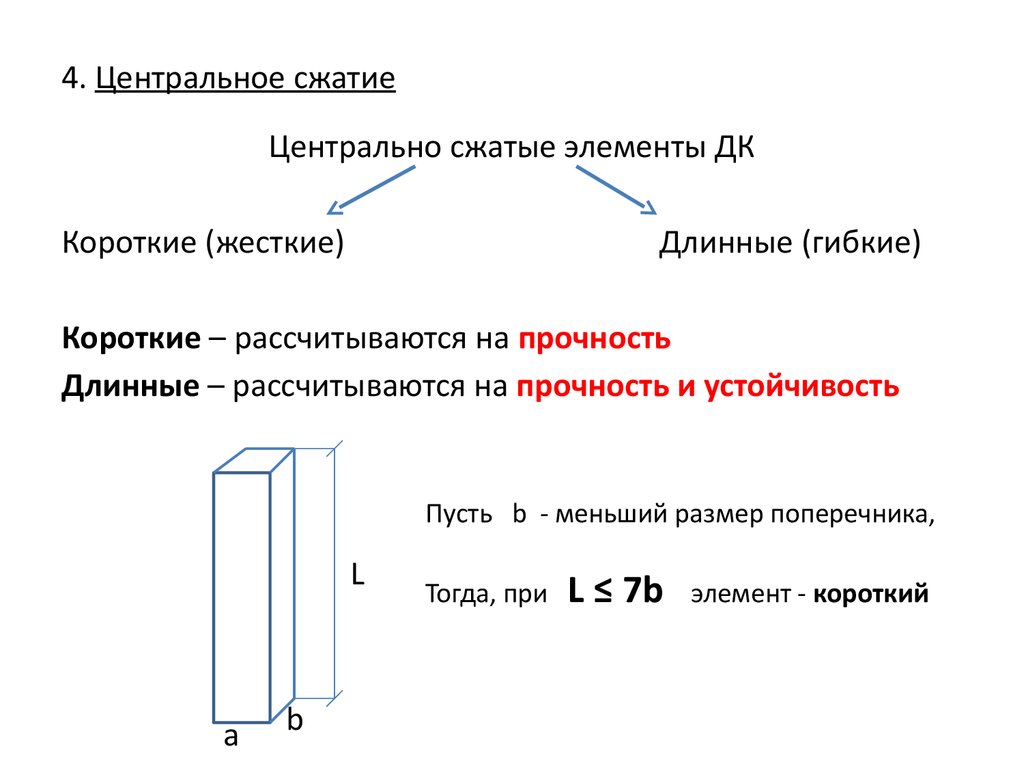
2. 4. Центральное сжатие

Центрально сжатые элементы ДК
Короткие (жесткие)
Длинные (гибкие)
Короткие – рассчитываются на прочность
Длинные – рассчитываются на прочность и устойчивость
Пусть b - меньший размер поперечника,
L
a
b
Тогда, при
L ≤ 7b
элемент - короткий

3. А. Прочность

σ = ≤ Rc
(Ант – без учета совмещения ослаблений)
Б. Устойчивость (потеря – искривление стержня, при
напряжениях σ кр меньших предела прочности σ кр = ϕ ▪ Rпч )
σ = ≤ Rc
- расчетная площадь поперечного сечения
• = если ослаблений нет, или они ≤ 25% и не на кромки
• = если внутренние ослабления > 25%
• = при симметричных наружных ослаблениях

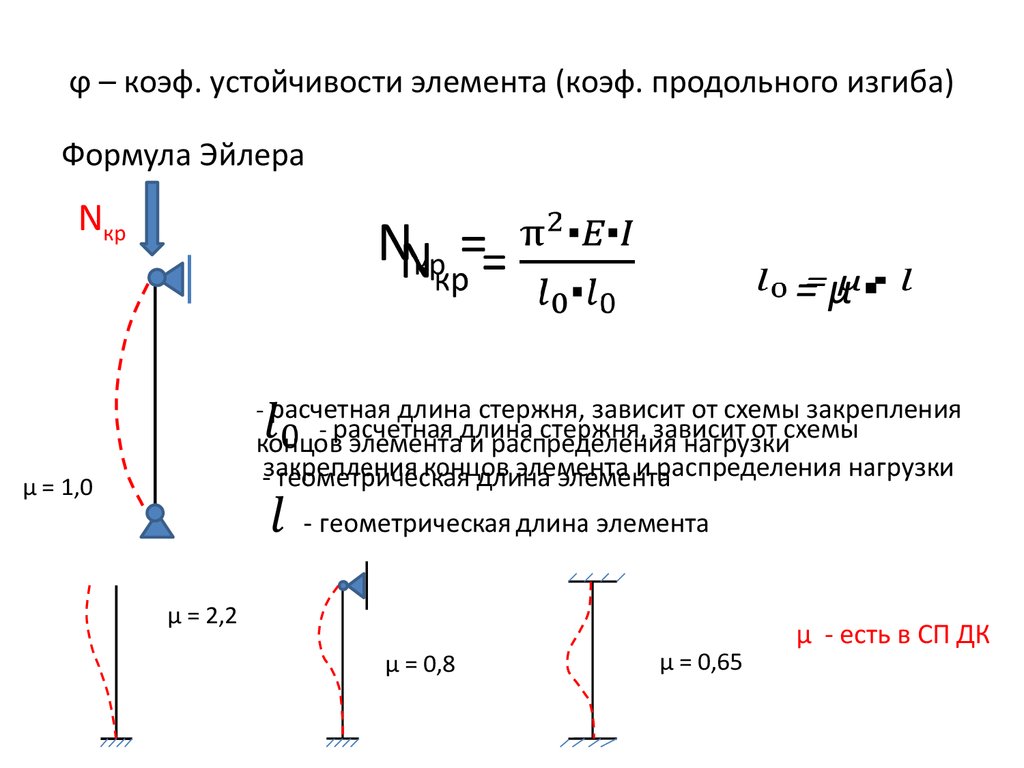
4. ϕ – коэф. устойчивости элемента (коэф. продольного изгиба)

Формула Эйлера
Nкр
Nкр =
=μ▪
- расчетная длина стержня, зависит от схемы закрепления
концов элемента и распределения нагрузки
- геометрическая длина элемента
μ = 1,0
μ = 2,2
μ = 0,8
μ = 0,65
μ - есть в СП ДК

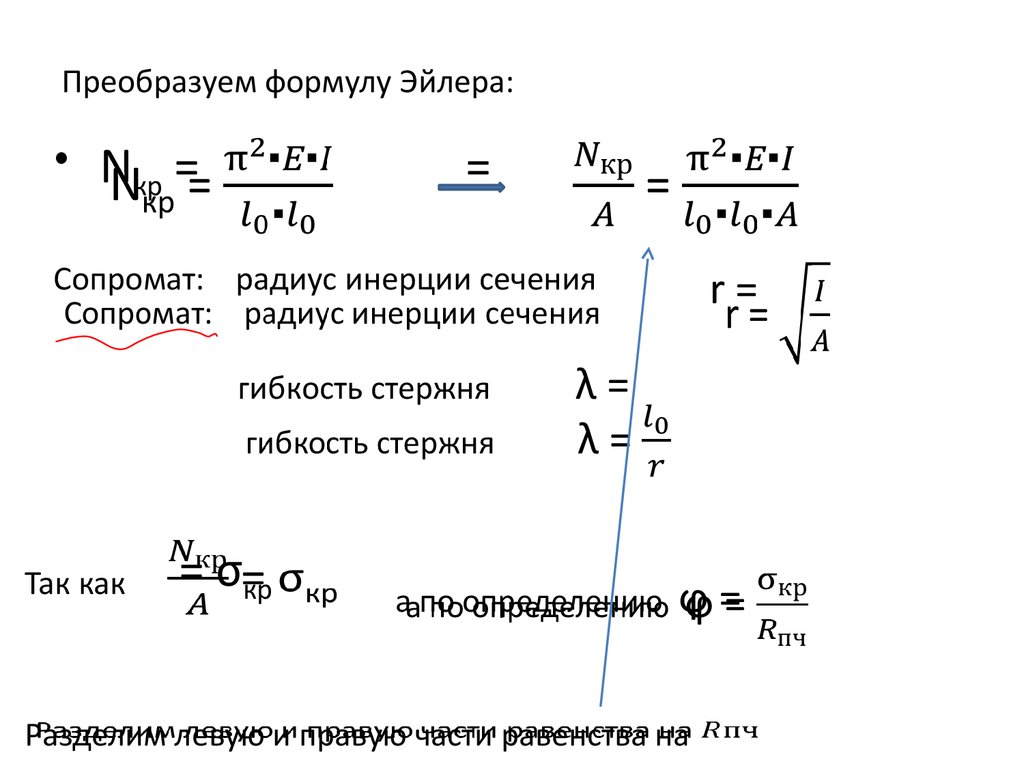
5. Преобразуем формулу Эйлера:

• Nкр =
=
Сопромат: радиус инерции сечения
гибкость стержня
Так как
= σкр
r=
λ=
а по определению
ϕ=
Разделим левую и правую части равенства на

6. выражение для коэф. продольного изгиба:

ϕ= ;
= const = K
ϕ=
Для дерева К =3000
Для фанеры К=2500
Однако, Е = const не всегда, а только до предела
пропорциональности (см. диаграмму σ
– ε)

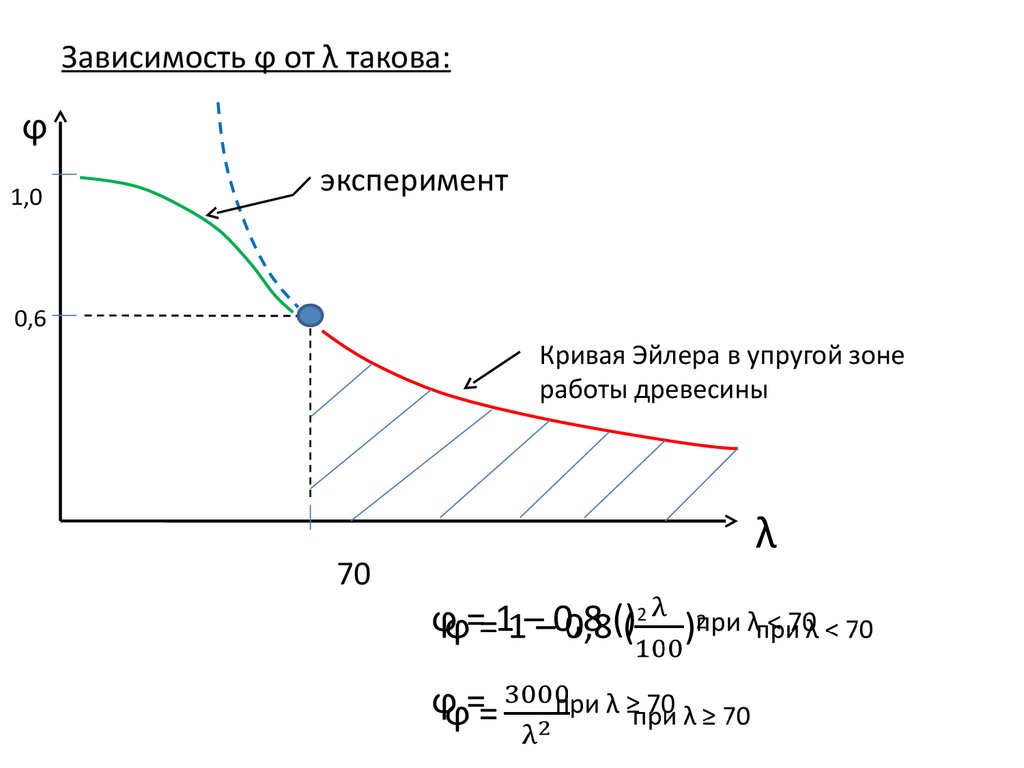
7. Зависимость ϕ от λ такова:

ϕ
1,0
эксперимент
0,6
Кривая Эйлера в упругой зоне
работы древесины
70
λ
ϕ = 1 – 0,8 ()2
ϕ=
при λ ≥ 70
при λ ˂ 70

8. Гибкость λ элементов ДК ограничена

1. Сжатые пояса, опорные раскосы и опорные стойки ферм,
колонны
λ ≤ 120
2. Прочие сжатые элементы ферм и других сквозных
конструкций
λ ≤ 150
3. Сжатые элементы связей
λ ≤ 200
4. Растянутые пояса ферм в вертикальной плоскости λ
≤ 150
5. Прочие растянутые элементы ферм и других сквозных
конструкций
λ ≤ 200

9. Порядок расчета элемента ДК на устойчивость

Дано: Rc , N , геом. длина, μ , λпр
Найти: А, b х h
1. Ищем минимально возможные размеры b х h
hmin
bmin
dmin

10. 2. Минимальные размеры обладают мин. радиусом инерции

h
b
h
b
rmin = = = 0,289 b
Для круглого сечения: rmin =
0,25d
3. Гибкость стержня по определению (сопромат):
λ = =
или
rmin =

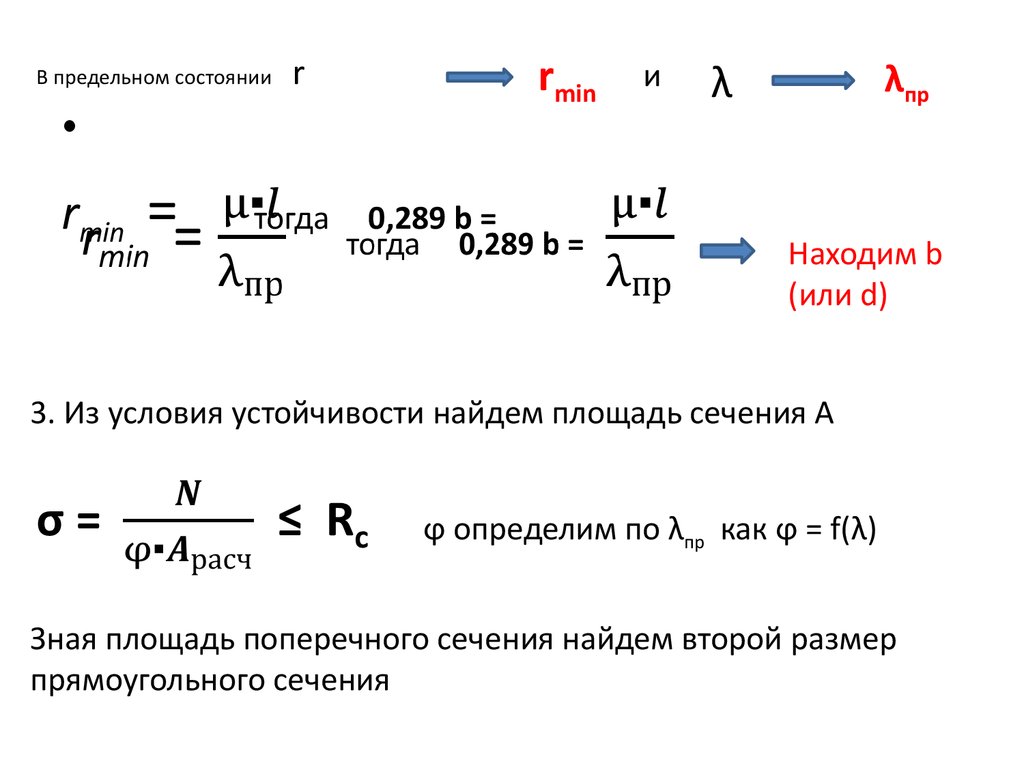
11. В предельном состоянии r

В предельном состоянии
rmin
r
rmin
=
тогда
0,289 b =
и
λпр
λ
Находим b
(или d)
3. Из условия устойчивости найдем площадь сечения A
ϕ определим по λпр как ϕ = f(λ)
Зная площадь поперечного сечения найдем второй размер
прямоугольного сечения

12. Простой пример расчета центрально сжатого элемента ДК по 1 группе ПС

Дано:
элемент – опорная стойка, с шарнирно
закрепленными (μ = 1,0) концами L = 4,5 м., не имеет
ослаблений поп. сечения, N = 27000 кг, из древесины 1 сорта
(Rс = 140 кг/см2)
Найти: минимальные размеры поперечного сечения
1. Из условия прочности найдем требуемую площадь
сечения:
А ≥ = = 192,9 см2

13. 2. Из сортамента на пиломатериалы примем квадратное поперечное сечение b x h = 150 x 150 мм

3.
• Определим характеристики сечения:
rx = 0,289h = 0,289▪15 = 4,34 см
ry = 0,289b = 0,289▪15 = 4,34 см
4. Расчетные длины стержня в плоскостях X и Y:
L0x = μ ▪ L = 1,0 ▪ 450 = 450 см
L0y = μ ▪ L = 1,0 ▪ 450 = 450 см
5. Гибкость стержня:
λ = λx = λy = = = 103,7 ˂ λпр = 120 По гибкости стержень
подходит!!!
6. Определим коэффициент устойчивости
Так как λ > 70
ϕ = 3000/λ2 = 3000/103,72 = 0,279

14. 7. Проверка условия устойчивости:

σ = ≤ Rc
σ = = 430,1 кг/см2 > Rc = 140 кг/см2
Устойчивость не обеспечивается – сечение мало !!!!
авария гарантируется!!!
Увеличиваем размеры сечения (в рамках сортамента)
Пусть сечение 200 х 200 мм
Тогда r = 0,289▪20 = 5,78 см; λ = 450/5,78 = 77,85
ϕ = 3000/77,852 = 0,49
σ = = 137,8 кг/см2 ˂ Rc = 140 кг/см2
Устойчивость обеспечена !!!

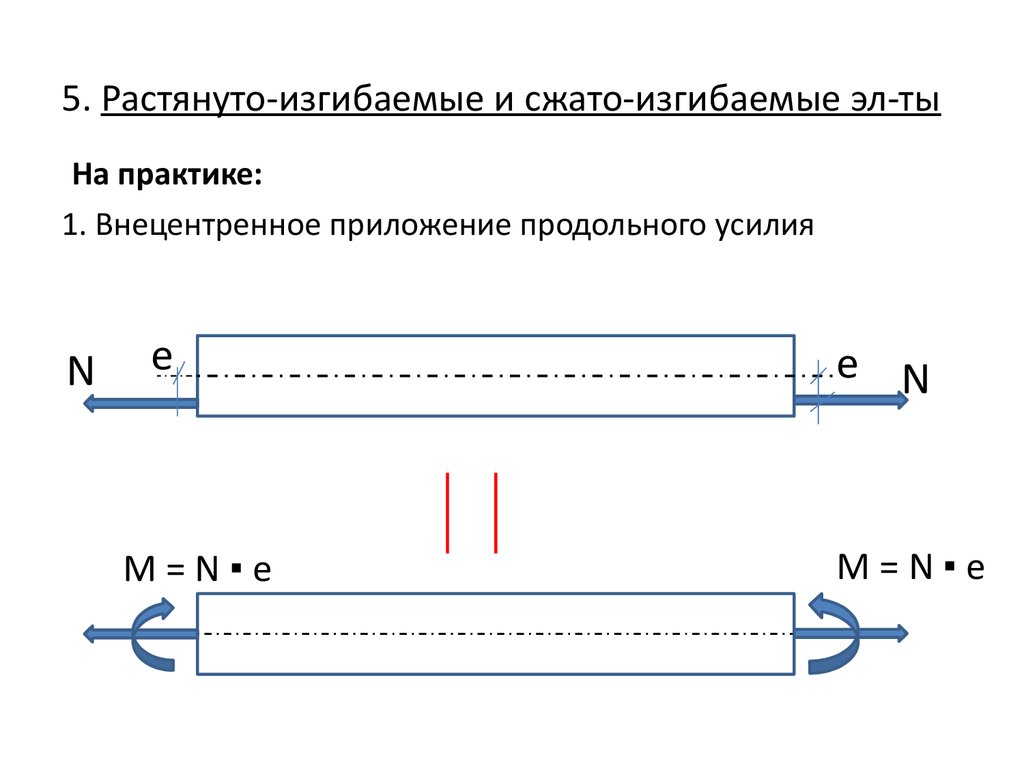
15. 5. Растянуто-изгибаемые и сжато-изгибаемые эл-ты

На практике:
1. Внецентренное приложение продольного усилия
N
e
M=N▪e
е N
M=N▪e

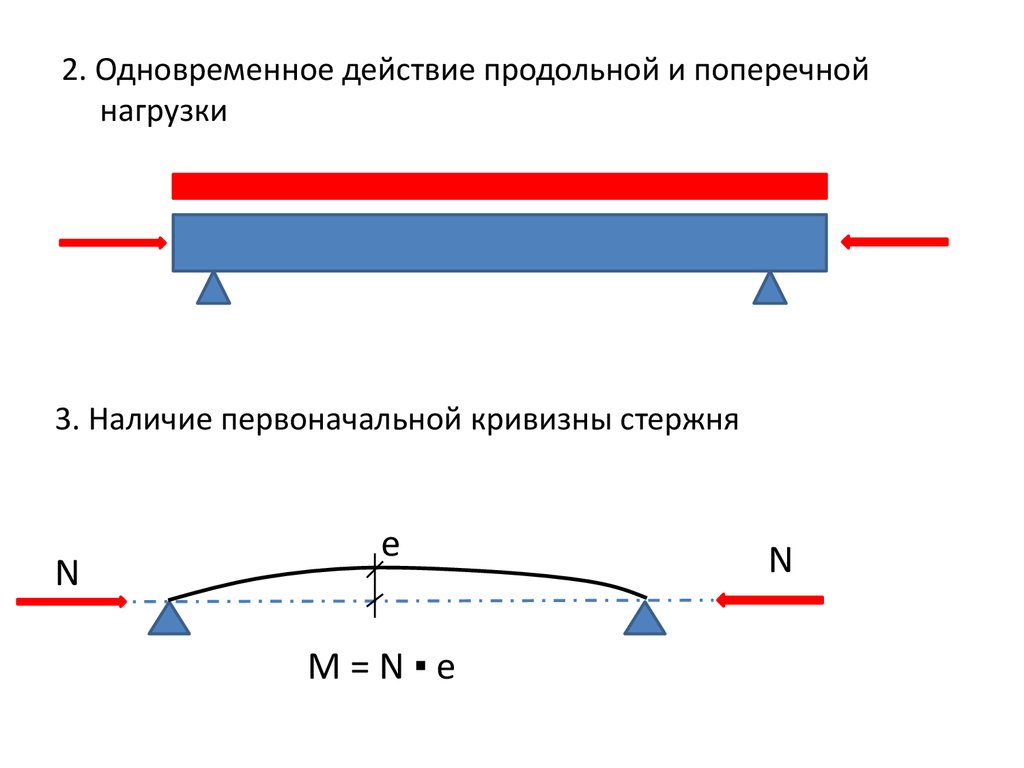
16. 2. Одновременное действие продольной и поперечной нагрузки

3. Наличие первоначальной кривизны стержня
N
е
M=N▪e
N

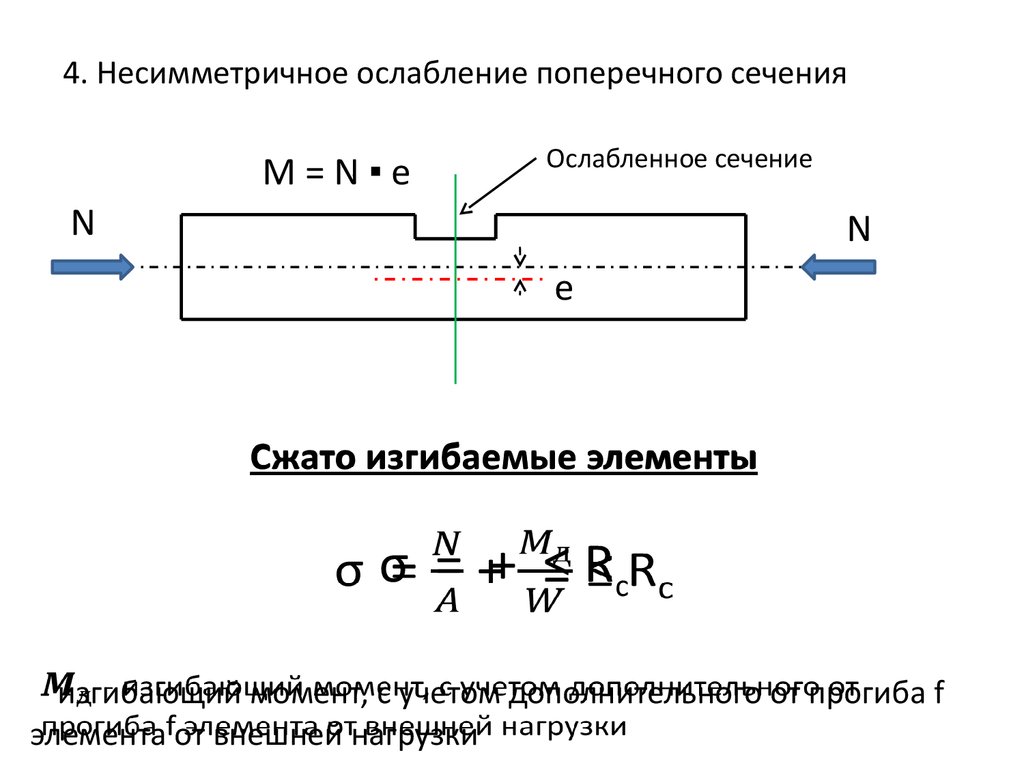
17. 4. Несимметричное ослабление поперечного сечения

M=N▪e
Ослабленное сечение
N
N
е
Сжато изгибаемые элементы
σ = + ≤ Rc
- изгибающий момент, с учетом дополнительного от прогиба f
элемента от внешней нагрузки

18. M_д = M/ξ где ξ – коэф. учитывающий дополнительный момент Mдоп = N ▪ f

= M/ξ
момент
где
ξ – коэф. учитывающий дополнительный
Mдоп = N ▪ f
ξ=1Растянуто изгибаемые элементы
σ = + ≤ Rр
Дополнительный момент Mдоп = N ▪ f не учитывается

19. Расчет элементов ДК по 2 группе ПС (на жесткость)

•Деформации ДК или их отдельных элементов следует в
общем случае определять с учетом сдвига и
податливости соединений
1. Изгиб
f0 =
f0 - прогиб без учета сдвига
k1 - учитывает вид нагрузки и опирание концов элемента (расчетнотеоретический справочник проектировщика 1960 под ред А.А Уманского)

20.

k1 =5/384
……………
f ≤ fпр
fпр - предельное значение прогиба (установлено в СП 64.13330.2011)
Элементы конструкций
1 Балки междуэтажных перекрытий
2 Балки чердачных перекрытий
3 Покрытия :
а) прогоны, стропильные ноги
б) обрешетки, настилы
fпр (в долях пролета)
1/250
1/200
1/200
1/150

21. Прогиб с учетом касательных напряжений (сдвиг):

k – учитывает переменность высоты балки
с - учет сдвига (k и c приведены в СП 64.13330.2011)
Для балки постоянного поперечного сечения и загруженной
равномерно распределенной нагрузкой: k = 1, c = 19,2
Практически, если балка постоянного сечения и ≥ 15 (т.е.
балка не высокая), тогда f0 ≤ fпр (наш курсовик)

22. 2. Косой изгиб

3. Сжатие с изгибом
fN =
f - по формулам для изгиба
ξ - учет дополнительного момента

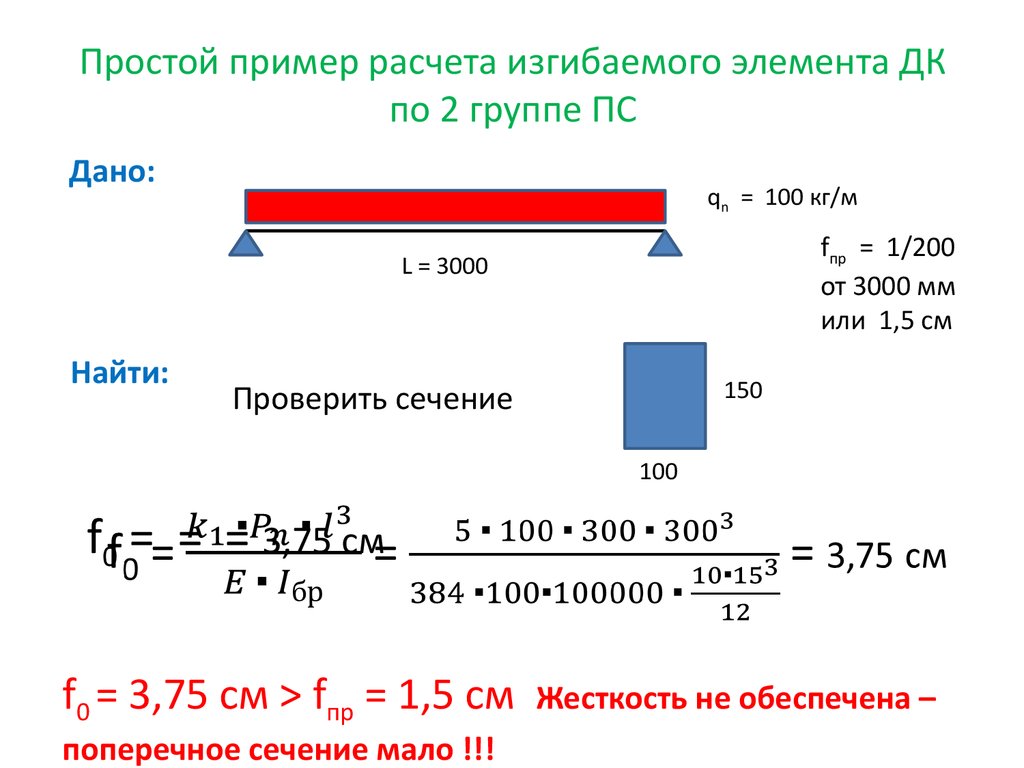
23. Простой пример расчета изгибаемого элемента ДК по 2 группе ПС

Дано:
qn = 100 кг/м
fпр = 1/200
от 3000 мм
или 1,5 см
L = 3000
Найти:
150
Проверить сечение
100
f0 = = = 3,75 см
f0 = 3,75 см > fпр = 1,5 см
поперечное сечение мало !!!
Жесткость не обеспечена –