Похожие презентации:
Прикладные пакеты компьютерной графики. Цветовые модели
1.
ПРИКЛАДНЫЕ ПАКЕТЫ КОМПЪЮТЕРНОЙ ГРАФИКИЦВЕТОВЫЕ МОДЕЛИ
Лекция №4
2. Цифровое растровое изображение
Цифровое растровое изображение представляетсобой прямоугольную матрицу единиц
изображения – пикселей
Каждый пиксель цифрового растрового
изображения имеет определенный набор атрибутов
Цвет, прозрачность и др.
3. Пример растрового изображения
4. Цвет
Цвет в цифровых изображениях кодируется припомощи чисел, задающих координаты данного
цвета в некотором цветовом пространстве
Абстрактная математическая модель,
описывающая способ представления цветов при
помощи кортежей чисел из 3 или 4 элементов
Существование различных цветовых
пространств (цветовых моделей)
обуславливается их различной применимостью
в различных областях компьютерной графики
5. Классификация цветовых моделей
Подходят для описание восприятия цвета (XYZ, L*a*b)Аддитивные модели – рецепты получения цвета на
мониторе (RGB)
Полиграфические (субтрактивные) модели –
получение цвета при использовании разных красок
(CMYK)
Модели, являющиеся стандартом передачи
информации, не связанные с оборудованием (YUV, YIQ)
Модели, полезные для каких либо способов
цветокоррекции, не связанные с оборудованием (HSV)
6. Плотность цветового пространства
Каждая цветовая модель реализовывается взависимости от возможностей используемой
системы
Например многие современные реализации
пространства RGB основываются используют 24 бита
на хранение информации о цвете. Любой цвет в таких
системах ограничен гаммой в 256*256*256=16,7 млн.
цветов
В то же время реализации использующие по 16 бит на
хранение каждой цветовой компоненты способны
передать тот же цветовой диапазон с большей
плотностью
7. Цветовая модель RGB
Это аддитивная цветовая модель, в которойцвета трех базовых источников света (красного,
зеленого и синего), смешиваясь в различных
пропорциях, образуют остальные цвета
Данная цветовая модель используется для
построения изображений на цветных
мониторах
8. Физиологический характер модели RGB
Наличие данной цветовой модели имеет скореефизиологический, нежели физический
характер, поскольку колбочки в сетчатке наших
глаз чувствительны именно к этим трем цветам
Глаза птиц, например, чувствительны к 4
базовым цветам
Глаза многих млекопитающих – к двум цветам
Свет с разными спектрами может иметь один и
тот же цветовой стимул (отклик в колбочках на
цвет определенного спектра) и будет
восприниматься человеком одинаково
При дальтонизме также возможно нарушение
восприятия цветов человеком
9.
Данная цветовая модель называется аддитивной (от англ.Addition - сложение), поскольку каждый дополнительный цвет
вносит положительный вклад в формирование финального
цвета
10. Цветовая модель CMYK
Это субтрактивная цветовая модель,используемая в цветной полиграфии
Цветовая модель основана на смешивании
пигментов следующих цветов:
C – Cyan (голубой)
M – Magenta (пурпурный)
Y – Yellow (желтый)
K – Key, blacK (черный)
11.
Данная цветовая модель основана на поглощениицвета, возникающем при смешивании базовых
цветов данной модели
При смешивании идеальных Голубого, Желтого и
Пурпурного цветов в результате получается черный
цвет
Поэтому данная цветовая модель нашла широкое
применение в полиграфии
12. Для чего нужен черный цвет в модели CMYK?
Подмешивание черного цвета при цветной печатипозволяет управлять яркостью изображения путем
меньшего количества цветной краски
Кроме того, текст обычно имеет черный цвет, что
позволяет обходиться одними черным цветом
13.
Данная цветовая модель называется субтрактивной (от англ. Subtraction- вычитание), поскольку каждый дополнительный цвет вносит
отрицательный вклад в формирование финального цвета, действуя как
дополнительный светофильтр
14. Цветовой куб
Цветовые модели RGB и CMYK образуют такназываемый цветовой куб
15. Сравнение цветовых моделей RGB и CMYK
Цвета, получаемые на мониторе зачастуюотличаются от цветов, используемых при печати
Невозможно получить чистый синий цвет модели
RGB (0, 0, 100%) в цветовом пространстве CMYK – его
ближайший эквивалент – оттенок пурпурного цвета
Цвет, получаемый на мониторе – комбинация
разноцветных цветовых источников, которая при
печати не может быть воспроизведена. Поэтому
перед печатью RGB-изображения необходимо
конвертировать его в CMYK-эквивалент
16. Сравнение цветовых пространств RGB и CMYK
http://en.wikipedia.org/wiki/Image:RGB_CMYK_4.jpg17. Преобразование RGB в CMYK
tRGB = {R, G, B}tCMY = {C’, M’, Y’}={1–R, 1–G, 1–B}
If min{C’, M’, Y’} = 1 then
tCMYK = {0, 0, 0, 1}
Else
K = min{C, M, Y}
tCMYK = {(C’–K)/(1-K), (M’-K)/(1-K), (Y’-K)/(1-K), K}
18. Преобразование CMYK в RGB
tCMYK = {C, M, Y, K}tCMY = {C’, M’, Y’} =
{C*(1-K) + K, M*(1-K) + K, Y*(1-K)+K}
tRGB = {1 – C’, 1-M’, 1-Y’}
19. Цветовая модель HSV (HSB)
Данная цветовая модель задает цветовоепространство в терминах следующих составных
компонент:
Hue – оттенок цвета (красный, синий, зеленый)
Диапазон 0-360° (0-100% в некоторых Реализациях)
Saturation – насыщенность цвета (цветовая чистота)
Диапазон от 0 до 100%. Меньшие значения насыщенности
делают цвет серым, в то время как бОльшие значения – более
«цветным»
Value (Brightness) – яркость цвета
Для многих людей такой способ задания цвета
является интуитивно более понятным, нежели
RGB или CMYK
20.
VS
H
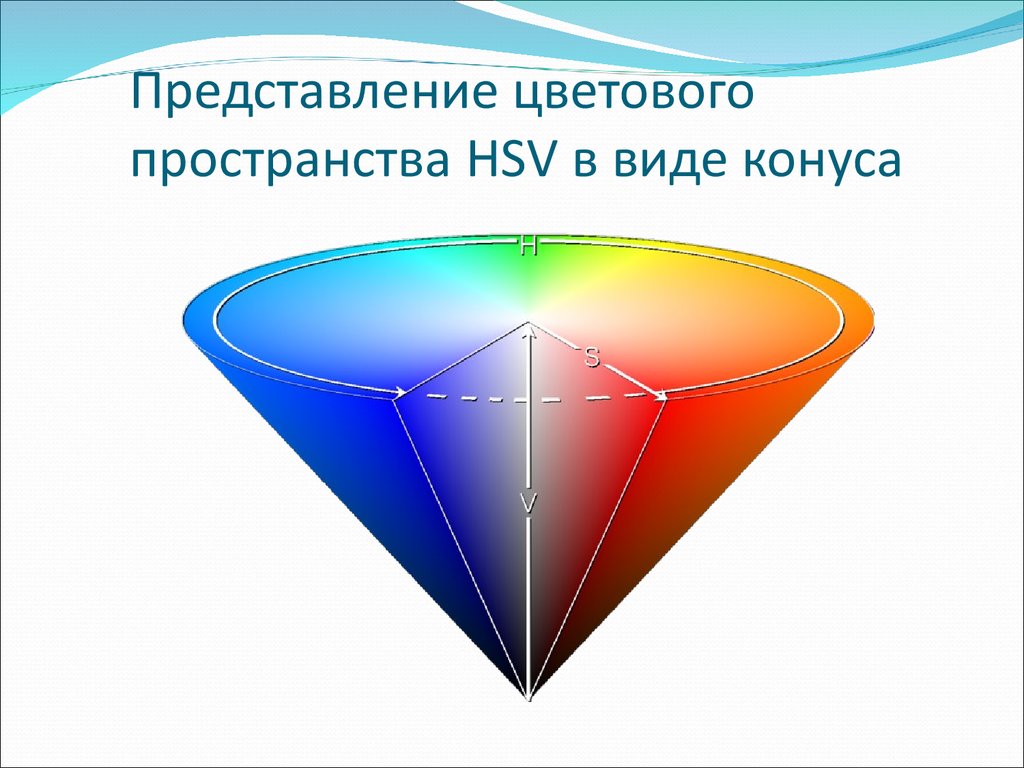
21. Представление цветового пространства HSV в виде конуса
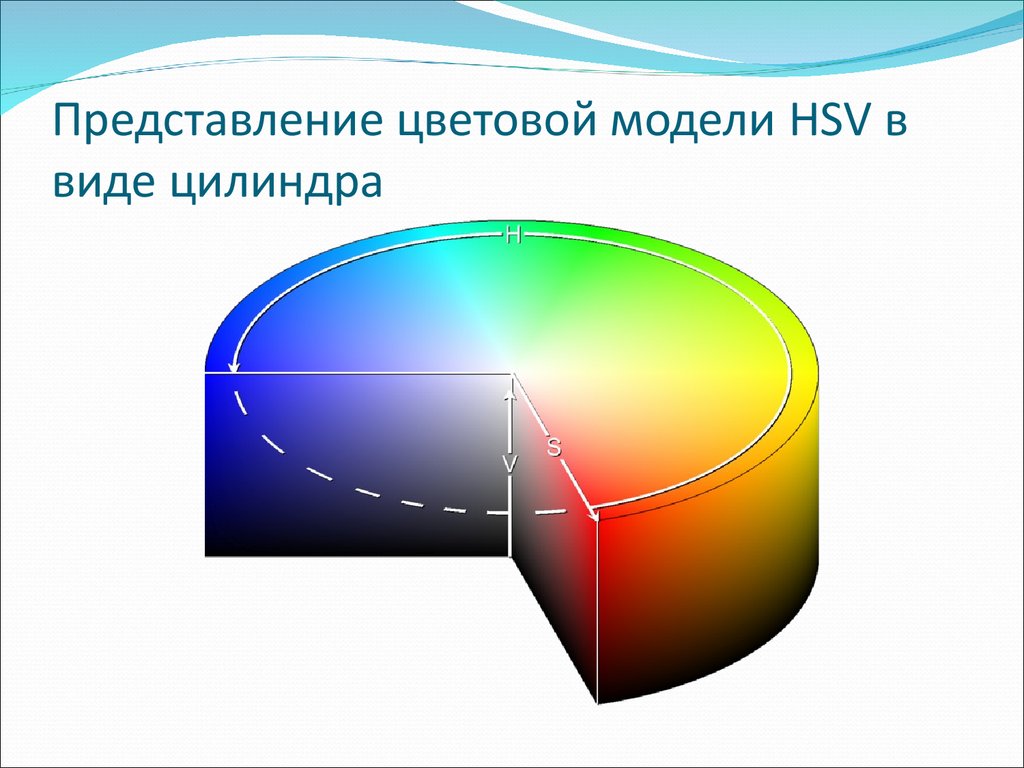
22. Представление цветовой модели HSV в виде цилиндра
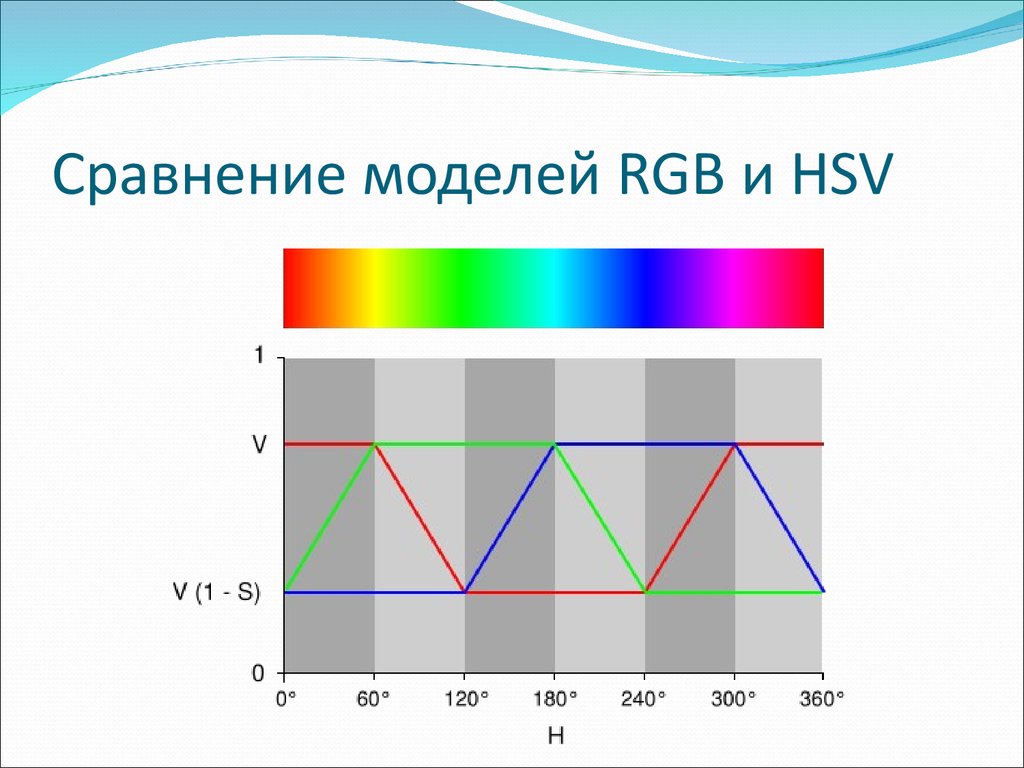
23. Сравнение моделей RGB и HSV
24. Преобразование из цветовой модели RGB в HSV
H [0, 360)S,V,R,G,B [0, 1]
MAX = max(R, G, B); MIN = min(R, G, B)
25. Преобразование из HSV в RGB
Hi=[H/60] mod 6f = H/60 – Hi
p=V*(1-S)
q=V*(1-f*S)
t=V*(1-(1-f)*S)
If Hi = 0 ->
R=V, G=t, B=p
If
If
If
If
If
Hi = 1
Hi = 2
Hi = 3
Hi = 4
Hi = 5
->
->
->
->
->
R=q,
R=p,
R=p,
R=t,
R=V,
G=V,
G=V,
G=q,
G=p,
G=p,
B=p
B=t
B=V
B=V
B=q
26. Ограничения формата HSV
Цифровые изображения обычно используют целыечисла диапазона 0-255 для хранения цветовых
компонент
Происходит отображение действительных значений
диапазона от 0 до 1 в 256 возможных целых чисел
Это приводит к тому, что многие RGB цвета не имеют
целочисленного представления в пространстве HSV
27. Цветовая модель HSL (HSI)
Данная цветовая модель задает цветовоепространство с терминах следующих компонент:
Hue – цветность
Saturation – насыщенность
Lightness (Luminosity, Luminance, Intensity) -
освещенность
28.
LHS
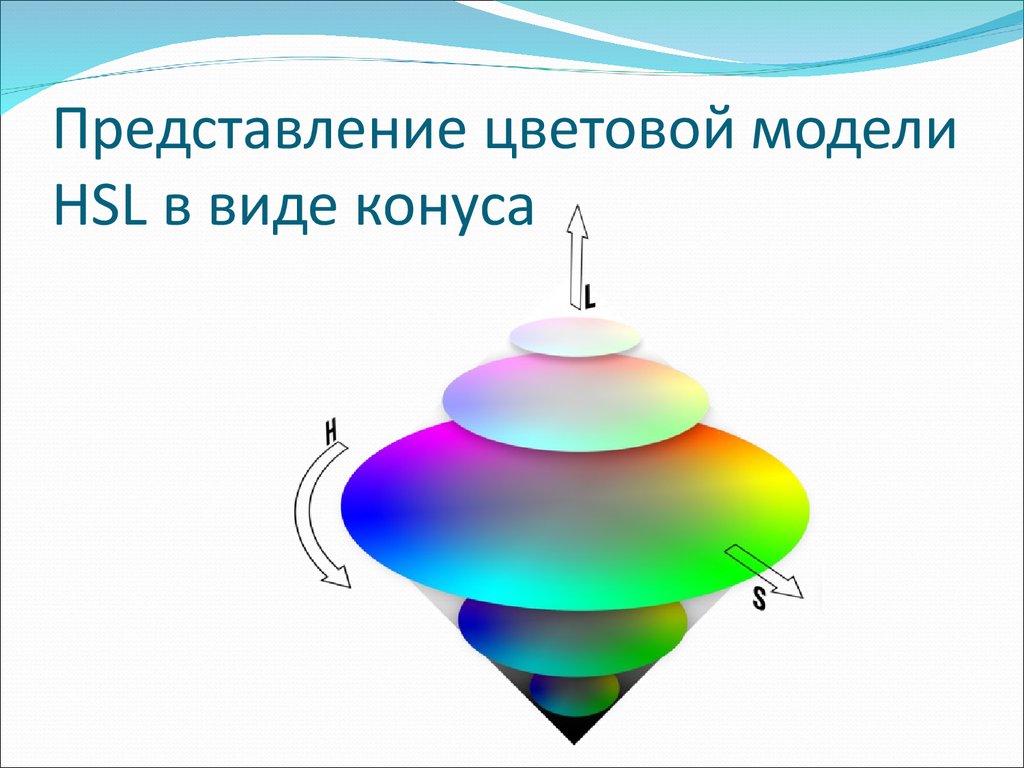
29. Представление цветовой модели HSL в виде конуса
30. Преобразование из RGB в HSL
R, G, B находятся в диапазоне 0 - 1MAX = max(R, G, B)
MIN = min(R, G, B)
31. Преобразование HSL в RGB
H: [0, 360); S, L: [0, 1];R, G, B: [0, 1]
Если S=0; то R=G=B=L
Для каждого c = R, G, B:
32. Сравнение моделей HSL и HSV
Модель HSL более интуитивно отражаетпонятие насыщенности и освещенности
Насыщенность в модели HSL всегда изменяется от
полностью насыщенного цвета к эквивалентному
серому цвету, в то время как в модели HSV при V=1
полностью насыщенный цвет переходит к белому
Освещенность в модели HSL изменяется от черного
через выбранное значение цветности – к белому, а в
модели HSV – проходит лишь половину пути – от
черного к выбранному цветному.
33. Другие цветовые модели
При передаче телевизионных аналоговыхсигналов используются следующие цветовые
модели:
YUV (используется в телевизионном сигнале PAL)
YDbDr (используется при передаче SECAM-сигнала)
YIQ (NTSC-сигнал)
В этих моделях Y-составляющая несет
яркостную составляющую изображения, а
остальные – информацию о цвете
Этот подход позволил перейти на передачу цветного
телевизионного сигнала, сохранив совместимость с
черно-белым телевидением
34. Итоги
Цветовые модели описывают способы передачицветовой информации в числовом виде
Идеальных цветовых моделей не существует. В
различных ситуациях наиболее удобной может
оказаться та или иная модель
35.
Психофизические аспектыцвета
36. Нелинейное восприятие цвета и света
У живых существ восприятие цвета (а также вкуса,запаха, веса) носит нелинейный характер
Например, с повышением яркости света
чувствительность глаза (способность различать
изменение в интенсивности) уменьшается
37. Закон Вебера-Фехнера (Weber-Fechner’s law)
Закон Вебера-Фехнера (WeberFechner’s law)Интенсивность ощущения пропорционально логарифму
интенсивности стимула
Новый раздражитель, чтобы отличаться по ощущениям от
предыдущего, должен отличаться от исходного на величину,
пропорциональную исходному раздражителю
Например, яркость люстры из 8-и ламп кажется ярче люстры
из 4-х ламп насколько, насколько люстра с 4 лампами ярче
люстры, в которой 2 лампы
где S0 — граничное значение интенсивности
раздражителя: если S < S0, раздражитель
38. Закон Стивенса (Stevens’ law)
Модификация закона Фехнера, согласнокоторой чувствительность носит не
логарифмический, а экспоненциальный
характер
Ψ(I)=kIa
Ψ –
психофизическая функция, определяющая
чувствительность к раздражителям
I – величина физического раздражителя
a – зависит от типа раздражителя
Для громкости равен 0,3
Для электрического удара 3,5
k – коэффициент пропорциональности
39. Нелинейность изменения яркости монитора
Яркость изображения на мониторе такжеизменяется нелинейным образом в
зависимости от величины исходного сигнала
Данный закон зависимости выходного сигнала от
входного определяется степенным законом:
Vout = Vin ,
Vin, Vout: [0, 1]
<0 – гамма-сжатие
>0 – гамма-расширение
40.
При переносе графического файла междукомпьютерами копия изображения может
выглядеть светлее или темнее, чем оригинал.
Ситуация усложняется, когда используются
различные ОС или аппаратные платформы
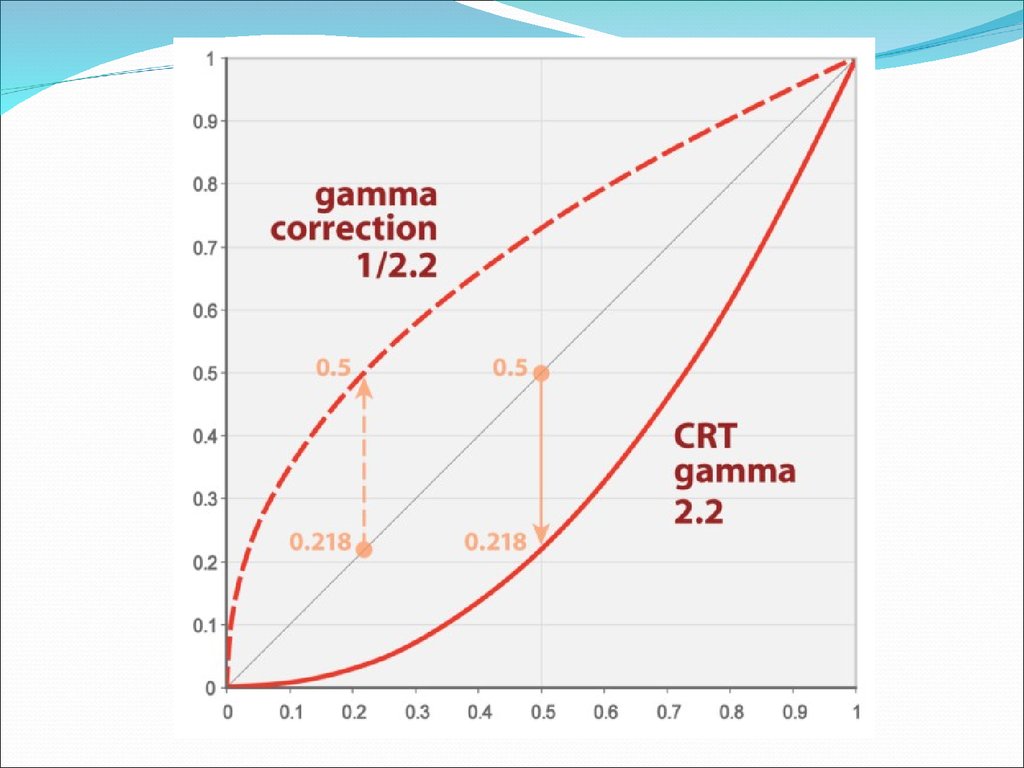
41. Гамма-коррекция
Система коррекции яркости изображения поотношению к хранимым или передаваемым
данным.
В графических файлах формата PNG хранится
информация о настройках монитора,
использованных при создании изображения
Vcorrected = Vsource(1/ )
42.
43.
Цифровая обработкасигналов
44. Сигналы
Сигнал - это информационная функция,несущая сообщение о физических свойствах,
состоянии или поведении какой-либо
физической системы, объекта или среды
Цели обработки сигналов:
извлечение определенных информационных
сведений, которые отображены в этих сигналах
преобразование этих сведений в форму, удобную
для восприятия и дальнейшего использования.
45. Размерность сигнала
Одномерный сигнал – это сигнал, значениякоторого зависят от одной независимой
переменной
Звуковой сигнал – зависимость амплитуды
колебаний воздуха в данной точке от времени
В общем случае сигналы являются многомерными
функциями пространственных, временных и
прочих независимых переменных
46. Изображение – тоже сигнал
Изображение – двухмерный сигнал – функцияцвета от координат
Это значит, что методы обработки сигналов
применимы к изображениям так же, как и другим
видам сигналов
47. Математическое описание сигналов
Математическое описание позволяетабстрагироваться от физической природы
сигнала и материальной формы его носителя:
классификации сигналов, сравнение,
моделирование систем обработки сигналов
Мат. описание сигнала - функциональной
зависимость определенного информационного
параметра сигнала от независимой переменной:
s(x), y(t) и т.п.
48. Аналоговые сигналы
Являются непрерывной функциейнепрерывного аргумента, (определены для
любого значения аргументов)
Источники аналоговых сигналов - физические
процессы, непрерывные в динамике своего развития
во времени или по другой независимой величине
Аналоговые сигналы при этом подобны
(«аналогичны») порождающим их процессам
49. График аналогового сигнала
50. Примеры аналоговых сигналов
Изменение электрического, магнитного,электромагнитного полей во времени и
пространстве
Звуковые волны (колебания воздуха)
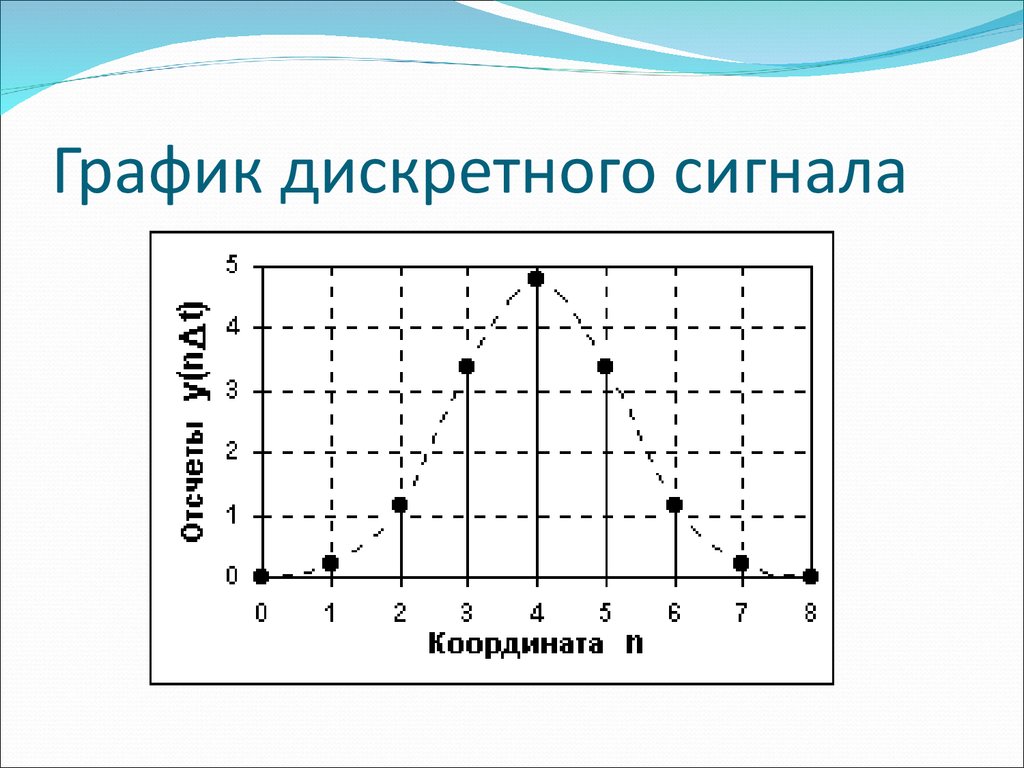
51. Дискретные сигналы
Дискретный сигнал по своим значениям – тоженепрерывная функция, но определенная по
дискретным значениям аргумента
Множество значений является счетным и
описывается дискретной последовательностью
отсчетов (samples) y(n*Δt)
Δt – интервал дискретизации (sampling time)
n = 0, 1, 2, …N
Величина f=1/ Δt – частота дискретизации (sampling
frequency, sampling rate)
52. График дискретного сигнала
53. Пример дискретизации изображения
ДискретизированиеДискретизированное
Оригинал
Изображение (32*32)
изображение
(128*128)
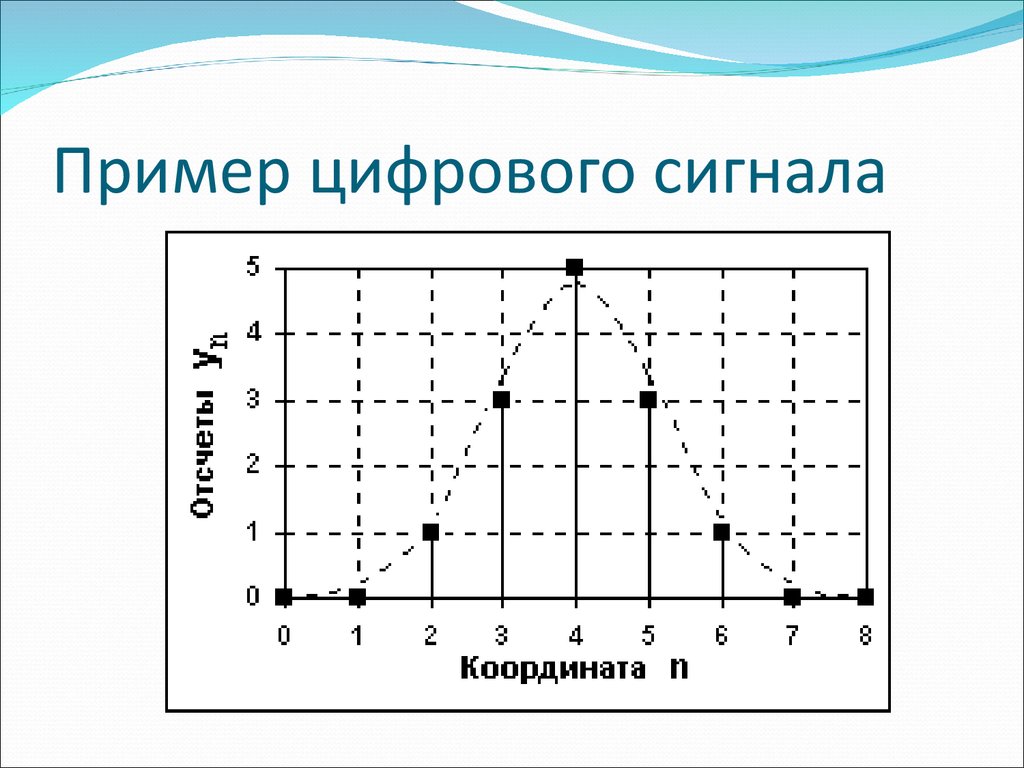
54. Цифровые сигналы
Цифровой сигнал квантован по своим значениями дискретен по аргументу
Он описывается решетчатой функцией
yn = Qk[y(n* Δt)]
Qk - функция квантования с числом уровней
квантования k
Интервалы квантования могут иметь как
равномерное, так и неравномерное распределение
(напр. логарифмическое)
55. Квантование (quantization)
Квантование по уровню - процесспреобразования бесконечных по принимаемым
значениям аналоговых отсчетов в конечное число
цифровых значений
Возникающие при этом ошибки округления
отсчетов называются ошибками квантования.
56. Пример цифрового сигнала
57. Пример квантования изображения
64цвета
Оригинал
цветов
416цвета
256
цветов
58. Источники цифровых сигналов
Аналоговые сигналы, подвергнутые оцифровкеЦифровой звук
Растровые изображения
Некоторые сигналы изначально относятся к классу
цифровых
Отсчеты количества гамма-квантов,
зарегистрированных по последовательным
интервалам времени
59. Представление сигналов в дискретных системах и ЭВМ
В дискретных системах и в ЭВМ сигнал всегдапредставлен с точностью до определенного
количества разрядов, а, следовательно, всегда
является цифровым
При описании сигналов функция квантования Q
обычно опускается (подразумевается равномерной
по умолчанию)
Обычно цифровые сигналы кодируются
последовательностью двоичных чисел определенной
разрядности
60.
Преобразования типовсигналов
61. Дискретизация аналогового сигнала
Операция дискретизации (discretization)преобразование аналоговых сигналов (функций),
непрерывных по аргументу, в функции мгновенных
значений сигналов по дискретному аргументу
Примеры
замер амплитуды звука в определенные моменты времени
62. Восстановление аналогового сигнала
Восстановление аналогового сигнала издискретного представления
Интерполяция дискретных данных
63. Теорема Котельникова
Если аналоговый сигнал x(t) имеет спектр,ограниченный частотой Fmax, то он может быть
однозначно и без потерь восстановлен по своим
дискретным отсчетам, взятым с частотой:
fdiscr≥2*Fmax
64. Следствия из теоремы Котельникова
Если максимальная частота в сигнале превышаетполовину частоты дискретизации, то способа
восстановить сигнал из дискретного в аналоговый без
искажений не существует
Из определения спектра сигнала следует, что
конечный по длительности сигнал имеет
бесконечно широкий спектр. Поэтому при
дискретизации конечного по длительности сигнала
(например песни на аудиодиск) невозможно
восстановление из отсчетов без потери качества
65. Аналого-цифровое преобразование
Операция квантования (АЦП – аналого-цифровое преобразование)
заключается в преобразовании дискретного сигнала
в цифровой, как правило, кодированный в двоичной
системе счисления
66. Цифро-аналоговое преобразование
Операция цифро-аналогового преобразованияЯвляется обратной операции квантования –
аналоговый сигнал восстанавливается из
дискретных значений путем сглаживания
67. Погрешности квантования
Квантование сигналов всегда выполняется сопределенной и неустранимой погрешностью (до
половины интервала квантования)
Поэтому операции АЦП и ЦАП не являются взаимно
обратными с абсолютной точностью
68. Преобразования типов сигналов на примере изображения
ОригиналВосстановление
Дискретизация +
аналогового
Квантованиесигнала
69. Спектральное представление сигнала
При анализе и обработке данных широкоиспользуется математическое описание сигналов
по аргументам, обратным аргументам
динамического представления
Обратный аргумент времени – частота
70.
Любой сколь угодно сложный по своей формесигнал, не имеющий разрывов первого рода
(бесконечных значений на интервале своего
задания), можно представить в виде суммы более
простых сигналов
Например – в виду суммы гармонических колебаний
(см. преобразование Фурье)
71. Цифровая обработка сигналов
Цифровая обработка сигналов оперирует сдискретными преобразованиями сигналов и
обрабатывающих данные сигналы систем
При помощи математических алгоритмов s(k)
преобразуется в некоторый другой сигнал s1(k)
имеющий требуемые свойства
72. Цифровые сигнальные процессоры
Цифровой сигнальный процессор (DSP) –специализированный микропроцессор,
предназначенный для цифровой обработки
сигналов в реальном времени
Область применения:
Кодирование и декодирование аудио/видео-потоков
Речевые и музыкальные синтезаторы
Распознавание речи и изображений
73. Дискретное преобразование Фурье (DFT – Discrete Fourier Transform)
Позволяет переводить дискретный сигнал извременного или пространственного представления
в частотное, выражая его в виде суммы
гармонических колебаний определенных частот
Обратное преобразование осуществляется при
помощи обратного преобразования Фурье
П
рямое
преобразование
Обратное
преобразование
74. Прямое дискретное преобразование Фурье
N - количество значений сигнала, измеренных за периодxn – измеренные значения сигнала в дискретных временных
точках
Xk – комплексные амплитуды синусоидальных сигналов,
слагающих исходные сигналы (обозначают одновременно
амплитуду и фазу)
|Xk|/N – амплитуда k-го синусоидального сигнала
arg(Xk) – фаза k-го синусоидального сигнала
k – частота k-ой синусоиды, измеренная в колебаниях за
период
75. Обратное дискретное преобразование Фурье
N - количество значений сигнала, измеренных за периодxn – измеренные значения сигнала в дискретных временных
точках
Xk – комплексные амплитуды синусоидальных сигналов,
слагающих исходные сигналы (обозначают одновременно
амплитуду и фазу)
|Xk|/N – амплитуда k-го синусоидального сигнала
arg(Xk) – фаза k-го синусоидального сигнала
k – частота k-ой синусоиды, измеренная в колебаниях за
период
76. Быстрое преобразование Фурье (FFT - Fast Fourier Transform)
Быстрое преобразование Фурье (FFT Fast Fourier Transform)Эффективная реализация дискретного
преобразования Фурье
Применяется для обработки дискретного сигнала,
состоящего из 2n отсчетов
77. Применение ДПФ и БПФ компьютерной графике
Частотный анализ и обработка изображений:Фильтрация частот
Шумоподавление
Повышение/понижение резкости
Компрессия изображений и видео
78. Свертка (convolution)
Свертка – это функция, показывающая "схожесть"одной функции и отражённой и сдвинутой копией
другой
Формула свертки
79. Свертка дискретных функций
Одномерный случай( f g )(m) f (n) g (m n)
n
Двумерный случай
( f g )( x, y ) f (k , p ) g ( x k , y p )
k, p
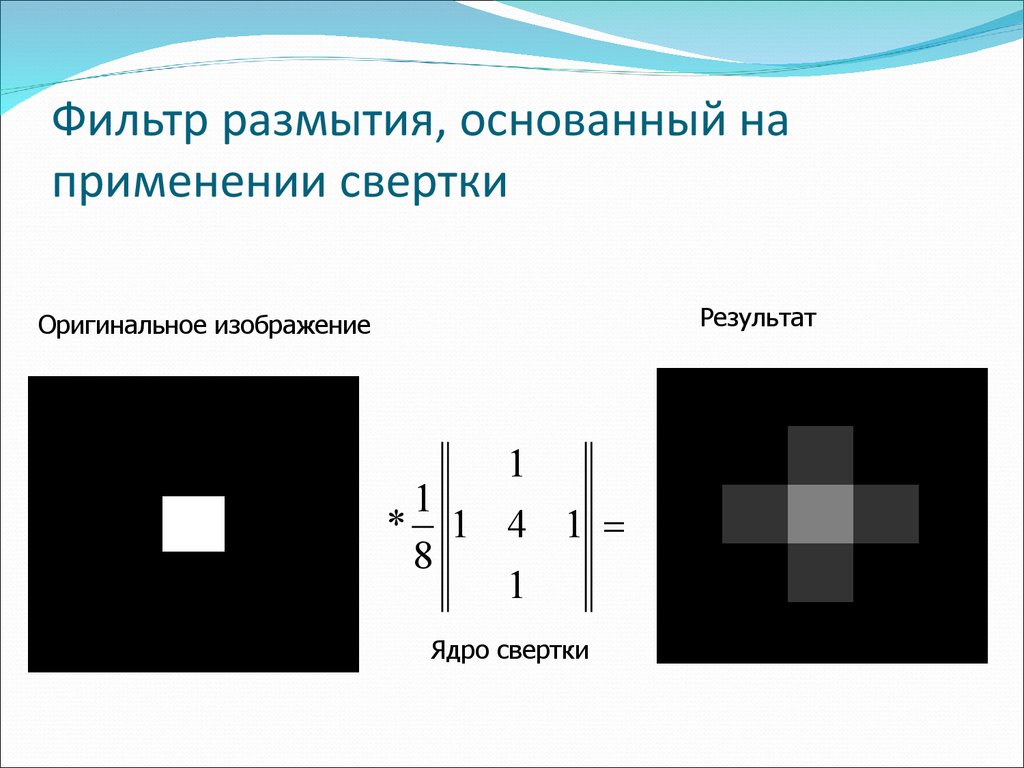
80. Фильтр размытия, основанный на применении свертки
РезультатОригинальное изображение
1
1
* 1 4 1
8
1
Ядро свертки
81. Применение свертки в компьютерной графике
ФильтрыРазмытие изображений (blur)
Повышение резкости (sharpen)
Выделение контуров (edge detection)
Размытие движения (Motion blur)
Тиснение (emboss)
82. Размытие Гаусса (Gaussian Blur)
1( u 2 v 2 ) /( 2 2 )
G (u , v)
e
2
2
83. Повышение резкости (sharpen)
1 21
1
2 22 2
10
1 2 1
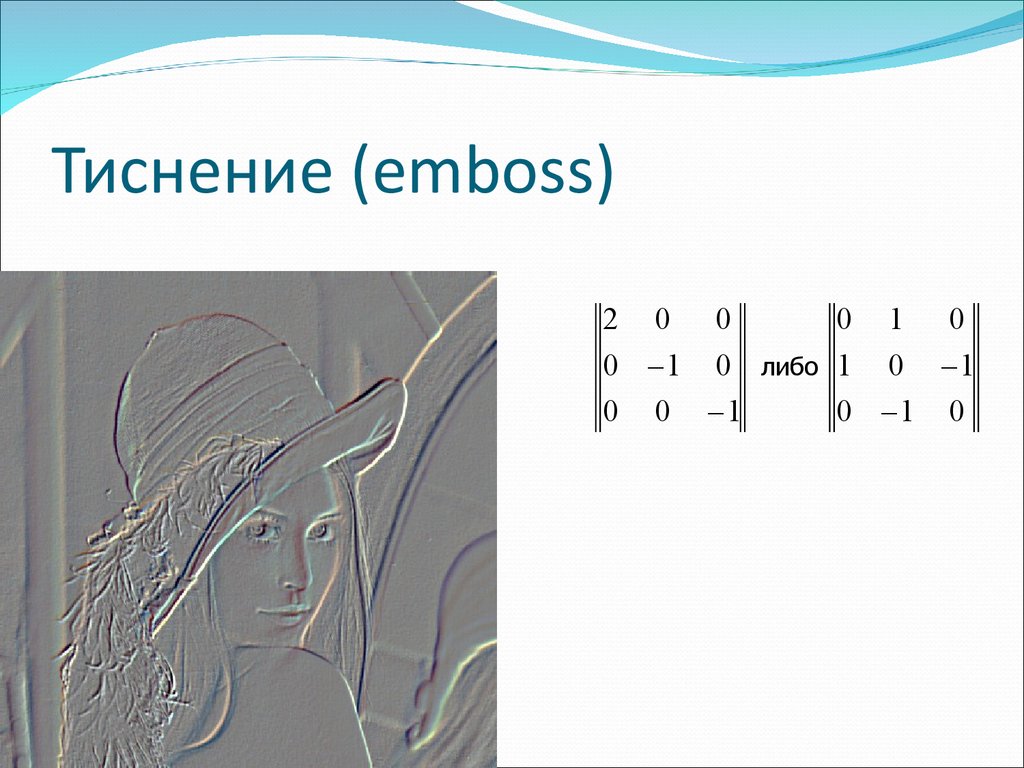
84. Тиснение (emboss)
2 00 1
0
0
0
1
0
0
либо 1
1
0
0 1
0
1
0
85. Выделение границ (Edge detection)
01
0
1
4
1
0
1
0
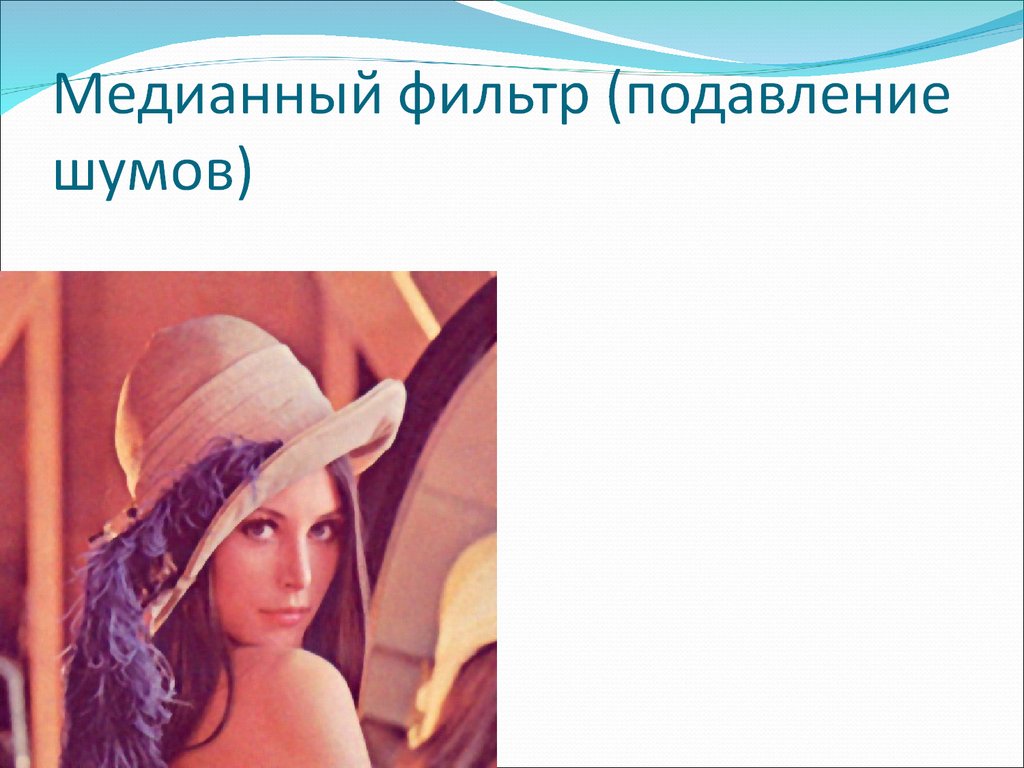
86. Медианный фильтр (подавление шумов)
87. Медианный фильтр
После применения фильтра пиксель принимаетзначение медианы значений пикселей в
окрестности
Для получения медианы необходимо отсортировать
значения пикселей (RGB-составляющие) в
окрестности по возрастанию и выбрать элемент из
середины массива
Количество элементов в выборке должно быть
нечетным
88. Смазывание движения (Motion Blur)
0 0 00 0
0 0 0 0 0
1
1 1 1 1 1
5
0 0 0 0 0
0 0 0 0 0
89. Выводы
Элементы теории сигналов нашли широкоеприменение в Компьютерной графике
Представление об изображениях как о двумерных
сигналах позволяет применять к ним
математические методы с целью улучшения
качества изображения, создания интересных
эффектов
90. Ссылки
RGBHSV
HSL
LAB
Свертка
Цифровая обработка сигналов
Медианный фильтр
















































































 Информатика
Информатика








