Похожие презентации:
Решение задач с помощью дифференциальных уравнений
1.
Практическое занятие № 12Решение задач с помощью
дифференциальных
уравнений
2.
Дифференциальным уравнением (ДУ)называется уравнение, содержащее производные
от искомой функции или её дифференциалы.
Решением ДУ является - функция
- Общие
Решения ДУ бывают: - Частные
Задача Коши - Найти частное решение
- с разделёнными переменными
Виды ДУ
- с разделяющимися переменными
3.
log 2 8 3log 3 81 4
log 5 5 1
lg 10 1
ln e 1
4.
5.
6.
Пример 1. Найдите частное решение дифференциальногоx
.
уравнения y y sin x 0 , если y=2, при
2
y y sin x 0
ln y cos x C
Решение:
ln y cos x ln e ln C
dy
y sin x 0 dx
dx
ln y ln C e cos x
dy y sin xdx 0
dy
sin xdx
y
dy
y sin xdx
y C e cos x общее решение
y=2 при x=
2
2 С у
cos
2
C e0 C C 2
y 2e cos x частное решение
7.
Пример 2. Скорость тела, выходящего из состояния покоя, равна5t 2 м/с по истечении t секунд.
Определите путь, пройденный телом за 3с.
Решение:
V 5t 2
dS
5t 2
dt
dS 5t 2 dt
2
dS
5
t
dt
5t 3
S
C общее решение
3
Т. к. тело выходит из состояния
покоя, то при t 0 S 0 0
5 03
0
С С 0
3
5t 3
S
частное решение
3
5 33
S 3
45 м
3
8.
Пример 3. Найдите уравнение линии, проходящейчерез точку М(1;3) и имеющей касательную, угловой
коэффициент которой равен 2х-3.
Решение:
Для нахождения частного решения
y 2 x 3
воспользуемся тем, что линия
dy
проходит через точку М(1;3),
2x 3
dx
т. е. х=1 и y=3.
dy 2 x 3 dx
dy 2x 3 dx
y x 2 3x C
общее решение
(семейство парабол)
3 1 3 С С 5
y x 2 3x 5 парабола.
9.
Пример 4. Скорость размножения некоторых бактерийпропорциональна их количеству в рассматриваемый
момент времени t. Количество бактерий утроилось в
течение 5ч. Найдите зависимость количества бактерий
от времени.
Пример 5. Скорость распада радия
пропорциональна его количеству в данный момент
времени. Найдите закон радиоактивного распада,
если известно, что через 1600 лет останется
половина первоначального количества радия.
10.
Пример 4. Скорость размножения некоторых бактерийпропорциональна их количеству в рассматриваемый
момент времени t. Количество бактерий утроилось в
течение 5ч. Найдите зависимость количества бактерий
от времени.
k 0
x
C
e
Cмомент
x 0 времени
0 в начальный
Пусть x 0 x 0 количество бактерий
x x t количество бактерий в момент
t.
x x 0времени
e kt
V
dx
за 5чколичеству
x увеличивае
тся в
kx скорость пропорциональна
бактерий
dt
dx
kx
dt
dx
x kdt
ln x kt C
3x 0 x 0 e 5 k
e5k 3
5k log e 3 ln 3
ln x ln e kt C
1
k ln 3 0.2 ln 3
5
x x 0 e 0.2 ln 3 t
x C e kt общее решение.
x x 0 e 0.22 t .
ln x kt ln e ln C
3раза
11.
Пример 5. Скорость распада радияпропорциональна его количеству в данный момент
времени. Найдите закон радиоактивного распада,
если известно, что через 1600 лет останется
половина первоначального количества радия.
R 0 начальное количество радия
0
t
0
R
R
R
Ce
C R0 я )
R R t количество радия
через0 t лет ( уменьшаетс
0
V
dR
1
1
1
1600k
1600k
kRt 1600 R R0
R 0 R0 e
e
dt
2
2
2
dR
1
kdt
1600
k
ln
ln 1 ln 2 ln 2
R
2
dR
R kdt k ln 2 0,6880 0,00043
1600
1600
ln R kt C
R R0 e 0, 00043t частное решение
ln R ln C e kt
R Ce kt общее решение
12.
Самостоятельно выполните задания Пр 12,которые находятся в группе
«291 СВ математика» в VK:
https://vk.com/club202706316
или
«293 СВ математика» в VK:
https://vk.com/club202706340


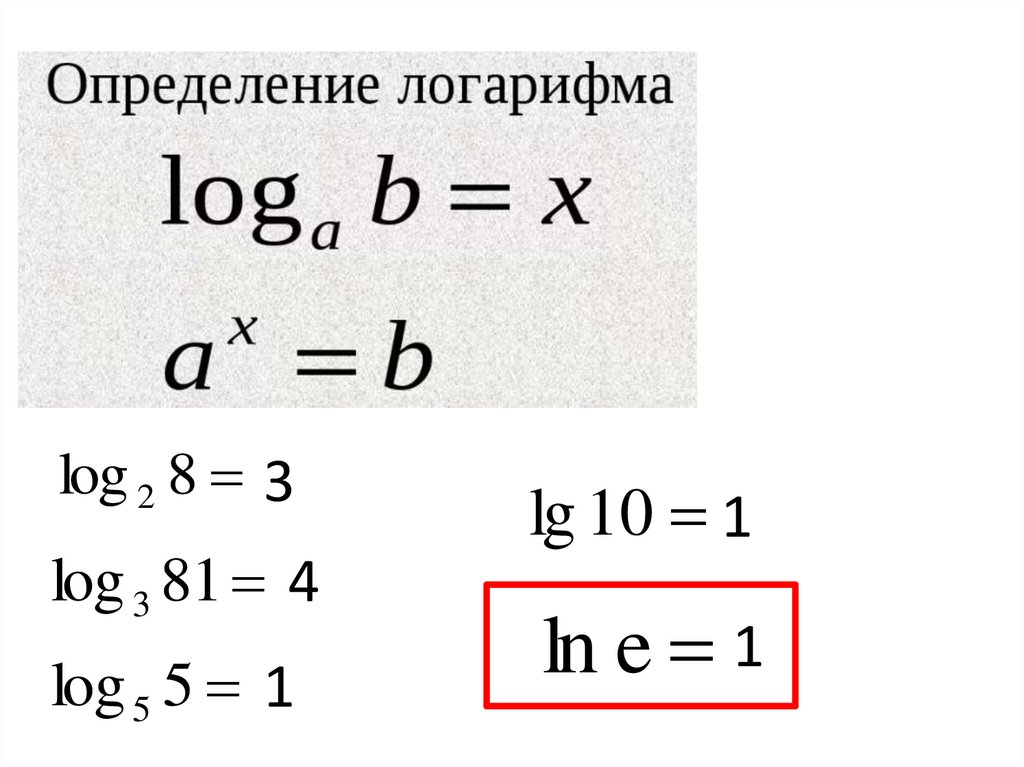








 Математика
Математика








