Дифференциальные уравнения

1. Дифференциальные уравнения

Определение дифференциального уравнения (ДУ).
Общее и частное решение ДУ. Задача Коши.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
ДУ с разделяющимися переменными. Алгоритм решения.
Однородные ДУ. Алгоритм решения.
Линейные ДУ. Алгоритм решения методом Бернулли
ДУ Бернулли. Алгоритм решения.
ДУ в полных дифференциалах. Алгоритм решения.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ
ПОРЯДКОВ
ДУ допускающие понижение порядка
Линейные (не)однородные ДУ. Теорема о структуре
общего решения.
Метод вариации постоянной. Метод неопределенных
коэффициентов.

2. Дифференциальные уравнения

Уравнение, связывающее независимую переменную
x с неизвестной функцией y(x) и ее производными до
некоторого порядка n включительно, называется
дифференциальным уравнением n-ого порядка.
дифференциальное уравнение
1-ого порядка
y 2 y x
2-ого порядка
2
y xy
3-его порядка
y 2 y 0

3. Дифференциальные уравнения

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
В ЧАСТНЫХ
ОБЫКНОВЕННОЕ
ПРОИЗВОДНЫХ
искомая функция зависит искомая функция зависит
от одной переменной
от нескольких переменных
Будем рассматривать обыкновенные
дифференциальные уравнения

4. Дифференциальные уравнения

ОБЩИЙ ВИД ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ n-ОГО ПОРЯДКА
F ( x, y, y ,..., y
(n)
) 0
(1)
F – некоторая функция от n+2 переменных, n 1
x – независимая переменная, y(x) – искомая функция,
y ( x),..., y ( n ) ( x) - ее производные
Дифференциальное уравнение n-ого порядка
называется разрешенным относительно старшей
производной, если оно имеет вид:
y
( n)
f ( x, y, y ,..., y
( n 1)
)

5. Дифференциальные уравнения

Решением дифференциального уравнения (1)
называется функция y(x), имеющая производные до
n-ого порядка включительно, и такая, что ее
подстановка в уравнение (1) обращает его в тождество
Решением уравнения
y 2 y
y ( x) e
2x
2x
y (e ) 2e
является функция
2x
y e
2x
2e
2x
2e
2x

6. Пример

y x
dy
dy
x
y
x dy xdx y
c1
dx
dx
2
2
2
dy
dy x
x
y
c1 dy
dx c1dx
dx 3 dx 2
2
x
y
c1 x c2 - общее решение
6
c1 const , c2 const
3
x
c1 2, c2 3 y 2 x 3 - частное решение
6
2

7. Дифференциальные уравнения

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИМЕЕТ
БЕСКОНЕЧНОЕ МНОЖЕСТВО РЕШЕНИЙ
Общее решение дифференциального уравнения
зависит от произвольных постоянных, число которых
равно порядку дифференциального уравнения
Частное решение дифференциального уравнения
получается из общего путем придания конкретных
значений произвольным постоянным

8. Дифференциальные уравнения

Задача о нахождении решения некоторого
дифференциального уравнения называется задачей
интегрирования данного дифференциального
уравнения
График решения дифференциального уравнения
называется интегральной кривой
Общим решением дифференциального уравнения (1)
n-ого порядка называется такое его решение
y ( x, с1 , с2 ,..., сn )
которое является функцией переменной x и n
произвольных независимых постоянных с1 , с2 ,..., сn

9. Пример

Из статистических данных известно, что для
некоторого региона число новорожденных и число
умерших за единицу времени пропорциональны
численности населения с коэффициентами
пропорциональности k 1 и k 2 соответственно.
Найти закон изменения численности населения с
течением времени (то есть описать протекание
демографического процесса)

10. Решение

Пусть y=y(t) – число жителей региона в момент
времени t.
Число родившихся в момент времени t равно k1y,
а число умерших равно k2y
Тогда прирост населения y за время t равен
разности между числом родившихся и умерших
за это время: y k1 y t k2 y t (k1 k2 ) y t
y
Обозначим k k1 k2 y ky t или
ky
t

11. Решение

Переходя к пределу при
уравнение y ky
t 0, получим
Решим это уравнение:
dy
dy
dy
ky kdt kdt ln y kt c1
dt
y
y
ln y kt ln с e
ln y
e
kt ln с
y ce
kt
C – постоянная, определяемая начальным
условием (численностью населения в начальный
kt
момент времени) y (0) M y (t ) Me

12. Дифференциальные уравнения

Отыскание частного решения дифференциального
уравнения (1) n-ого порядка, удовлетворяющего n
начальным условиям вида: y ( x0 ) y0
y ( x0 ) y
1
0
.................
называется задачей Коши
y
( n 1)
( x0 ) y 0
( n 1)
По n начальным условиям определяются значения
всех n произвольных постоянных, входящих в
общее решение диффер. уравнения n –ого порядка

13. Дифференциальные уравнения 1 порядка

ОБЩИЙ ВИД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 1-ОГО
ПОРЯДКА
F ( x, y, y ) 0
(2)
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ 1-ОГО ПОРЯДКА,
РАЗРЕШЕННОЕ ОТНОСИТЕЛЬНО СТАРШЕЙ
ПРОИЗВОДНОЙ
y f ( x, y )
(3)
f – некоторая функция двух переменных

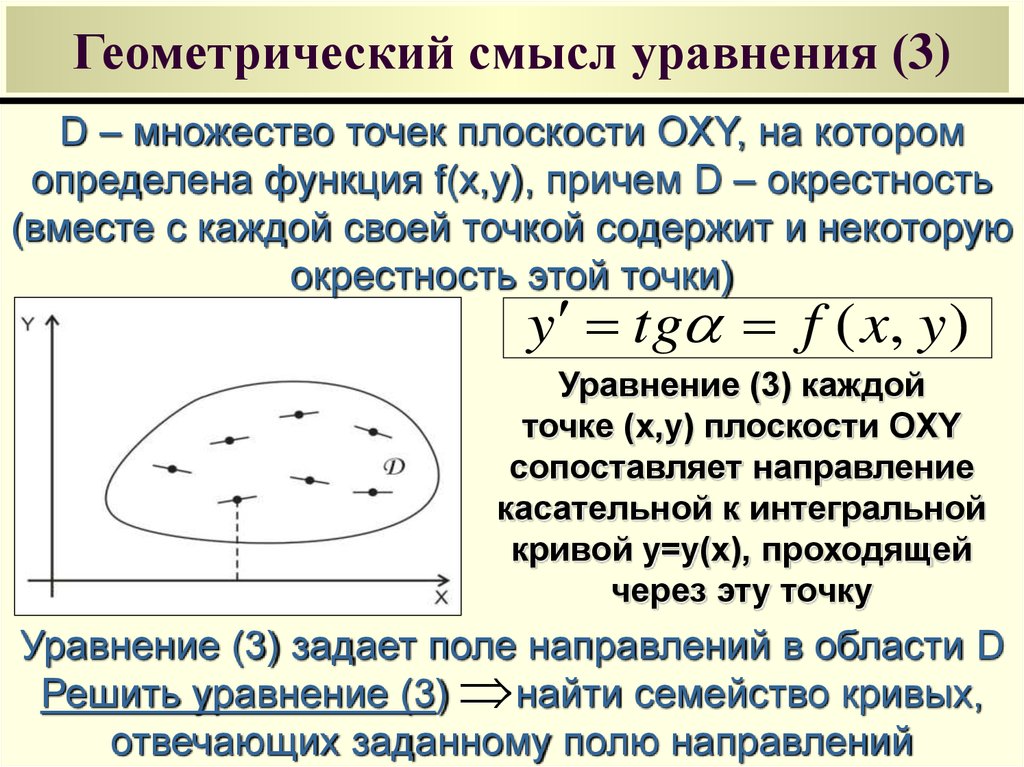
14. Геометрический смысл уравнения (3)

D – множество точек плоскости OXY, на котором
определена функция f(x,y), причем D – окрестность
(вместе с каждой своей точкой содержит и некоторую
окрестность этой точки)
y tg f ( x, y )
Уравнение (3) каждой
точке (x,y) плоскости OXY
сопоставляет направление
касательной к интегральной
кривой y=y(x), проходящей
через эту точку
Уравнение (3) задает поле направлений в области D
Решить уравнение (3) найти семейство кривых,
отвечающих заданному полю направлений

15. Пример

y
y
x
D – множество точек (x,y), где
x 0
Поле направлений можно построить на всей
плоскости, кроме оси ОY.
В каждой точке (x,y) угловой
коэффициент касательной
совпадает с угловым
коэффициентом прямой,
проходящей через данную
точку и начало координат
Вдоль этих прямых угловой коэффициент постоянен
y
с интегральными кривыми этого уравнения
x
являются прямые y=cx, где с – произв. постоянная

16. Дифференциальные уравнения

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИМЕЕТ
БЕСКОНЕЧНОЕ МНОЖЕСТВО РЕШЕНИЙ y ( x, c )
ДЛЯ ВЫДЕЛЕНИЯ КОНКРЕТНОГО РЕШЕНИЯ, МОЖНО
ЗАДАТЬ НАЧАЛЬНОЕ УСЛОВИЕ y ( x0 ) y0 (4)
Задача о нахождении решений дифференциального
уравнения (3), удовлетворяющих начальному
условию (4), называется задачей Коши

17. Дифференциальные уравнения

(о существовании и единственности решения
задачи Коши)
Если в уравнении y f ( x, y ) функция f(x,y) и ее частная
производная f y ( x, y ) непрерывны в некоторой
области D, содержащей точку ( x0 , y0 ) , то существует
единственное решение y (x) этого уравнения,
удовлетворяющее начальному условию y( x0 ) y0
При выполнении условий теоремы существует
единственная интегральная кривая
дифференциального уравнения, проходящая через
точку ( x0 , y0 )

18. Дифференциальные уравнения с разделяющимися переменными

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С РАЗДЕЛЕННЫМИ
ПЕРЕМЕННЫМИ
P( x)dx Q( y )dy 0
P( x)dx Q( y)dy 0
(5)
- ОБЩИЙ ИНТЕГРАЛ
уравнение с разделенными переменными
e dx ( y 1)dy 0
x
общий интеграл
2
y
e dx ( y 1)dy 0 e 2 y c
x
x

19. Дифференциальные уравнения с разделяющимися переменными

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С
РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
P1 ( x) Q1 ( y)dx P2 ( x) Q2 ( y)dy 0
(6)
Уравнение (6) сводится к уравнению (5) путем
почленного деления на Q1 ( y) P2 ( x) 0
P1 ( x)
Q2 ( y )
dx
dy 0
P2 ( x)
Q1 ( y )
P1 ( x)
Q2 ( y )
- ОБЩИЙ ИНТЕГРАЛ
dx
dy
0
P2 ( x)
Q1 ( y)

20. Дифференциальные уравнения с разделяющимися переменными

При проведении почленного деления
дифференциального уравнения на Q1 ( y) P2 ( x)
могут быть потеряны некоторые решения. Поэтому
следует отдельно решить уравнение Q1 ( y) P2 ( x) 0
и установить те решения дифференциального
уравнения, которые не могут быть получены из
общего решения – особые решения.

21. Дифференциальные уравнения с разделяющимися переменными

y p ( x) g ( y )
Данное уравнение сводится к уравнению с
разделенными переменными
dy
dy
y
p( x) g ( y )
dx
dx
dy
p( x)dx
g ( y)
dy
p
(
x
)
dx
g ( y)

22. Пример

y
y , y ( 4) 1
x
dy
y dy
dx
ln y c1 ln x ln c ln x
dx
x
y
x
c
y
x
- общее решение
c
4
y(4) 1 1 c 4 y
4
x
- частное решение

23. Пример

( ye 9 y) y e (1 y ) 0
x
x
2
1 y 0
y
e
dy x
dx, x
2
1 y
e 9
e 9 0
1
2
x
ln 1 y ln( e 9) c1
2
x
2
1
2
x
2
x
ln 1 y ln( e 9) ln c 1 y c(e 9)
2

24. Однородные дифференциальные уравнения 1-ого порядка

Функция f(x,y) называется однородной функцией
n-ого порядка, если f ( x, y ) n f ( x, y )
f ( x, y) x 2 xy -однородная функция 2 порядка
2 2
2
2
2
f ( x, y) x 2 x y ( x 2 xy) f ( x, y)
2
Дифференциальное уравнение y f ( x, y ) называется
однородным, если функция f(x,y) есть однородная
функция нулевого порядка, т.е. f ( x, y ) f ( x, y )

25. Однородные дифференциальные уравнения 1-ого порядка

Однородное дифференциальное уравнение можно
представить в виде:
y
y ( ) (8)
x
Если f(x,y) – однородная функция нулевого порядка,
то f ( x, y ) f ( x, y )
1
x y
y
Положим : f ( x, y ) f ( , ) f (1, )
x
x x
x
y
( )
x

26. Однородные дифференциальные уравнения 1-ого порядка

Однородное уравнение (8) преобразуется в
уравнение с разделяющимися переменными:
y
u y u x y u x u
x
Подставим в уравнение (8):
u x u (u )
u x (u ) u - уравнение с разделяющимися
переменными
Найдя его общее решение, следует заменить в нем u
на y . Получим общее решение исходного уравнения.
x

27. Однородные дифференциальные уравнения 1-ого порядка

Однородные уравнения часто задаются в
дифференциальной форме:
P( x, y )dx Q( x, y )dy 0
Это дифференциальное уравнение будет
однородным, если P(x,y) и Q(x,y) – однородные
функции одинакового порядка:
x y
1 n
P( , )
( ) P ( x, y )
dy
P ( x, y )
x
x
x
x y
1 n
dx
Q ( x, y )
Q( , )
( ) Q ( x, y )
x x
x

28. Пример

x y y
x
2
y
2
x y y
x y y
f ( x, y )
f ( x, y )
x
x
2 2
2 2
2
2
y
u y u x y u x u
x
(*)
x y y
x x u xu
2
1 u u
x
x
2
2
2
2 2
(**)

29. Пример

u x u 1 u u u x 1 u
du
dx x 0
,
2
2
x
1 u 0
1 u
2
2
arcsin u ln x c
u sin(ln x c)
y x sin(ln x
y 2
1 ( ) 0
x
c),
x y -особое решение

30. Линейные дифференциальные уравнения 1-ого порядка

Дифференциальное уравнение первого порядка
называется линейным, если его можно записать
y p( x) y g ( x) (9)
в виде
где p(x) и g(x) – заданные функции.
Искомая функция y и ее производная
y входят в уравнение, не перемножаясь между собой
МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦ. УРАВНЕНИЯ (9)
МЕТОД БЕРНУЛЛИ
МЕТОД ЛАГРАНЖА

31. Метод Бернулли

y
Решение уравнения (9) ищется в виде
u v , где u u ( x), v v( x)- неизвестные
функции от x, причем одна из них произвольна (но 0)
y u v u v
Подставим в (9): u v u v p ( x )uv q ( x )
u v u (v p( x)v) q( x) (10)
Подберем функцию v(x) так, чтобы v p ( x )v 0
dv
p ( x)v ln v p ( x)dx c
dx

32. Метод Бернулли

Так как функция v(x) подбирается свободно, то можно
принять c=0
v e
Подставим в (10): u v
p ( x ) dx
q (x) или
u e
p ( x ) dx
q ( x)
p ( x ) dx
u q ( x) e
p ( x ) dx
p ( x ) dx
du
q( x) e
u q( x) e
dx c
dx
p ( x ) dx
p ( x ) dx
y ( q ( x) e
dx c) e

33. Пример

2y
2
y
5x
x
y u v y u v u v
2
2
2
2
u v u v uv 5 x u v u (v v) 5 x
x
x
2
dv
2
1
v v 0
dx ln v 2 ln x ln 2
x
v
x
x
1
1
2
4
5
v 2 u 2 5 x u 5 x u x c
x
x
1
c
5
3
y ( x c) 2 x 2
x
x

34. Дифференциальные уравнения Бернулли

Дифференциальное уравнение Бернулли - это
уравнение вида
n
y p ( x) y g ( x) y
(11)
где n R; n 0, n 1
n=0 уравнение (11) становится линейным
дифференциальным уравнением первого порядка
n=1 уравнение (11) имеет вид дифференциального
уравнения с разделяющимися переменными
y ( g ( x) p ( x)) y
В дальнейшем будем считать, что n 0, n 1

35. Метод Бернулли

y 0
n
1 n
y y p ( x) y g ( x)
1 n
Выполним замену. Обозначим через z y
Разделим уравнение (11) на
z (1 n) y
n
y y
n
n
1
y
z
1 n
Линейное дифференциальное уравнение 1-ого
порядка относительно z
1
z p ( x ) z g ( x ) (12)
1 n
Решая его методом Бернулли, получим общее
1
1
решение z=z(x,c)
1 n
1 n
y z
( z ( x, c))

36. Пример

6x
Уравнение Бернулли
e
y y 2
6x
2
y
y e y
y
2
3
6x
y y y e
1
3
2
2
z y z 3 y y y y z
3
1
6x
6x
z z e z 3 z 3e
3
z u v z u v u v
6x
u v u v 3uv 3e
6x
u v u(v 3v) 3e

37. Пример

1
1
x
3
v 3v 0 dv dx ln v x v e
3v
3
3x
v e
e u 3e u 3e
3x
u e c
3x
6x
3x
z e (e
3x
y
3
3x
c) e
6x
ce
z e (e c)
x
3x
1
3
3x

38. Дифференциальные уравнения в полных дифференциалах

Уравнение вида P( x, y )dx Q( x, y )dy 0 (13)
называется уравнением в полных дифференциал.,
если левая часть этого уравнения является
полным дифференциалом функции u=u(x,y), т.е.
du ( x, y ) P( x, y )dx Q( x, y )dy
Если (13) является уравнением в полных
дифференциалах, то его можно записать как
du ( x, y ) 0 u ( x, y ) с - общий интеграл
уравнения (13) (с=const)

39. Дифференциальные уравнения в полных дифференциалах

Для того, чтобы P( x, y )dx Q( x, y )dy являлось полным
дифференциалом функции u=u(x,y) необходимо и
достаточно выполнение следующего условия
P( x, y ) Q( x, y )
y
x
(14)
Пусть условие (14) выполнено. Тогда
u
(
x
,
y
)
du ( x, y ) P( x, y )dx Q( x, y )dy
P ( x, y )
x
(15)
u ( x, y)
u ( x, y)
du ( x, y)
dx
dy u ( x, y ) Q( x, y)
x
y
y

40. Дифференциальные уравнения в полных дифференциалах

Проинтегрируем первое уравнение в (15) по x
u ( x, y ) P( x, y )dx c( y )
Найдем c(y). Для этого вычислим частную
производную полученного уравнения по переменной y
u ( x, y )
( P( x, y )dx) c ( y ) Q( x, y )
y
y
c ( y ) Q( x, y ) ( P( x, y )dx) (16)
y

41. Дифференциальные уравнения в полных дифференциалах

Проинтегрируем (16). Получим
c( y ) (Q( x, y ) ( P( x, y )dx)) dy c
y
c const
u ( x, y) P( x, y)dx (Q( x, y) ( P( x, y)dx)) dy c
y
Приравнивая полученное выражение к константе c,
записывают общий интеграл уравнения (13)

42. Уравнения, допускающие понижение порядка

Метод понижения порядка состоит в том, что с
помощью замены переменной (подстановки) данное
дифференциальное уравнение сводится к уравнению,
порядок которого ниже.
y f (x)
(1)
y p( x) y p ( x)
p f (x) - дифференциальное
Введем функцию p(x):
Таким образом
уравнение 1-ого порядка, решив которое (найдя p(x)),
решим уравнение y p (x ) , т.е. решим (1)

43. Уравнения, допускающие понижение порядка

На практике порядок понижается путем
последовательного интегрирования уравнения
y f (x)
(1)
dy
y ( y )
из равенства (1) dy f ( x)dx
dx
Интегрируя,имеем y f ( x) dx или y 1 ( x) с1
Интегрируя y
( 1 ( x) с1 )dx y 2 ( x) с1 x c2
y
(n)
f ( x)
n 1
(1’)
n 2
x
x
y n ( x) с1
c2
... cn
(n 1)!
(n 2)!

44. Пример

y
( 4)
sin 2 x
1
y sin 2 xdx cos 2 x c1
2
1
1
y ( cos 2 x c1 )dx sin 2 x c1 x c2
2
4
2
1
x
y cos 2 x c1 c2 x c3
8
2
3
2
1
x
x
y sin 2 x c1 c2 c3 x c4
16
6
2

45. Уравнения, допускающие понижение порядка

( не содержит явно искомую функцию y)
y f ( x, y )
(2)
y p( x) y p ( x)
p f ( x, p) - дифференциальное
Введем функцию p(x):
Таким образом
уравнение 1-ого порядка, общим решением которого
является функция p ( x, с1 )
Заменяя
p y имеем y ( x, c1 )
y ( x, c1 )dx c2

46. Уравнения, допускающие понижение порядка

(k )
F ( x, y , y
( k 1)
,..., y ) 0
(n)
(3)
Порядок уравнения (3) можно понизить на k единиц
(k )
p ( x)
положив y
Тогда:
y
( k 1)
p ( x),..., y
( n)
p
( n k )
( x)
Уравнение (3) примет вид:
F ( x, p, p ,..., p
( n k )
) 0

47. Пример

y
y 0
x
y p , где p p(x) y p
p
p 0 - уравнение с разделяющимися
x
переменными
dp dx
p c1 x y c1 x
p
x
2
x
y c1 xdx c1
c2
2

48. Уравнения, допускающие понижение порядка

( не содержит явно независимую переменную x)
y f ( y, y )
(4)
y p , где p p( y ( x))
dy dp( y) dp( y) dy dp( y)
dp( y)
y
y
p
dx
dx
dy dx
dy
dy
dp
p
f
(
y
,
p
)
Таким образом
- дифференциальное
dy
уравнение 1-ого порядка, общим решением которого
является функция p ( y, с1 )
Введем функцию p=p(y):

49. Уравнения, допускающие понижение порядка

Заменяя p y имеем y ( y, c1 ) - уравнение
с разделяющимися переменными
dy
dy
( y, c1 )
dx
dx
( y, c1 )
Интегрируя, имеем:
dy
x
с
2
( y, c1 )

50. Уравнения, допускающие понижение порядка

F ( y, y , y ,..., y ) 0
( n)
(5)
Порядок уравнения (5) можно понизить на единицу
положив y p , где p p ( y )
По правилу дифференцирования сложной функции:
dp
y p
dy
d
d
dy
2
y ( p p y ) ( p p y ) p(( p y ) p p yy )
dx
dy
dx
и т.д.

51. Пример

Найти частное решение уравнения
y ( y ) y ( y 1) 0
2
удовлетворяющее начальным условиям
y (0) 2, y (0) 2
dp
dp
2
y p( y) y p p p p( y 1) 0
dy
dy
dp
p y 1 0
Так как p 0 , то
dy
dp
p 1 y (*) - линейное дифференциальное
dy
уравнение 1-ого порядка

52. Пример

Решим уравнение (*) методом Бернулли:
p u v p u v u v
u v uv uv 1 y
u v u (v v) 1 y
y
y
y
v v 0 v e
u e 1 y u ye c1
y
y
y
p uv ( ye c1 )e y c1e
y
y y c1e
x
Так как y (0) 2 , то c1 0 y y y c2e
Так как y (0) 2 , то c 2 y 2e x
2

53. Линейные дифференциальные уравнения n-ого порядка

Дифференциальное уравнение n-ого порядка
называется линейным, если его можно записать
(n)
( n 1)
... an ( x) y f ( x) (1)
в виде y a1 ( x) y
где a1 ( x), a2 ( x)...an ( x) – непрерывные функции.
( о существовании и единственности решения)
Пусть функции a1 ( x),..., an ( x), f ( x) – непрерывные
функции на отрезке [a,b], тогда существует,
причем единственное решение y(x) уравнения (1),
удовлетворяющее начальным условиям:
1
( n 1)
n 1
y ( x0 ) y0 , y ( x0 ) y0 ,..., y ( x0 ) y0 , x0 a, b (2)

54. Линейные дифференциальные уравнения n-ого порядка

Уравнение вида
y
(n)
a1 ( x) y
( n 1)
... an ( x) y f ( x)
(1)
называется линейным неоднородным
дифференциальным уравнением n-ого порядка
Уравнение вида
y
(n)
a1 ( x) y
( n 1)
... an ( x) y 0
(3)
называется линейным однородным
дифференциальным уравнением n-ого порядка,
соответствующее уравнению (1)

55. Линейные дифференциальные уравнения n-ого порядка

( о структуре решения линейного неоднородного
дифференциального уравнения )
Общее решение линейного неоднородного
дифференциального уравнения (1) есть сумма
частного решения yчн (x) этого уравнения и общего
решения yоо (x) соответствующего линейного
однородного уравнения (3).
ОБЩЕЕ РЕШЕНИЕ НЕОДНОРОДНОГО
УРАВНЕНИЯ
yон ( x) yчн ( x) yоо ( x)
(4)

56. Линейные однородные дифференциальные уравнения

Функции y1 ( x), y2 ( x),..., yn ( x) называются линейно
зависимыми на отрезке [a,b], если существуют
n
такие числа ci 0, i 1, n : ci 0 ,что выполняется
1
следующееi тождество:
с1 y1 ( x) с2 y2 ( x) ... сn yn ( x) 0, x a, b (5)
Если тождество (5) выполняется в случае, когда
все с1 , с2 ,..., сn равны нулю, то функции
y1 ( x), y2 ( x),..., yn ( x)
называются линейно независимыми

57. Линейные однородные дифференциальные уравнения

ОПРЕДЕЛИТЕЛЬ ВРОНСКОГО, ПОСТРОЕННЫЙ
ДЛЯ СИСТЕМЫ ФУНКЦИЙ
y1 ( x), y2 ( x),..., yn ( x)
y1 ( x)
y1 ( x)
W ( y1 , y2 ,..., yn ) W ( x)
y2 ( x) ...
y2 ( x) ...
...
...
( n 1)
1
( n 1)
2
y
( x) y
yn ( x)
yn ( x)
...
( x) ... y
...
( n 1)
n
( x)

58. Линейные однородные дифференциальные уравнения

Свойства определителя Вронского:
Если функции y1 ( x), y2 ( x),..., yn ( x) линейно
1.
зависимы, то их определитель Вронского
тождественно равен нулю на отрезке [a,b].
Если функции y1 ( x), y2 ( x),..., yn ( x) линейно
независимые решения линейного однородного
2. дифференциального уравнения, определенные
на отрезке [a,b], то их определитель Вронского
ни в одной точке отрезка [a,b] не равен нулю, т.е
W ( y1 , y2 ,..., yn ) 0, x a, b

59. Линейные однородные дифференциальные уравнения

Система функций y ( x),..., y ( x) , состоящая из n
1
n
линейно независимых решений линейного
однородного дифференциального уравнения (3)
называется фундаментальной системой решений
(ФСР) этого уравнения.
( о структуре общего решения линейного однородного
дифференциального уравнения)
Пусть y1 ( x),..., yn ( x) - ФСР линейного однородного
дифференциального уравнения (3). Тогда общее
решение этого уравнения задается формулой
yоо ( x) с1 y1 ( x) с2 y2 ( x) ... сn yn ( x) (6)

60. Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

y py qy 0
(7)
p, q – действительные числа
ОБЩЕЕ РЕШЕНИЕ УРАВНЕНИЯ (7)
yоо ( x) с1 y1 ( x) с2 y2 ( x)
y1 ( x), y2 ( x) - ФСР уравнения (7)
с1 , с2 - произвольные числа
(8)

61. Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

МЕТОД ЭЙЛЕРА
Решение уравнения (7) будем искать в виде:
y( x) e , - неизвестное число
x
x
2 x
y ( x) e , y ( x) e
Подставим решение в уравнение (7):
2 x
x
x
e p e qe 0
Характеристическое уравнение
p q 0
2
(9)

62. Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

p q 0
2
(9)
Случай 1:
D p 4q 0
2
1, 2
- два различных действительных
решения уравнения (9)
1 x
y1 ( x) e - решения уравнения (7)
2 x
y2 ( x ) e
1 x
2 x
(10)
yоо ( x) с1e с2 e

63. Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

1 x
y1 ( x) e , y2 ( x) e
2 x
- ФСР уравнения (7)
( т.к. по 2 свойству определителя Вронского
решения линейно независимы)
W ( y1 , y2 )
e
1 x
1e
1 x
e
2 x
2e
D 0 2 1 0
1 x
2 x
e 0, e 0
2 x
1 x 2 x
( 2 1 )e e
0

64. Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

p q 0
2
(9)
Случай 2:
D p 4q 0
p
1 2 - решения уравнения (9)
p 2
x
2
y1 ( x) e
y2 ( x) xe
2
p
x - решения уравнения (7)
2
p
p
x
x
(11)
2
2
оо
1
2
y ( x) с e
с xe

65. Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

y1 ( x) e
p
x
2
p
x
2 - ФСР уравнения (7)
, y2 ( x) xe
( т.к. по 2 свойству определителя Вронского
решения линейно независимы)
p
x
2
p
x
2
e
xe
px
p e
W ( y1 , y2 ) p p x
0
x
p
e 2 (1 x)e 2
2
2

66. Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

p
x
2
Покажем, что y2 ( x) xe
является
решением уравнения (7)
y2 ( x ) e
p
x
2
p
(1 x); y2 ( x) e
2
p
x
2
2
p
( p x)
4
Подставим в уравнение (7):
p
x
2
2
p
x
2
p
x
2
p
p
e ( p
x) pe (1 x) qxe 0
4
2
2
2
p
p
(
q) x 0 0 0, т.к. D 0 q 0
4
4

67. Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

p q 0
2
(9)
D p 4q 0
p
D - два различных комплексных
1, 2 i
решения уравнения (9)
2
4
2
Случай 3:
x
y1 ( x) e sin x
x
y2 ( x) e cos x
x
p
,
2
D
4
- решения уравнения (7)
x
yоо ( x) с1e sin x с2 e cos x
(12)

68. Пример

y 2 y 2 y 0
2 2 0
D 4 8 4 0
2
2 2i
1, 2
1 i
2
x
x
y1 e sin x, y2 e cos x
yоо ( x) с1e sin x с2 e cos x
x
x

69. Линейные неоднородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

y py qy f (x)
(1)
p, q – действительные числа
ОБЩЕЕ РЕШЕНИЕ УРАВНЕНИЯ (1)
yон ( x) yоо ( x) yчн ( x)
yчн (x) - частное решение уравнения (1)
yоо (x) -общее решение соответствующего
однородного уравнения (2)
y py qy 0
(2)

70. Линейные неоднородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

МЕТОД ВАРИАЦИИ ПОСТОЯННОЙ
Построение решения уравнения (2) рассмотрено ранее
Пусть
y1 ( x), y2 ( x) - ФСР уравнения (2)
yчн ( x) с1 ( x) y1 ( x) с2 ( x) y2 ( x)
с1 ( x), с2 ( x) - неизвестные функции
(3)

71. Линейные неоднородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

Подставим решение вида yчн с1 y1 с2 y2
в уравнение (1)
Для этого предварительно вычислим
производную этого решения
yчн (с1 y1 с2 y2 ) (с1 y1 с2 y2 )
Потребуем дополнительно с1 y1 с2 y2 0 (4)
yчн с1 y1 с2 y2
yчн с1 y1 с1 y1 с2 y2 с2 y2

72. Линейные неоднородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

yчн , yчн , yчн в уравнение (1)
( y1 py1 qy1 )с1 ( y2 py2 qy2 )с2
с1 y1 с2 y2 f ( x)
Подставим
Так как y1 ( x), y2 ( x)- решения уравнения (2),
то выражения в скобках равны нулю
с1 y1 с2 y2 f ( x)
(5)

73. Линейные неоднородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

Объединим условия (4) и (5) в одну систему
с1 y1 с2 y2 0
с1 y1 с2 y2 f ( x)
(6)
Решением системы (6) является:
y2 f ( x)
с1 ( x)
dx
W ( y1 , y2 )
y1 f ( x)
с2 ( x )
dx
W ( y1 , y2 )
Найденные выражения c1(x) и c2(x) подставим в (3)

74. Пример

y y 6e
yон ( x) yоо ( x) yчн ( x)
2x
НАЙДЕМ ОБЩЕЕ РЕШЕНИЕ СООТВЕТСТВУЮЩЕГО
ОДНОРОДНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
yоо ( x) ?
y y 0
2
1 0 1
x
x
e , e - ФСР
x
x
yоо ( x) c1e c2 e

75. Пример

НАЙДЕМ ЧАСТНОЕ РЕШЕНИЕ НЕОДНОРОДНОГО
ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ yчн ( x) ?
yчн ( x) c1 ( x)e
x
c2 ( x ) e
x
3x
x
x
c1 e c2 e 0 c1 e
x
x
x
2x
c2 3e
c
e
c
e
6
e
2
1
3x x
x x
2x
yчн ( x) e e 3e e 2e
yон ( x) c1e
x
c2 e 2e
x
x

76. Линейные неоднородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ
y py qy f (x)
(1)
p, q – действительные числа
x
f ( x) e ( Pn ( x) cos x Qm ( x) sin x)
, - заданные постоянные
Pn ( x), Qm ( x) - многочлены степени n и m
(7)
соответственно, зависящие от x

77. Линейные неоднородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

r x
yчн ( x) x e ( Al ( x) cos x Bl ( x) sin x) (8)
r - показатель кратности корня i
2
характеристического уравнения p q 0
Al ( x), Bl ( x) - многочлены степени l max m, n
зависящие от x с неопределенными
коэффициентами A0 , A1 ,..., Al , B0 , B1 ,..., Bl
l 1
l 2
Al ( x) A0 x A1 x A2 x ... Al
l
l 1
l 2
Bl ( x) B0 x B1 x B2 x ... Bl
l

78. Линейные неоднородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами

Замечания:
Если в выражение (7) в функцию f(x) входит
1. хотя бы одна из функций cos x или sin x,то
в частном решении yчн (x) надо вводить обе
функции
Если правая часть уравнения (1) равна сумме
нескольких различных функций рассматриваемой
структуры (7), то для отыскания частного
2.
решения такого уравнения надо использовать
теорему о наложении решений, т.е. надо найти
частные решения соответствующих отдельных
слагаемых правой части, а затем взять их сумму

79. Пример

4x
y 2 y 3 y e
yон ( x) yоо ( x) yчн ( x)
НАЙДЕМ ОБЩЕЕ РЕШЕНИЕ СООТВЕТСТВУЮЩЕГО
ОДНОРОДНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
yоо ( x) ?
y 2 y 3 y 0
2
2 3 0 1 1; 2 3
x
3 x - ФСР
e ,e
x
3x
yоо ( x) c1e c2 e

80. Пример

НАЙДЕМ ЧАСТНОЕ РЕШЕНИЕ НЕОДНОРОДНОГО
ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ yчн ( x) ?
yчн ( x) Ae
4x
4x
yчн ( x) 4 Ae ; yчн ( x) 16 Ae
4x
8 Ae 3 Ae e
1 4x
1
yчн ( x ) e
5A 1 A
5
5
16 Ae
4x
yон ( x ) c1e
4x
x
c2 e
4x
3x
4x
1 4x
e
5