Похожие презентации:
Представление зависимостей между величинами. О статистике и статистических данных. Метод наименьших квадратов
1. ПРЕДСТАВЛЕНИЕ ЗАВИСИМОСТЕЙ МЕЖДУ ВЕЛИЧИНАМИ. О СТАТИСТИКЕ И СТАТИСТИЧЕСКИХ ДАННЫХ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.
2. ПРИМЕРЫ ЗАВИСИМОСТЕЙ.
• Время падения тела на землю зависитот первоначальной высоты;
• Давление зависит от температуры газа
в баллоне;
• Частота заболевания жителей
бронхиальной астмой зависит от
качества городского воздуха.
3. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ЗАВИСИМОСТЕЙ
• Математическаямодель
• Табличный способ.
• Графический.
4. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ЗАВИСИМОСТЕЙ.
1. Математическая модель совокупность количественныххарактеристик некоторого объекта
(процесса) и связей между ними,
представленных языке математики.
t
2H
;
g
t 0C
P P0 (1
273
5. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ЗАВИСИМОСТЕЙ.
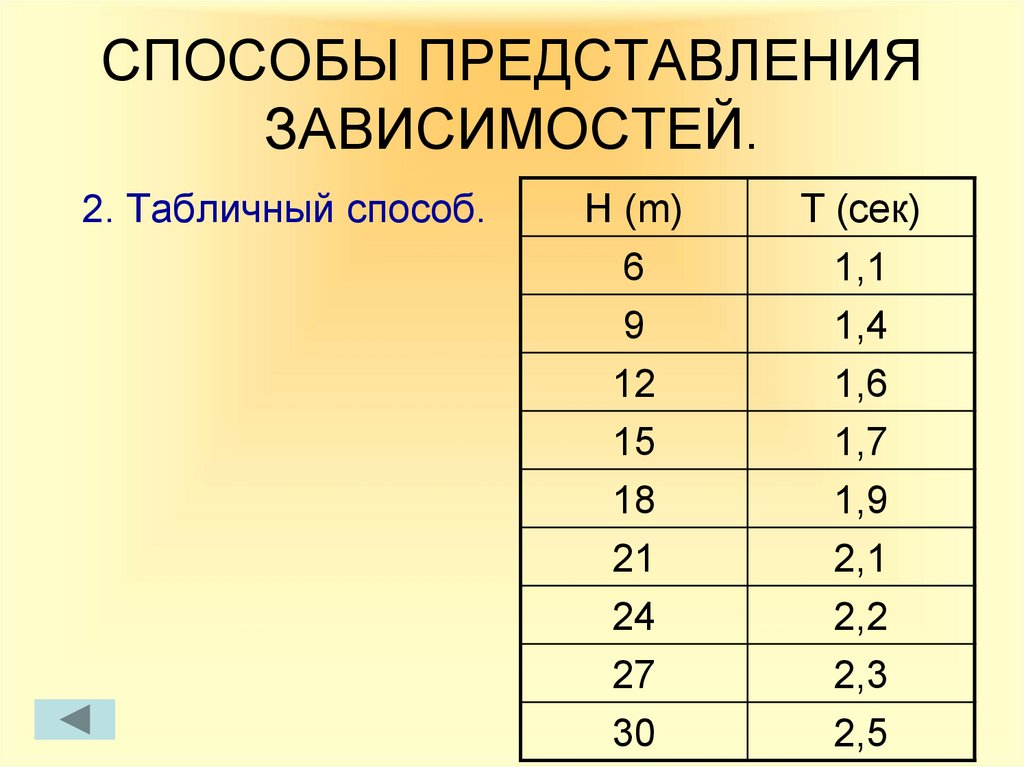
2. Табличный способ.H (m)
6
9
12
15
18
21
24
27
30
T (сек)
1,1
1,4
1,6
1,7
1,9
2,1
2,2
2,3
2,5
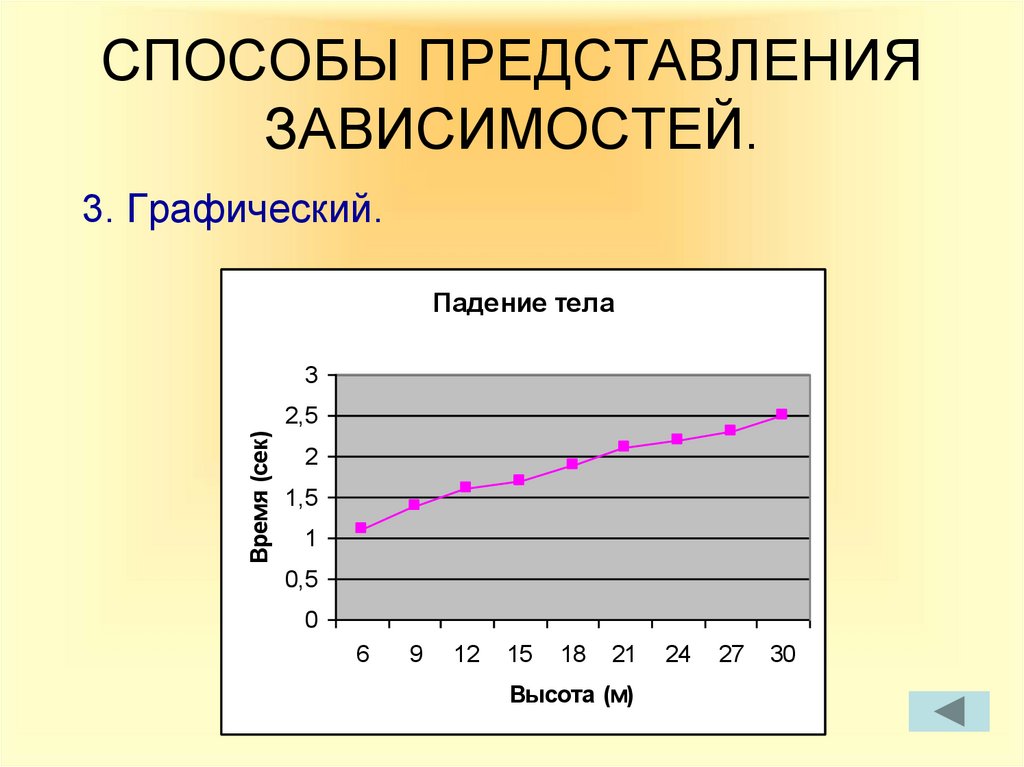
6. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ЗАВИСИМОСТЕЙ.
3. Графический.Падение тела
3
Время (сек)
2,5
2
1,5
1
0,5
0
6
9
12
15
18
21
Высота (м)
24
27
30
7. О СТАТИСТИКЕ И СТАТИСТИЧЕСКИХ ДАННЫХ.
Для решения задачи о бронхиальнойастме помогает статистика – наука о
сборе, измерении и анализе массовых
количественных данных.
Специалисты по медицинской
статистике проводят сбор данных о
средней концентрации угарного газа и о
заболеваемости астмой.
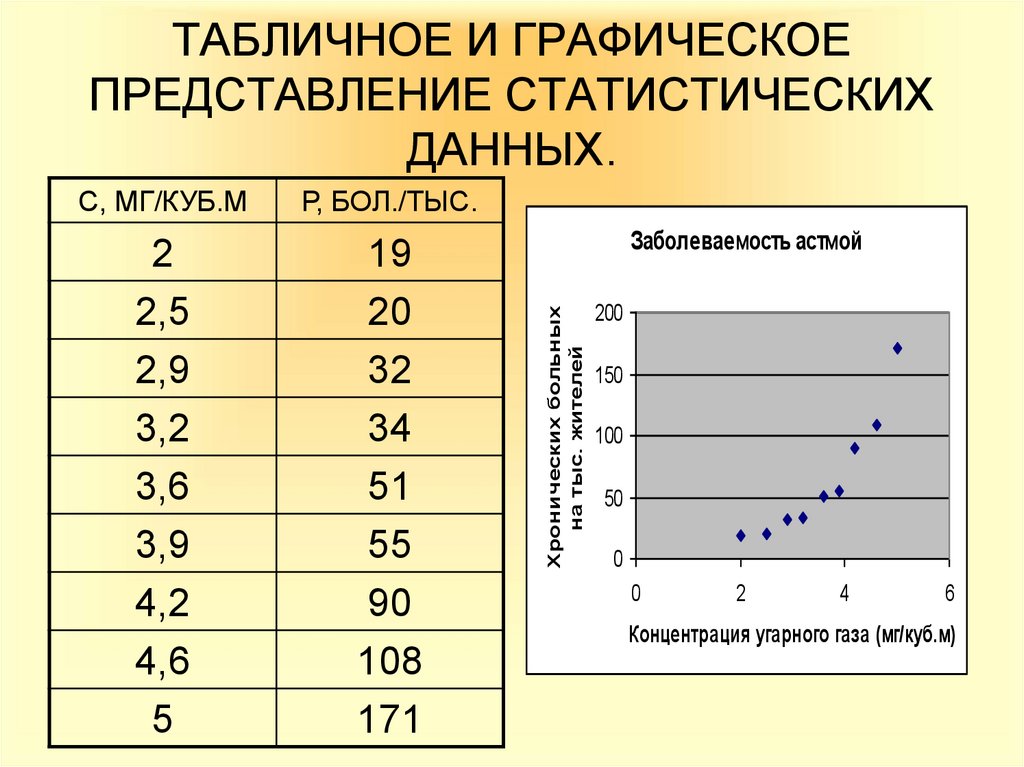
8. ТАБЛИЧНОЕ И ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ.
22,5
2,9
3,2
3,6
3,9
4,2
4,6
5
Р, БОЛ./ТЫС.
19
20
32
34
51
55
90
108
171
Заболеваемость астмой
Хронических больных
на тыс. жителей
С, МГ/КУБ.М
200
150
100
50
0
0
2
4
6
Концентрация угарного газа (мг/куб.м)
9.
Регрессионная модель – это функция,описывающая зависимость между
количественными характеристиками
сложных систем.
Получение регрессионной модели
происходит в 2 этапа:
1. подбор вида функции;
2. вычисление параметров функции.
10. ПОДБОР ВИДА ФУНКЦИИ
проводится среди следующих функцийy ax b линейная
y ax bx c квадратичная
2
y a ln( x) b логарифмич еская
y ae экспоненциальная
bx
y ax степенная
b
11.
y = 21,845x 2 - 106,97x +180
150,21
160
2
140
R = 0,9768
120
Ряд1
100
80
Линейный
60
(Ряд1)
40
20
0
0
2
4
200
150
y = 46,361x - 99,881
R2 = 0,8304
100
50
0
-50
0
2
4
6
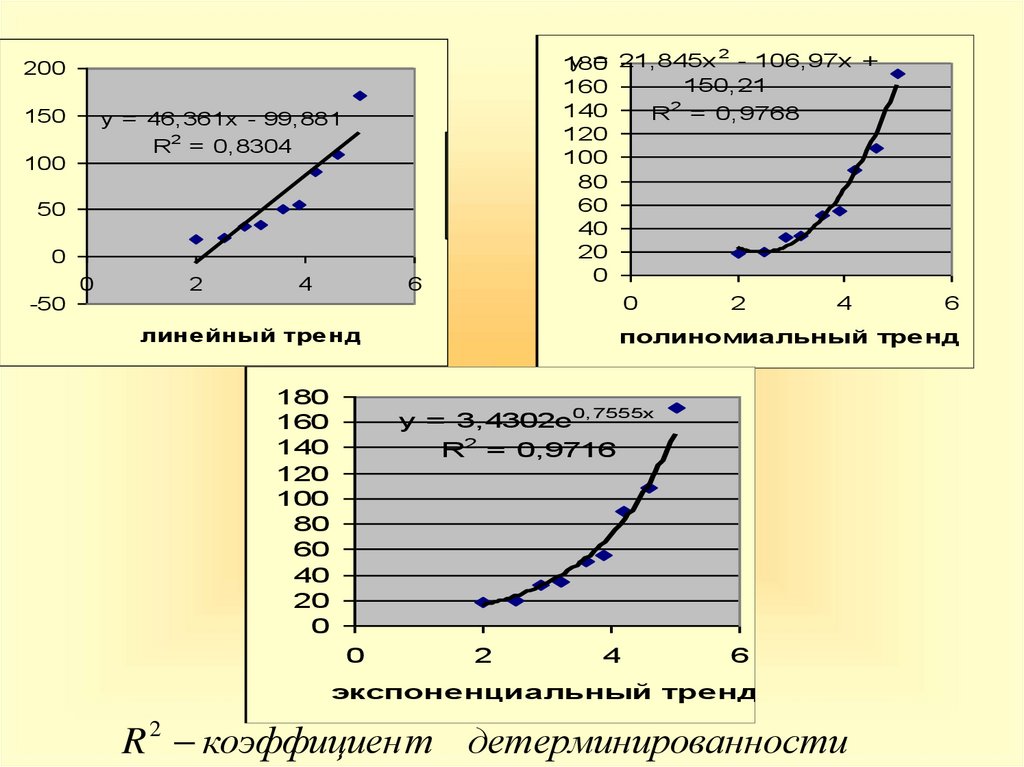
линейный тренд
180
160
140
120
100
80
60
40
20
0
6
полиномиальный тренд
y = 3,4302e0,7555x
R2 = 0,9716
Ряд1
Экспоненци
альный
(Ряд1)
0
2
4
6
экспоненциальный тренд
R 2 коэффициен т детерминированности
12.
200150
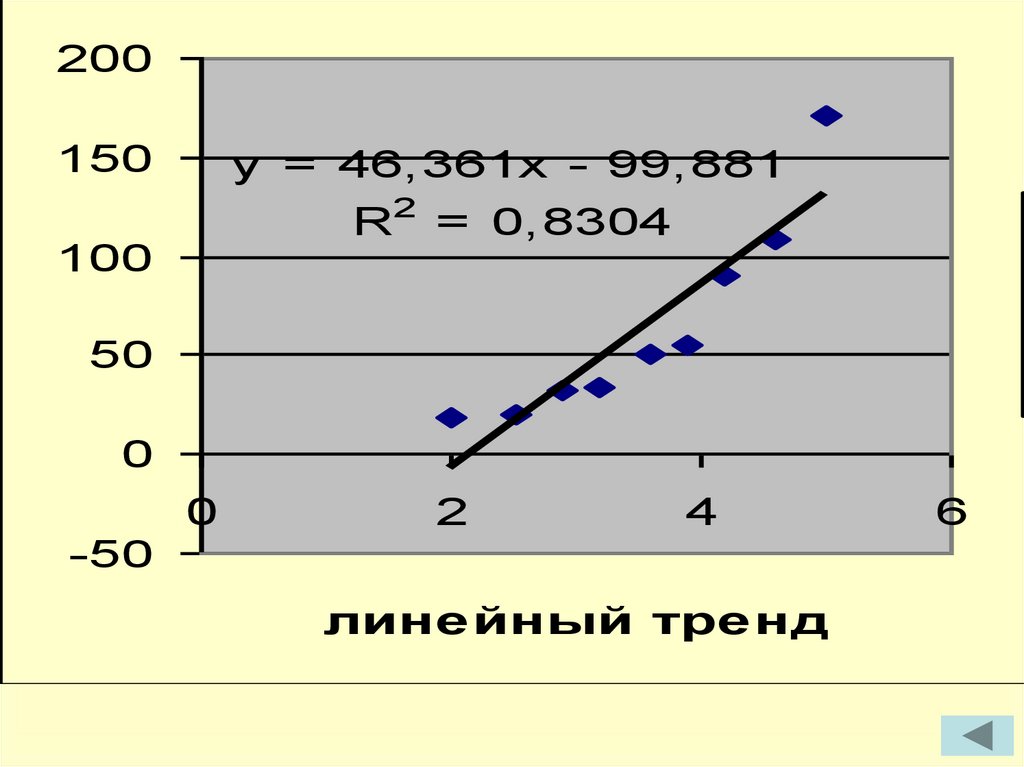
y = 46,361x - 99,881
R2 = 0,8304
100
50
0
-50
0
2
4
линейный тренд
6
13.
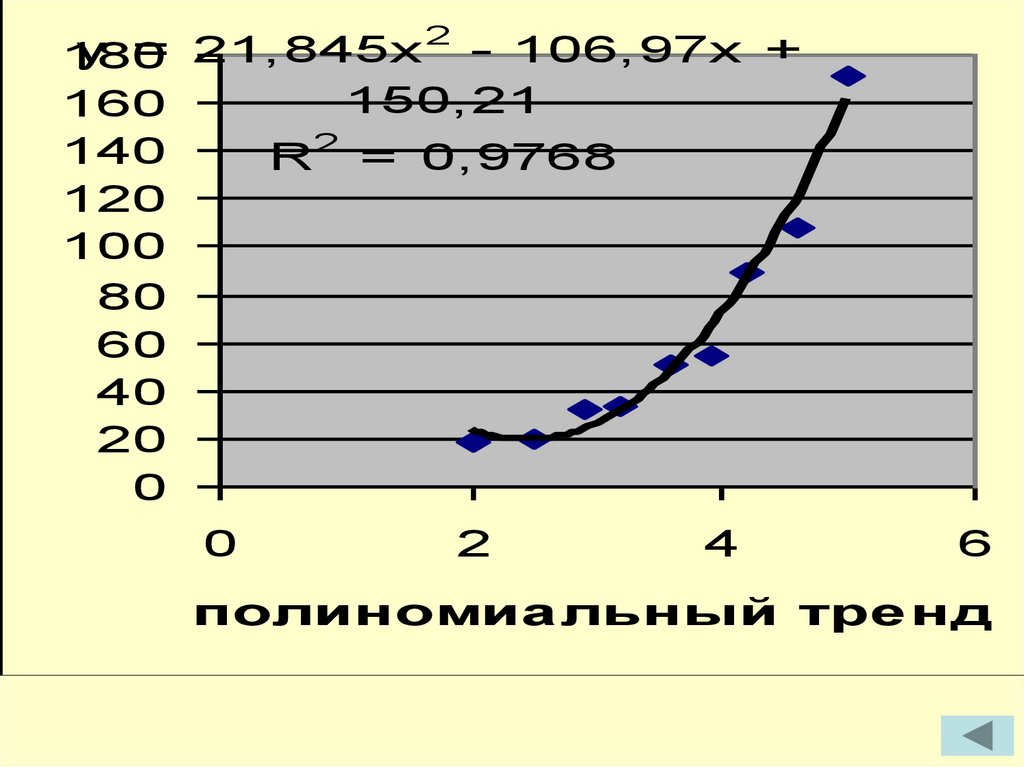
2y
=
21,845x
- 106,97x +
180
150,21
160
2
140
R = 0,9768
120
100
80
60
40
20
0
0
2
4
6
полиномиа льный тре нд
14.
180160
140
120
100
80
60
40
20
0
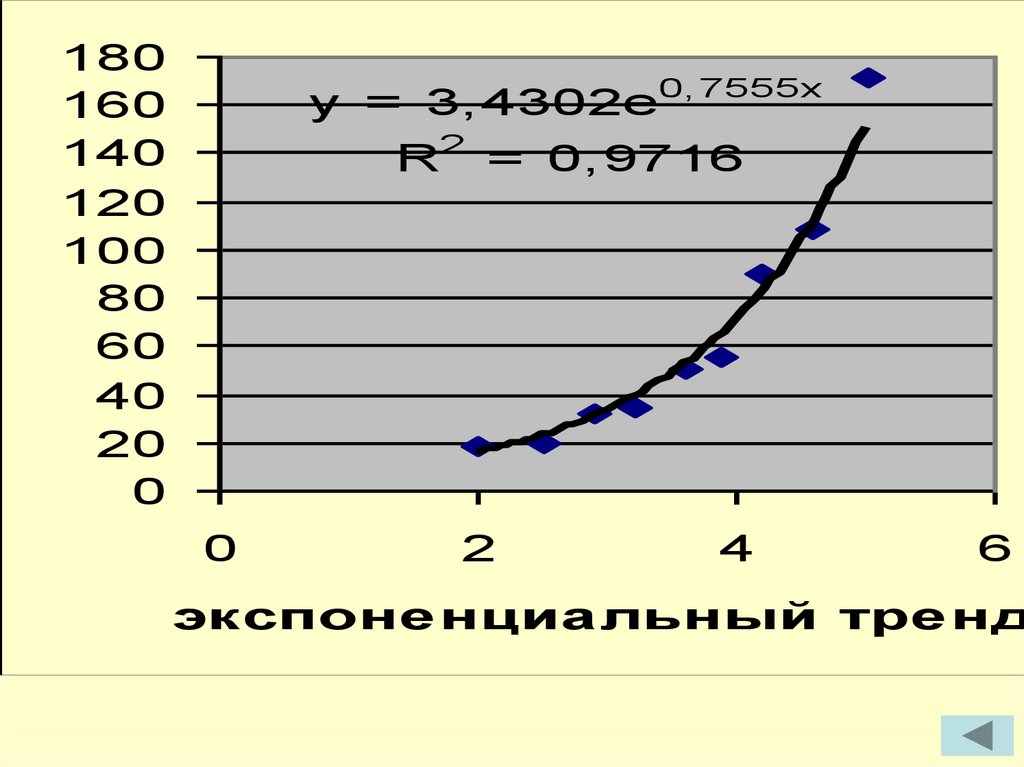
y = 3,4302e0,7555x
R2 = 0,9716
0
2
4
6
экспоне нциа льный тре нд







 Математика
Математика








