Похожие презентации:
Системы и совокупности неравенств с одной переменной
1. Системы и совокупности.
22.04.2.
Понятие система – совокупностьСистема
Символика
Словесная
интерпретация
А
В
А В
пересечение
Необходимо
выполнение двух
условий: и условия А,
и условия В.
Совокупность
А
В
А В
объединение
Достаточно
выполнения хотя бы
одного из условий: или
А, или В.
Схема
22.04.2021
2
3.
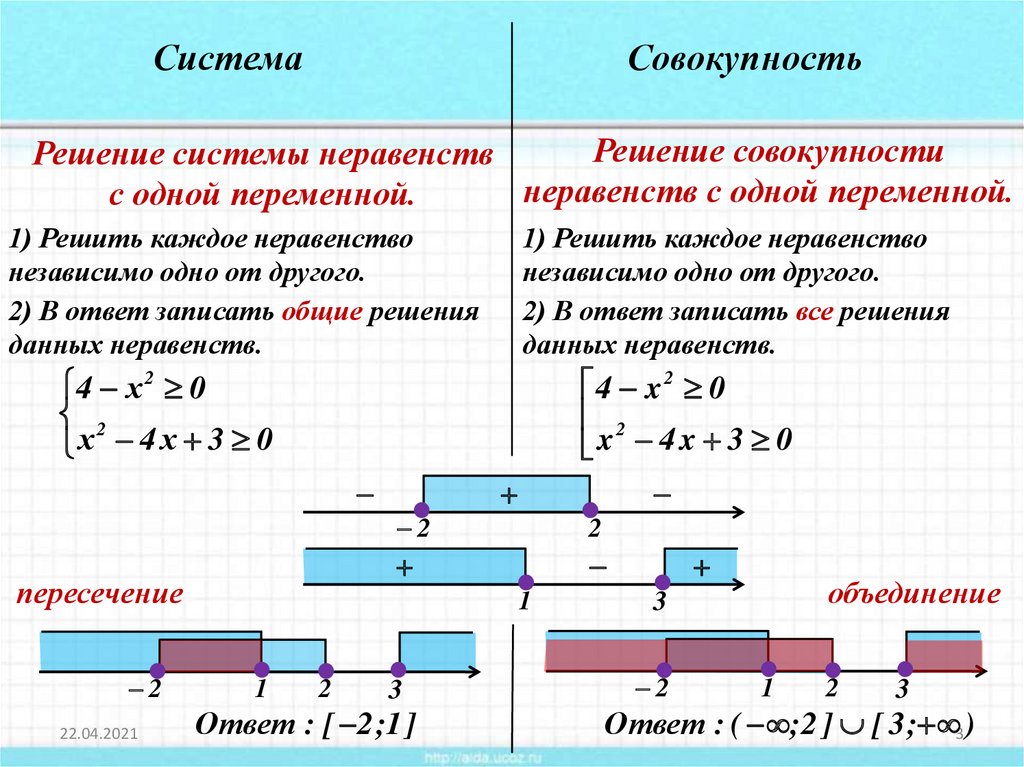
СистемаСовокупность
Решение совокупности
Решение системы неравенств
неравенств с одной переменной.
с одной переменной.
1) Решить каждое неравенство
независимо одно от другого.
2) В ответ записать общие решения
данных неравенств.
1) Решить каждое неравенство
независимо одно от другого.
2) В ответ записать все решения
данных неравенств.
4 х 2 0
2
х 4 х 3 0
22.04.2021
2
пересечение
2
2
4 x 2 0
2
x 4 x 3 0
1
1
2
3
Ответ : [ 2 ;1 ]
объединение
3
2
1
2
3
Ответ : ( ;2 ] [ 3 ; 3)
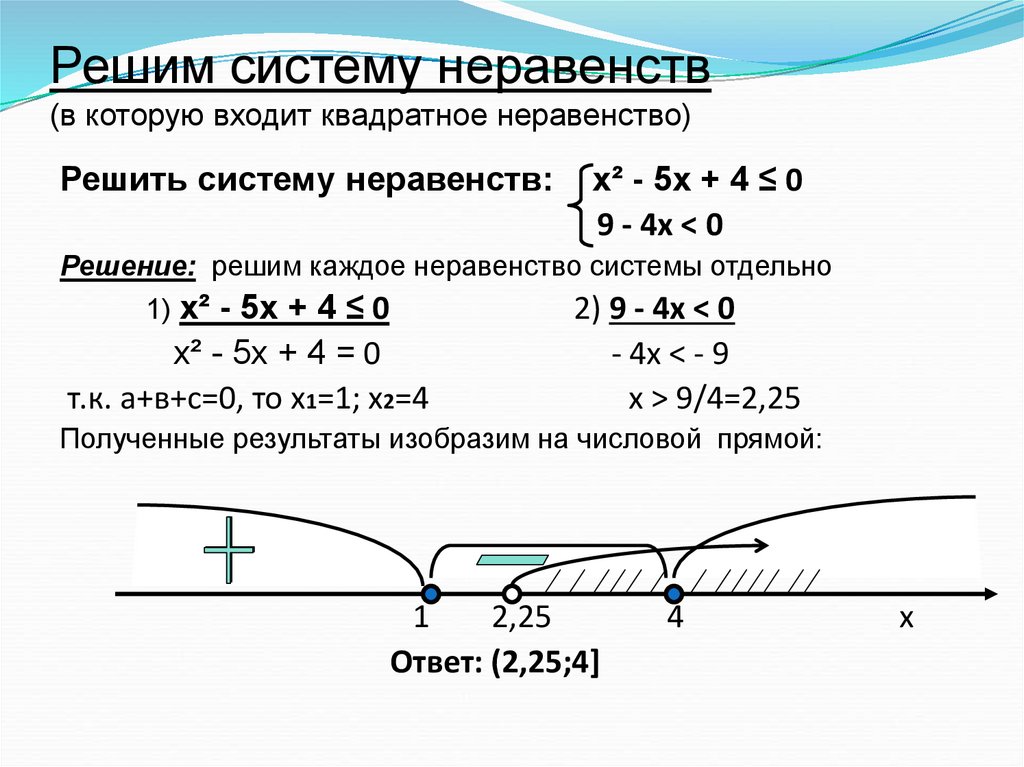
4. Решим систему неравенств (в которую входит квадратное неравенство)
Решить систему неравенств:х² - 5х + 4 ≤ 0
9 - 4х < 0
Решение: решим каждое неравенство системы отдельно
1) х² - 5х + 4 ≤ 0
х² - 5х + 4 = 0
т.к. а+в+с=0, то х1=1; х2=4
2) 9 - 4х < 0
- 4х < - 9
х > 9/4=2,25
Полученные результаты изобразим на числовой прямой:
1
2,25
Ответ: (2,25;4]
4
х
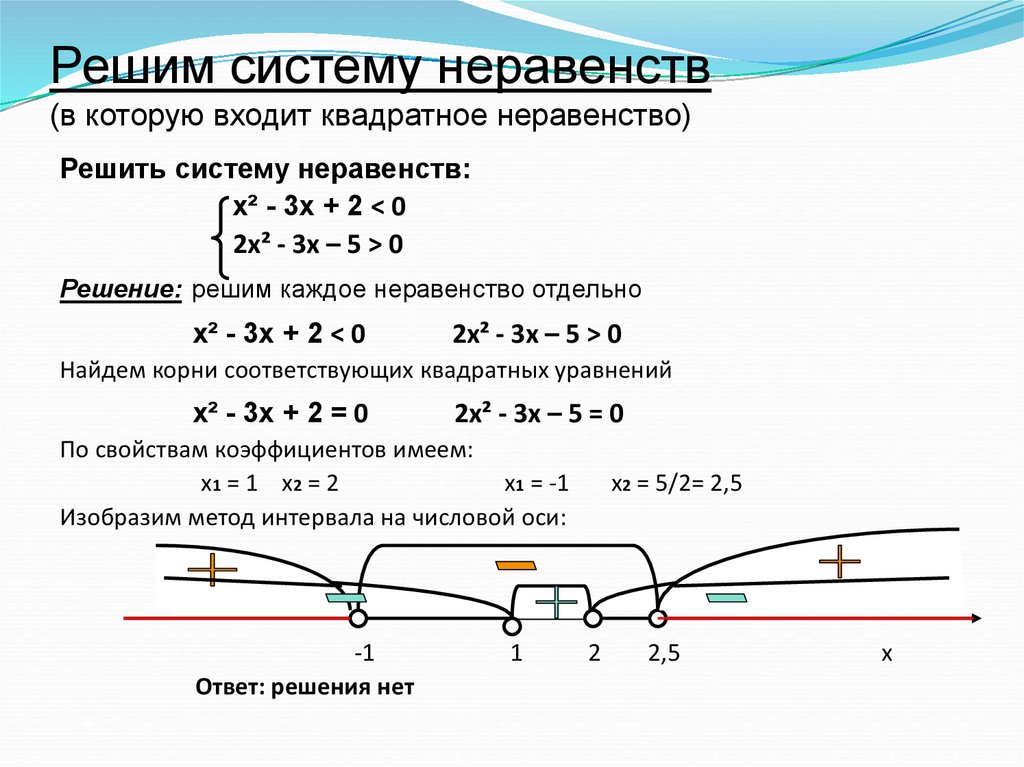
5. Решим систему неравенств (в которую входит квадратное неравенство)
Решить систему неравенств:х² - 3х + 2 < 0
2х² - 3х – 5 > 0
Решение: решим каждое неравенство отдельно
х² - 3х + 2 < 0
2х² - 3х – 5 > 0
Найдем корни соответствующих квадратных уравнений
х² - 3х + 2 = 0
2х² - 3х – 5 = 0
По свойствам коэффициентов имеем:
х1 = 1 х 2 = 2
х1 = -1
Изобразим метод интервала на числовой оси:
-1
Ответ: решения нет
1
х2 = 5/2= 2,5
2
2,5
х
6.
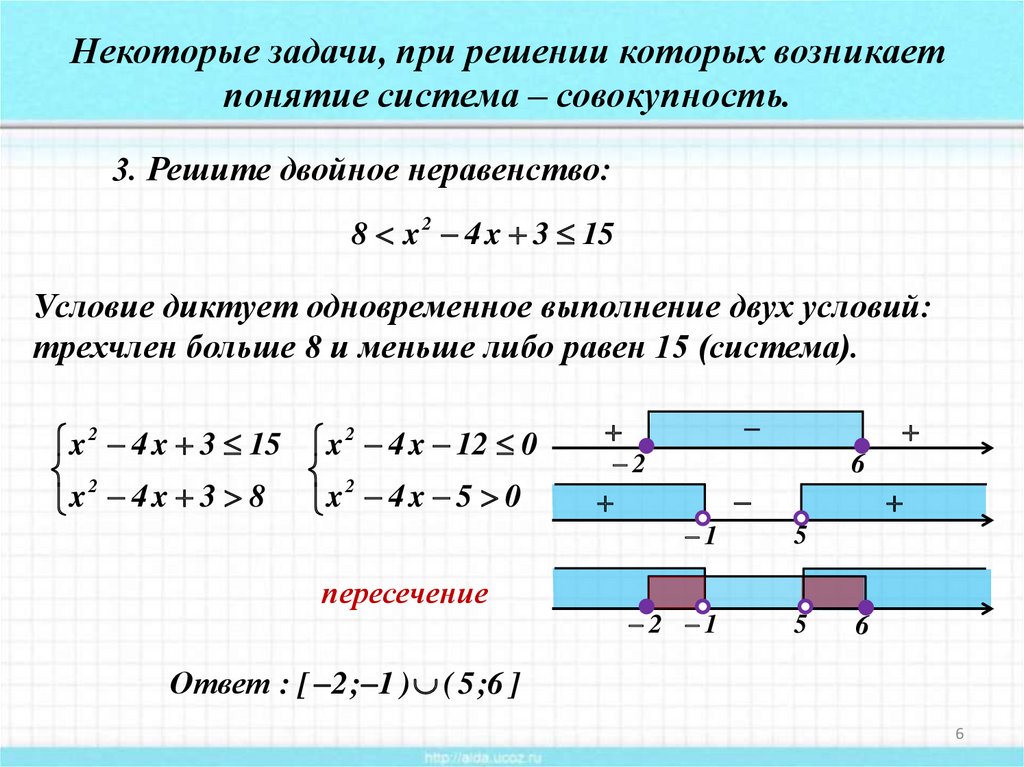
Некоторые задачи, при решении которых возникаетпонятие система – совокупность.
3. Решите двойное неравенство:
8 x 2 4 x 3 15
Условие диктует одновременное выполнение двух условий:
трехчлен больше 8 и меньше либо равен 15 (система).
x 4 x 3 15 x 4 x 12 0
2
2
x 4 x 3 8 x 4 x 5 0
2
2
пересечение
_
2
6
1
2 1
5
5
6
Ответ : [ 2 ; 1 ) ( 5 ;6 ]
6
7.
Некоторые задачи, при решении которых возникаетпонятие система – совокупность.
4. Решите неравенство методом замены переменной:
Замена : x 2 4 t
2( x 2 4 )2 3( x 2 4 ) 1 0
2 t 2 3t 1 0
1
2
1
t ; ( 1; ) - совокупность.
2
3
1 2 9
1 2
2
t 2 x 4 2 x 2 0
2
2
t
1
x
4
1
x
5
0
объединение
Ответ : ; 5
5 ;
1
_
3
2
5
5
5
5
8.
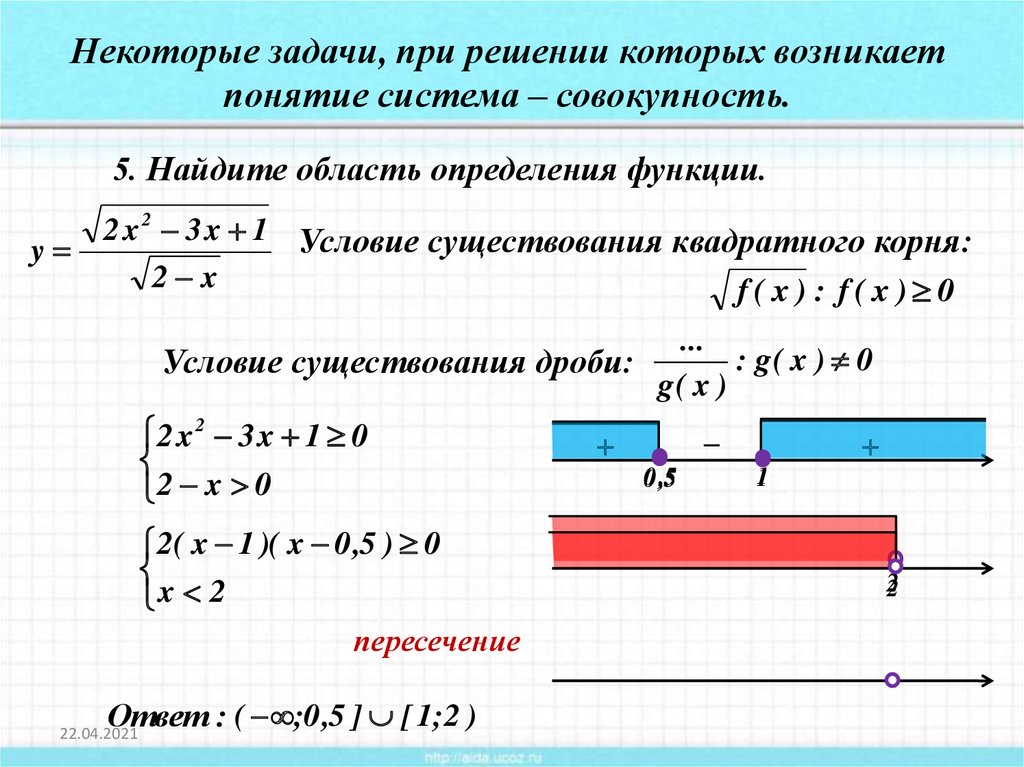
Некоторые задачи, при решении которых возникаетпонятие система – совокупность.
5. Найдите область определения функции.
y
2 x 2 3 x 1 Условие существования квадратного корня:
2 x
f( x) : f( x) 0
...
: g( x ) 0
Условие существования дроби:
g( x )
2 x 2 3 x 1 0
2 x 0
2( x 1 )( x 0 ,5 ) 0
x 2
пересечение
Ответ : ( ;0 ,5 ] [ 1;2 )
22.04.2021
_
0 ,5
1
22
9. Домашнее задание решите системы неравенств
1) 6х² - 5х + 1 > 04х – 1 ≥ 0
3) х² - 10х + 9 ≥ 0
12 – 3х < 0
2) 4х² - 1 ≤ 0
х² > 1
4) 2х²- 5х + 2 > 0
4х – 1 ≥ 3





 Математика
Математика








