Похожие презентации:
Кеңістіктегі жазықтық пен түзудің теңдеулері
1.
Алгебра және геометрияКеңістіктегі жазықтық пен
түзудің теңдеулері
2.
1. Жазықтықтың теңдеуіЖазықтықта P x0 , y0 , z0 нүктесі және жазықтыққа
перпендикуляр болатын n A, B, C векторы берілсін.
M x, y, z жазықтықтың кез
келген нүктесі
PM n PM n 0
PM x x0 , y y0 , z z0
n A, B, C
A x x0 B y y0 C z z0 0
(1)
(1) – берілген P x0 , y0 , z0 нүктесі арқылы өтетін n A, B, C
векторына перпендикуляр жазықтықтың теңдеуі.
3.
Мысал. M 0 (1;2;1) нүктесінен өтетін және n 2;3; 4векторына перпендикуляр болып өтетін жазықтықтың
теңдеуін жазыңыз.
Шешімі: (1) теңдеуді пайдалансақ
2 x 1 3 y 2 4 z 1 0
2x 3y 4z 4 0
4.
A x x0 B y y0 C z z0 0теңдеуін түрлендіріп
Ax By Cz D 0
(2) – жазықтықтың жалпы теңдеуі, мұндағы
D Ax0 By 0 Cz0 .
(2)
5.
Жалпы теңдеуінің кейбір дербес жағдайлары:Ax By Cz D 0
D 0 Ax By Cz 0
жазықтығы координата
жүйесінің бас нүктесінен өтеді.
C 0 Ax By D 0
параллель болады.
жазықтығы Oz осіне
D
жазықтығы
A
OYZ координаталық жазықтығына параллель болады.
B 0, C 0
Ax D 0 немесе
x
B 0, C 0, D 0 Ax 0, x 0 теңдеуі OYZ
координаталық жазықтығының теңдеуі болады.
6.
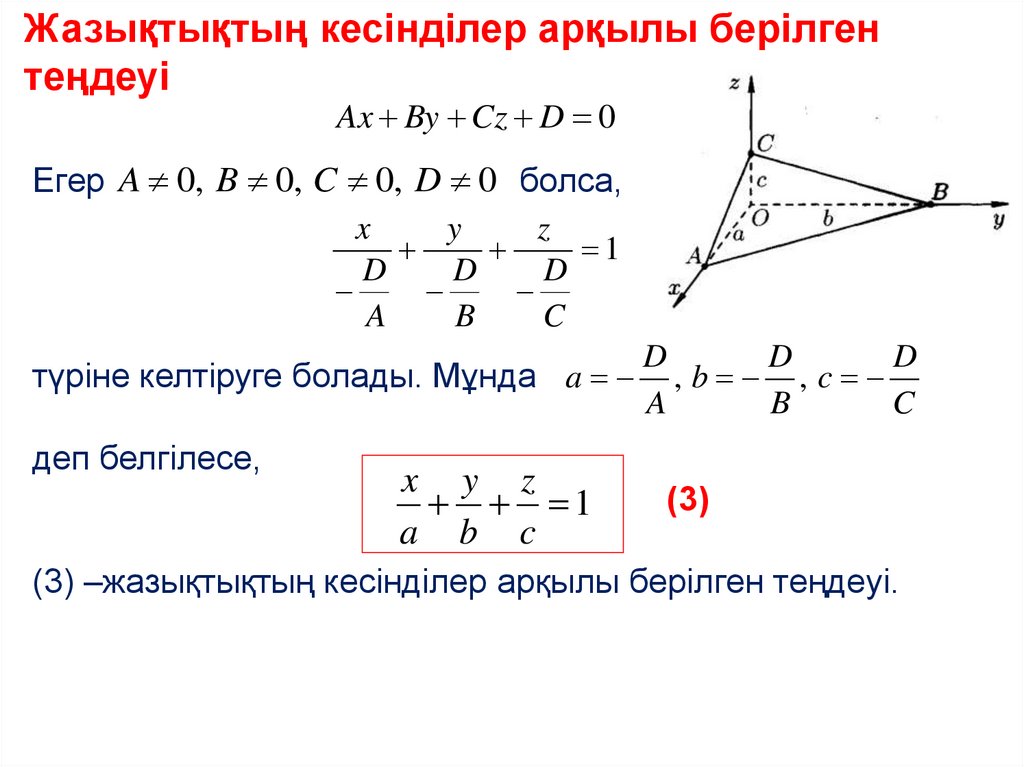
Жазықтықтың кесінділер арқылы берілгентеңдеуі
Ax By Cz D 0
Егер A 0, B 0, C 0, D 0 болса,
x
y
z
1
D
D
D
A
B
C
D
D
D
түріне келтіруге болады. Мұнда a , b , c
A
B
C
деп белгілесе,
x y z
1
a b c
(3)
(3) –жазықтықтың кесінділер арқылы берілген теңдеуі.
7.
Үш нүкте арқылы өтетін жазықтықтың теңдеуіКеңістікте M1 x1 , y1 , z1 , M 2 x2 , y2 , z2 , M 3 x3 , y3 , z3 нүктелері
берілсін. Осы нүктелер арқылы өтетін жазықтықтың теңдеуін
табу үшін жазықтықта жатқан кез келген M x, y, z нүктесін
алайық. Онда M 1M , M 1M 2 , M 1M 3 векторлары компланар
векторлар.
M 1M x x1 , y y1 , z z1 ,
M 1M 2 x2 x1 , y2 y1 , z2 z1 ,
M 1M 3 x3 x1 , y3 y1 , z3 z1
M 1M M 1M 2 M 1M 3 0
x x1
y y1
z z1
x2 x1
y2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
(4)
(4) - үш нүкте арқылы өтетін жазықтықтың теңдеуі
8.
Нүктеден жазықтыққа дейінгі арақашықтықКеңістікте M 0 x0 , y0 , z0 нүктесінен Ax By Cz D 0
жазықтығына дейінгі арақашықтығын келесі формуламен
табылады:
Ax0 By 0 Cz0 D
d
(5)
2
2
2
A B C
9.
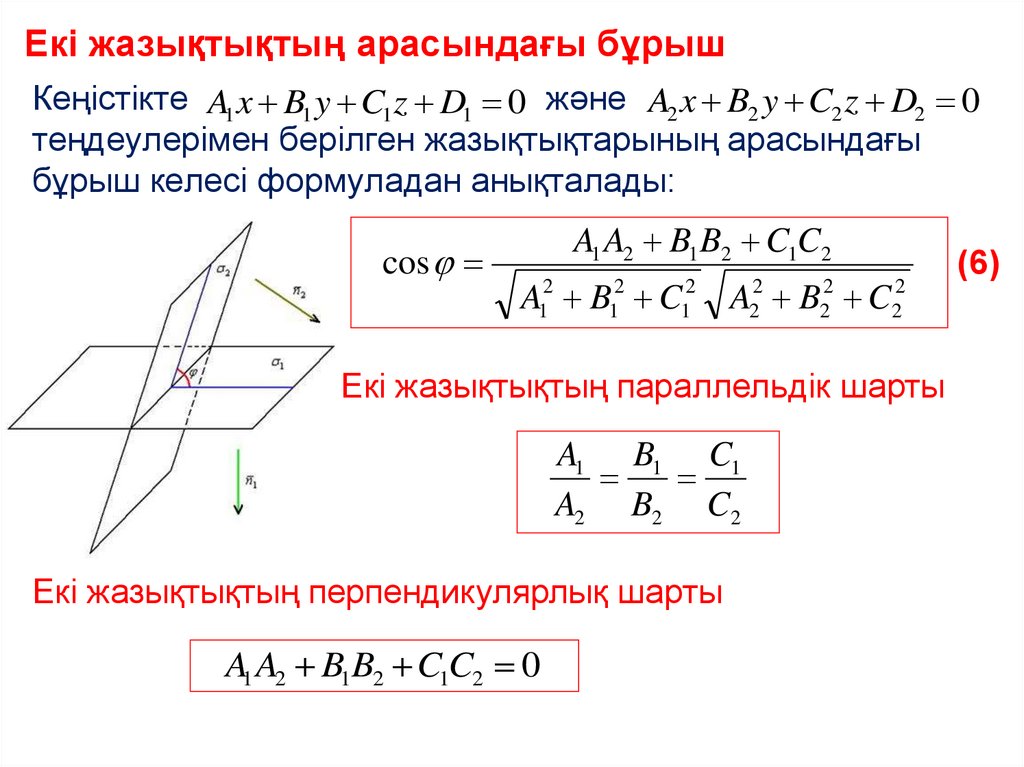
Екі жазықтықтың арасындағы бұрышКеңістікте A1 x B1 y C1 z D1 0 және A2 x B2 y C2 z D2 0
теңдеулерімен берілген жазықтықтарының арасындағы
бұрыш келесі формуладан анықталады:
cos
A1 A2 B1 B2 C1C2
A B C
2
1
2
1
2
1
A B C
2
2
2
2
2
2
Екі жазықтықтың параллельдік шарты
A1 B1 C1
A2 B2 C2
Екі жазықтықтың перпендикулярлық шарты
A1 A2 B1B2 C1C2 0
(6)
10.
Кеңістіктегі түзудің канондық теңдеуіM 0 x0 , y0 , z0 нүкте және
Айталық , түзуде
осы түзуге
параллель a m, n, p векторы берілсін. a - түзудің
бағыттаушы векторы деп аталады. Түзуден кез келген
M x, y, z нүктесін алайық. Онда
M 0 M || a.
M 0 M x x0 , y y0 , z z0 , a m, n, p
x x0 y y0 z z0
m
n
p
(7) - кеңістіктегі түзудің канондық теңдеуі.
(7)
11.
Кеңістіктегі түзудің параметрлік теңдеуіКеңістіктегі түзудің канондық теңдеуі берілсін
x x0 y y0 z z0
m
n
p
x x0 y y0 z z0
t
m
n
p
x x0
m t
x x0 mt
y y0
t
(8)
y y0 nt
n
z z pt
0
z z0
p t
(8) - кеңістіктегі түзудің параметрлік теңдеуі
12.
Кеңістіктегі екі нүкте арқылы өтетін түзудің теңдеуіКеңістіктегі M1 x1 , y1 , z1 , M 2 x2 , y2 , z2 нүктелері арқылы
өтетін түзудің теңдеуін жазайық.
a M1M 2 x2 x1 , y2 y1 , z2 z1
векторын осы түзудің бағыттаушы
векторы деп алсақ, онда M1
нүктесі арқылы өтетін теңдеуді
(7) теңдеу арқылы
x x1
y y1
z z1
(9)
x2 x1 y2 y1 z 2 z1
аламыз. Бұл теңдеу екі нүкте арқылы өтетін түзудің теңдеуі
деп аталады.
13.
Кеңістіктегі екі түзудің арасындағы бұрышКеңістіктегі
x x1 y y1 z z1
m1
n1
p1
x x2 y y 2 z z 2
m2
n2
p2
және
теңдеулерімен анықталатын екі түзудің
арасындағы бұрыш келесі формуладан
табылады:
cos
m1m2 n1n2 p1 p2
m n p
2
1
2
1
2
1
m n p
2
2
2
2
2
2
(10)
14.
Кеңістіктегі түзулердің параллельдік шартыm1 n1 p1
m2 n2 p2
(11)
Кеңістіктегі түзулердің перпендикулярлық шарты
m1m2 n1n2 p1 p2 0
(12)
15.
Жазықтық пен түзудің арасындағы бұрышКеңістікте Ax By Cz D 0 теңдеуімен берілген
жазықтық пен
x x0 y y0 z z0
m
n
p
теңдеуімен берілген түзудің арасындағы бұрыш келесі
формула арқылы табылады:
sin
Am Bn Cp
A2 B 2 C 2 m 2 n 2 p 2
Жазықтық пен түзудің параллельдік
шарты
Am Bn Cp 0
Жазықтық пен түзудің перпендикулярлық шарты
A B C
m n p
(13)













 Математика
Математика








