Похожие презентации:
Площади и объемы многогранников. Решение задач
1.
Презентация для урока геометрии в 11 классе.Тема: Решение задач по теме «Площади и объемы
многогранников».
Автор:
Асмус О.В.
- зам. директора по УВР,
учитель математики
2.
Классная работа.3.
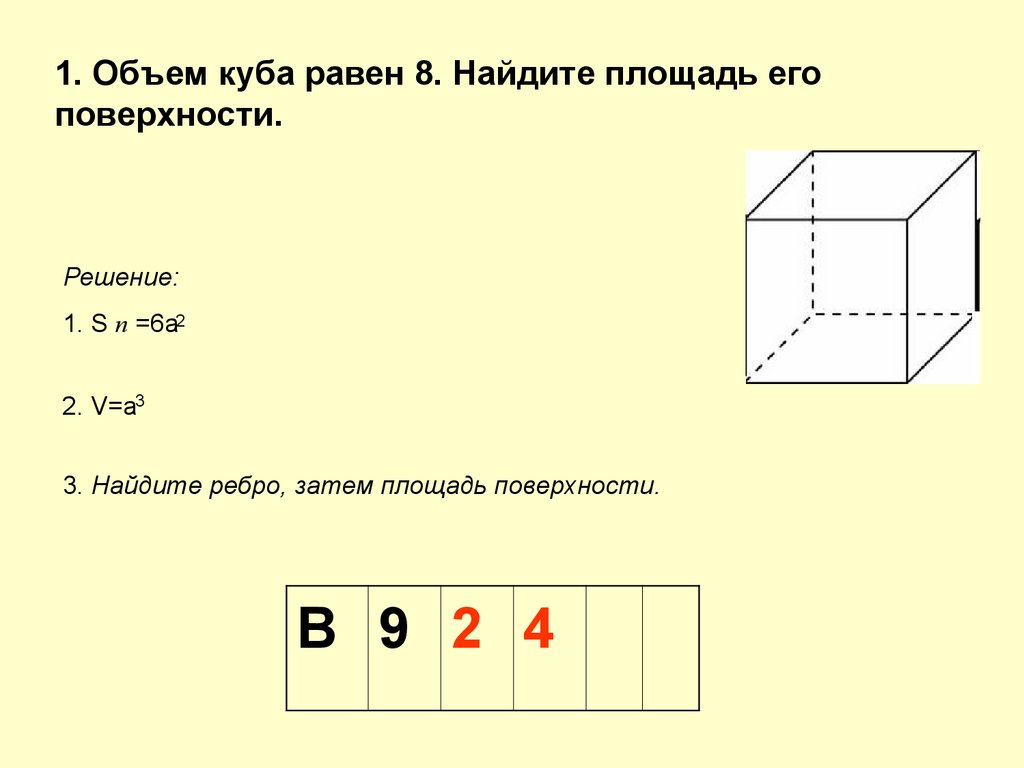
1. Объем куба равен 8. Найдите площадь егоповерхности.
Решение:
1. S п =6а2
2. V=а3
3. Найдите ребро, затем площадь поверхности.
В 9 2 4
4.
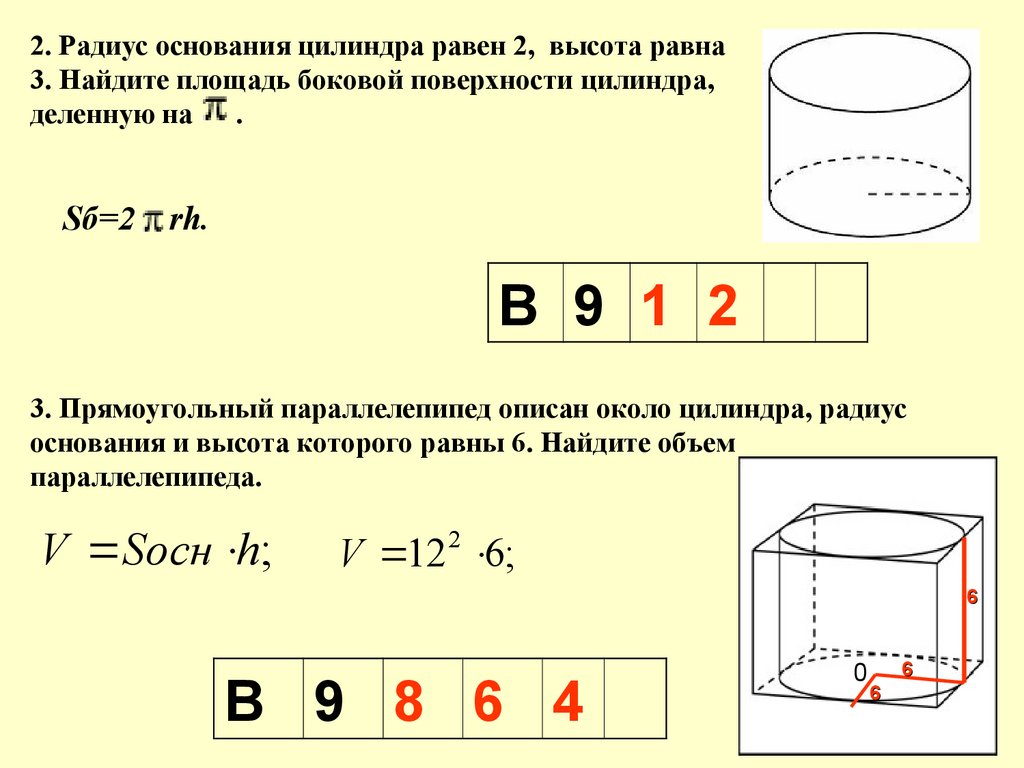
2. Радиус основания цилиндра равен 2, высота равна3. Найдите площадь боковой поверхности цилиндра,
деленную на
.
Sб=2
rh.
В 9 1 2
3. Прямоугольный параллелепипед описан около цилиндра, радиус
основания и высота которого равны 6. Найдите объем
параллелепипеда.
V Sосн h;
V 12 2 6;
6
В 9 8 6 4
0
6
6
5.
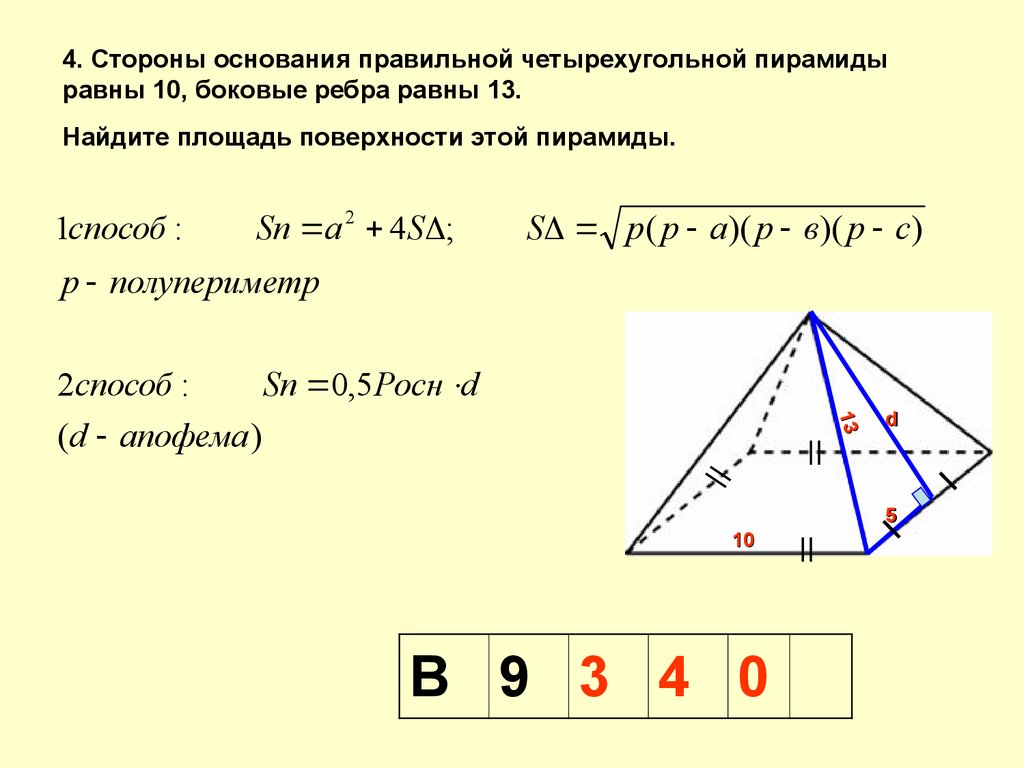
4. Стороны основания правильной четырехугольной пирамидыравны 10, боковые ребра равны 13.
Найдите площадь поверхности этой пирамиды.
1способ :
Sп а 2 4 S ;
S р ( р а )( р в )( р с)
р полупериметр
13
2способ :
Sп 0,5 Росн d
(d апофема )
d
5
10
В 9 3 4 0
6.
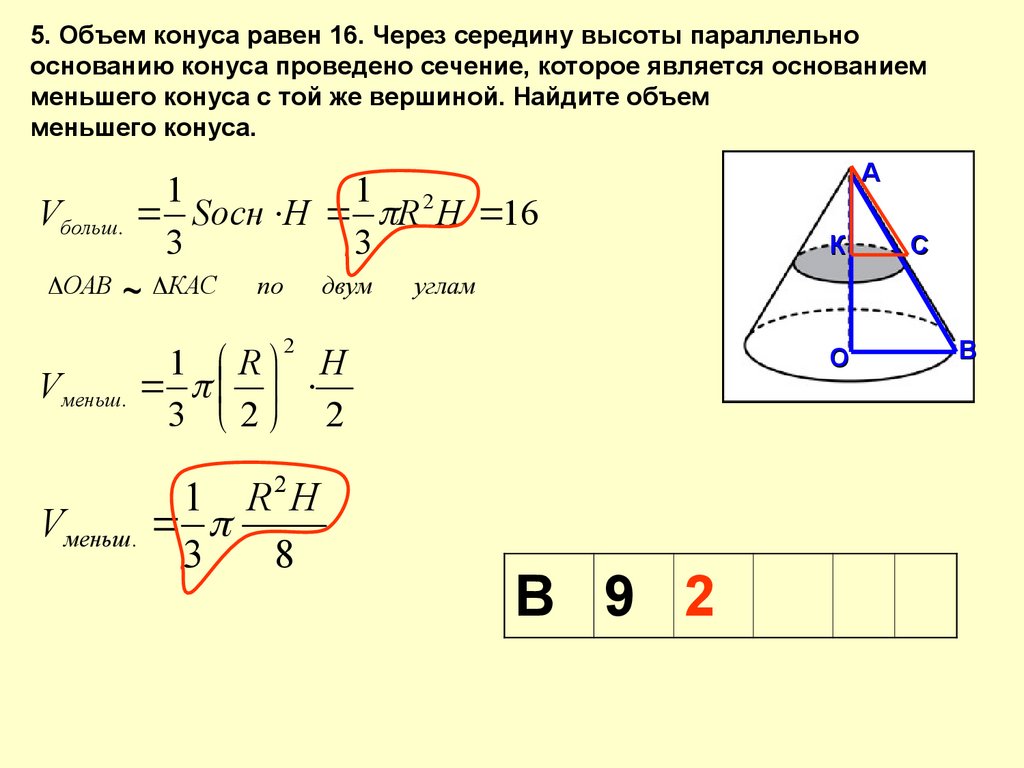
5. Объем конуса равен 16. Через середину высоты параллельнооснованию конуса проведено сечение, которое является основанием
меньшего конуса с той же вершиной. Найдите объем
меньшего конуса.
Vбольш.
ОАВ
1
1 2
Sосн Н R H 16
3
3
~
КАС
по
двум
Vменьш.
Vменьш.
1 R2H
3
8
К
С
углам
2
1 R H
3 2 2
А
О
В 9 2
В
7.
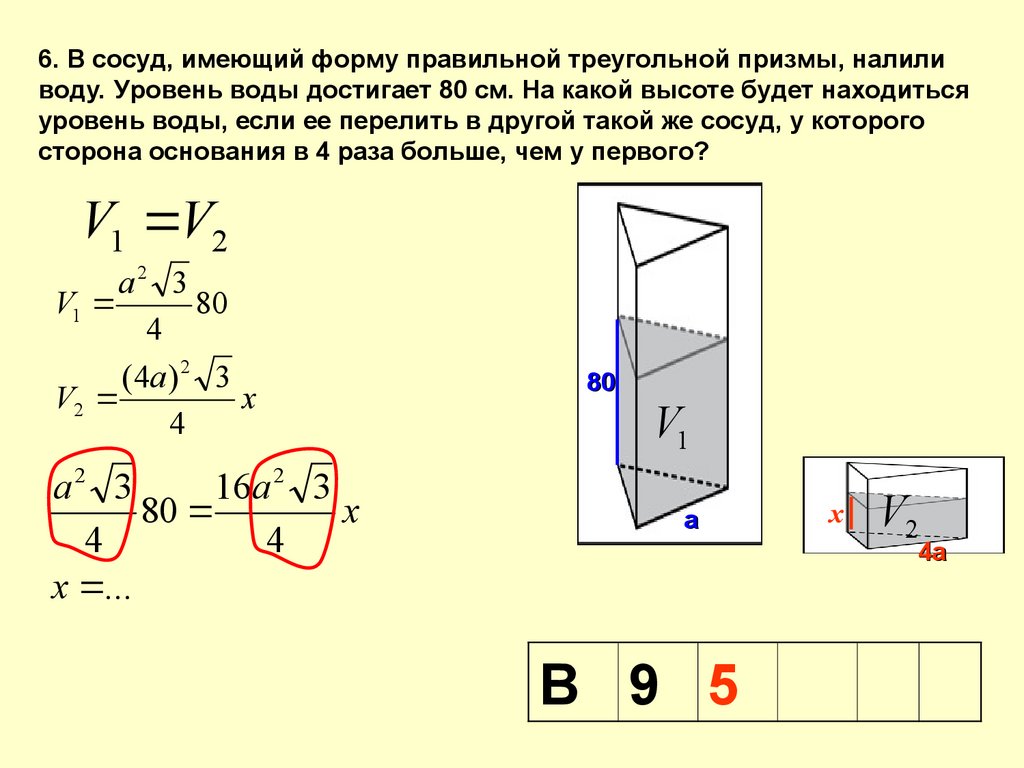
6. В сосуд, имеющий форму правильной треугольной призмы, налиливоду. Уровень воды достигает 80 см. На какой высоте будет находиться
уровень воды, если ее перелить в другой такой же сосуд, у которого
сторона основания в 4 раза больше, чем у первого?
V1 V2
a2 3
V1
80
4
( 4a ) 2 3
V2
x
4
a2 3
16a 2 3
80
x
4
4
x ...
80
V1
а
х
V2
4а
В 9 5
8.
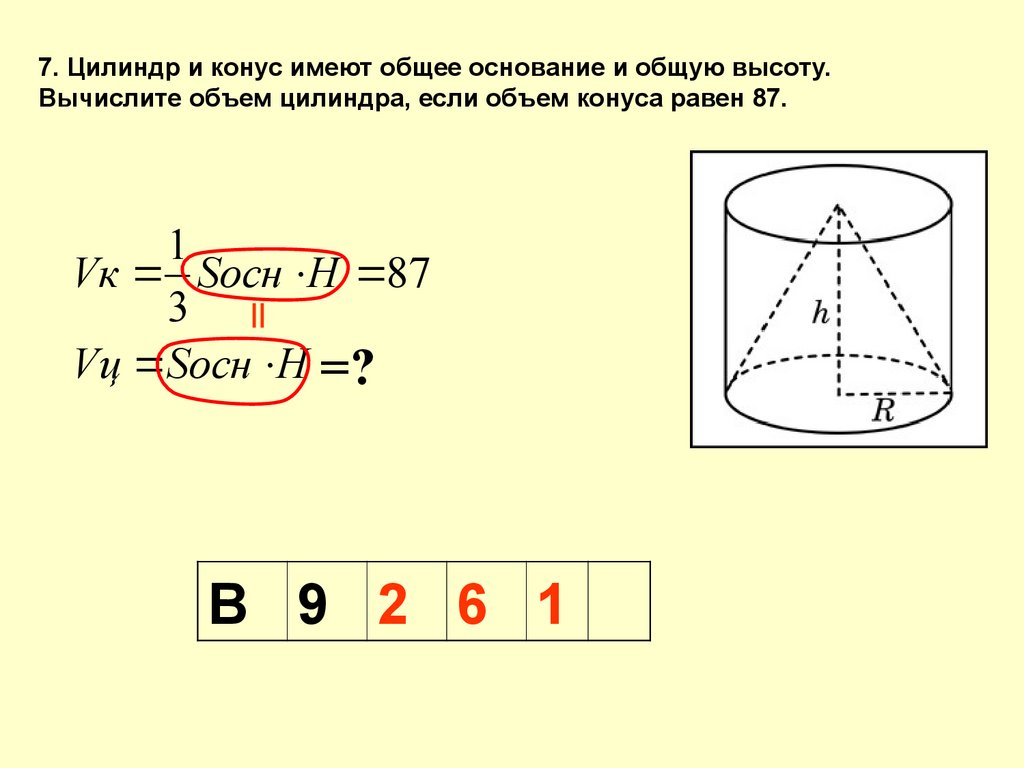
7. Цилиндр и конус имеют общее основание и общую высоту.Вычислите объем цилиндра, если объем конуса равен 87.
1
Vк Sосн Н 87
3
Vц Socн H =?
В 9 2 6 1
9.
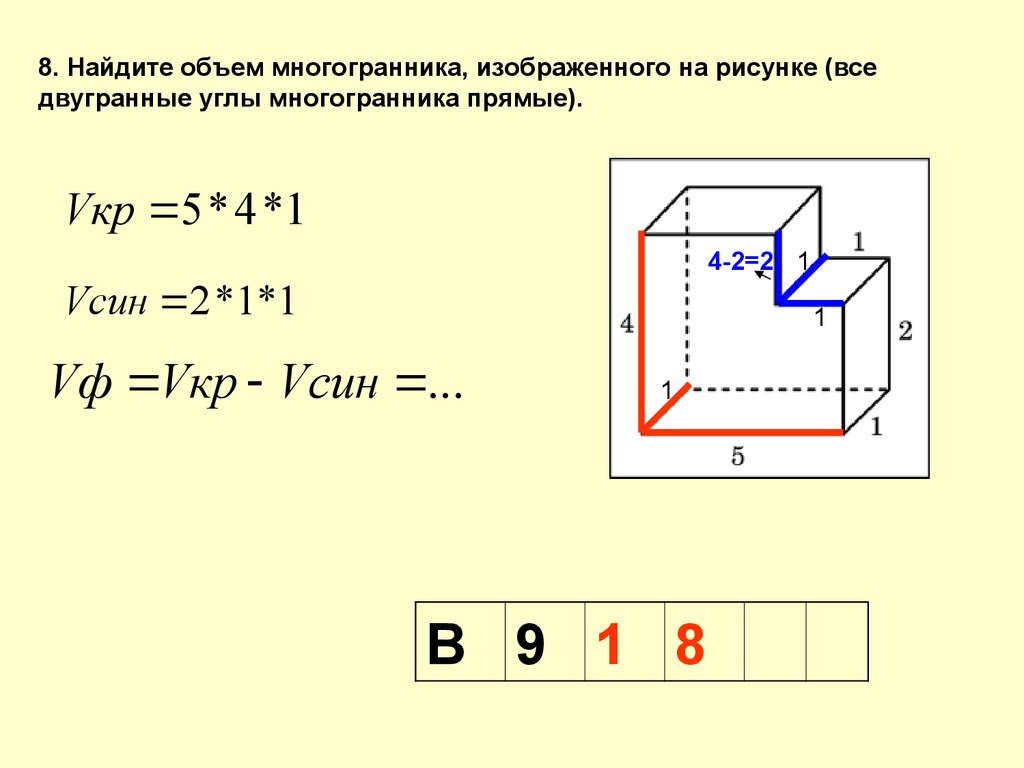
8. Найдите объем многогранника, изображенного на рисунке (вседвугранные углы многогранника прямые).
Vкр 5 * 4 *1
4-2=2 1
Vсин 2 *1*1
1
Vф Vкр Vсин ...
1
В 9 1 8
10.
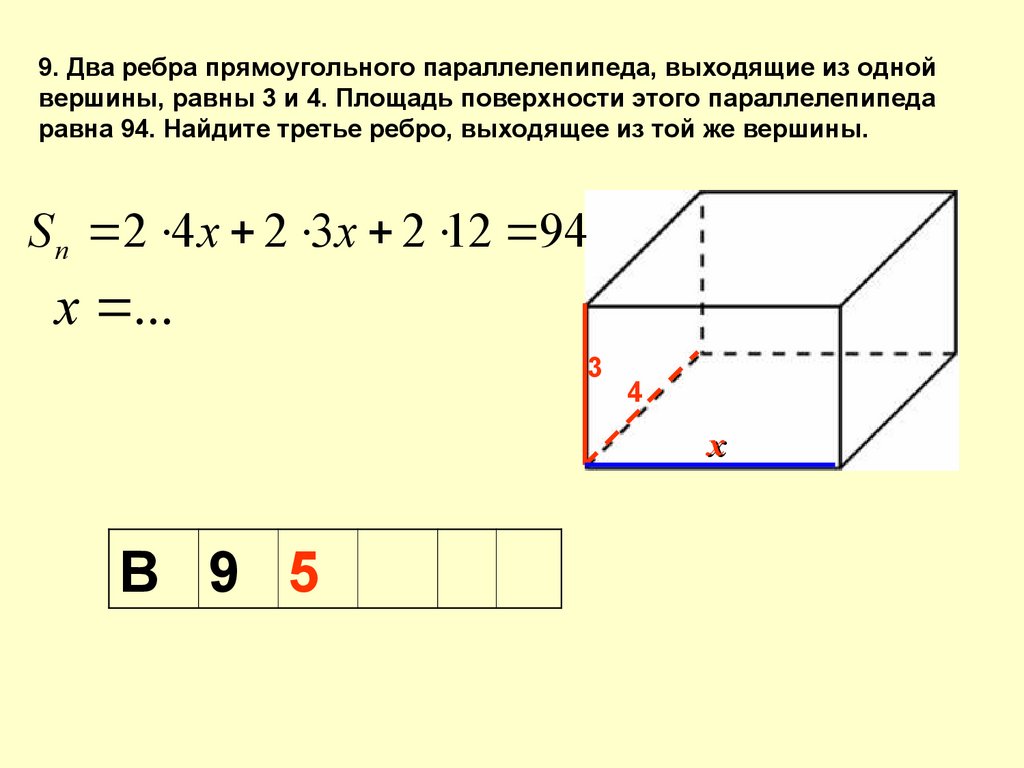
9. Два ребра прямоугольного параллелепипеда, выходящие из однойвершины, равны 3 и 4. Площадь поверхности этого параллелепипеда
равна 94. Найдите третье ребро, выходящее из той же вершины.
S п 2 4 х 2 3 х 2 12 94
х ...
3
4
х
В 9 5
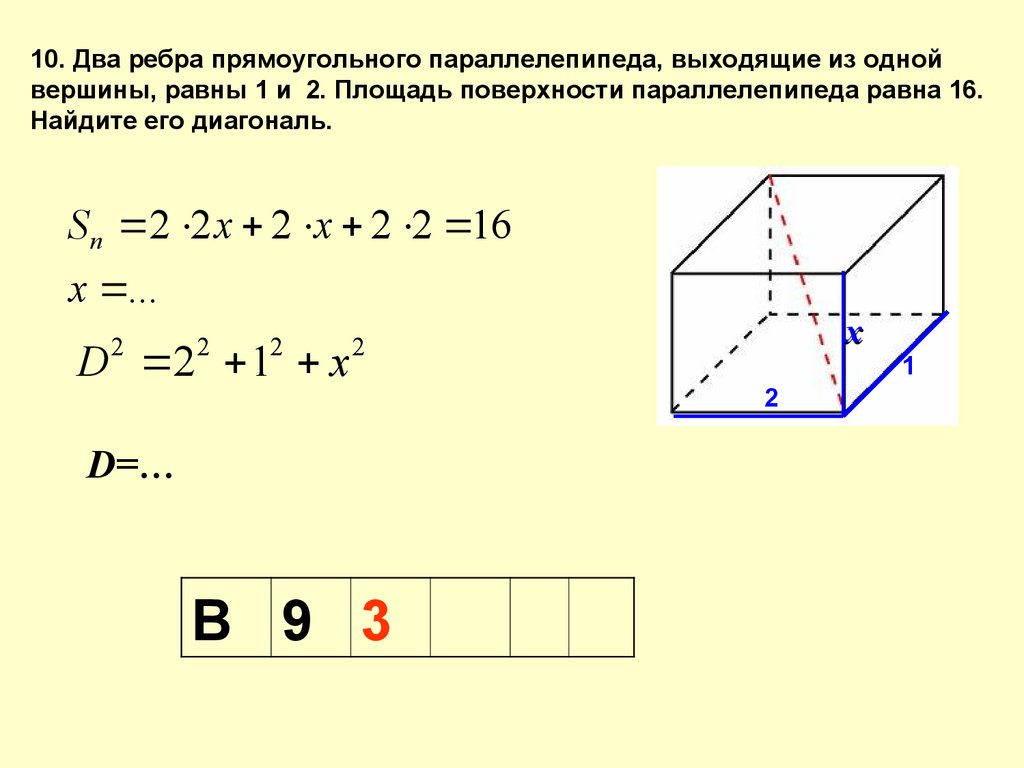
11.
10. Два ребра прямоугольного параллелепипеда, выходящие из однойвершины, равны 1 и 2. Площадь поверхности параллелепипеда равна 16.
Найдите его диагональ.
S п 2 2 х 2 х 2 2 16
х ...
2
2
2
D 2 1 x
х
2
D=…
В 9 3
2
1
12.
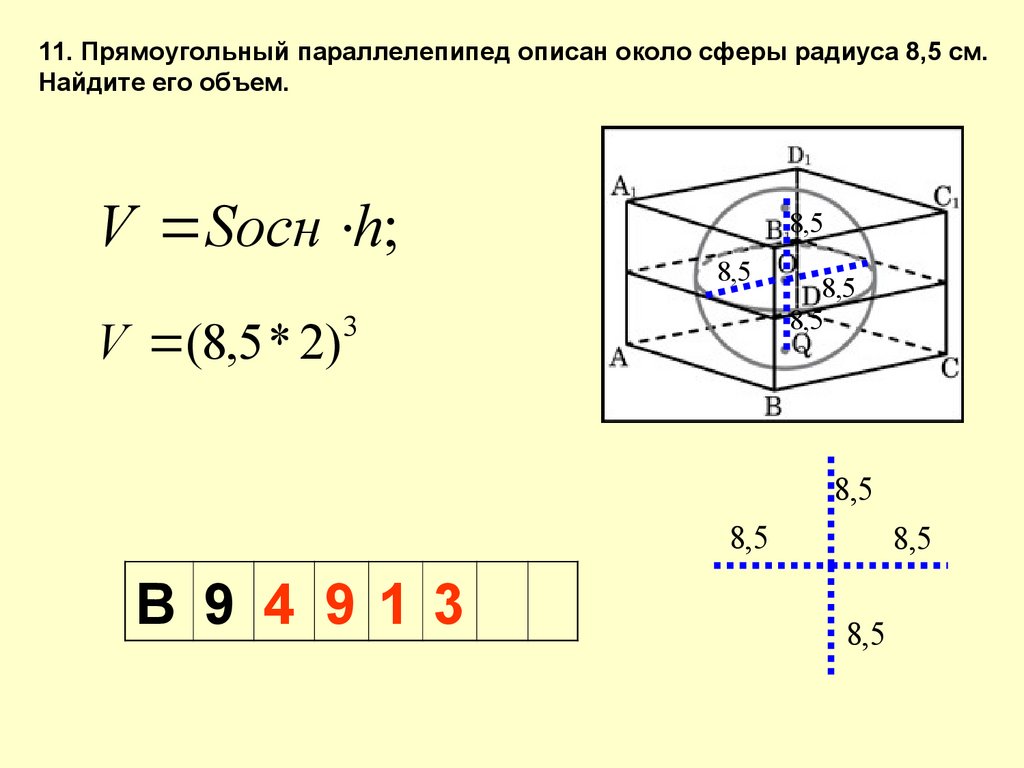
11. Прямоугольный параллелепипед описан около сферы радиуса 8,5 см.Найдите его объем.
V Sосн h;
V (8,5 * 2)
8,5
8,5
3
8,5
8,5
8,5
8,5
В 9 4 913
8,5
8,5
13.
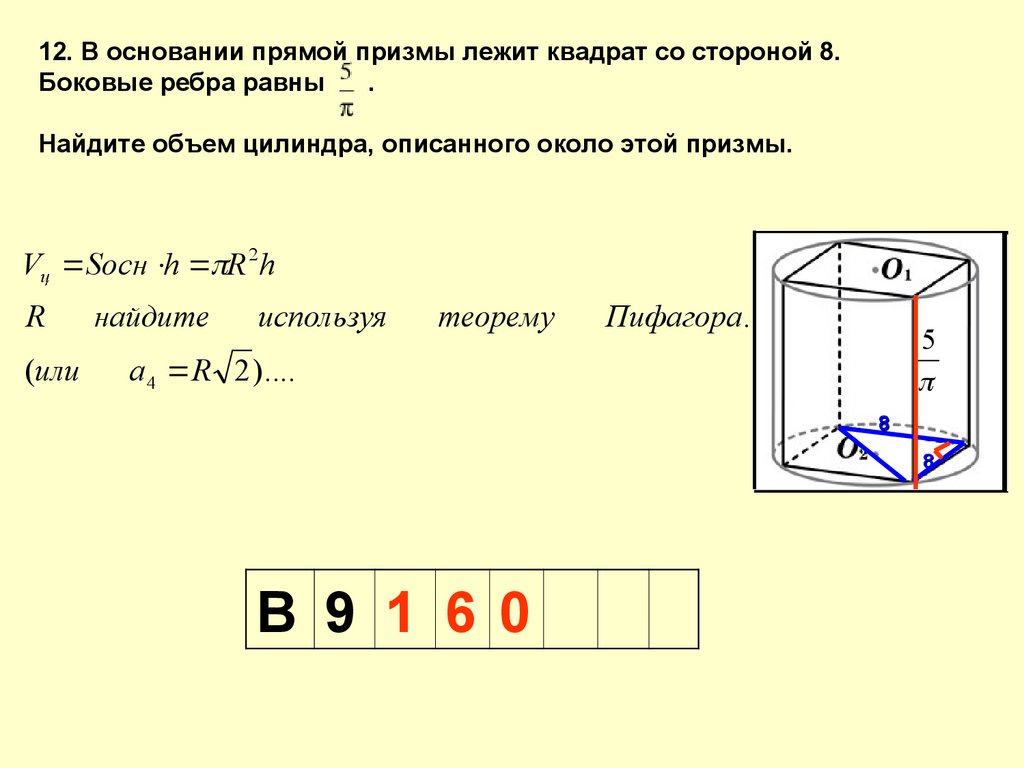
12. В основании прямой призмы лежит квадрат со стороной 8.Боковые ребра равны
.
Найдите объем цилиндра, описанного около этой призмы.
Vц Sосн h R 2 h
R
(или
найдите
используя
теорему
Пифагора.
5
а4 R 2 )....
8
8
В 9 1 60


 Математика
Математика








