Вероятность равновозможных событий

1.

Сенина Г.Н., Сенин В.Г., МБОУ «СОШ №4», г. Корсаков
Вероятность равновозможных событий
Домашнее задание
У: с.292-294 – читать; ВИЗ(1-2); № 871(1); 872(а); 874.
Метапредмет – Хаос и порядок

2.

Цель нашего урока
• понятие вероятности;
• статистический подход к понятию
вероятности;
• как вычисляют вероятность
события в том случае, когда все
его исходы равновероятны;
Вероятность случайного
события приближённо равна
частоте наступления
интересующего нас события
при проведении большого
числа экспериментов.
Однако это даст только
приближённое значение
вероятности. Чтобы вычислить
вероятность выпадания орла,
английский математик Карл
Пирсон провёл 24 000
экспериментов по бросанию
монеты. Но, например, для
экспериментального
вычисления возможности
выигрыша в лотерею нам
просто не хватит денег.
целеполагание

3.

Что сделано дома
УЧЕБНИК
№ 858
?
а) 30; б) 24.
УЧЕБНИК
№ 859
?
945,9; 931,9.
УЧЕБНИК
№ 861
?
в) 711;
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

4.

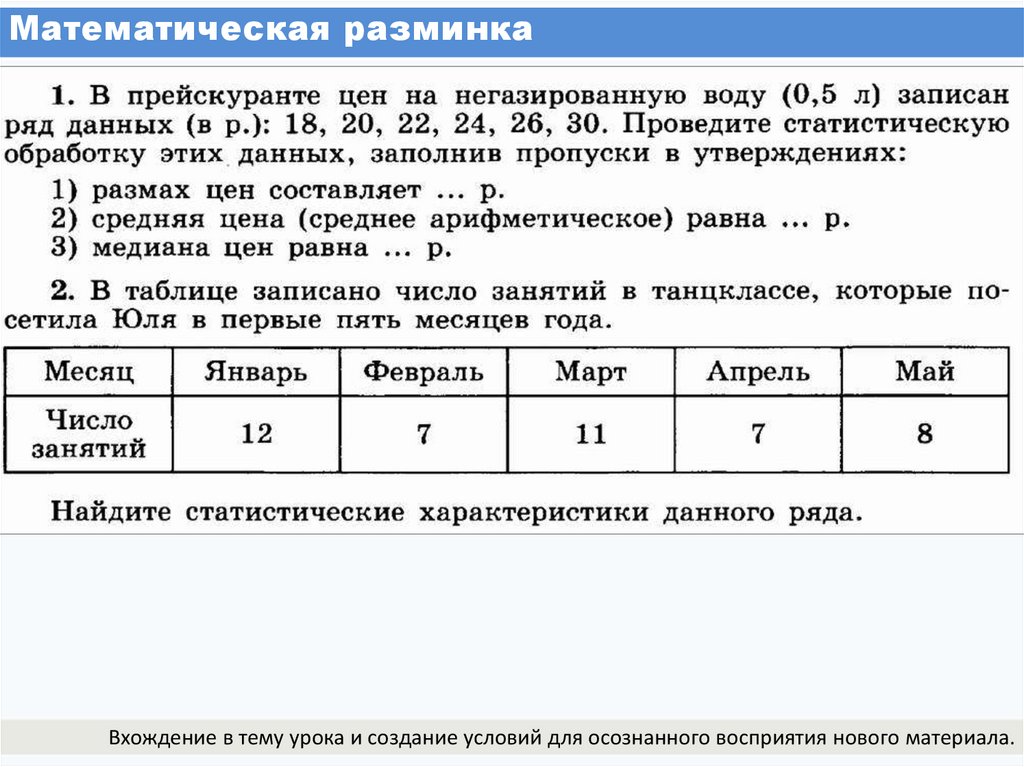
Математическая разминка
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

5.

Вероятность равновозможных событий
Стр.292
Работа с учебником
Если все исходы случайного эксперимента равновозможны, то
вероятность каждого такого исхода можно подсчитать, не проводя
экспериментов.
Проведи анализ примеров 1 – 3.
Если обозначить вероятность наступления события А символом Р(А),
то можно записать формулу
Определение
Для экспериментов с равновероятными исходами вероятностью
случайного события называют отношение числа исходов,
благоприятных для этого события, к числу всех возможных исходов
эксперимента.
Организация и самоорганизация учащихся. Организация обратной связи

6.

Отрабатываем алгоритм
РАБ. ТЕТРАДЬ
Практикум

7.

Отрабатываем алгоритм
РАБ. ТЕТРАДЬ
Практикум

8.

Отрабатываем алгоритм
РАБ. ТЕТРАДЬ
Практикум

9.

Вероятность равновозможных событий
УЧЕБНИК
Верно
б) 0,375; в) 0,95.
?
?
Практикум

10.

Вероятность равновозможных событий
УЧЕБНИК
Р(А) = 1/36; Р(В) = 1/9; Р(С) = 1/2; Р(D) = 8/9;
?
Практикум

11.

Рассуждаем
УЧЕБНИК
ПРОДВИНУТЫМ
Одна красная и пять желтых
Ркр = 4/15; Рж = 0; Рнзел = 1/3; 11 карандашей
?
?
Практикум

12.

Проверь себя
Проверка полученных результатов. Коррекция

13.

Проверь себя
Проверка полученных результатов. Коррекция

14.

Проверь себя
Проверка полученных результатов. Коррекция

15.

Теория вероятности помогает в жизни
Математика — царица всех наук, часто ставится под суд молодыми
людьми.
Выдвигаем тезис «Математика — бесполезна».
И опровергаем на примере одной из самых интересных загадочных и
интересных теорий.
Как теория вероятности помогает в жизни, спасает мир, какие технологии
и достижения основываются на этих, казалось бы, нематериальных и
далеких от жизни формул и сложных вычислений?
Подведение итогов, рефлексия, домашнее задание.