Вероятность равновозможных событий

1. Вероятность равновозможных событий 2 урок

2. Цель:

УЧИТЬСЯ РЕШАТЬ ЗАДАЧИ
НА НАХОЖДЕНИЕ ВЕРОЯТНОСТИ
СЛУЧАЙНОГО СОБЫТИЯ
С ИСПОЛЬЗОВАНИЕМ ФОРМУЛ
КОМБИНАТОРИКИ

3.

Событие - это результат некоторого испытания
(опыта, измерения, наблюдения).
Все события можно разделить на:
невозможные
При данных
условиях произойти
НЕ могут
1. З0 февраля день
рождения.
2. При
подбрасывании
кубика выпадает
7 очков.
3. Человек
рождается старым.
случайные
Происходят
в определенных
условиях,
одни чаще,
другие реже
1.Найти клад.
2. Бутерброд
падает
маслом вниз.
3. В школе
отменили уроки.
4. В доме живет
кошка.
достоверные
Происходят
при каждом
проведении опыта
1. После зимы
наступает весна.
2. После ночи
приходит утро.
3. Камень падает
вниз.
4. Вода становится
теплее
при нагревании.

4.

Для каждого из описанных событий определите, каким
оно является:
невозможным, достоверным или случайным.
1) Из 25 учащихся класса двое справляют день рождения
30 января.
2) Из 25 учащихся класса двое справляют день рождения
30 февраля.
3) Измерены длины сторон треугольника. Оказалось, что
длина каждой стороны меньше суммы длин двух других
сторон.
4) Бросают две игральные кости, сумма выпавших на двух
костях очков меньше 15.
5) Бросают четыре игральные кости, на всех четырех костях
выпало по 3 очка.
6) На уроке математики ученики решали математические
задачи.
7) Из интервала (1; 2) наугад взяли какое-то число, оно
оказалось натуральным.

5.

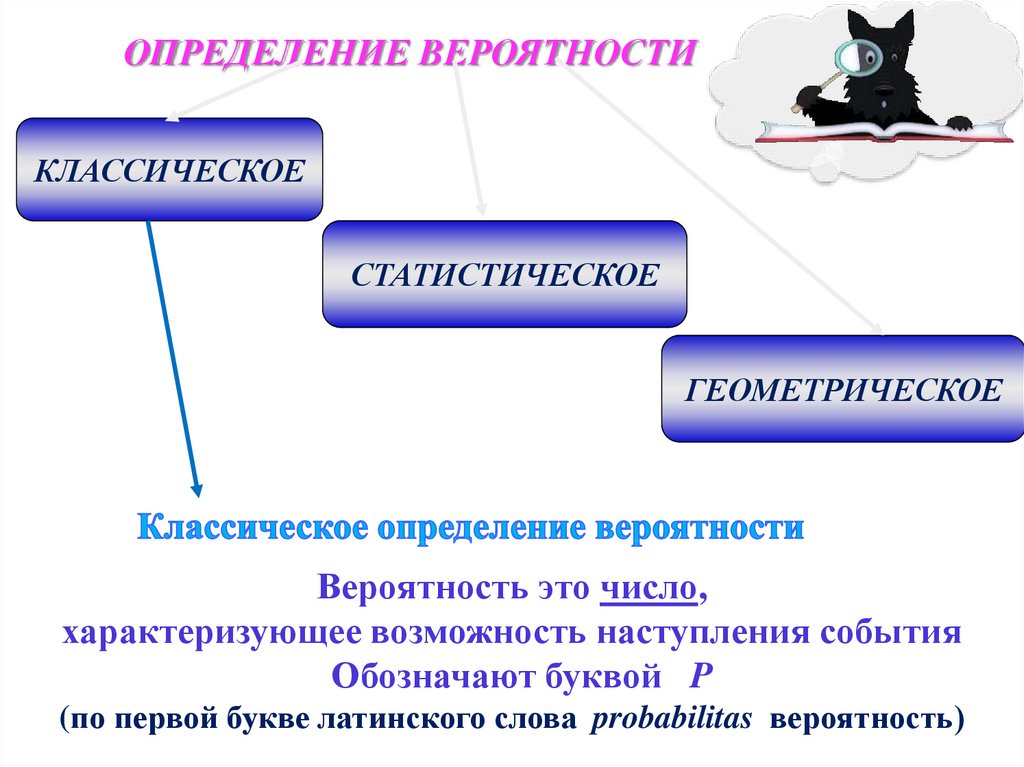
ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
КЛАССИЧЕСКОЕ
СТАТИСТИЧЕСКОЕ
ГЕОМЕТРИЧЕСКОЕ
Вероятность это число,
характеризующее возможность наступления события
Обозначают буквой P
(по первой букве латинского слова probabilitas вероятность)

6.

Формула классической вероятности
где
m – число благоприятных исходов,
n - число всех возможных исходов.
Вероятностью события А называется отношение
числа благоприятных для него исходов испытания
к числу всех равновозможных исходов.
Случай, который приводит к наступлению
события А, называется благоприятным .

7. Вероятностная шкала

Чем больше у случайного события шансов произойти,
тем оно более вероятно и тем правее его следует
расположить на вероятностной шкале;
чем меньше шансов - тем левее.
Если два события, на наш взгляд, имеют равные шансы,
будем располагать их в одном и том же месте шкалы
друг над другом.
События:
Вероятность: 0
Случайные
0,5
0 ≤ Р ≤1
1

8.

Алгоритм решения задачи по формуле
классической вероятности
1. Определить, что является событием А
2. Найти число всех равновозможных исходов n
3. Найти число благоприятных для события А
исходов m
4. Вычислить вероятность Р(А) по формуле:
5. Записать ответ на вопрос задачи,
не забывая, что 0 < Р(А) < 1.

9.

Пример
Папа, мама, сын и дочка бросили жребий –
кому мыть посуду.
Найдите вероятность того, что посуду
будет мыть мама.
Решение
1. Определим событие А - жребий выпал на маму
2. Найдем число всех равновозможных
исходов (папа, мама, сын, дочка) n = 4
3. Найдем число благоприятных исходов m = 1
4. Вычислим вероятность Р(А) по формуле:
Ответ: 0,25

10.

Для подсчета числа исходов в задачах
на вероятность можно использовать приемы
комбинаторики (перебор вариантов, дерево
возможных вариантов, таблицу, граф) и формулы
комбинаторики:
Наименование
Перестановки
из n элементов
Существенные отличия
Формула
Отличаются только порядком
выбранных n элементов
Рn= n!
Сочетания
Отличаются только составом
n!
из п элементов по k входящих в комбинацию k
k
Cn
элементов, без учета порядка их
k! (n k )!
расположения
Размещения
Отличаются как составом, так и
из п элементов по k порядком расположения k
элементов в комбинации
n!
A
(n k )!
k
n

11.

Решение задач из учебника
№ 805
Решение:
1. Событие А – «после набора цифр сейф откроется»
2. Общее число равновозможных исходов –
все возможные перестановки из 5 цифр:
n = Р5 = 5! = 120.
3. Число благоприятных исходов т = 1
(есть только один правильный набор)
т
1
4. Р(А) =
=
.
п
5. О т в е
120
1
т: 120 .

12.

Решение задач из учебника
№ 811
Решение:
1. Событие А – «обе детали оказались стандартными»,
2. Равновозможные исходы – все возможные пары
деталей из 10, находящихся в ящике.
10! 9 · 10
2
С
Общее число исходов n = 10
= 45
2!8! 1 · 2
(порядок деталей в паре не учитывается).
3. Число благоприятных событию А исходов
(из 9 стандартных по 2 детали)
9!
8 ·9
m = С92
= 36 .
2!7!
4. Искомая вероятность: Р(А) =
5. О т в е т: 0,8.
1·2
т
п
36
4
= 0,8.
=
45
5

13.

Решение задач из учебника
1. Оформить решение задач № 798 – 808
на вычисление вероятности по алгоритму.
2. Решить № 809, 810.
3. Решить № 812-813.
4. Решить № 815. Повторить (п.35) геометрическую
вероятность.
На оценку 3-4 выполнить п.1-2.
На оценку 4-5 выполнить п.1, 3, 4