Похожие презентации:
Техническая механика
1. Техническая механика
Курс лекций для студентовдневного, вечернего и
заочного отделений
2.
Рабочая поурочная программапо дисциплине «Техническая механика»
( Теория – 68 часов, практических работ - 12 часов)
Раздел 1. Теоретическая механика
Занятие 1. (2 часа) Основные понятия и аксиомы статики
Занятие 2. (2 часа) Плоская система сходящихся сил. Определение
равнодействующей геометрическим способом
Занятие 3. (2 часа) Плоская система сходящихся сил. Определение
равнодействующей аналитическим способом.
Занятие 4. (2 часа) Пара сил и момент силы относительно точки
Занятие 5. (2 часа) Плоская система произвольно расположенных сил
Занятие 6. (2 часа) Балочные системы. Определение реакций опор и
моментов защемления
Занятие 7. (2 часа) Контрольная работа №1
3.
Предмет: Техническая механика:80 час
Литература:
1. В. П. Олофинская
ТЕХНИЧЕСКАЯ МЕХАНИКА
2. М.С. Мовнин. А.Б. Израелит
А.Г. Рубашкин
ОСНОВЫ ТЕХНИЧЕСКОЙ МЕХАНИКИ
4.
Занятие 8. (2 часа) Пространственная система сил. Центр тяжести.Занятие 9. (2 часа) Основные понятия кинематики
Занятие 10. (2 часа) Кинематика точки.
Занятие 11. (2 часа) Простейшие движения твердого тела.
Занятие 12. (2 часа) Сложное движение точки. Сложное движение
твердого тела.
Занятие 13. (2 часа) Основные понятия и аксиомы динамики.
Понятия о трении.
Занятие 14. (2 часа) Движение материальной точки. Метод
кинетостатики .
Занятие 15. (2 часа) Работа и мощность.
Занятие 16. (2 часа) Коэффициент полезного действия . Общие
теоремы динамики.
Занятие 17. (2 часа) Контрольная работа №2
5.
Раздел 2. Сопротивление материаловЗанятие 18. (2 часа) Основные положения. Допущения, принятые
при расчетах
Занятие 19. (2 часа) Основные положения. Нагрузки внешние и
внутренние. Метод сечений.
Занятие 20. (2 часа) Растяжение и сжатие. Внутренние силовые
факторы. Напряжение.
Занятие 21. (2 часа) Растяжение и сжатие. Продольные и
поперечные деформации. Закон Гука
Занятие 22. (2 часа) Механические испытания, механические
характеристики. Предельные и допускаемые напряжения..
Занятие 23. (2 часа) Кручение. Внутренние силовые факторы.
Построение эпюр крутящих моментов. Расчеты на прочность и
жесткость
Занятие 24. (2 часа) Изгиб. Классификация видов изгиба.
Построение эпюр поперечных сил и изгибающих моментов
Занятие 25. (2 часа) Контрольная работа №3
6.
Раздел 3. Детали машин.Занятие 26. (2 часа) Детали машин и
механизмов;
Занятие 27. (2 часа) Соединения деталей
Занятие 28. (2 часа) Фрикционные передачи.
Зубчатые передачи. Червячные передачи
Занятие 29. (2 часа) Реечные передачи.
Кривошипно – шатунные передачи. Кулисные
механизмы
Занятие 30. (2 часа). Контрольная работа №4
Занятие 32. (2 часа) Зачетное занятие по курсу
Занятие 34. (2 часа) Зачетное занятие по курсу
7.
Практические занятия по разделу«Теоретическая механика»
Практическое занятие 1. (2 часа) Плоская
система сходящихся сил
Практическое занятие 2. (2 часа) Плоская
система произвольно расположенных сил
Практическое занятие 3. (2 часа) Центр
тяжести
Практическое занятие 4. (2 часа) Кинематика
точки. Простейшие движения твердого тела
Практическое занятие 5. (2 часа) Работа и
мощность. Общие теоремы динамики
Зачет по практическим занятиям (2 часа)
8. Раздел 1. Теоретическая механика Занятие 1. Основные понятия и аксиомы статики
9.
1.1. Задачи теоретической механикиТеоретическая механика — наука о
механическом движении
материальных твердых тел и их
взаимодействии.
Механическое движение понимается
как перемещение тела в
пространстве и во времени по
отношению к другим телам, в
частности к Земле.
10.
1.2. Понятие о силе и системе силСила — это мера механического
взаимодействия материальных тел между
собой. Взаимодействие характеризуется
величиной и направлением, т.е. сила есть
величина векторная, характеризующаяся
точкой приложения (А), направлением
(линией действия), величиной (модулем)
(рис. 1.1).
Силу измеряют в ньютонах,
1Н= 1кг • м/с2.
11.
Рис.1.1. Точка приложения , линия действия, модуль силы12.
Силы, действующие на тело (или системутел), делятся на внешние и внутренние.
Внешние силы бывают активные и
реактивные.
Активные силы вызывают перемещение
тела, реактивные стремятся
противодействовать перемещению тела
под действием внешних сил.
Внутренние силы возникают в теле под
действием внешних сил.
13.
Совокупность сил, действующих на какоелибо тело, называют системой сил.Эквивалентная система сил — система
сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю)
системой сил называется такая
система, которая, будучи приложенной
к телу, не изменяет его состояния.
Систему сил, действующих на тело,
можно заменить одной
равнодействующей, действующей так,
как система сил.
14.
Система сил15.
Уравновешенная система сил16.
Равнодействующая системы сил17. 1.3. Аксиомы статики
В результате обобщения человеческогоопыта были установлены общие
закономерности механического
движения, выраженные в виде законов
и теорем.
Все теоремы и уравнения статики
выводятся из нескольких исходных
положений. Эти положения называют
аксиомами статики.
18.
1.3.1. Первая аксиомаПод действием уравновешенной системы
сил абсолютно твердое тело или
материальная точка находятся в
равновесии или движутся равномерно и
прямолинейно (закон инерции).
19.
1.3.2. Вторая аксиомаДве силы, равные по модулю и
направленные по одной прямой в
разные стороны, уравновешиваются
(рис. 1.2).
Рис.1.2. Вторая аксиома статики
20.
1.3.3. Третья аксиомаНе нарушая механического состояния
тела, можно добавить или убрать
уравновешенную систему сил (принцип
отбрасывания системы сил,
эквивалентной нулю) (рис. 1.3).
Рис.1.3. Третья аксиома статики
21.
1.3.4. Четвертая аксиома (правилопараллелограмма сил)
Равнодействующая двух сил, приложенных в
одной точке, приложена в той же точке и
является диагональю параллелограмма,
построенного на этих силах как на сторонах
Рис.1.4. Четвертая аксиома (правило параллелограмма сил)
22.
Вместо параллелограмма можно построитьтреугольник или многоугольник сил: силы
вычерчивают одну за другой в любом
порядке; равнодействующая двух сил
соединяет начало первой силы с концом
последней.
23.
1.3.5. Пятая аксиомаПри взаимодействии тел всякому действию
соответствует равное и противоположно
направленное противодействие (рис. 1.5).
Рис.1.5. Пятая аксиома статики
24.
Силы действующие и противодействующиевсегда приложены к разным телам, поэтому
они не уравновешиваются.
Силы, с которыми два тела действуют друг на
друга, всегда равны по модулю и направлены
вдоль одной прямой в разные стороны.
25.
Следствие из второй и третьейаксиом
Силу, действующую на твердое тело»
можно перемешать вдоль линии ее
Рис.1.6. Следствие из второй и третьей аксиом
26.
Сила F приложена в точке А. Требуетсяперенести ее в точку В.
Используя третью аксиому, добавим в точке В
уравновешенную систему сил (F’, F”).
Образуется уравновешенная по второй
аксиоме система сил [F; F"), Убираем ее и
получим в точке В силу F" равную заданной F.
27.
1.4. Связи и реакции связейВсе законы и теоремы статики
справедливы для свободного твердого
тела.
Все тела делятся на свободные и
связанные.
Свободные тела — тела, перемещение
которых не ограничено.
Связанные тела — тела, перемещение
которых ограничено другими телами.
28.
Teла, ограничивающие перемещение другихтел - называют связями.
Силы, действующие от связей и
препятствующие перемещению, называют
реакциями связей
Реакция связи всегда направлена с той
стороны, куда нельзя перемещаться.
Всякое связанное тело можно
представить свободным, если связи
заменить их реакциями (принцип
освобождения от связей).
Все связи можно разделить на несколько типов.
29.
а. Связь – гладкая опора.Рис.1.7. Связь – гладкая опора.
Реакция опоры приложена в точке опоры и всегда
направлена перпендикулярно опоре (рис. 1.7).
30.
б. Гибкая связь (нить, веревка, трос, цепь)Груз подвешен на двух нитях (рис. 1.8).
Реакция нити направлена вдоль нити от тела,
при этом нить может быть только растянута.
Рис.1.8. Гибкая связь
31.
в. Жесткий стерженьНа схемах стержни изображают толстой сплошной
линией (рис. 1.9).
Рис.1.9. Связь – жесткий стержень
Стержень может быть сжат или растянут. Реакция
стержня направлена вдоль стержня. Стержень
работает на растяжение или сжатие. Точное
направление реакции определяют, мысленно убрав
стержень и рассмотрев возможные перемещения тела
без этой связи.
32.
Возможным перемещением точкиназывается такое бесконечно
малое мысленное перемещение,
которое допускается в данный
момент наложенными на него
связями.
Убираем стержень 1, в этом случае
стержень 2 падает вниз.
Следовательно, сила от стержня 1
(реакция) направлена вверх.
Убираем стержень 2.
В этом случае точка А опускается
вниз, отодвигаясь от стены.
Следовательно, реакция стержня
2 направлена к стене
33.
г. Шарнирная опораШарнир допускает поворот вокруг точки
закрепления. Различают два вида шарниров.
1. Подвижный шарнир.
Рис.1.10. Подвижный шарнир.
34.
Стержень, закрепленный нашарнире, может
поворачиваться вокруг
шарнира, а точка крепления
может перемещаться вдоль
направляющей (площадки)
(рис. 1.10).
Реакция подвижного шарнира
направлена перпендикулярно
опорной поверхности, т.к. не
допускается только
перемещение поперек опорной
поверхности
35.
2. Неподвижный шарнирТочка крепления
перемещаться не может.
Стержень может свободно
поворачиваться вокруг оси
шарнира. Реакция такой
опоры проходит через ось
шарнира, но неизвестна по
направлению. Ее принято
изображать в виде двух
составляющих:
Рис.1.11. Неподвижный шарнир
горизонтальной и
вертикальной (Rx, Ry) (рис.
1.11).
36.
д. Защемление или«заделка»
Любые перемещения
точки крепления
невозможны.
Под действием внешних
сил в опоре возникают
реактивная сила и
реактивный момент MR,
препятствующий повороту
(рис. 1.12).
Рис.1.12. Защемление или «заделка»
37.
Реактивную силу принято представлять в видедвух составляющих вдоль осей координат
R = Rx + Ry
Рис.1.12. Защемление или «заделка»
38.
Примеры решения задачПример 1. Груз подвешен на стержнях и
канатах и находится в равновесии (рис. 1.13).
Изобразить систему сил, действующих на
шарнир А.
39.
Решение1. Реакции стержней направлены вдоль
стержней, реакции гибких связей направлены
вдоль нитей в сторону натяжения (рис. 1.13
а).
2. Для определения точного направления
усилий в стержнях мысленно убираем
последовательно стержни 1 и 2. Анализируем
возможные перемещения точки А.
Неподвижный блок с действующими на него
силами не рассматриваем.
40.
3. Убираем стержень 1, точкаА поднимается и отходит от
стены, следовательно,
реакция стержня 1
направлена к стене.
4. Убираем стержень 2, точка
А поднимается и
приближается к стене,
следовательно, реакция
стержня 2 направлена от
стены вниз.
5. Канат тянет вправо.
6. Освобождаемся от связей
(рис. 1.13 б).
41.
Пример 2. Шар подвешен на нити и опираетсяна стену (рис. 1.14а). Определить реакции
нити и гладкой опоры (стенки).
Решение
1. Реакция нити — вдоль нити к точке В вверх
(рис. 1.14 б).
2. Реакция гладкой опоры (стенки) — по
нормали от поверхности опоры.
42. Занятие 2. (2 часа) Плоская система сходящихся сил. Определение равнодействующей геометрическим способом
43.
2.1. Плоская системасходящихся сил
Система сил, линии действия
которых пересекаются в одной
точке, называется сходящейся
(рис. 2.1).
Необходимо определить
равнодействующую системы
сходящихся сил (F1; F2; F3;
….Fn), n — число сил, входящих
в систему.
По следствию из аксиом
статики, все силы системы
можно переместить вдоль линии
действия, и все силы окажутся
приложенными в одной точке.
Рис.2.1. Плоская система
сходящихся сил
44.
2.2. Равнодействующая сходящихся силРавнодействующую двух пересекающихся сил
можно определить с помощью
параллелограмма или треугольника сил
(4-я аксиома) (рис. 2.2).
Рис.2.2. Равнодействующая сходящихся сил
45.
Используя свойства векторной суммы сил, можнополучить равнодействующую любой сходящейся
системы сил, складывая последовательно силы,
входящие в систему. Образуется многоугольник сил
(рис. 2.3). Вектор равнодействующей силы соединит
начало первого вектора с концом последнего.
Рис.2.3. Определение равнодействующей с помощью многоугольника сил
46.
При графическом способе определенияравнодействующей векторы сил можно
вычерчивать в любом порядке, результат
(величина и направление
равнодействующей) при этом не изменится.
Вектор равнодействующей направлен
навстречу векторам сил слагаемых. Такой
способ получения равнодействующей
называют геометрическим.
Замечание. При вычерчивании многоугольника
обращать внимание на параллельность
сторон многоугольника соответствующим
векторам сил.
47.
Порядок построения многоугольника сил1. Вычертить векторы сил заданной системы в
некотором масштабе один за другим так,
чтобы конец предыдущего вектора совпадал
с началом последующего.
2. Вектор равнодействующей замыкает
полученную ломаную линию; он соединяет
начало первого вектора с концом последнего
и направлен ему навстречу.
3. При изменении порядка вычерчивания
векторов в многоугольнике меняется вид
фигуры. На результат порядок
вычерчивания не влияет.
48.
2.3. Условие равновесия плоской системысходящихся сил
При равновесии системы сил
равнодействующая должна быть равна нулю,
следовательно, при геометрическом
построении конец последнего вектора
должен совпасть с началом первого.
Если плоская система сходящихся сил
находится в равновесии, многоугольник
сил этой системы должен быть
замкнут.
49.
Если в системе три силы, образуетсятреугольник сил.
Сравните два треугольника сил (рис. 2.4) и
сделайте вывод о количестве сил, входящих
в каждую систему.
Рекомендация. Обратить внимание на
направление векторов.
Рис.2.4. Условие равновесия плоской системы сходящихся сил
50.
2.4. Решение задач на равновесие геометрическимспособом
Порядок решения задач:
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с
известных сил в некотором масштабе.
(Многоугольник должен быть замкнут, все векторыслагаемые направлены в одну сторону по обходу
контура.)
3. Измерить полученные векторы сил и определить их
величину, учитывая выбранный масштаб.
4. Для уточнения решения рекомендуется определить
величины векторов (сторон многоугольника) с
помощью геометрических зависимостей.
51.
Пример 1. Груз подвешен на стержнях инаходится в равновесии. Определить усилия
в стержнях (рис. 2.5а).
52.
РешениеУсилия, возникающие в
стержнях крепления, по
величине равны силам, с
которыми стержни
поддерживают груз (5-я
аксиома статики) (рис. 2.5а).
Определяем возможные
направления реакций связей
«жесткие стержни».
Усилия направлены вдоль
стержней.
2. Освободим точку А от
связей, заменив действие
связей их реакциями
(рис. 2.5 б).
53.
3. Система находится вравновесии. Построим
треугольник сил. Построение
начнем с известной силы,
вычертив вектор F в некотором
масштабе.
Из концов вектора F проводим
линии, параллельные реакциям
R1 и R2.
Пересекаясь, линии создадут
треугольник (рис. 2.5в). Зная
масштаб построений и измерив
длину сторон треугольника,
можно определить величину
реакций в стержнях.
54.
4. Для более точных расчетов можно воспользоватьсягеометрическими соотношениями, в частности
теоремой синусов: отношение стороны треугольника
к синусу противоположного угла — величина
постоянная
Для данного случая:
55.
Замечание. Если направление вектора(реакции связи) на заданной схеме и в
треугольнике сил не совпало, значит, реакция
на схеме должна быть направлена в
противоположную сторону.
56.
Пример 2. Груз подвешен на стержнях иканатах и находится в равновесии.
Определить усилия в стержнях (рис. 2.6а).
57.
1. Нанесем на схему возможныенаправления усилий, приложенных в
точке А. Реакции стержней — вдоль
стержней, усилие от каната — вдоль
каната от точки А к точке В.
2. Груз находится в равновесии,
следовательно, в равновесии
находится точка А, в которой
пересекаются три силы.
Освободим точку А от связей и
рассмотрим ее равновесие (рис. 2.6б).
Замечание. Рассмотрим только силы,
приложенные к точке А. Груз
растягивает канат силой 45 кН по всей
длине, поэтому усилие от каната
известно: Тз = 45 кН.
58.
3. Строим треугольникдля сил, приложенных в
точке А, начиная с
известной силы Тз.
Стороны треугольника
параллельны
предполагаемым
направлениям сил,
приложенных в точке А.
Образовался
прямоугольный
треугольник (рис 2.6в).
59.
4. Неизвестные реакции стержней можно определить изсоотношений в прямоугольном треугольнике:
Замечание. При равновесии векторы сил в
треугольнике направлены один за другим (обходим
треугольник по часовой стрелке). Сравним
направления сил в треугольнике с принятыми в
начале расчета на рис. 1.26а. Направления совпали,
следовательно, направления реакций определены
верно.
60. Занятие 3. (2 часа) Плоская система сходящихся сил. Определение равнодействующей аналитическим способом.
61.
3.1. Проекция силы на осьПроекция силы на ось определяется отрезком оси,
отсекаемым перпендикулярами, опущенными на ось
из начала и конца вектора (рис. 3.1).
Рис.3.1. Проекция силы на ось.
Величина проекции силы на ось равна произведению
модуля силы на косинус угла между вектором силы и
положительным направлением оси.
62.
Таким образом, проекция имеет знак: положительныйпри одинаковом направлении вектора силы и оси и
отрицательный при направлении в сторону
отрицательной полуоси (рис. 3.2).
Рис.3.2. Знак проекции
63.
Проекция силы на две взаимноперпендикулярные оси.
Рис.3.3. Проекция силы на две взаимно перпендикулярные оси.
64.
3.2. Определение равнодействующей системысил аналитическим способом
Величина равнодействующей равна векторной
(геометрической) сумме векторов системы сил.
Определяем равнодействующую геометрическим
способом. Выберем систему координат, определим
проекции всех заданных векторов на эти оси
(рис. 3.4а). Складываем проекции всех векторов на
оси х и у (рис. 3.4 б).
Рис.3.4. Определение равнодействующей системы сил аналитическим способом
65.
Модуль (величину) равнодействующей можно найти поизвестным проекциям:
66.
Направление вектора равнодействующей можноопределить по величинам и знакам косинусов углов,
образуемых равнодействующей с осями координат
(рис. 3.5).
Рис.3.5. Определение направления вектора
равнодействующей
67.
68.
3.3. Условия равновесия плоской системысходящихся сил в аналитической форме
Исходя из того, что равнодействующая равна нулю,
получим:
Условия равновесия в аналитической форме можно
сформулировать следующим образом:
Плоская система сходящихся сил находится в
равновесии, если алгебраическая сумма проекций всех
сил системы на любую ось равна нулю.
69.
Система уравнений равновесия плоской сходящейсясистемы сил:
В задачах координатные оси выбирают так, чтобы
решение было наиболее простым. Желательно,
чтобы хотя бы одна неизвестная сила совпадала с
осью координат
70.
71.
72.
73.
74.
75.
76. Занятие 4. (2 часа) Пара сил и момент силы относительно точки
77.
4.1. Пара сил. Момент пары сил.Парой сил называется система двух
сил, равных по модулю,
параллельных и направленных в
разные стороны.
Рассмотрим систему сил (F;F’),
образующих пару.
Пара сил вызывает вращение тела и
ее действие на тело оценивается
моментом. Силы, входящие в пару,
не уравновешиваются, т. к. они
приложены к двум точкам (рис. 4.1).
Их действие на тело не может быть
заменено одной силой
(равнодействующей).
78.
Момент пары сил численноравен произведению модуля
силы на расстояние между
линиями действия сил (плечо
пары).
Момент считают
положительным, если пара
вращает тело по часовой
стрелке (рис. 4.1б): M(F;F') =
Fa;
М > 0.
Плоскость, проходящая через
линии действия сил пары,
называется плоскостью
действия пары.
79.
4.2. Свойства пар (без доказательств):1. Пару сил можно перемещать в плоскости ее действия.
2. Эквивалентность пар. Две пары, моменты которых равны,
(рис. 4.2) эквивалентны (действие их на тело аналогично).
3. Сложение пар сил. Систему пар сил можно заменить
равнодействующей парой.
Момент равнодействующей пары равен алгебраической сумме
моментов пар, составляющих систему (рис. 4.3):
80.
4. Равновесие пар.Для равновесия пар необходимо и достаточно,
чтобы алгебраическая сумма моментов пар
системы равнялась нулю:
81.
4.3. Момент силы относительно точкиСила, не проходящая через точку крепления тела, вызывает
вращение тела относительно точки, поэтому действие такой
силы на тело оценивается моментом.
Момент силы относительно точки численно равен произведению
модуля силы на расстояние от точки до линий действия силы.
Перпендикуляр, опущенный из точки на линию действия силы
(рис. 4.4), называется плечом силы.
Рис.4.4. Момент силы относительно точки
82.
Обозначение момента МО(F);или mО(F);mО(F) = Fα.
Единица измерения [mО(F)] = Н∙м.
Момент считается положительным, если сила
разворачивает тело по часовой стрелке.
Примечание. В разных учебных пособиях знак
момента назначается по-разному.
Момент силы относительно точки равен нулю,
если линия действия силы проходит через
точку, т.к. в этом случае расстояние от точки
до силы равно нулю
83.
84.
Примечание. Чтобы уравновесить данную систему пар, необходимоприложить пару сил, равную по модулю и направленную в обратную
сторону. Такую пару сил называют уравновешивающей.
85.
86. Занятие 5. (2 часа) Плоская система произвольно расположенных сил
87.
5.1. Теорема Пуансо о параллельном переносе сил.Силу можно перенести параллельно линии ее действия, при этом
нужно добавить пару сил с моментом, равным произведению
модуля силы на расстояние, на которое перенесена сила.
Рис.5.1. Теорема Пуансо о параллельном переносе сил.
Дано: сила в точке А (рис. 5.1).
Добавим в точке Б уравновешенную систему сил (F'\F").
Образуется пара сил (F; F’). Получим силу в точке В и момент
пары т
88.
5.2. Приведение к точке плоской системыпроизвольно расположенных сил
Линии действия произвольной системы сил не
пересекаются в одной точке, поэтому для оценки
состояния тела такую систему следует упростить.
Для этого все силы системы переносят в одну
произвольно выбранную точку — точку приведения.
Применяют теорему Пуансо. При любом переносе силы
в точку, не лежащую на линии ее действия,
добавляют пару сил.
Появившиеся при переносе пары называют
присоединенными парами.
89.
Дана плоская система произвольно расположенных сил (рис. 5.2).Рис.5.2. Приведение к точке плоской системы произвольно расположенных сил
Переносим все силы в точку О. Получим пучок сил в точке О,
который можно заменить одной силой — главным вектором
системы.
90.
Образующуюся систему пар сил можно заменить однойэквивалентной парой — главным моментом системы.
91.
Главный вектор равен геометрической сумме векторовпроизвольной плоской системы сил. Проецируем все силы
системы на оси координат и, сложив соответствующие проекции
на оси, получим проекции главного вектора.
По величине проекций главного вектора на оси координат находим
модуль главного вектора:
92.
Главный момент системы сил равен алгебраическойсумме моментов сил системы относительно точки
приведения.
Таким образом, произвольная плоская система сил
приводится к одной силе (главному вектору системы
сил) и одному моменту (главному моменту системы
сил).
93.
5.3. Влияние точки приведенияТочка приведения выбрана произвольно. При
изменении положения точки приведения величина
главного вектора не изменится.
Величина главного момента при переносе точки
приведения изменится, т. к. меняются расстояния от
векторов сил до новой точки приведения.
С помощью теоремы Вариньона о моменте
равнодействующей можно определить точку на
плоскости, относительно которой главный момент
равен нулю. Тогда произвольная плоская система
сил может быть заменена одной силой.
Эту силу называют равнодействующей системы сил.
94.
Численно равнодействующая равна главномувектору системы сил, но приложена в другой
точке, относительно которой главный момент
равен нулю. Равнодействующую принято
обозначать FΣ
Численно ее значение определяется так же, как
главный вектор системы сил:
95.
Точку приложения равнодействующей можноопределить по формуле
где d — расстояние от выбранной точки
приведения до точки приложения
равнодействующей;
Мгл — величина главного момента
относительно выбранной точки приведения;
Fгл — величина главного вектора системы сил.
96.
5.4. Частные случаи приведения системы сил к точкеПри приведении системы сил к точке возможны
следующие варианты:
→ тело вращается вокруг неподвижной оси.
→ тело движется прямолинейно ускоренно.
→ тело находится в равновесии.
97.
5.4. Условие равновесия произвольной плоскойсистемы сил
1. При равновесии главный вектор системы равен нулю
(Fгл = 0).
где
Fkx и Fky — проекции векторов на оси координат.
98.
2. Поскольку точка приведения выбрана произвольно, ясно, чтопри равновесии сумма моментов сил системы относительно
любой точки на плоскости должна равняться нулю:
где: А и В — разные точки приведения.
Условие равновесия произвольной плоской системы сил может
быть сформулировано следующим образом:
Для того чтобы твердое тело под действием произвольной плоской
системы сил находилось в равновесии, необходимо и
достаточно, чтобы алгебраическая сумма проекций всех сил
системы на любую ось равнялась нулю и алгебраическая сумма
моментов всех сил системы относительно любой точки в
плоскости действия сил равнялась нулю.
99.
Получим основную форму уравнения равновесия:Теоретически уравнений моментов можно записать бесконечное
множество, но практически доказано, что на плоскости можно
составить только три независимых уравнения моментов и при
этом три точки (центры моментов) не должны лежать на одной
линии.
Таким образом, имеем пять независимых уравнений равновесия.
Практически для решения задач на плоскости достаточно трех
уравнений равновесия. В каждом конкретном случае
используются уравнения с одним неизвестным.
100.
Для разных случаев используются три группы уравненийравновесия.
101.
Для частного случая, если уравновешенасистема параллельных сил, можно составить
только два уравнения равновесия:
Ось Ох системы координат параллельна линии
действия сил.
102.
103.
104.
105.
106. Занятие 6. (2 часа) Балочные системы. Определение реакций опор и моментов защемления
107.
6.1. Виды нагрузок и разновидности опор6.1.1. Виды нагрузок
По способу приложения нагрузки делятся на
сосредоточенные и распределенные.
Если реально передача нагрузки происходит на
пренебрежимо малой площадке (в точке), нагрузку
называют сосредоточенной.
Часто нагрузка распределена по значительной
площадке или линии (давление воды на плотину,
давление снега на крышу и т.п.), тогда нагрузку
считают распределенной.
В задачах статики для абсолютно твердых тел
распределенную нагрузку можно заменить
равнодействующей сосредоточенной силой
(рис. 6.1).
108.
Рис.6.1. Замена распределенной нагрузки равнодействующейсосредоточенной силой
q — интенсивность нагрузки;
l — длина стержня;
G = ql — равнодействующая распределенной нагрузки.
109.
6.1.2. Разновидности опор балочных систем (см.занятие 1)Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с длиной.
а) Жесткая заделка (защемление) (рис. 6.2)
Рис.6.2. Жесткая заделка (защемление)
Опора не допускает перемещений и поворотов. Заделку заменяют
двумя составляющими силы RАx и RAy и парой с моментом МR.
110.
Для определения этих неизвестных удобно использовать системууравнений в виде
Каждое уравнение имеет одну неизвестную величину и решается
без подстановок.
Для контроля правильности решений используют дополнительное
уравнение моментов относительно любой точки на балке,
например В:
111.
б) Шарнирно-подвижная опора (рис. 6.3)Опора допускает поворот вокруг шарнира и
перемещение вдоль опорной поверхности. Реакция
направлена перпендикулярно опорной поверхности.
Рис.6.4. Шарнирно-подвижная опора
112.
в) Шарнирно-неподвижная опора (рис. 6.4)Опора допускает поворот вокруг шарнира и может быть
заменена двумя составляющими силы вдоль осей
координат.
Рис.6.4. Шарнирно-неподвижная опора
113.
г) Балка на двух шарнирных опорах (рис. 6.5)Рис.6.5. Балка на двух шарнирных опорах
Не известны три силы, две из них — вертикальные,
следовательно, удобнее для определения неизвестных
использовать систему уравнений во второй форме:
Составляются уравнения моментов относительно точек крепления
балки.
114.
Поскольку момент силы, проходящей через точку крепления, равен0, в уравнении останется одна неизвестная сила.
Для контроля правильности решения используется
дополнительное уравнение:
115.
При равновесии твердого тела, где можно выбрать три точки, нележащие на одной прямой, удобно использовать систему
уравнений в третьей форме (рис. 6.6):
116.
6.2. Примеры решения задачПример 1. Одноопорная (защемленная) балка нагружена
сосредоточенными силами и парой сил (рис. 6.7). Определить
реакции заделки.
Решение:
1. В заделке может возникнуть реакция, представляемая двумя
составляющими (RАу, RАx), и реактивный момент МА. Наносим
на схему балки возможные направления реакций.
117.
Замечание.Если направления выбраны неверно, при расчетах
получим отрицательные значения реакций. В этом
случае реакции на схеме следует направить в
противоположную сторону, не повторяя расчета.
В силу малой высоты считают, что все точки балки
находятся на одной прямой; все три неизвестные
реакции приложены в одной точке.
Для решения удобно использовать систему уравнений
равновесия в первой форме.
Каждое уравнение будет содержать одну неизвестную.
118.
Знаки полученных реакций (+), следовательно, направленияреакций выбраны верно.
119.
3. Для проверки правильности решения составляем уравнениемоментов относительно точки В.
120.
Пример 2. Двухопорная балка с шарнирными опорами А и Внагружена сосредоточенной силой F, распределенной нагрузкой
с интенсивностью q и парой сил с моментом т (рис. 6.8а).
Определить реакции опор.
121.
Решение:1. Левая опора (точка А) — подвижный шарнир, здесь реакция
направлена перпендикулярно опорной поверхности.
Правая опора (точка В) — неподвижный шарнир, здесь наносим
две составляющие реакции вдоль осей координат. Ось Ох
совмещаем с продольной осью балки.
2. Поскольку на схеме возникнут две неизвестные вертикальные
реакции, использовать первую форму уравнений равновесия
нецелесообразно.
3. Заменяем распределенную нагрузку сосредоточенной:
122.
Сосредоточенную силу помещаем в середине пролета, далеезадача решается с сосредоточенными силами (рис. 6.8 б).
4. Наносим возможные
реакции в опорах
(направление
произвольное).
5. Для решения выбираем
уравнение равновесия в
виде
123.
124.
125. Занятие 7. (2 часа) Контрольная работа №1
126. Занятие 8. (2 часа) Пространственная система сил. Центр тяжести.
127.
8.1. Момент силы относительно оси.Момент силы относительно оси равен моменту проекции силы на
плоскость, перпендикулярную оси, относительно точки
пересечения оси с плоскостью (рис. 8.1а).
Moo(F) = пр Fα,
α — расстояние от оси до проекции F;
npF — проекция силы на плоскость, перпендикулярную оси ОО.
npF = F cos α; MОО(F) = F cos α ∙ α.
Рис.8.1. Момент силы относительно оси.
128.
Момент считаем положительным, если силаразворачивает тело по часовой стрелке. Смотреть со
стороны положительного направления оси.
Если линия действия силы пересекает ось или линия
действия силы параллельна оси, моменты силы
относительно этой оси равны нулю (рис. 8.1б).
Силы и ось лежат в одной плоскости, они не смогут
повернуть тело вокруг этой оси.
F1 пересекает ось; MОО(F1) = 0;
F2||ОО- npF2 = 0; MOO(F2) = 0.
129.
8.2. Пространственная сходящаяся система сил.а) вектор в пространстве.
В пространстве вектор силы проецируется на три взаимно
перпендикулярные оси координат. Проекции вектора образуют
ребра прямоугольного параллелепипеда, вектор силы
совпадает с диагональю (рис. 8.2).
Рис.8.2. Вектор в пространстве.
Модуль вектора может быть
получен из зависимости
αх, αу, αz — углы между вектором осями координат.
130.
б) Пространственная сходящаяся система силПространственная сходящаяся система сил — система
сил, не лежащих в одной плоскости, линии действия
которых пересекаются в одной точке.
Равнодействующую пространственной системы сил можно
определить, построив пространственный многоугольник (рис. 8.3),
Рис.8.3. Пространственная сходящаяся система сил.
FΣ = F1 + F2 + F3 + • • • + Fn.
Доказано, что равнодействующая системы сходящихся сил
приложена в точке пересечения линий действия сил системы.
131.
Совмещаем начало координат с точкой пересечения линийдействия сил системы. Проецируем все силы на оси координат
и суммируем соответствующие проекции
(рис. 8.4).
Рис.8.4. Проекции равнодействующей на оси координат
Получим проекции равнодействующей на оси координат:
132.
133.
в) Произвольная пространственная система силПриведение произвольной пространственной системы сил к
центру О
Дана пространственная система сил (рис. 8.5а). Приведем ее к
центру О.
рис. 8.5а
Силы необходимо параллельно перемещать, при этом образуется
система пар сил. Момент каждой из этих пар равен
произведению модуля силы на расстояние до центра
приведения
134.
Главный вектор принято раскладывать на три составляющие,направленные вдоль осей координат (рис. 8.5в).
135.
Обычно суммарный момент раскладывают на составляющие: тримомента относительно осей координат.
Абсолютное значение главного вектора (рис. 8.56) равно
136.
г) Уравнения равновесия пространственной системы силПри равновесии Fгл = 0; Мгл = 0.
Получаем шесть уравнений равновесия:
Шесть уравнений равновесия пространственной системы сил
соответствуют шести независимым возможным перемещениям
тела в пространстве: трем перемещениям вдоль координатных
осей и трем вращениям вокруг этих осей.
137.
138.
139.
140.
141.
142.
8.3. Сила тяжести.Сила тяжести — равнодействующая сил притяжения к Земле,
она распределена по всему объему тела. Силы притяжения,
приложенные к частицам твердого тела, образуют систему сил,
линии действия которых сходятся в центре Земли (рис. 8.8).
Поскольку радиус Земли значительно больше размеров любого
земного тела, силы притяжения можно считать параллельными.
Рис.8.8. Сила тяжести.
143.
8.4. Точка приложения силы тяжести.Для определения точки приложения силы тяжести
(равнодействующей параллельных сил) используем теорему
Вариньона о моменте равнодействующей:
Момент равнодействующей относительно оси равен
алгебраической сумме моментов сил системы
относительно этой оси.
Изображаем тело, составленное из некоторых частей, в
пространственной системе координат (рис. 8.9).
Рис.8.9. Тело, составленное
из частей, в
пространственной системе
координат
144.
Тело состоит из частей, силы тяжести которых qk приложены вцентрах тяжести (ЦТ) этих частей.
Пусть равнодействующая (сила тяжести всего тела) приложена в
неизвестном пока центре С.
Xc, Yс и Zc — координаты центра тяжести С.
Xk, Yk и Zk — координаты центров тяжести частей тела.
145.
146.
147.
8.4. Центр тяжести однородных плоских тел (плоских фигур)Очень часто приходится определять центр тяжести различных
плоских тел и геометрических плоских фигур сложной формы.
Для плоских тел можно записать:
V = Ah,
где А — площадь фигуры, h — ее высота.
Тогда после подстановки в записанные выше формулы получим:
148.
Оси, проходящие через центр тяжести, называются центральнымиосями. Статический момент относительно центральной оси
равен нулю.
149.
8.5. Определение координат центра тяжести плоских фигурПримечание. Центр тяжести симметричной фигуры находится на
оси симметрии.
Центр тяжести стержня находится на середине высоты.
Положения центров тяжести простых геометрических фигур могут
быть рассчитаны по известным формулам (рис. 8.10) :
а) — круг; б) — квадрат, прямоугольник; в) — треугольник;
г) — полукруг).
Рис.8.10.
Определение
координат центра
тяжести плоских фигур
150.
При решении задач используются следующиеметоды:
1) метод симметрии: центр тяжести
симметричных фигур находится на оси
симметрии;
2) метод разделения: сложные сечения
разделяем на несколько простых частей,
положение центров тяжести которых легко
определить;
3) метод отрицательных площадей: полости
(отверстия) рассматриваются как часть
сечения с отрицательной площадью.
151.
152.
Рис.8.12. Составное сечение из листа и прокатных профилей.153.
154. Занятие 9. (2 часа) Основные понятия кинематики
155.
9.1.Основные кинематические параметрыа) Траектория
Линию, которую очерчивает материальная точка при
движении в пространстве, называют траекторией.
Траектория может быть прямой и кривой, плоской и
пространственной линией.
Уравнение траектории при плоском движении: у = f(x).
б) Пройденный путь
Путь измеряется вдоль траектории в направлении
движения. Обозначение — s, единицы измерения —
метры.
156.
в) Уравнение движения точкиУравнение, определяющее положение движущейся точки в
зависимости от времени, называется уравнением движения.
Положение точки в каждый момент времени можно определить по
расстоянию, пройденному вдоль траектории от некоторой
неподвижной точки,
рассматриваемой как начало отсчета (рис. 9.1).
Такой способ задания движения называется естественным.
157.
Таким образом, уравнение движения можно представить в видеS = f (t).
Положение точки можно также определить, если известны ее
координаты в зависимости от времени
(рис. 9.2). Тогда в случае движения на плоскости должны быть
заданы два уравнения:
В случае пространственного движения добавляется и третья
координата
z = f3(t)
Такой способ задания движения называют координатным.
158.
г) Скорость движенияВекторная величина, характеризующая в данный момент быстроту
и направление движения по траектории, называется
скоростью.
Скорость — вектор, в любой момент направленный по
касательной к траектории в сторону направления движения
(рис. 9.3).
Если точка за равные промежутки времени проходит равные
расстояния, то движение называют равномерным.
Рис.9.3. Скорость движения.
159.
Средняя скорость на пути AS определяется какгде ΔS — пройденный путь за время Δt;
Δt — промежуток времени.
Если точка за равные промежутки времени проходит неравные
"пути, то движение называют неравномерным.
В этом случае скорость — величина переменная и зависит от
времени v = f(t).
При рассмотрении малых промежутков времени (Δt → 0) средняя
скорость становится равной истинной скорости движения в
данный момент. Поэтому скорость в данный момент
определяют как производную по времени:
За единицу скорости принимают 1м/с. Иногда скорость измеряют в
км/ч,
160.
д) Ускорение точкиВекторная величина, характеризующая быстроту изменения
скорости по величине и направлению, называется ускорением
точки.
Скорость точки при перемещении из точки M1 в точку М2 меняется
по величине и направлению. Среднее значение ускорения за
этот промежуток времени (см. рис. 9.4.)
Рис.9.4. Ускорение точки.
161.
При рассмотрениибесконечно малого промежутка
времени среднее ускорение
превратится в ускорение в
данный момент:
Обычно для удобства
рассматривают две взаимно
перпендикулярные
составляющие ускорения:
нормальное и касательное
(рис. 9.5).
Нормальное ускорение αn
характеризует изменение
скорости по направлению и
определяется как
→
где r — радиус кривизны
траектории в данный момент
времени.
162.
Касательное ускорение αtхарактеризует изменение
скорости по величине и
всегда направлено по
касательной к траектории;
при ускорении его
направление совпадает с
направлением скорости, а
при замедлении оно
направлено
противоположно
направлению вектора
скорости.
Формула для определения
касательного ускорения
имеет вид:
163.
Значение полного ускорения определяется как:Рис.9.6. Определение полного ускорения
(см. рис. 9.6).
164.
165.
166.
167. Занятие 10. (2 часа) Кинематика точки.
168.
10.1. Анализ видов и кинетических параметров движенийа) Равномерное движение
Равномерное движение — это движение с постоянной скоростью:
v = const.
Для прямолинейного равномерного движения (рис. 10.1а)
Рис.10.1.
Полное ускорение движения точки равно нулю: а = 0.
169.
При криволинейном равномерном движении (рис. 10.1б)рис. 10.1б
Полное ускорение равно нормальному ускорению:
α = αn
Уравнение (закон) движения точки при равномерном движении
можно получить, проделав ряд несложных операций.
Так как v = const, закон равномерного движения в общем виде
является уравнением прямой:
S = So+vt,
где So — путь, пройденный до начала отсчета.
170.
б)Равнопеременное движениеРавнопеременное движение — это движение с постоянным
касательным ускорением:
at = const.
Для прямолинейного равнопеременного движения
Полное ускорение равно касательному ускорению.
Криволинейное равнопеременное движение (рис. 10.2):
рис. 10.2
171.
значение скорости при равнопеременном движениизакон равнопеременного движения в общем виде,
172.
10.2. Кинематические графикиКинематические графики — это графики изменения пути, скорости
и ускорений в зависимости от времени.
а) Равномерное движение (рис. 10.3)
Рис. 10.3 Кинематический график равномерного движения
173.
б) Равнопеременное движение (рис. 10.4)Рис. 10.4 Кинематические графики равнопеременного движения
а) равноускоренное движение
б) равнозамедленное движение
174.
Примеры решения задачПример 1. По заданному графику скорости найти путь,
пройденный за время движения (рис. 10.6).
175.
176.
Пример 2. Тело, имевшее начальную скорость 36 км/ч, прошло50 м до остановки. Считая движение равнозамедленным,
определить время торможения.
177. Занятие 11. (2 часа) Простейшие движения твердого тела.
178.
11.1. Поступательное движениеПоступательным называют такое движение твердого тела, при
котором всякая прямая линия на теле при движении остается
параллельной своему начальному положению (рис. 11.1, 11.2).
При поступательном движении все точки тела движутся одинаково:
скорости и ускорения в каждый момент одинаковы. Поэтому для
описания движения тела можно рассматривать движение одной
его точки, обычно центра масс.
Поступательное движение может быть прямолинейным и
криволинейным.
Рис.11.1 Поступательное движение
Рис.11.2 Поступательное движение
179.
11.2. Вращательное движениеПри вращательном движении
все точки тела описывают окружности вокруг общей неподвижной
оси.
Неподвижная ось, вокруг которой
вращаются все точки тела
называется осью вращения.
При этом каждая точка движется
по окружности, радиус которой
равен расстоянию точки до оси
вращения. Точки на оси вращения
не перемещаются.
Рис.11.3. Вращательное движение
Для описания вращательного
движения тела вокруг неподвижной
оси можно использовать только
φ — угол поворота тела, [φ]= рад;
угловые параметры (рис. 11.3):
ω — угловая скорость, определяет
изменение угла поворота в единицу
времени, [ω] = рад/с.
180.
Для определения положения тела в любой момент временииспользуется уравнение
φ = f(t).
Следовательно, для определения угловой скорости можно
пользоваться выражением:
Иногда для оценки быстроты вращения используют угловую
частоту вращения n, которая оценивается в оборотах в минуту.
Угловая скорость и частота вращения физически близкие
величины:
Изменение угловой скорости во времени определяется угловым
ускорением ε, [ε] = рад/с2;
181.
11.3. Частные случаи вращательного движенияа) Равномерное вращение (угловая скорость постоянна):
ω - const.
Уравнение (закон) равномерного вращения в данном случае имеет
вид:
где φ0 — угол поворота до начала отсчета.
Кинематические графики для этого вида движения изображены на
рис. 11.4.
Рис.11.4. Кинематические графики равномерного вращения
182.
б) Равнопеременное вращение (угловое ускорениепостоянно):
ε =const
Уравнение (закон) равнопеременного вращения
где ω0 — начальная угловая скорость.
Угловое ускорение при ускоренном движении — величина
положительная; угловая скорость будет все время возрастать.
Угловое ускорение при замедленном, движении — величина
отрицательная; угловая скорость убывает.
Для данного движения кинематические графики представлены на
рис. 11.5.
Рис.11.5. Кинематические графики равноускоренного движения.
183.
в) Скорости и ускорения точек вращающегося тела.Тело вращается вокруг точки О. Определим параметры движения
точки А, расположенной на расстоянии rA от оси вращения (рис.
11.6, 11.7).
Путь точки A:
SA = ωrA
Линейная скорость точки A: vA = ωrA
Ускорения точки A: at A
an A = ω2rA
= εrA — касательное;
— нормальное,
где rA — радиус окружности, траектории точки А.
184.
185.
186.
187.
188.
189. Занятие 12. (2 часа) Сложное движение точки. Сложное движение твердого тела.
190.
12.1. Основные определенияСложным движением считают движение, которое можно разложить
на несколько простых. Простыми движениями считают
поступательное и вращательное.
Для рассмотрения сложного движения точки выбирают две
системы отсчета: подвижную и неподвижную.
Движение точки (тела) относительно неподвижной системы
отсчета называют сложным, или абсолютным.
Подвижную систему отсчета обычно связывают с движущимся
телом. Движение подвижной системы отсчета относительно
неподвижной называют переносным.
Движение материальной точки (тела) по отношению к подвижной
системе называют относительным.
Примером может служить движение человека по эскалатору
метро. Движение эскалатора — переносное движение,
движение человека вниз или вверх по эскалатору —
относительное, а движение по отношению к неподвижным
стенам станции — сложное (абсолютное) движение.
191.
При решении задач используют теорему о сложениискоростей:
При сложном движении точки абсолютная скорость в
каждый момент времени равна геометрической
сумме переносной (ve) и относительной (vr)
скоростей:
a — угол между векторами ve и vr.
192.
12.2. Плоскопараллельное движение твердого телаПлоскопараллельным, или плоским, называется такое движение
твердого тела, при котором все точки тела перемещаются
параллельно некоторой неподвижной в рассматриваемой
системе отсчета плоскости.
Рис.12.1. Плоскопараллельное движение твердого тела
Плоскопараллельное движение можно изучать, рассматривая
любое плоское сечение тела, параллельное неподвижной
плоскости, называемой основной (рис. 12.1).
Все точки тела, расположенные на прямой, перпендикулярной к
основной плоскости, движутся одинаково.
Плоскопараллельное движение изучается двумя методами:
методом разложения сложного движения на поступательное и
вращательное и методом мгновенных центров скоростей.
193.
а) Метод разложения сложного движения на поступательное ивращательное
Плоскопараллельное движение раскладывают на два движения:
• поступательное вместе с некоторым полюсом
• вращательное относительно этого полюса.
Разложение используют для определения скорости любой точки
тела, применяя теорему о сложении скоростей (рис. 12.2).
Рис.12.2. Метод разложения сложного движения на поступательное и
вращательное
194.
• Точка А движется вместе с точкой В, а затем поворачиваетсявокруг В с угловой скоростью ω, тогда абсолютная скорость
точки А будет равна
195.
б) Метод определения мгновенного центра скоростейСкорость любой точки тела можно определять с помощью
мгновенного центра скоростей.
При этом сложное движение представляют в виде цепи вращений
вокруг разных центров.
Задача сводится к определению положения мгновенного центра
вращений (скоростей) (рис. 12.4).
Рис.12.4. Метод определения мгновенного центра скоростей
196.
Мгновенным центром скоростей (МЦС) являетсяточка на плоскости, абсолютная скорость которой в
данный момент равна нулю.
Вокруг этой точки тело совершает поворот со
скоростью ω
Скорость точки А в данный момент равна
vA = ωОА,
т.к. vA — линейная скорость точки А, вращающейся
вокруг МЦС.
Существуют три способа определения положения
мгновенного центра скоростей.
197.
Первый способ.Известна скорость одной точки тела vA
и угловая скорость вращения тела
ω (рис. 12.5).
Точку О находим на перпендикуляре к
вектору скорости vA
Соединяем точку О с точкой Д
замеряем расстояние ОБ,
198.
Второй способ. Известныскорости двух точек тела vA и
vВ и они не параллельны
(рис. 12.6).
Проводим из точек А и В два
перпендикуляра к известным
векторам скоростей.
На пересечении
перпендикуляров находим
МЦС.
Далее можно
найти скорость любой точки С.
199.
Третий способ. Известны скорости двух точек тела, и онипараллельны (vA || vВ) (рис. 12.7).
Соединяем концы векторов, МЦС находится на пересечении
линии, соединяющей концы векторов с линией АВ (рис. 12.7).
При поступательном движении тела (рис. 12.7в) МЦС
отсутствует.
200.
201.
202. Занятие 13. (2 часа) Основные понятия и аксиомы динамики. Понятия о трении.
203.
13.1. Содержание и задачи динамикиДинамика — раздел теоретической механики, в котором
устанавливается связь между движением тел и действующими на них
силами.
В динамике решают два типа задач:
— определяют параметры движения по заданным силам;
— определяют силы, действующие на тело, по заданным
кинематическим параметрам движения.
При поступательном движении все точки тела движутся одинаково,
поэтому тело можно принять за материальную точку.
Если размеры тела малы по сравнению с траекторией, его тоже
можно рассматривать как материальную точку, при этом точка
совпадает с центром тяжести тела.
При вращательном движении тела точки могут двигаться
неодинаково, в этом случае некоторые положения динамики можно
применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
Поэтому динамику делят на динамику точки и динамику
материальной системы.
204.
13.2. Аксиомы динамикиа) Первая аксиома (принцип инерции)
Всякая изолированная материальная точка
находится в состоянии покоя или равномерного и
прямолинейного движения, пока приложенные силы
не выведут ее из этого состояния.
Это состояние называют состоянием инерции. Вывести
точку из этого состояния, т.е. сообщить ей некоторое
ускорение, может внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой
инертность является масса тела.
Массой называют количество вещества в объеме
тела, в классической механике ее считают
величиной постоянной. Единица измерения массы —
килограмм (кг).
205.
б) Вторая аксиома (второй закон Ньютона — основной закондинамики)
Зависимость между силой, действующей на материальную точку, и
сообщаемым ею ускорением следующая:
На все тела на Земле действует сила тяжести, она сообщает телу
ускорение свободного падения, направленное к центру Земли:
Где
g = 9,81 м/с 2 , ускорение свободного падения.
G – сила тяжести
206.
в) Третья аксиома (третий закон Ньютона)Силы взаимодействия двух тел равны по величине и
направлены по одной прямой в разные стороны
(рис. 13.1):
207.
г) Четвертая аксиома (закон независимости действия сил)Каждая сила системы сил действует так, как она действовала
бы одна.
Ускорение, сообщаемое точке системой сил, равно
геометрической сумме ускорений, сообщенных точке каждой
силой в отдельности (рис. 13.2):
208.
13.3. Понятие о трении. Виды тренияТрение — сопротивление, возникающее при движении одного
шероховатого тела по поверхности другого.
При скольжении тел возникает трение скольжения, при качении —
трение качения. Природа сопротивлений движению в разных
случаях различна.
а) Трение скольжения
Причина — механическое зацепление выступов. Сила
сопротивления движению при скольжении называется силой
трения скольжения (рис. 13.3а).
209.
Законы трения скольжения:Сила трения скольжения прямо пропорциональна силе
нормального давления:
где R — сила нормального давления, направлена перпендикулярно
опорной поверхности;
f — коэффициент трения скольжения.
В случае движения тела по наклонной
плоскости (рис. 13.36)
где α — угол наклона плоскости к
горизонту.
Сила трения всегда направлена в
сторону, обратную направлению
движения.
210.
2. Сила трения меняется от нуля до некоторого максимальногозначения, называемого силой трения покоя (статическое
трение):
Ffo — статическая сила трения (сила трения покоя).
3. Сила трения при движении меньше силы трения покоя.
Сила трения при движении называется динамической силой
трения (Ff )
Поскольку сила нормального давления, зависящая от веса и
направления опорной поверхности, не меняется, то
различают статический и динамический коэффициенты
трения:
211.
Коэффициент трения скольжения зависит отследующих факторов:
а) от материала:
материалы делятся на
• фрикционные (с большим коэффициентом трения)
• антифрикционные (с малым коэффициентом
трения), например f = 0,1- 0,15 (при скольжении
стали по стали всухую), f = 0,2- 3 (при скольжении
стали по текстолиту)
• от наличия смазки, например f = 0,04 - 0,05 (при
скольжении стали по стали со смазкой);
• от скорости взаимного перемещения.
212.
б) Трение каченияСопротивление при
качении связано с взаимной
деформацией грунта и
колеса и значительно
меньше трения скольжения.
Обычно считают грунт
мягче колеса, тогда в
основном деформируется
грунт, и в каждый момент
колесо должно
перекатываться через
выступ грунта.
Для равномерного качения колеса необходимо
прикладывать силу Fдв
(рис. 13.4).
213.
Условие качения колеса состоит в том, что движущийсямомент должен быть не меньше момента
сопротивления:
где k — максимальное значение плеча (половина
колеи) принимается за коэффициент трения качения,
размерность — сантиметры.
Ориентировочные значения k (определяются
экспериментально):
• сталь по стали k = 0, 005 см
• резиновая шина по шоссе — к = 0,24 см.
214.
215.
216.
217. Занятие 14. (2 часа) Движение материальной точки. Метод кинетостатики .
218.
14.1. Свободная и несвободная точкиМатериальная точка, движение которой в пространстве
не ограничено какими-нибудь связями, называется
свободной. Задачи решаются с помощью основного
закона динамики.
Материальные точки, движение которых ограничено
связями называются несвободными.
Для несвободных точек необходимо определять
реакции связей. Эти точки движутся под действием
активных сил и ограничивающих движение реакций
связей (пассивных сил).
Несвободные материальные точки освобождаются от
связей связи заменяются их реакциями. Далее
несвободные точки можно рассматривать как
свободные (принцип освобождаемости от связей)
219.
14.2. Сила инерцииИнертность — способность сохранять свое состояние
неизменным, это внутреннее свойство всех материальных тел.
Сила инерции — сила, возникающая при разгоне или торможении
тела (материальной точки) и направленная в обратную сторону
от ускорения. Силу инерции можно измерить, она приложена к
«связям» — телам, связанным с разгоняющимся или
тормозящимся телом.
Рассчитано, что сила инерции равна
Таким образом, силы, действующие на материальные точки m1 и
m2 (рис. 14.1), при разгоне платформы соответственно равны
220.
Разгоняющееся тело (платформа с массой m (рис. 14.1)) силуинерции не воспринимает, иначе разгон платформы вообще был
бы невозможен.
При вращательном движении (криволинейном) возникающее
ускорение принято представлять в виде двух составляющих:
нормального an и касательного at (рис. 14.2).
Поэтому при рассмотрении криволинейного движения могут
возникнуть две составляющие силы инерции: нормальная и
касательная
рис. 14.2
221.
При равномерном движении по дуге всегда возникает нормальноеускорение, касательное ускорение равно нулю, поэтому
действует только нормальная составляющая силы инерции,
направленная по радиусу из центра дуги (рис. 14.3).
222.
14.3. Принцип кинетостатики (принцип Даламбера)Принцип кинетостатики используют для упрощения решения ряда
технических задач.
Реально силы инерции приложены к телам, связанным с
разгоняющимся телом (к связям).
Даламбер предложил условно прикладывать силу инерции к
активно разгоняющемуся телу. Тогда система сил,
приложенных к материальной точке, становится
уравновешенной, и можно при решении задач динамики
использовать уравнения статики.
Принцип Даламбера:
Материальная точка под действием активных сил, реакций,
связей и условно приложенной силы инерции находится в
равновесии:
223.
Порядок решения задач с использованиемпринципа Даламбера
1. Составить расчетную схему.
2. Выбрать систему координат.
3. Выяснить направление и величину ускорения.
4. Условно приложить силу инерции.
5. Составить систему уравнений равновесия.
6. Определить неизвестные величины.
224.
225.
226.
227.
228.
229.
230.
231.
232. Занятие 15. (2 часа) Работа и мощность.
233.
15.1. РаботаДля характеристики действия силы на некотором перемещении
точки ее приложения вводят понятие «работа силы».
Работа служит мерой действия силы, работа — скалярная
величина.
а) Работа постоянной силы на прямолинейном пути
Работа силы в общем случае численно равна произведению
модуля силы на длину пройденного пути и на косинус угла
между направлением силы и направлением перемещения
(рис. 15.1):
Рис.15.1. Работа постоянной силы на прямолинейном пути
234.
Единицы измерения работы: 1 Дж (джоуль)= 1 Н∙м;1 кДж (килоджоуль) = 103 Дж.
Рассмотрим частные случаи.
1.
Силы, совпадающие с направлением перемещения,
называются движущими силами. Направление вектора силы
совпадает с направлением перемещения (рис. 15.2).
В этом случае α
= 0° (cos α = 1). Тогда
235.
2. Силы, перпендикулярные направлению перемещения, работыне производят (рис. 15.3).
Сила F перпендикулярна направлению перемещения,
α = 90° (cos α = 0);
236.
Силы, направленные в обратную от направления перемещениясторону, называются силами сопротивления (рис. 15.4).
Сила F направлена в обратную от перемещения S сторону.
В этом случае α
= 180° (cos α = - 1), следовательно,
Движущие силы увеличивают модуль скорости, силы
сопротивления уменьшают скорость.
Таким образом, работа может быть положительной и
отрицательной в зависимости от направления силы и
скорости.
237.
б) Работа постоянной силы на криволинейном путиПусть точка М движется по дуге окружности и сила F составляет
некоторый угол α с касательной к окружности (рис. 15.5).
Вектор силы можно разложить на
две составляющие:
Используя принцип независимости
действия сил, определим работу
каждой из составляющих силы
отдельно:
Используя принцип независимости действия сил,
определим работу каждой из составляющих силы отдельно:
Где:
- пройденный путь
238.
Нормальная составляющая силы Fnвсегда направлена
перпендикулярно перемещению и,
следовательно, работы не
производит:
При перемещении по дуге обе
составляющие силы
разворачиваются вместе с точкой
М.
Таким образом, касательная
составляющая силы Ft всегда
совпадает по направлению с
перемещением.
Будем иметь:
Касательную силу Ft обычно
называют окружной силой.
239.
Работа при криволинейном пути — это работаокружной силы:
Произведение окружной силы на радиус
называют вращающим моментом:
Работа силы, приложенной к вращающемуся
телу, равна произведению вращающего
момента на угол поворота:
240.
в) Работа силы тяжестиРабота силы тяжести зависит только от изменения высоты и равна
произведению модуля силы тяжести на вертикальное
перемещение точки (рис. 15.6):
где Δh — изменение высоты.
При опускании работа положительна, при подъеме отрицательна.
241.
г) Работа равнодействующей силыПод действием системы сил точка массой m перемещается из
положения М1 в положение М2 (рис. 15.7).
В случае движения под действием системы сил пользуются
теоремой о работе равнодействующей.
Работа равнодействующей на некотором перемещении равна
алгебраической сумме работ системы сил на том же
перемещении
Работа равнодействующей силы
242.
243.
244.
245.
246. Занятие 16. (2 часа) Мощность. Коэффициент полезного действия. Общие теоремы динамики.
247.
16.1. МощностьДля характеристики работоспособности и быстроты совершения
работы введено понятие мощности.
Мощность — работа, выполненная в единицу времени:
Единицы измерения мощности: ватты, киловатты,
а) Мощность при поступательном движении (рис. 16.1)
248.
Учитывая, чтополучим
где F — модуль силы, действующей на тело;
vср — средняя скорость движения тела.
Средняя мощность при поступательном движении
равна произведению модуля силы на среднюю
скорость перемещения и на косинус угла между
направлениями силы и скорости.
249.
б) Мощность при вращении(рис. 16.2)
Тело движется по дуге радиусом r из
точки M1 в точку М2
Работа силы:
где Мвр - вращающий момент.
Мощность
но
где ωср — средняя
угловая скорость.
250.
Мощность силы при вращении равнапроизведению вращающего момента на
среднюю угловую скорость.
Если при выполнении работы усилие машины и
скорость движения меняются, можно
определить мощность в любой момент
времени, зная значения усилия и скорости в
данный момент.
251.
16.2. Коэффициент полезного действияКаждая машина и механизм, совершая работу, тратит
часть энергии на преодоление вредных
сопротивлений.
Таким образом, машина (механизм) кроме полезной
работы совершает еще и дополнительную работу.
Отношение полезной работы к полной работе или
полезной мощности ко всей затраченной
мощности называется коэффициентом полезного
действия (КПД):
252.
Полезная работа (мощность) расходуется на движениес заданной скоростью и определяется по формулам:
Затраченная мощность больше полезной на величину
мощности, идущей на преодоление трения в звеньях
машины, на утечки и тому подобные потери.
Чем выше КПД, тем совершеннее машина.
253.
254.
255.
256. Занятие 17. (2 часа) Контрольная работа №2
257. Раздел 2. Сопротивление материалов Занятие 18. (2 часа) Основные положения. Допущения, принятые при расчетах
258.
18.1. Основные требования к деталям и конструкциям ивиды расчетов в сопротивлении материалов
а) Механические свойства материалов
Прочность — способность не разрушаться под
нагрузкой.
Жесткость — способность незначительно
деформироваться под нагрузкой.
Выносливость — способность длительное время
выдерживать переменные нагрузки.
Устойчивость — способность сохранять
первоначальную форму упругого равновесия.
Вязкость — способность воспринимать ударные
нагрузки.
259.
б) Виды расчетовРасчет на прочность обеспечивает не разрушение
конструкции.
Расчет на жесткость обеспечивает деформации
конструкции под нагрузкой в пределах допустимых
норм.
Расчет на выносливость обеспечивает необходимую
долговечность элементов конструкции.
Расчет на устойчивость обеспечивает сохранение
необходимой формы равновесия и предотвращает
внезапное искривление длинных стержней.
Для обеспечения прочности конструкций, работающих
при ударных нагрузках (при ковке, штамповке и
подобных случаях), проводятся расчеты на удар.
260.
18.2. Основные гипотезы и допущенияПриступая к расчетам конструкции, следует решить, что в данном
случае существенно, а что можно отбросить, т. к. решение
технической задачи с полным учетом всех свойств реального
объекта невозможно.
а) Допущения о свойствах материалов
Материалы однородные — в любой точке материалы имеют
одинаковые физико-механические свойства.
Материалы представляют сплошную среду — кристаллическое
строение и микроскопические дефекты не учитываются.
Материалы изотропны — механические свойства не зависят от
направления нагружения.
Материалы обладают идеальной упругостью — полностью
восстанавливают форму и размеры после снятия нагрузки.
В реальных материалах эти допущения выполняются лишь
отчасти, но принятие таких допущений упрощает расчет. Все
упрощения принято компенсировать, введя запас прочности.
261.
б) Допущения о характере деформацииВсе материалы под нагрузкой деформируются, т. е. меняют
форму и размеры.
Характер деформации легко проследить при испытании
материалов на растяжение.
Перед испытаниями цилиндрический образец закрепляется в
захватах разрывной машины, растягивается и доводится до
разрушения. При этом записывается зависимость между
приложенным усилием и деформацией. Получают график,
называемый диаграммой растяжения. Для примера на рис. 18.1
представлена диаграмма растяжения малоуглеродистой стали.
262.
На диаграмме отмечают особые точки:• от точки 0 до точки 1 — прямая линия (деформация прямо
пропорциональна нагрузке);
• от точки 2 до точки 5 деформации быстро нарастают и образец
разрушается, разрушению предшествует появление утончения
(шейки) в точке 4.
Если прервать испытания до точки 2, образец вернется к
исходным размерам; эта область называется областью упругих
деформаций. Упругие деформации полностью исчезают после
снятия нагрузки.
При продолжении испытаний после точки 2 образец уже не
возвращается к исходным размерам, деформации начинают
накапливаться.
При выключении машины в точке А образец несколько сжимается
по линии А В, параллельной линии 01. Деформации после точки
2 называются пластическими, они полностью не исчезают;
сохранившиеся деформации называются остаточными.
263.
На участке 01 выполняется закон Гука:В пределах упругости деформации прямо
пропорциональны нагрузке.
Считают, что все материалы подчиняются закону
Гука. Поскольку упругие деформации малы по
сравнению с геометрическими размерами детали,
при расчетах считают, что размеры под нагрузкой не
изменяются.
Расчеты ведут используя принцип начальных
размеров. При работе конструкции деформации
должны оставаться упругими.
К нарушению прочности следует относить и
возникновение пластических деформаций. Хотя в
практике бывают случаи, когда местные
пластические деформации считаются допустимыми.
264.
Вид образцов при разрушении265.
Гидравлические стенды для испытания образцов266.
18.3. Классификация нагрузок и элементов конструкции18.3.1. Классификация нагрузок
а) Статические нагрузки
(рис. 18.2. а) не меняются со
временем или меняются очень
медленно. При действии
статических нагрузок проводится
расчет на прочность.
Рис. 18.2 а. Статические нагрузки
б) Повторно-переменные
нагрузки (рис. 18.2б) многократно
меняют значение или значение и
знак. Действие таких нагрузок
вызывает усталость металла.
Рис. 18.2 б. Повторно-переменные
нагрузки
267.
в) Динамические нагрузки(рис. 18.2 в) меняют свое значение в короткий
промежуток времени, они вызывают большие
ускорения и силы инерции и могут привести к
внезапному разрушению конструкции.
Рис. 18.2 в. Динамические нагрузки
268.
Из теоретической механики известно, что по способу приложениянагрузки могут быть сосредоточенными или распределенными
по поверхности.
Реально передача нагрузки между деталями происходит не в
точке, а на некоторой площадке, т. е. нагрузка является
распределенной.
Однако если площадка контакта пренебрежительно мала по
сравнению с размерами детали, силу считают сосредоточенной.
При расчетах реальных деформируемых тел в сопротивлении
материалов заменять распределенную нагрузку
сосредоточенной не следует.
Аксиомы теоретической механики в сопротивлении материалов
используются ограниченно.
Нельзя переносить пару сил в другую точку детали, перемещать
сосредоточенную силу вдоль линии действия, нельзя систему
сил заменять равнодействующей при определении
перемещений Все вышеперечисленное меняет распределение
внутренних сил в конструкции.
269.
18.3.2. Формы элементов конструкцииВсе многообразие форм сводится к трем видам по одному
признаку.
1. Брус — любое тело, у которого длина значительно больше
других размеров.
В зависимости от форм продольной оси и поперечных сечении
различают несколько видов брусьев:
— прямой брус постоянного поперечного сечения (рис. 18.3 а);
— прямой ступенчатый брус (рис. 18.3 б);
— криволинейный брус (рис. 18.Зв).
270.
2. Пластина — любое тело, у которого толщина значительноменьше других размеров (рис. 18.4).
3. Массив — тело, у которого три размера одного порядка.
271. Занятие 19. (2 часа) Основные положения. Нагрузки внешние и внутренние. Метод сечений.
272.
19.1. Общие определенияЭлементы конструкции при работе испытывают внешнее
воздействие, которое оценивается величиной внешней силы. К
внешним силам относят активные силы и реакции опор.
Под действием внешних сил в детали возникают внутренние силы
упругости, стремящиеся вернуть телу первоначальную форму и
размеры.
Внешние силы должны быть определены методами теоретической
механики, а внутренние определяются основным методом
сопротивления материалов — методом сечений.
В сопротивлении материалов тела рассматриваются в равновесии.
Для решения задач используют уравнения равновесия,
полученные в теоретической механике для тела в пространстве.
Используется система координат, связанная с телом. Чаще
продольную ось детали обозначают z, начало координат
совмещают с левым краем и размещают в центре тяжести
сечения.
273.
19.2. Метод сеченийМетод сечений заключается в мысленном
рассечении тела плоскостью и
рассмотрении равновесия любой из
отсеченных частей.
Если все тело находится в равновесии, то и
каждая его часть находится в равновесии под
действием внешних и внутренних сил.
Внутренние силы определяются из уравнений
равновесия, составленных для
рассматриваемой части тела.
274.
Рассекаем тело поперек плоскостью (рис. 19.1). Рассматриваемправую часть. На нее действуют внешние силы F4; F5; F6 и
внутренние силы упругости qk , распределенные по сечению.
Систему распределенных сил можно заменить главным
вектором Rо, помещенным в центр тяжести сечения, и
суммарным моментом сил Mo:
Рис. 19.1. Метод сечений
275.
Разложив главный вектор Rq по осям, получим три составляющие:где
Nz — продольная сила;
Qx — поперечная сила по оси х;
Qy — поперечная сила по оси у.
Главный момент тоже принято представлять в виде моментов пар
сил в трех плоскостях проекции:
где:
Мх — момент сил относительно Ох;
Му — момент сил относительно Оу;
Мz — момент сил относительно Oz.
276.
Полученные составляющие сил упругости носят названиевнутренних силовых факторов.
Каждый из внутренних силовых факторов вызывает определенную
деформацию детали. Внутренние силовые факторы
уравновешивают приложенные к этому элементу детали
внешние силы.
Используя шесть уравнений равновесия, можно получить величину
внутренних силовых факторов:
277.
Из приведенных уравнений следует, что:Nz — продольная сила, равная алгебраической сумме проекций на
ось Oz внешних сил, действующих на отсеченную часть бруса;
вызывает растяжение или сжатие;
Qx — поперечная сила, равная алгебраической сумме проекций на
ось Ох внешних сил, действующих на отсеченную часть;
Qy — поперечная сила, равная алгебраической сумме проекций на
ось Оу внешних сил, действующих на отсеченную часть;
силы Qx и Qy вызывают сдвиг сечения;
Mz — крутящийся момент, равный алгебраической сумме
моментов внешних сил относительно продольной оси Oz;
вызывает скручивание бруса;
Мх — изгибающий момент, равный алгебраической сумме
моментов внешних сил относительно оси Ох;
Му — изгибающий момент, равный алгебраической сумме
моментов внешних сил относительно оси Оу;
моменты Мх и Му вызывают изгиб бруса в соответствующей
плоскости.
278.
19.3. Напряжения.Метод сечений позволяет определить величину
внутреннего силового фактора в сечении, но не дает
возможности установить закон распределения
внутренних сил по сечению.
Для оценки прочности необходимо определить
величину силы, приходящуюся на любую точку
поперечного сечения.
Величину интенсивности внутренних сил в точке
поперечного сечения называют механическим
напряжением.
Напряжение характеризует величину внутренней силы,
приходящейся на единицу площади поперечного
сечения.
279.
Рассмотрим брус, к которому приложена внешняя нагрузка(рис. 19.2).
С помощью метода сечений рассечем брус поперечной
плоскостью, отбросим левую часть и рассмотрим равновесие
оставшейся правой части.
Выделим на секущей плоскости малую площадку ΔА. На этой
площадке действует равнодействующая внутренних сил
упругости.
Направление напряжения рср совпадает с направлением
внутренней силы в этом сечении.
280.
Вектор рср называют полным напряжением. Его принятораскладывать на два вектора
(рис. 19.3):
τ — лежащий в площадке сечения
σ — направленный перпендикулярно площадке.
Если вектор p — пространственный, то его раскладывают на три
составляющие:
281.
Нормальное напряжение характеризует сопротивление сечениярастяжению или сжатию.
Касательное напряжение характеризует сопротивление сечения
сдвигу.
Сила N (продольная) вызывает появление нормального
напряжения σ
Силы Qx и Qy вызывают появление касательных напряжений τ.
Моменты изгибающие Мх и Му вызывают появление нормальных
напряжений σ, переменных по сечению.
Крутящий момент Мz вызывает сдвиг сечения вокруг продольной
оси, поэтому появляются касательные напряжения τ.
282.
283.
284. Занятие 20. Растяжение и сжатие. Внутренние силовые факторы. Напряжение. Построение эпюр.
285.
20.1. Растяжение и сжатиеРастяжением или сжатием называют вид нагружения, при
котором в поперечном сечении бруса возникает только один
внутренний силовой фактор — продольная сила.
Продольные силы меняются по длине бруса. При расчетах после
определения величин продольных сил по сечениям строится
график — эпюра продольных сил.
Условно назначают знак продольной силы.
Если продольная сила направлена от сечения, то брус растянут.
Растяжение считают положительной деформацией (рис. 20.1а).
Если продольная сила направлена к сечению, то брус сжат.
Сжатие считают отрицательной деформацией (рис. 20.1б).
286.
20.2. Примеры построения эпюрыпродольных сил
Рассмотрим брус, нагруженный
внешними силами вдоль оси.
Брус закреплен в стене (закрепление
«заделка») (рис. 20.2а).
Делим брус на участки нагружения.
Участком нагружения считают часть
бруса между внешними силами
На представленном рисунке 3 участка
нагружения.
Воспользуемся методом сечении и
определим внутренние силовые
факторы внутри каждого участка.
Расчет начинаем со свободного
конца бруса, чтобы не определять
величины реакций в опорах.
287.
Участок 1:Продольная сила положительна, участок 1 растянут.
Участок 2:
Продольная сила положительна, участок 2 растянут.
Участок 3:
Продольная сила отрицательна, участок 3 сжат. Полученное
значение N3 равно реакции в заделке.
288.
Продольная сила отрицательна, участок 3 сжат. Полученноезначение N3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.2б).
Рис.20.2.б. Эпюра продольной силы.
Эпюрой продольной силы называется график распределения
продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией.
Значения сил откладывают от оси, положительные — вверх
отрицательные — вниз.
В пределах одного участка значение силы не меняется, поэтому
эпюра очерчивается отрезками прямых линий, параллельными
оси Oz.
289.
Правило контроля: в месте приложения внешнейсилы на эпюре должен быть скачок на величину
приложенной силы.
На эпюре проставляются значения Nz. Величины
продольных сил откладывают в заранее выбранном
масштабе.
Эпюра по контуру обводится толстой линией и
заштриховывается поперек оси.
Изучая деформации при растяжении и сжатии,
обнаруживаем, что выполняются гипотеза плоских
сечений и принцип смягчения граничных условий.
Гипотеза плоских сечений заключается в том, что
поперечное сечение бруса, плоское и
перпендикулярное продольной оси, после
деформации остается плоским и перпендикулярным
продольной оси.
290.
Следовательно, продольные внутренниеволокна удлиняются одинаково, а
внутренние силы упругости
распределены по сечению равномерно.
Принцип смягчения граничных условий
гласит: в точках тела, удаленных от
мест приложения нагрузки, модуль
внутренних сил мало зависит от
способа закрепления.
Поэтому при решении задач не уточняют
способ закрепления.
291.
20.3. Напряжения при растяжении и сжатииПри растяжении и сжатии в сечении действует только нормальное
напряжение.
Напряжения в поперечных сечениях могут рассматриваться как
силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении
совпадают с направлением и знаком силы в сечении
(рис. 20.3).
292.
Исходя из гипотезы плоских сечений, можнопредположить, что напряжения при растяжении и
сжатии в пределах каждого сечения не меняются.
Поэтому напряжение можно рассчитать по формуле
где
Nz — продольная сила в сечении;
А — площадь поперечного сечения.
Величина напряжения прямо пропорциональна
продольной силе и обратно пропорциональна
площади поперечного сечения.
293.
Нормальные напряжения действуют при растяжении от сечения(рис. 20.4а), а при сжатии к сечению (рис. 20.46).
Размерность (единица измерения) напряжений — Н/м2 (Па),
однако это слишком малая единица, и практически напряжения
рассчитывают в Н/мм2 (МПа):
При определении напряжений брус разбивают на участки
нагружений, в пределах которых продольные силы не
изменяются, и учитывают места изменений площади
поперечных сечений.
Рассчитывают напряжения по сечениям, и расчет оформляют в
виде эпюры нормальных напряжений.
Строится и оформляется такая эпюра так же, как и эпюра
продольных сил.
294.
Рассмотрим брус, нагруженныйвнешними силами вдоль оси
(рис. 20.5).
Обнаруживаем три участка
нагружения и определяем
величины продольных сил.
Участок 1:
N1 = 0.
Внутренние продольные
силы равны нулю.
Участок 2:
N2 = 2F.
Продольная сила на
участке положительна.
Участок 3:
N3 = 2F - 3F = - F.
Продольная сила на
участке отрицательна.
Рис.20.5. Эпюра нормальных напряжений.
295.
Брус — ступенчатый.С учетом изменений величин площади поперечного
сечения участков напряжений больше.
Строим эпюры продольных сил и нормальных
напряжений.
Масштабы эпюр могут быть разными и выбираются
исходя из удобства построения.
296.
297.
298.
299.
300. Занятие 21. (2 часа) Растяжение и сжатие. Продольные и поперечные деформации. Закон Гука
301.
21.1. Деформации при растяжении и сжатииРассмотрим деформацию бруса под действием продольной силы
F (рис. 21.1).
Начальные размеры бруса:
lo— начальная длина,
αо — начальная ширина.
Брус удлиняется на величину Δl;
Δl— абсолютное удлинение.
При растяжении поперечные размеры уменьшаются,
Δα — абсолютное сужение;
Δl > 0; Δα < 0.
При сжатии выполняется соотношение Δl < 0; Δα > 0.
302.
В сопротивлении материалов принято рассчитывать деформациив относительных единицах:
ε — относительное удлинение;
ε' — относительное сужение.
Между продольной и поперечной деформациями существует
зависимость
где μ — коэффициент поперечной деформации, или коэффициент
Пуассона, —характеристика пластичности материала.
303.
21.2. Закон ГукаВ пределах упругих деформаций деформации прямо
пропорциональны нагрузке:
где F — действующая нагрузка; k — коэффициент.
В современной форме:
Получим зависимость
где Е — модуль упругости, характеризует жесткость материала.
В пределах упругости нормальные напряжения
пропорциональны относительному удлинению.
Значение Е для сталей в пределах (2…2,1) • 105 МПа.
При прочих равных условиях, чем жестче материал, тем меньше
он деформируется:
304.
21.3. Формулы для расчета перемещений поперечных сеченийбруса при растяжении и сжатии
Закон Гука
Откуда
Относительное удлинение
В результате получим зависимость между нагрузкой, размерами
бруса и возникающей деформацией:
где Δl — абсолютное удлинение, мм;
σ — нормальное напряжение, МПа;
l — начальная длина, мм;
Е — модуль упругости материала, МПа;
N — продольная сила, Н;
А — площадь поперечного сечения, мм2;
Произведение АЕ называют
жесткостью сечения.
305.
21.4. Выводы1. Абсолютное удлинение бруса прямо
пропорционально величине продольной силы в
сечении, длине бруса и обратно пропорционально
площади поперечного сечения и модулю упругости.
2. Связь между продольной и поперечной
деформациями зависит от свойств материала, связь
определяется коэффициентом, Пуассона,
называемом коэффициентом поперечной
деформации.
Коэффициент Пуассона:
у стали μ от 0,25 до 0,3 10-5 МПа. (2 )
• у пробки μ = 0:
• у резины μ = 0,5.
306.
3. Поперечные деформации меньше продольных и редко влияютна работоспособность детали; при необходимости поперечная
деформация рассчитывается через продольную.
где
Δα — поперечное сужение, мм;
α0 — начальный поперечный размер, мм.
4. Закон Гука выполняется в зоне упругих деформаций, которая
определяется при испытаниях на растяжение по диаграмме
растяжения (рис. 21.2).
307.
При работе пластические деформации не должнывозникать, упругие деформации малы по
сравнению с геометрическими размерами тела.
Основные расчеты в сопротивлении материалов
проводятся в зоне упругих деформации, где
действует закон Гука.
На диаграмме (рис. 21.2) закон Гука действует от точки
0 до точки 1.
5. Определение деформации бруса под нагрузкой и
сравнение ее с допускаемой (не нарушающей
работоспособности бруса) называют расчетом на
жесткость.
308.
309.
310.
311. Занятие 22. (2 часа) Механические испытания, механические характеристики. Предельные и допускаемые напряжения.
312.
22.1. Механические испытания. Статические испытания нарастяжение и сжатие
Это стандартные испытания: оборудование — стандартная
разрывная машина, стандартный образец (круглый или
плоский), стандартная методика расчета.
На рис. 22.1 представлена схема испытаний
На схеме обозначены:
do — начальный диаметр поперечного сечения;
lо — начальная длина.
313.
На рис. 22.2 изображена схема образцадо (рис. 22.2а) и после (рис. 22.26) испытаний
dш - диаметр шейки, сужения перед разрывом.
Образец закрепляется в зажимах разрывной машины и
растягивается до разрыва.
314.
Машина снабжена прибором для автоматическойзаписи диаграммы растяжения — зависимости между
нагрузкой и абсолютным удлинением (рис. 22.3)
Рис. 22.3 . Диаграмма растяжения для малоуглеродистой стали.
315.
Полученная диаграмма пересчитывается иперестраивается (рис. 22.4 — приведенная
диаграмма растяжения первого типа).
Рис.22.4. Приведенная диаграмма растяжения первого типа
316.
1) точка 1 соответствует пределу пропорциональности: после неепрямая линия (прямая пропорциональность) заканчивается и
переходит в кривую;
участок 01 — удлинение Δl растет пропорционально нагрузке;
подтверждается закон Гука;
2) точка 2 соответствует пределу упругости материала: материал
теряет упругие свойства — способность вернуться к исходным
размерам;
317.
3) точка 3 является концом участка, на котором образец сильнодеформируется без увеличения нагрузки. Это явление
называют текучестью; текучесть — удлинение при постоянной
нагрузке;
4) точка 4 соответствует максимальной нагрузке, в этот момент па
образце образуется «шейка» — резкое уменьшение площади
поперечного сечения. Напряжение в этой точке называют
временным сопротивлением разрыву, или условным пределом
прочности. Зона 3-4 называется зоной упрочнения.
318.
22.2. Механические характеристикиПри построении приведенной диаграммы рассчитываются
величины, имеющие условный характер, усилия в каждой из
точек делят на величину начальной площади поперечного
сечения, хотя в каждый момент идет деформация и площадь
образца уменьшается.
а) Основные характеристики прочности:
1. предел пропорциональности
2.предел упругости
3. предел текучести
4. предел прочности,
или временное сопротивление разрыву,
Где:
— начальная площадь сечения.
319.
б) Характеристики пластичности материалаδ — максимальное удлинение в момент разрыва
где Δl max — максимальное остаточное удлинение (рис. 22.3);
ψ — максимальное сужение при разрыве
где Аш — площадь образца в месте разрыва.
Характеристики пластичности определяют способность материала
к деформированию, чем выше значения δ и ψ, тем материал
пластичнее.
320.
22.3. Виды диаграмм растяженияРазличные материалы по-разному ведут себя под нагрузкой,
характер деформаций и разрушения зависит от типа материалов.
Принято делить материалы по типу их диаграмм растяжения на
три группы.
К первой группе относят пластичные материалы, эти
материалы имеют на диаграмме растяжения площадку текучести
(диаграммы первого типа) (рис. 22.5а).
321.
Ко второй группе относятсяхрупкие материалы, эти
материалы мало
деформируются,
разрушаются по хрупкому
типу. На диаграмме нет
площадки текучести (рис.
22.5 б).
К третьей группе относят
материалы, не имеющие
площадку текучести, но
значительно
деформирующиеся под
нагрузкой, их называют
пластично-хрупкими
(рис. 22.5в).
322.
Таким образом, хрупкий и пластично-хрупкийматериалы не имеют площадки текучести, а в
справочниках отсутствует характеристика «предел
текучести». По этой особенности их можно узнать.
Пластично-хрупкие материалы значительно
деформируются, этого нельзя допустить в
работающей конструкции. Поэтому их деформацию
обычно ограничивают. Максимально возможная
относительная деформация ε = 0,2 %.
По величине максимально возможной деформации
определяется соответствующее нормальное
напряжение σ0,2, которое принимают за предельное.
323.
22.4. Предельные и допустимые напряженияПредельным напряжением считают напряжение, при котором в
материале возникает опасное состояние (разрушение или
опасная деформация).
Для пластичных материалов предельным напряжением считают
предел текучести, т. к. возникающие пластические деформации
не исчезают после снятия нагрузки:
Для хрупких материалов, где пластические деформации
отсутствуют, а разрушение возникает по хрупкому типу (шейки
не образуется), за предельное напряжение принимают предел
прочности:
324.
Для пластично-хрупких материалов предельным напряжениемсчитают напряжение, соответствующее максимальной
деформации 0,2% (σ0,2):
Допускаемое напряжение — максимальное напряжение, при
котором материал должен нормально работать.
Допускаемые напряжения получают по предельным с учетом
запаса прочности:
где:
[σ] — допускаемое напряжение;
s — коэффициент запаса прочности;
[s] — допускаемый коэффициент запаса прочности.
325.
Примечание. В квадратных скобках принятообозначать допускаемое значение величины.
Допускаемый коэффициент запаса прочности
зависит от качества материала, условий
работы детали, назначения детали, точности
обработки и расчета и т. д.
Он может колебаться от 1,25 для простых
деталей до 12,5 для сложных деталей,
работающих при переменных нагрузках в
условиях ударов и вибраций.
326.
22.5. Расчеты на прочность при растяжении и сжатииРасчеты на прочность ведутся по условиям прочности —
неравенствам, выполнение которых гарантирует прочность
детали при данных условиях.
Для обеспечения прочности расчетное напряжение не должно
превышать допускаемого напряжения:
Расчетное напряжение σ зависит от нагрузки и размеров
поперечного сечения,
допускаемое только от материала детали и условий работы.
327.
Существуют три вида расчета на прочность.1. Проектировочный расчет — задана
расчетная схема и нагрузки; материал
или размеры детали подбираются:
— определение размеров поперечного
сечения:
— подбор материала
(по величине σпред можно подобрать марку
материала.)
2. Проверочный расчет — известны
нагрузки, материал, размеры детали;
необходимо проверить, обеспечена ли
прочность.
Проверяется неравенство
3. Определение нагрузочной
способности (максимальной
нагрузки):
328.
329.
330. Занятие 23. (2 часа) Кручение. Внутренние силовые факторы. Построение эпюр крутящих моментов. Расчеты на прочность и жесткость
331.
23.1. Деформации при крученииКручение круглого бруса происходит при нагружении его парами
сил с моментами в плоскостях, перпендикулярных продольной
оси. При этом образующие бруса искривляются и
разворачиваются на угол γ, называемый углом сдвига (угол
поворота образующей).
Поперечные сечения разворачиваются на угол φ, называемый
углом закручивания (угол поворота сечения, рис. 23.1).
рис. 23.1
Длина бруса и размеры поперечного сечения при кручении не
изменяются.
332.
Связь между угловыми деформациями определяетсясоотношением
l — длина бруса;
R — радиус сечения.
Длина бруса значительно больше радиуса сечения,
следовательно, φ >> γ.
Угловые деформации при кручении рассчитываются в
радианах.
333.
23.2. Гипотезы при кручении1. Выполняется гипотеза плоских сечений: поперечное
сечение бруса, плоское и перпендикулярное
продольной оси, после деформации остается
плоским и перпендикулярным продольной оси.
2. Радиус, проведенный из центра поперечного сечения
бруса, после деформации остается прямой линией
(не искривляется).
3. Расстояние между поперечными сечениями после
деформации не меняется. Ось бруса не
искривляется, диаметры поперечных сечений не
меняются.
334.
23.3. Внутренние силовые факторы при крученииКручением называется нагружение, при котором в поперечном
сечении бруса возникает только один внутренний силовой
фактор — крутящий момент.
Внешними нагрузками также являются две противоположно
направленные пары сил.
Рассмотрим внутренние силовые факторы при кручении круглого
бруса (рис. 23.1).
Для этого рассечем брус плоскостью I и рассмотрим равновесие
отсеченной части (рис. 23.1а).
Сечение рассматриваем со стороны
отброшенной части.
335.
Внешний момент пары силразворачивает участок бруса против
часовой стрелки, внутренние силы
упругости сопротивляются повороту.
В каждой точке сечения
возникает поперечная сила dQ (рис.
23.1б).
Каждая точка сечения имеет
симметричную, где возникает
поперечная сила, направленная в
обратную сторону. Эти силы
образуют пару с моментом
р — расстояние от точки до
центра сечения.
Сумма поперечных сил в сечении
равна нулю: ΣdQ = 0.
Рис.23.1.б.
_
Рис.23.1.в.
336.
С помощью интегрирования получим суммарный момент силупругости, называемый крутящим моментом:
Практически крутящий момент определяется из условия
равновесия отсеченной части бруса.
Крутящий момент в сечении равен сумме моментов
внешних сил, действующих на отсеченную часть
(рис. 23.1в):
337.
23.4. Эпюры крутящих моментовКрутящие моменты могут меняться вдоль оси бруса. После
определения величин моментов по сечениям строим графикэпюру крутящих моментов вдоль оси бруса.
Крутящий момент считаем положительным, если моменты
внешних пар сил направлены по часовой стрелке, в этом
случае момент внутренних сил упругости направлен против
часовой стрелки (рис. 23.2).
Рис. 23.2
Порядок построения эпюры моментов аналогичен построению
эпюр продольных сил. Ось эпюры параллельна оси бруса,
значения моментов откладывают от оси вверх или вниз,
масштаб построения выдерживать обязательно.
338.
Примеры решения задачПример 1. На распределительном валу (рис. 23.3) установлены
четыре шкива, на вал через шкив 1 подается мощность 12 кВт,
которая через шкивы 2, 3, 4 передается потребителю;
мощности распределяются следующим образом:
P2 = 8 кВт, Р3 = 3 кВт, Р4 =1 кВт, вал вращается с постоянной
скоростью ω = 25 рад/с. Построить эпюру крутящих моментов на
валу.
рис. 23.3
339.
340.
341.
342.
23.5. Напряжения при крученииПроводим на поверхности бруса сетку из продольных и
поперечных линий и рассмотрим рисунок, образовавшийся на
поверхности после деформации (рис. 23.5 а). Поперечные
окружности, оставаясь плоскими, поворачиваются на угол φ,
продольные линии искривляются, прямоугольники
превращаются в параллелограммы
343.
Рассмотрим элемент бруса 1234 после деформации.Рис.23.5.
При выводе формул используем закон Гука при сдвиге и гипотезу
плоских сечений и неискривления радиусов поперечных
сечений. При кручении возникает напряженное состояние,
называемое «чистый сдвиг» (рис.23.5 б).
При сдвиге на боковой поверхности элемента 1234 возникают
касательные напряжения, равные по величине (рис. 23.5 в),
элемент деформируется (рис. 23.5 г).
344.
Материал подчиняется закону Гука.Касательное напряжение пропорционально
углу сдвига.
Закон Гука при сдвиге
G — модуль упругости при сдвиге, Н/мм2;
γ — угол сдвига, рад.
345.
23.6. Максимальные напряжения при крученииДля круглого сечения
Для кольцевого сечения
Где:
Wp - момент сопротивления при кручении или полярный
момент сопротивления.
d – диаметр бруса круглого сечения.
346.
Условие прочности при кручении1. Разрушение бруса при кручении происходит с
поверхности, при расчете на прочность используют
условие прочности
где [τк] — допускаемое напряжение кручения
347.
23.7. Виды расчетов на прочностьСуществует три вида расчетов на прочность:
а) Проектировочный расчет — определяется диаметр бруса
[вала) в опасном сечении:
Откуда
б) Проверочный расчет — проверяется выполнение условия
прочности
в) Определение нагрузочной способности (максимального
крутящего момента)
348. Занятие 24. (2 часа) Изгиб. Классификация видов изгиба. Построение эпюр поперечных сил и изгибающих моментов
349.
24.1. Основные определенияИзгибом называется такой вид нагружения, при котором в
поперечном сечении бруса возникает внутренний силовой
фактор — изгибающий момент.
Брус, работающий на изгиб, называют балкой.
Изображен брус, закрепленный справа (защемление),
нагруженный внешними силами и моментом (рис. 24.1).
рис. 24.1
350.
Плоскость, в которой расположены внешние силы и моменты,называют силовой плоскостью.
Если все силы лежат в одной плоскости, изгиб называют плоским.
Плоскость, проходящая через продольную ось бруса и одну из
главных центральных осей его поперечного сечения,
называется главной плоскостью бруса.
Рис.24.2.
351.
Если силовая плоскость совпадает с главной плоскостью бруса,изгиб называют прямым (рис. 24.1).
Если силовая плоскость не проходит через главную плоскость
бруса, изгиб называют косым изгибом (рис. 24.2).
рис. 24.1
рис. 24.2
352.
24.2. Внутренние силовыефакторы при изгибе
Рассмотрим балку, на которую
действует пара сил с
моментом m и внешняя сила
F (рис. 24.3а).
Для определения внутренних
силовых факторов
пользуемся методом
сечений.
Рассмотрим равновесие
участка 1 (рис. 24.36).
Рис. 24.3а
Рис. 24.3 б
353.
Под действием внешней пары сил участок стремитсяразвернуться по часовой стрелке. Силы упругости,
возникающие в сечении 1, удерживают участок в
равновесии.
Продольные силы упругости выше оси бруса
направлены налево, а силы ниже оси направлены
направо.
Таким образом, при равновесии участка 1 получим:
354.
Продольная сила N в сечении равна нулю. Момент сил упругостиотносительно оси Ох может быть получен, если суммировать
элементарные моменты сил упругости в сечении 1-1
относительно оси Ох:
Этот момент называют изгибающим моментом Мх = Ми.
Из схемы вала на рис. 24.3.б видно, что часть волокон (выше оси)
испытывают сжатие, а волокна ниже оси растянуты.
Следовательно, в сечении должен существовать слой не
растянутый и не сжатый, где напряжения σ равны нулю.
Такой слой называют нейтральным слоем (НС).
355.
Линия пересечения нейтрального слоя с плоскостьюпоперечного сечения бруса называют нейтральной осью.
Нейтральный слой проходит через центр тяжести сечения.
Здесь нейтральный слой совпадает с осью Oх.
Практически величина изгибающего момента в сечении
определяется из уравнения равновесия:
Таким образом, в сечении 1-1 продольная сила равна
нулю, изгибающий момент в сечении постоянен.
Изгиб, при котором в поперечном сечении бруса возникает
только изгибающий момент, называется чистым
изгибом.
356.
Рассмотрим равновесие участка бруса от свободногоконца до сечения 2 (рис. 24.3в).
Рис. 24.3 в
Запишем уравнения равновесия для участка бруса:
357.
В сечении бруса 2-2 действует поперечная сила, вызывающаясдвиг.
Изгибающий момент в сечении:
Z2 — расстояние от сечения 2 до начала координат.
Изгибающий момент зависит от
расстояния сечения до начала
координат.
Изгиб, при котором в поперечном
сечении бруса возникает изгибающий
момент и поперечная сила, называется
поперечным изгибом.
358.
Выводы• При чистом изгибе в поперечном сечении балки
возникает только изгибающий момент, постоянный
по величине.
• При поперечном изгибе в сечении возникает
изгибающий момент и поперечная сила.
• Изгибающий момент в произвольном сечении балки
численно равен алгебраической сумме моментов
всех внешних сил, приложенных к отсеченной части,
относительно рассматриваемого сечения.
• Поперечная сила в произвольном сечении балки
численно равна алгебраической сумме проекций
всех внешних сил, действующих на отсеченной части
на соответствующую ось.
359.
24.3. Построение эпюр поперечных сил иизгибающих моментов. Основные правила
построения эпюр
Эпюры поперечных сил и изгибающих
моментов можно строить, предварительно
разделив балку на участки нагружения и
составляя уравнения, выражающие
изменения Q и Мх по участкам.
Напомним, что границы участков нагружения — это
сечения, в которых приложены внешние нагрузки.
360.
Примечание : оставьте место на чертеже дляпостроения эпюр
361.
РешениеПоследовательно по участкам нагружения рассматриваем
внутренние силовые факторы в сечениях. Силовые факторы
определяем из условий равновесия отсеченной части. Для
каждого участка записываем уравнения внутренних силовых
факторов.
Используем известные правила:
• поперечная сила численно равна алгебраической сумме
проекций внешних сил на ось Оу.
• изгибающий момент численно равен алгебраической сумме
моментов внешних сил, действующих на отсеченную часть,
относительно нейтральной оси, совпадающей с осью Ох
• принятые знаки поперечных сил и изгибающих моментов
(рис. 24.5):
362.
Составим уравнения равновесия.1. Рассмотрим участок 1 (рис. 24.6.а).
рис. 24.6.а
Сила Q1 — отрицательна.
363.
Сила Q на участке 1 постоянна.Mx — отрицательный.
Изгибающий момент меняется по линейному закону,
график — прямая линия.
364.
2. Рассмотрим участок 2 (рис. 24.6.б).рис. 24.6.б
365.
366.
3. Рассмотрим участок 3 (рис. 24.6.в).Рис. 24.6.в
367.
Обращаем внимание, что для точки В получено два значенияизгибающих моментов: из уравнения для участка 2 левее точки
В и из уравнения для участка 3 — правее точки В.
Это объясняется тем, что именно в этой точке приложен внешний
момент и поэтому внутренний момент сил упругости меняется
В точках приложения внешнего момента на эпюре моментов
появится скачок, равный величине приложенного момента.
Поперечная сила в точке В для второго и третьего участков
одинакова.
Следовательно, приложение внешнего момента не отражается
на эпюре поперечных сил.
График поперечной силы на участке 3 — прямая линия.
График изменения изгибающих моментов на третьем участке
также прямая линия.
368.
4. Построение эпюр.Порядок построения эпюр остается прежним:
масштабы эпюр выбираются отдельно,
исходя из значений максимальных сил и
моментов.
Графики обводятся толстой основной линией и
заштриховываются поперек. На графиках
указываются значения поперечных сил,
изгибающих моментов и единицы
измерения.
369.
Правила построения эпюр (рис. 24.4. и рис.24.7.):370.
1. Для участка, где отсутствует распределенная нагрузка,поперечная сила постоянна, а изгибающий момент меняется по
линейному закону.
2. В частном случае, когда поперечная сила на участке равна
нулю, изгибающий момент постоянен (чистый изгиб), график —
прямая линия, параллельная продольной оси
3. В том месте, где к балке приложена внешняя сосредоточенная
сила, на эпюре Q возникает скачок на величину приложенной
силы, а на эпюре моментов — излом.
4. В сечении, где к балке приложена пара сил (сосредоточенный
момент), на эпюре Ми возникает скачок на величину момента
этой пары. Поперечная сила при этом не изменяется.
5. В сечении на конце балки поперечная сила равна приложенной
в этом сечении сосредоточенной силе или реакции в заделке.
6. На свободном конце балки или шарнирно опертом конце момент
равен нулю, за исключением случаев, когда в этом сечении
приложена пара сил (внешний момент).
371.
Пример 2.На двухопорную балку действуют сосредоточенные
силы и моменты (рис. 24.7.). Построить эпюры
поперечных сил и изгибающих моментов.
Для двухопорной балки построение эпюр начинают с
определения опорных реакций балки.
Для их определения используем систему уравнений
равновесия,
составляем два уравнения моментов относительно
шарнирных опор.
Затем проводим проверку правильности решения по
уравнению
372.
рис.24.7Решение
1. Определение реакций в опорах. Уравнения равновесия:
373.
Реакция в опоре RA направлена в обратную сторону.Проверка:
Реакции определены верно.
374.
2. Для упрощения расчетов при построении эпюр поперечным сили изгибающих моментов можно провести расчет по
характерным точкам без составления уравнений.
Для этого используют известные связи между поперечной силой и
изгибающим моментом и правила построения эпюр.
Участок 1 (от точки А до точки С).
В точке А приложена реакция RA, направленная вниз. Поперечная
сила на участке постоянна:
Момент в точке А равен нулю.
Точка С (слева). Приложена внешняя сила F1= 35 кН,
направленная вверх, — здесь возникнет скачок вверх на
величину 35 кН.
Момент в точке С (слева) может быть рассчитан по известной
зависимости
375.
Участок 2 (от точки С справа до точки B).Поперечная сила в точке С (справа) равна
В точке С приложена внешняя пара сил с моментом 80кН·м,
следовательно, здесь проявляется скачок на величину
приложенного момента:
Поперечная сила на втором участке постоянна
376.
Момент в точке B определяется по зависимостиСправа и слева от точки в момент имеет одинаковые значения.
Участок 3 (от точки B(справа) до точки D).
В точке в приложена внешняя сила RB. Здесь появляется скачок на
величину 71 кН,
Дальше по участку поперечная сила не изменяется. Момент в
точке D равен нулю, т.к. здесь не приложена внешняя пара сил:
MD = 0.
Рассмотрение поперечных сил и изгибающих моментов можно
было провести и справа налево.
377.
По полученным значениям сил и моментов строим эпюры(эпюры под схемой вала, рис. 24.7.).
рис. 24.7.).
378. Занятие 25. (2 часа) Контрольная работа №3
379. Занятие 26. (2 часа) Детали машин и механизмов.
380.
26.1. Машины и их основные элементыЛюбая машина состоит из двигательного, передаточного и
исполнительного механизмов. Например, у металлорежущего станка
двигательным механизмом является электромотор, а у автомобиля двигатель внутреннего сгорания; исполнительным механизмом (его
также называют рабочим органом) у токарного станка является
суппорт с режущим инструментом, а у автомобиля - колеса.
Передаточные механизмы преобразовывают и передают
движение от двигателя к рабочим органам.
Механизм -это внутреннее устройство машины, приводящее ее в
действие.
Детали машин - это составные части машин и механизмов,
каждая из которых изготовлена без применения сборки (например,
вал, шестерня, болт, шплинт, ходовой винт станка, гайка).
В машине можно выделить совокупность совместно работающих
деталей, которые представляют собой конструктивно обособленные
единицы, объединенные одним назначением; эти сборочные единицы
называют узлами.
381.
Две подвижно соединенные детали образуюткинематическую пару.
Кинематической парой называется подвижное
соединение двух соприкасающихся тел,
например поршень и цилиндр, вал и подшипник и др.
Тела, составляющие кинематическую пару,
называются звеньями.
Звено механизма может состоять из нескольких деталей
(отдельно изготовляемых частей механизма), не
имеющих между собой относительного движения.
По характеру соприкосновения элементов
кинематические пары делятся на два основных класса:
низшие и высшие. У низших кинематических пар
соприкосновение звеньев происходит по поверхностям,
а у высших — по линиям или точкам.
382.
Низшие кинематические пары:1)
поступательные (рис. 26.1, а, б):
а — цилиндр 1 и поршень со штоком 2;
б— ползун 1 и прямолинейные направляющие 2;
рис. 26.1
383.
Низшие кинематические пары:2) вращательные (рис. 26.1, в, г, д):
в — плоский шарнир; е — вал и подшипник; д- шаровой шарнир.
шаровой шарнир
384.
Кинематическая пара:цилиндр и поршень со
штоком .
Кинематическая пара:
ползун и направляющие
385.
Кинематическая пара:плоский шарнир
Кинематическая пара:
вал и подшипник
386.
Высшие кинематические пары:1) колесо и рельс — соприкосновение по линии (рис. 26.2., а);
2) фрикционные катки — соприкосновение по линии (рис. 26.2, б)
3) кулачковая пара с острым толкателем — соприкосновение в
точке (рис. 26.2, в).
рис. 26.2
387.
Колесо и рельсфрикционные катки
388.
кулачковая пара с толкателем389.
Кинематическойцепью
называется
связанная
система звеньев, образующих между собой
кинематические пары.
Система тел, предназначенная для преобразования
движения одного или нескольких твердых тел в
требуемое, движение других твердых тел,
называется механизмом.
Механизм обязательно имеет неподвижное 1,
ведущее 2 и ведомое 3 звенья
(рис. 26.3.).
рис. 26.3.
390.
1- направляющие. 2-ползун.3-шатун. 4-колесо. 5-оси. 6-основание
391.
Неподвижное звено называют также стойкой.Ведущим называется звено, которое передает
заданное движение.
Ведомым называется звено, воспринимающее
движение.
26.2. Детали вращательного движения
В
машинах
много
разнообразных
деталей
вращательного движения: зубчатые колеса, шкивы
ременных передач, барабаны, звездочки цепных
передач, маховики, шпиндели станков, колеса
автомобилей и гидротурбин.
Все эти вращающиеся детали устанавливают на валах
или осях.
392.
а) Оси.Осью называется деталь, предназначенная только для поддержания вращающихся деталей; оси не передают крутящего
момента.
По конструкции оси можно разделить на две основные группы:
• оси, вращающиеся в опорах вместе с насаженными на них
деталями (рис. 26.4, а);
• неподвижные оси, являющиеся опорой вращающихся на них
деталей (рис. 26.4, б).
393.
• оси, вращающиеся в опорахвместе с насаженными на них
колесами
• неподвижные оси, являющиеся
опорой вращающихся на них
деталей
394.
б) ВалыВалы, в отличие от осей, не только поддерживают вращающиеся
детали машин, но и передают крутящие моменты, поэтому их
рассчитывают на совместное действие кручения и изгиба.
Прямые валы,
Коленчатый вал
395.
Особую группу составляют гибкие валы, положениегеометрической оси которых может изменяться в пространстве.
Чаще всего оси и валы имеют две опоры, но существуют и
многоопорные трансмиссионные валы, отдельные части
которых соединяются муфтами.
Гибкий вал, приводимый
в движение
электродвигателем.
396.
Опорные части валов и осей называют цапфами (1 на рис. 26.5.),причем промежуточные цапфы называют шейками, а концевые
- шипами.
Рис.26.5. Вал.
Для соединения вала или оси с другими деталями на поверхностях
делают шпоночные пазы 4, отверстия 3; нарезают резьбу 2 и
шлицы 6 (см. рис. 26.5).
Резкие изменения сечений вала снижают его усталостную
прочность. Поэтому переход от одного сечения к другому
должен выполняться плавно, в виде галтелей 5.
397.
в) Подшипники скольжения.Подшипник скольжения состоит из двух основных элементов:
корпуса и вкладыша.
Вкладыш, являющийся рабочим элементом опоры, может быть
неподвижным относительно корпуса, подвижным и
самоустанавливающимся;
Вкладыш представляет собой втулку (из чугуна, бронзы,
древесного пластика или другого антифрикционного
материала), запрессованную в отверстие. Часто металлические
вкладыши заливают тонким слоем антифрикционного сплава
(баббита и др.).
398.
На рис. 26.6 показан разъемный подшипник. Подшипники этойгруппы состоят из корпуса 5, разрезного вкладыша 4, крышки 3
и болтов 1. Вкладыш неподвижен относительно корпуса и
крышки.
Рис.26.6 Разъемный подшипник скольжения.
Смазка поступает на трущиеся поверхности через отверстие в
крышке из смазочного резервуара — масленки 2. Износ
вкладыша компенсируется поджатием крышки с верхней
половиной вкладыша. При значительном износе вкладыш
заменяют новым.
399.
Вкладыши в подшипниках скольжения изготовляют из чугуна (прималой скорости и умеренном давлении), бронзы (для более
нагруженных подшипников и большой скорости), чугуна или
стального литья с заливкой баббитом, древесины (бакаута,
березы, акации и др.), прессованной древесины,
цельнопрессованного древесного пластика, различных
пластмасс (текстолита, капрона и др.)
400.
г) Подшипники каченияПодшипники качения — стандартные изделия, которые
изготовляются в массовом количестве на специализированных
заводах.
401.
Подшипники качения классифицируются:По направлению действия нагрузки:
1) радиальные подшипники воспринимают
преимущественно радиальную нагрузку,
действующую перпендикулярно оси вращения
подшипника (рис. 26.7, а);
2) упорные подшипники воспринимают
преимущественно осевую нагрузку, действующую
вдоль оси вращения (рис. 26.7, б),
3) радиально-упорные подшипники воспринимают
комбинированную нагрузку, одновременно
действующую на подшипник в радиальном и осевом
направлениях
402.
рис. 26.7, бРоликовый упорный
подшипник
рис. 26.7, а
Радиальный шариковый
подшипник
рис. 26.7, в
Радиально-упорный
роликоподшипник
403.
Роликоподшипники в зависимости от формы роликов разделяютсяна следующие группы:
• с короткими цилиндрическими роликами,
• с длинными цилиндрическими роликами,
• с витыми роликами,
• с игольчатыми роликами,
• с коническими
• со сферическими роликами,
Рис.26.8 Ролики для подшипников
404.
По числу рядов тел качения подшипники делятся на однорядные(см. рис.26.7, а), двухрядные (рис. 26.9), четырех- и
многорядные.
Рис.26.9. Двухрядный шариковый подшипник.
405.
Подшипники качения (см. рис.)состоят :
• из двух колец - внутреннего 1 и
наружного 2 (внутреннее кольцо
насаживается на вал, а наружное
закрепляется в корпусе
подшипника);
• тел качения — шариков 3 или
роликов, катящихся по беговым
дорожкам колец на некотором
расстоянии один от другого,
• сепаратора 4 — специальной
детали, удерживающей тела
качения на постоянном
расстоянии друг от друга.
рис. 26.7
Радиальный шариковый
подшипник
406. Занятие 27. (2 часа) Соединения деталей
407.
27.1.Разъемные соединения деталейК разъемным соединениям деталей относятся:
резьбовые,
• фрикционные с коническими кольцами,
• клиновые,
• штифтовые,
• шпоночные,
• шлицевые и профильные (бесшпоночные).
Разъемные соединения можно неоднократно
разбирать и вновь собирать..
408.
а) Резьбовые соединенияРезьбовые соединения - это разъемные соединения, выполненные
с помощью резьбовых крепежных деталей - винтов, болтов,
шпилек, гаек или резьбы, нанесенной непосредственно в
соединяемой детали.
Резьба образуется путем нанесения на поверхность деталей
винтовых канавок с сечением согласно профилю резьбы.
Образованные таким образом выступы носят название витков.
Возможны следующие профили резьб, применяемых для винтовых
передач:
• треугольный (рис. 27.1, а),
• прямоугольный (рис. 27.1, б)
• трапецеидальный (рис. 27.1, в).
рис. 27.1,
Профили резьбы
409.
Часть тела, ограниченная винтовыми поверхностями,называется резьбой. В соответствии с формой
плоской фигуры, образующей ее профиль,
различают винты с треугольной, прямоугольной,
трапецеидальной резьбой .
Профиль резьбы выбирается в зависимости от
назначения резьбового соединения.
Термин «винт» применяют как в общем
(объединяющем также болты и шпильки), так и в
частном (винт, вращаемый при завинчивании и
отвинчивании, т.е. ввинчивающийся в деталь)
смыслах.
От этого названия возникли другие термины: винтовое
движение, винтовая линия, винтовая поверхность.
Термин «резьба» произошел от технологического
процесса ее изготовления - нарезания.
410.
Болтом называется цилиндрический стержень с резьбой,имеющий головку. За головку болт вращают или, наоборот,
удерживают от вращения при соединении деталей. Нарезной
частью стержня болт ввинчивается в гайку.
Другой тип резьбового крепежного изделия — винт — отличается
от болта только тем, что ввинчивается не в гайку, а в резьбовое
отверстие одной из соединяемых деталей.
Гайка - это деталь с резьбовым отверстием, навинчиваемая на
винт и имеющая форму, приспособленную для захвата гаечным
ключом или рукой.
Рис.27.1.г. Болты с гайками и шайбами.
411.
Шпилька — цилиндрический стержень, имеющий винтовую нарезкус обоих концов. При соединении шпилькой ее ввертывают в
одну из скрепляемых деталей, а на другой конец шпильки
навинчивают гайку.
Рис.27.1.д. Шпилька
Рис.27.1.е. Обозначение резьбовых
соединений на чертежах
412.
Различают правую и левую резьбу. Если со стороны торца винтана наружной части винтовая линия поднимается слева направо,
то резьбу называют правой, если справа налево - левой.
Независимо от профиля все резьбы имеют стандартизованный
шаг винта «р» (см. рис. 27.1. ж.).
Шагом резьбы Р называется измеренное вдоль образующей
цилиндра расстояние между одноименными точками двух
соседних витков.
Это основная характеристика винта, которая показывает, на какое
расстояние (в мм) перемещается гайка (или болт) вдоль своей
оси за один оборот.
рис. 27.1. ж.
Параметры резьбы
413.
б) Клиновое соединениеКлиновое соединение - это разъемное соединение, затягиваемое
или регулируемое с помощью клина. Типичным примером
клинового соединения является соединение вала со втулкой.
Рабочие поверхности клиньев выполняют цилиндрическими или
плоскими с фасками
В силовых клиновых соединениях выбирают уклоны 1:100, 1:40,
1:30. Установочные клинья имеют уклоны 1:10, 1:6, 1:4.
414.
в) Соединения штифтами.Штифты предназначены в основном для взаимного фиксирования
деталей, а также для передачи относительно небольших
нагрузок. Применяются и специальные срезающиеся штифты,
служащие предохранительным элементом в муфтах.
Рис.27.2. Конические штифты
415.
г) Шпоночные соединенияШпонкой называют стальной стержень, вводимый
между валом и посаженной на него деталью —
зубчатым колесом, шкивом, муфтой — для взаимного
соединения и передачи вращающего момента от
вала к детали или от детали к валу.
Шпонки делятся на две основные группы:
• клиновые (с уклоном), дающие напряженные
соединения;
• призматические (без уклона), при применении
которых получаются ненапряженные соединения.
416.
К клиновым шпонкам относятся врезные, на лыске и фрикционные.Канавки для клиновых врезных шпонок 1 выполняют и в детали
2, и на валу 3 (рис. 27.3.).
Рис. 27.3. Врезная шпонка
При клиновых шпонках на лыске канавка делается только в
детали, а на валу образуется плоский срез — лыска (рис. 27.4,
а); при клиновых фрикционных шпонках (рис. 27.4, б) лыски на
валу нет.
Рис. 27.4.
а – клиновая шпонка на лыске
б - клиновая фрикционная шпонка
417.
Призматические шпонки не имеют уклона. Их закладывают в пазна валу (рис. 27.5.) Такие шпонки не удерживают деталь от
осевого смещения по валу; с этой целью используют заплечики
на валу, установочные кольца, стопорные винты и т. п.
Рис. 27.5. Призматическая шпонка.
Сегментная шпонка (рис. 27.6.) представляет собой сегментную
пластинку, заложенную закругленной стороной в паз
соответствующей формы, профрезерованный на валу.
Рис. 27.6. Сегментная шпонка.
418.
д) шлицевые (зубчатые) соединенияДля снижения концентрации напряжений, а также для лучшего
центрирования деталей на валу и уменьшения напряжений
смятия в шпоночном соединении (что особенно важно для
подвижных соединений) применяют шлицевое (или зубчатое)
соединение деталей с валом. Этот вид соединений получил в
последнее время большое распространение.
Рис.27.7. Конец вала, обработанный под шлиц.
419.
з) МуфтыМуфтами называют устройства, служащие для соединения валов
между собой или с деталями, свободно насаженными на валы
(зубчатые колеса, шкивы), с целью передачи вращающего
момента.
Муфты делятся на постоянные и сцепные.
Постоянные муфты:
• глухие, требующие строгой соосности соединяемых валов;
• компенсирующие, допускающие параллельное смещение,
взаимный перекос осей, осевое перемещение вследствие
температурных изменений длины соединяемых валов.
Компенсирующие муфты, в свою очередь, подразделяются на
жесткие, т. е. не имеющие эластичных элементов и передающие
вместе с моментом возможные толчки и удары, и упругие,
смягчающие толчки и удары.
Сцепные муфты:
• фрикционные (т. е. осуществляющие сцепление за счет сил
трения)
• кулачковые.
420.
Глухие жесткие и упругие компенсирующие муфтыВтулочные муфты (рис. 27.8) — простейшая из глухих
постоянных муфт. Это стальная или чугунная втулка,
установленная с натягом на концы соединяемых валов. Муфта
закрепляется на валах и передает момент при помощи
призматических, клиновых или сегментных шпонок или
конических штифтов. Конструкция и изготовление муфты
несложны. Недостатки втулочной муфты: трудность разборки,
необходимость очень точного совмещения осей валов.
Рис.26.8. Втулочная муфта
421.
Поперечно-свертная муфта (рис. 27.9.) также применяется длясоединения строго ссосиых валов. Муфта состоит из двух
полумуфт, имеющих форму фланцев. Полумуфты насаживают
на концы соединяемых валов и стягивают болтами.
Рис. 27.9. Поперечно-свертная муфта
422.
Продольно-свертная (или продольно-разъемная)глухая муфта состоит из двух половин, соединенных
болтами (рис. 27.10).
Рис. 27.10. Продольно-свертная муфта.
423.
Жесткие и упругие компенсирующие муфты применяют длякомпенсации погрешностей в относительном положении и
соединяемых валов; смещения центров; взаимного наклона
осей; осевого смещения.
Возможность компенсировать тот или иной вид отклонений
зависит от конструкции муфты.
Компенсирующая муфта
с упругими втулками
424.
27.2. Неразъемные соединенияК неразъемным относятся соединения, не допускающие
относительного перемещения деталей машин.
Это сварные, заклепочные и клеевые соединения; неподвижные
соединения, полученные армированием пластмассовых
деталей. Сюда можно отнести и неподвижные соединения
деталей по посадкам с натягом.
Армированные детали
Сварочное соединение
Заклепочное соединение
425.
а) Сварные соединения.Сварные соединения - это неразъемные соединения,
основанные на использовании сил молекулярного
сцепления и получаемые путем местного нагрева
изделий.
Сварка (электродуговая, электрошлаковая)
осуществляется нагревом до расплавленного
состояния, но и с применением механического усилия
(контактная сварка).
Сваркой можно изготавливать детали неограниченных
размеров.
Прочность сварных соединений доведена при статических
и ударных нагрузках до прочности целого металла.
В настоящее время освоена сварка всех конструкционных
металлов, включая высоколегированные, а также
цветных сплавов и пластмасс.
426.
По взаимному расположению соединяемых элементов сварныесоединения можно разделить на следующие группы:
• соединения встык (соединяемые элементы сваривают по
торцам, рис. 27.11.а);
рис. 27.11. а
• соединения внахлестку (поверхности соединяемых элементов
частично перекрывают друг друга);
рис. 27.11. б
427.
• соединения тавровые (соединяемые элементыперпендикулярны один к другому, при этом один элемент
приваривается торцом к боковой поверхности другого);
• соединения угловые (соединяемые элементы расположены под
углом друг к другу, привариваются по кромкам).
428.
б) Заклепочные соединенияЗаклепочные соединения образуют постановкой заклепок в
совмещенные отверстия соединяемых элементов и расклепкой
с осаживанием стержня (рис. 27.12).
Заклепка представляет собой цилиндрический металлический
стержень с головкой. В зависимости от типа головки различают
заклепки
• с полукруглой (рис. 27.12, а),
• потайной (рис. 27.12, б)
• полупотайной (рис. 27.12, в) головками.
Рис. 27.12. Заклепочные соединения.
429.
Клепка с помощью пневмоинструмента430.
Заклепки и заклепочный инструмент431.
в) Клеевое соединение.Неразъемное соединение деталей из различных материалов
можно осуществить клеями на основе синтетических смол.
Достоинствами клеевых соединений являются:
• возможность соединения деталей из разнородных, а также
тонколистовых материалов;
• хорошее сопротивление усталости;
• возможность обеспечения герметичности.
В последние годы склеивание нашло широкое применение даже в
ответственных машинах и сооружениях (самолетах, мостах), в
металлорежущих станках (для повышения износостойкости на
направляющие приклеивают фторопласт).
Основным недостатком клеевых соединений является их слабая
работа на неравномерный отрыв.
432.
Клеевые соединения и клеи433.
г) Соединение посадкой с натягом.В машиностроении для создания неподвижного соединения,
например для деталей «вал-шестерня», «вал-подшипник»
можно использовать посадки с натягом.
Они характеризуются наличием гарантированного натяга
независимо от способа соединения деталей (под прессом,
разогреванием охватывающей детали, охлаждением
охватываемой детали или комбинированным способом). Выбор
посадки производится из условия, что при наименьшем натяге
обеспечивается прочность соединения и передача нагрузки, а
при наибольшем - прочность деталей.
434.
Тяжелые посадки применяются в соединениях с большиминагрузками, например в вагонных колесах на осях,
установочных штифтах в станочных приспособлениях,
несъемных муфтах на концах валов прокатных станов, седле
клапана в головке блока цилиндров грузового автомобиля.
Тяжелая посадка шестерни турбины
435.
Средние посадки рекомендуется применятьдля запрессовки втулок в шкивы и зубчатые
колеса, соединения кондукторных втулок с
корпусом кондуктора, закрепления зубчатых
колес на валах коробок скоростей, установки
бронзовых венцов червячных колес.
Легкие посадки с натягом применяют для
соединения тонкостенных втулок с
корпусами, закрепления установочных колец
на валу электродвигателя, соединения
втулок с зубчатыми колесами
металлорежущих станков.
436. Занятие 28. (2 часа) Фрикционные передачи. Зубчатые передачи. Червячные передачи
437.
28.1. Классификация передач и их назначениеНаиболее распространенными являются передачи вращательного
движения. Это объясняется существенным преимуществом
вращательного движения по сравнению с движением
возвратно-поступательным.
Нецелесообразность, а иногда невозможность прямого
соединения двигателя и машины объясняется следующими
факторами:
• несовпадением их скоростей (двигатели обычно имеют
большие угловые скорости, что позволяет делать их
компактными, в рабочих же органах машин часто требуется
большой момент при относительно небольших скоростях);
• необходимостью изменять скорость машины при постоянной
скорости выбранного двигателя;
• необходимостью в ряде случаев одним двигателем приводить в
движение несколько механизмов.
438.
Механическиепередачи
следующим признакам:
классифицируют
по
1. по физическим условиям передачи движения:
• трением (фрикционные, ременные, канатные);
• сцеплением одного звена с другим
(зубчатые,
червячные, цепные);
2. по способу соединения ведущего и ведомого
звеньев:
• передачи с непосредственным касанием ведущего и
ведомого
звеньев
(фрикционные,
зубчатые,
червячные);
• передачи с промежуточным звеном, соединяющим
ведущее и ведомое звенья (ременные, канатные,
цепные.)
439.
28.2. Фрикционные передачиФрикционные передачи - это передачи, в которых движение от
ведущего тела к ведомому передается силами трения.
На рис. 28.1. показаны простейшие фрикционные передачи.
Рис.28.1. Фрикционные передачи
Рис.28.2. Кинематические отношения фрикционной передачи.
440.
Рис.28.2. Кинематические отношения фрикционной передачи.441.
Ведущий диск 1 поджимается силой Q к торцовой поверхностидиска 2. При вращении диска 1 в точке М возникает сила трения
Fтр = fтрQ
которая приводит во вращение ведомый диск 2.
Можно определить, с какой угловой скоростью будет вращаться
ведомый диск. Передаточное отношение определяется
отношением угловых скоростей ведомого звена к ведущему.
Для данной передачи оно определится так:
Следовательно, угловая скорость ведомого звена
442.
Если диску 1 сообщить поступательное перемещение вдоль осиN - N, то у ведомого диска 2 будет бесступенчато меняться угловая
скорость, так как радиус r2 может изменять свое значение от 0
до R.
Такие фрикционные передачи, которые позволяют бесступенчато
изменять частоту вращения ведомого звена, называются
вариаторами.
Наибольший диапазон регулирования частот вращения D =
nmax/nmin:
у лобовых вариаторов - 3...4,
у торцовых и конусно-шкивных - 8... 10.
443.
Работа фрикционного вариатора444.
Достоинства фрикционных передач:• простота тел качения;
• бесступенчатость регулирования скорости;
• возможность изменения скорости ведомого звена без остановки
ведущего, что очень важно в приводах металлорежущих
станков;
• низкая стоимость изготовления в силу простоты конструкции.
Недостатки:
• невозможность (в отличие от зубчатых зацеплений) получения
точных передаточных отношений;
• повышенный износ;
• необходимость специальных нажимных устройств (чего не
требуется зубчатым передачам); большие нагрузки на
подшипники.
445.
28.3.Ременные передачиРеменная передача (рис. 28.3, а, б) широко применяется для
передачи движения между удаленными друг от друга валами.
Она осуществляется посредством шкивов 2, закрепленных на
валах, и надетых на эти шкивы одного плоского 1 либо
нескольких клиновых ремней 3. Первая называется
плоскоременной, а вторая клиноременной передачей.
Рис.28.3. Ременные передачи
446.
Ременная передача447.
Преимуществами ременных передач являются:• возможность осуществлять передачу на
значительные расстояния;
• эластичность привода, смягчающая колебания и
нагрузки и предохраняющая от значительных
перегрузок (за счет проскальзывания);
• плавность хода и бесшумность работы.
К недостаткам относятся:
• большие габариты,
• непостоянство передаточного отношения (из-за
проскальзывания ремня на шкивах),
• большое давление на валы и подшипники.
448.
Вследствие неизбежного скольжения окружная скорость наведомом валу v2 меньше скорости vx на ведущем валу:
Отсюда передаточное отношение
В справочниках приведены следующие значения относительного
скольжения ξ:
прорезиненные, текстильные и синтетические ремни - 0,01;
кожаные ремни - 0,015;
кордтканевые клиновые ремни - 0,2;
кордшнуровые клиновые ремни - 0,01.
449.
28.3.1. Устройство и принцип работы ременного вариатора.Клиноременной вариатор состоит из ременной передачи, где шкивы
образованы коническими дисками, за счет сдвигания и раздвигания
которых изменяются диаметр шкивов и, соответственно, передаточное
число.
Из рисунка видно, что ремень в
разрезе имеет трапециевидную
форму и "вклинивается" в шкив
только своими боковыми
поверхностями.
Как изменяется передаточное число? Устройство ведущего шкива таково,
что его щеки при воздействии центробежных сил плавно сжимаются и
выталкивают клиновидный ремень все дальше и дальше от центра
шкива. Ведомый же шкив при этом наоборот, разжимается, и ремень на
нем плавно утопает все ближе и ближе к центру шкива.
Чем больше обороты двигателя - тем больше сжимается ведущий шкив и
разжимается ведомый, тем самым меняя передаточное число. Этот
процесс хорошо виден на рисунках
(рис. 28.4.)
450.
Двигатель не запущен.Малые обороты двигателя.
Средние обороты двигателя.
Максимальные обороты двигателя.
Рис.28.4.
451.
Работа клиноременного вариатора452.
28.4. Зубчатые передачиЗубчатая передача является механизмом, который с помощью
зубчатого зацепления передает или преобразует движение с
изменением угловых скоростей и моментов.
Здесь будут рассмотрены зубчатые передачи, составленные из
цилиндрических (рис. 28.4, а) и конических (рис. 28.4, б)
зубчатых колес.
Рис.28.4. Зубчатые передачи.
453.
Для передачи вращения между параллельными валамииспользуют цилиндрические зубчатые колеса (рис. 28.4, в-д).
Для преобразования и передачи вращения между валами с
пересекающимися осями используют конические зубчатые
колеса (рис. 28.4, б), а между перекрещивающимися осями зубчатовинтовые (рис. 28.4, д).
454.
455.
По сравнению с рассмотренными выше зубчатыепередачи имеют существенные преимущества:
• малые габариты,
• надежны в работе,
• долговечны,
• высокий КПД ,
• постоянное передаточное отношение,
• большой передаваемый крутящий момент. Кроме
того, они могут применяться в широком диапазоне
скоростей и моментов.
К недостаткам можно отнести:
• шум,
• ступенчатость регулирования скоростей,
• невозможность переключать скорости на ходу
456.
Передаточное отношение зубчатойпередачи равно
т. е. передаточное отношение зубчатой
передачи равно отношению чисел зубьев
ведущего зубчатого колеса к числу зубьев
ведомого.
457.
28.5. Червячные передачиЧервячная передача (рис. 28.5.) состоит из червяка, т.е. винта с
трапецеидальной резьбой, и зубчатого (червячного) колеса.
Рис.28.5. Червячная передача
Ось червячного колеса перпендикулярна оси червяка, поэтому
червячные передачи имеют характерные черты зубчатых и
винтовых передач. Червячная передача дает возможность
получать очень малые передаточные отношения (например,
1:400, 1:500.)
458.
Передаточные отношения i червячной передачи рассчитываютсяпо формуле
где
k - число заходов червяка;
z - число зубьев червячного колеса.
Недостатком червячной передачи является малый коэффициент
полезного действия, преимуществом - компактность,
бесшумность, плавность хода, возможность большого
редуцирования.
Широкое применение червячные передачи имеют в подъемнотранспортных машинах, в металлорежущих станках,
автомобилях. Материалы выбирают с учетом особенностей
работы червячной пары.
459.
28.6.Цепные передачиЦепные передачи, как и ременные, применяются для передач
между валами, удаленными друг от друга
Цепная передача состоит (рис. 28.6.) из ведущей 1 и ведомой 2
звездочек и цепи 3, охватывающей и входящей с ними в
зацепление.
Рис.28.6. Цепная передача.
Кроме перечисленных основных элементов цепные передачи
включают натяжные и смазочные устройства.
460.
Для цепных передачстанков используют
цепи двух
конструкций:
• втулочно-роликовые
(рис. 28.7, а) и
• бесшумные
(рис. 28.7, б);
последние
рекомендуются для
передачи больших
крутящих моментов.
461.
Достоинства цепных передач:• возможность передавать движение на удаленные друг от друга
валы;
• меньшие, чем у ременных передач, габаритные размеры;
• высокий КПД;
• возможность передавать вращение нескольким звездочкам;
• малые силы, действующие на валы, так как отсутствуют
первоначальные натяжные устройства;
• отсутствие скольжения;
• возможность легкой замены цепи.
Недостатки:
• повышенный износ (работают в условиях отсутствия
жидкостного трения);
• цепи вытягиваются вследствие износа шарниров, поэтому в
процессе эксплуатации приходится применять натяжные
устройства;
• при небольшом числе зубьев звездочки скорость вращения
приводной звездочки и цепи неравномерная.
462.
Передаточное отношение будет определяться, как идля зубчатой передачи, формулой
где
z1 - число зубьев ведущей звездочки,
z2 - число зубьев ведомой звездочки.
Величина, обратная передаточному отношению,
называется передаточным числом:
463.
Применение цепных передач464. Занятие 29. (2 часа) Реечные передачи. Кривошипно – шатунные передачи. Кулисные механизмы
465.
29.1. Реечные передачиРеечная передача служит для преобразования вращательного
движения в поступательное прямолинейное и наоборот.
Реечная передача (рис. 29.1.) состоит из зубчатого колеса 1 и
зубчатой рейки 2. Рейка является частным случаем зубчатого
колеса, когда радиус колеса увеличен до бесконечности.
Рис.29.1. Реечная передача.
466.
Реечная передача может бытьвыполнена с прямозубым и косозубым
зацеплением колеса с рейкой.
За один оборот прямозубого колеса с
числом зубьев z рейка переместится на
а за n об/мин зубчатого колеса – на:
Где:
Н – перемещение рейки
m – модуль зубчатой рейки
z – число зубьев рейки
π = 3,14
n – число оборотов зубчатого колеса
467.
29.2.Кривошипно-шатунные механизмыКривошипно-шатунные механизмы (см. рис. 29.2.) также
предназначены для преобразования вращательного движения в
поступательное, но они обеспечивают перемещение по
определенному закону.
Кривошипно-шатунный механизм состоит из стойки 1, кривошипа
2, шатуна 3 и ползуна 4, движущегося в направляющих 5.
Рис.29.2. Кривошипно-шатунный механизм.
468.
Кривошипно-шатунный механизм служит для преобразованиявращательного движения кривошипа в возвратнопоступательное прямолинейное движение ползуна.
Наоборот, когда ведущим звеном является ползун, возвратнопоступательное прямолинейное движение ползуна
преобразовывается во вращательное движение кривошипа и
связанного с ним вала.
Кривошипно-шатунные механизмы широко применяют в
поршневых двигателях, компрессорах, прессах, насосах и т. д.
469.
29.3. Кулисные механизмыКривошипно-кулисный механизм служит для преобразования
вращательного движения в поступательное. Наибольшее
распространение получили кулисные механизмы с качающейся
кулисой (в приводе поперечно-строгальных станков)
кулисный механизм с качающейся кулисой
470.
На рис. 29.3.представлена схема
привода с качающейся
кулисой. Кулисное колесо 1
получает вращение от
ведущего колеса zвщ. На
кулисном колесе закреплен
палец 2 с надетым на него
камнем 3. Камень вставлен
в прорезь кулисы 4 и может
скользить вдоль прорези.
Верхний конец кулисы
через серьгу 5 связан с
ползуном 6.
Рис.29.3. Кулисный механизм
471.
29.4. Кулачковые механизмыКулачковые механизмы применяют в тех случаях, когда
перемещение, скорость и ускорение ведомого звена должны,
изменяться по заранее заданному закону, в частности, когда
ведомог звено должно периодически останавливаться при
непрерывном движении ведущего звена.
Чаще всего кулачковый механизм состоит из трех звеньев (рис.
29.4, а): кулачка 1, толкателя 2 , стойки 3. На рис. 29.4., б
представлен четырехзвенный кулачковый механизм (четвертое
звено — ролик 4),
472.
Кулачковые механизмы подразделяются на плоские и'пространственные. Плоскими называют такие кулачковые
механизмы, у которых кулачок и толкатель перемещаются в
одной или параллельных плоскостях; пространственными —
такие, у которых кулачок и толкатель перемещаются в
непараллельных плоскостях.
На рис. 29.5 представлена схема пространственного
цилиндрического кулачкового механизма с профильным пазом
на боковой поверхности.
рис. 29.5










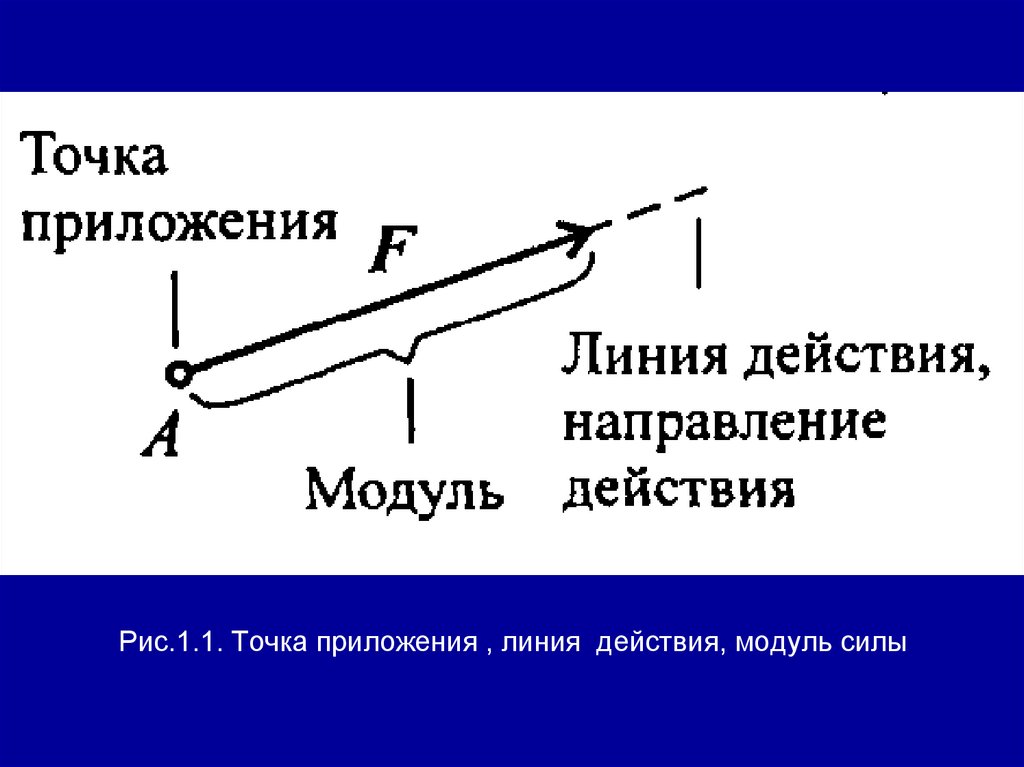


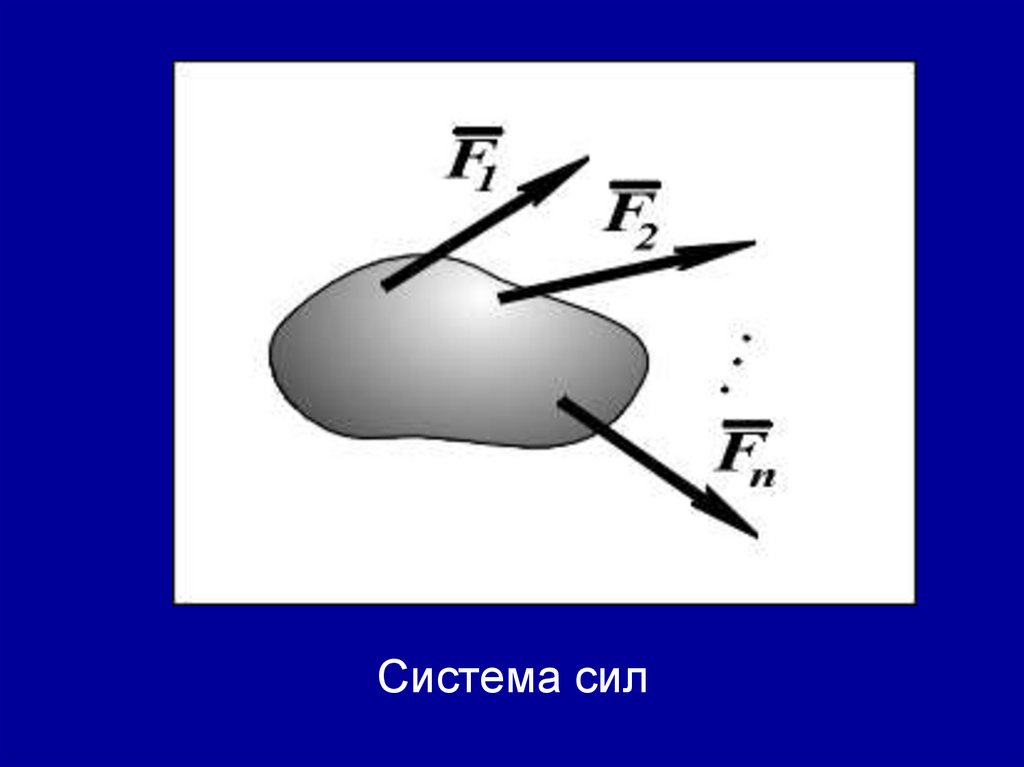

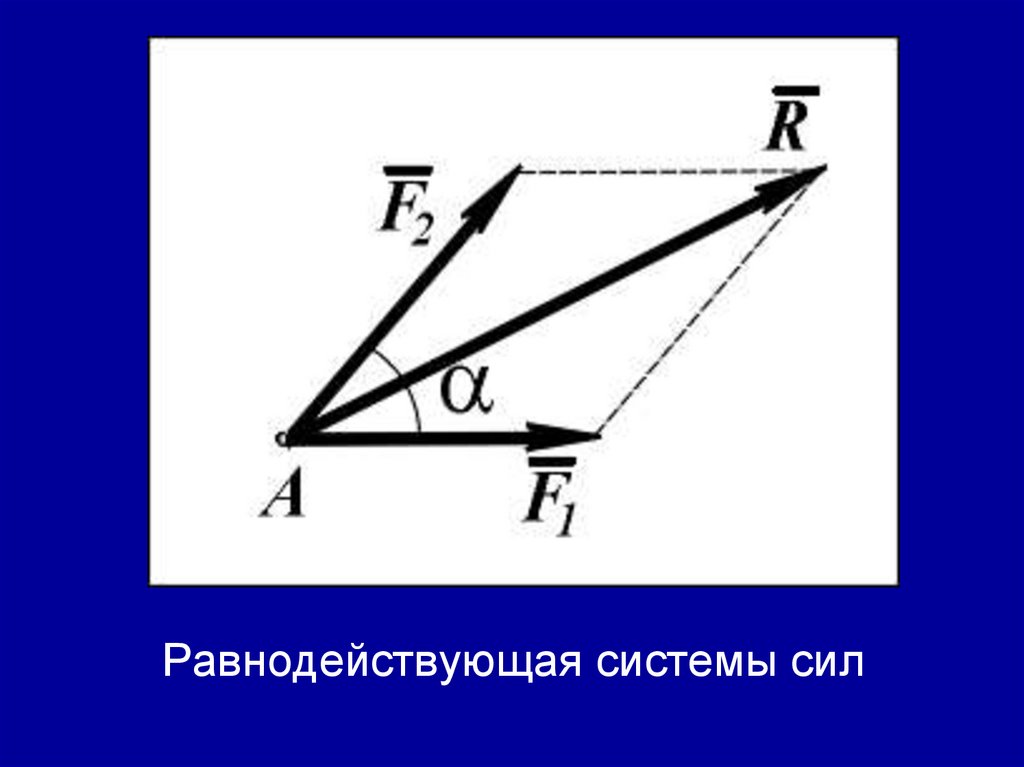


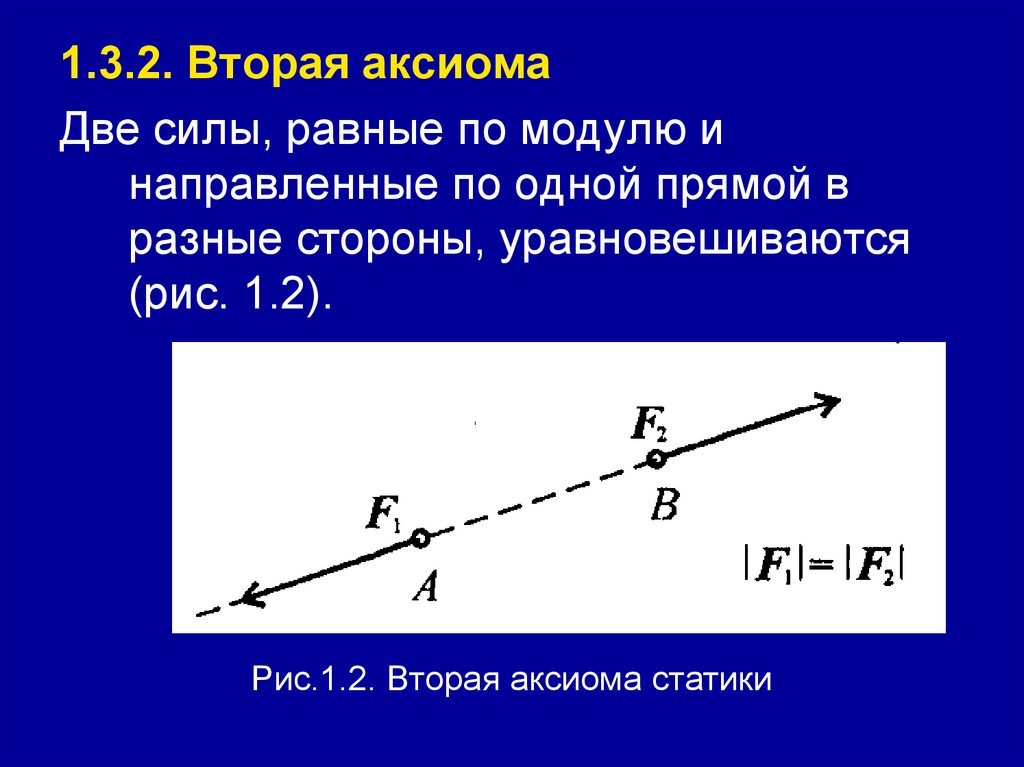
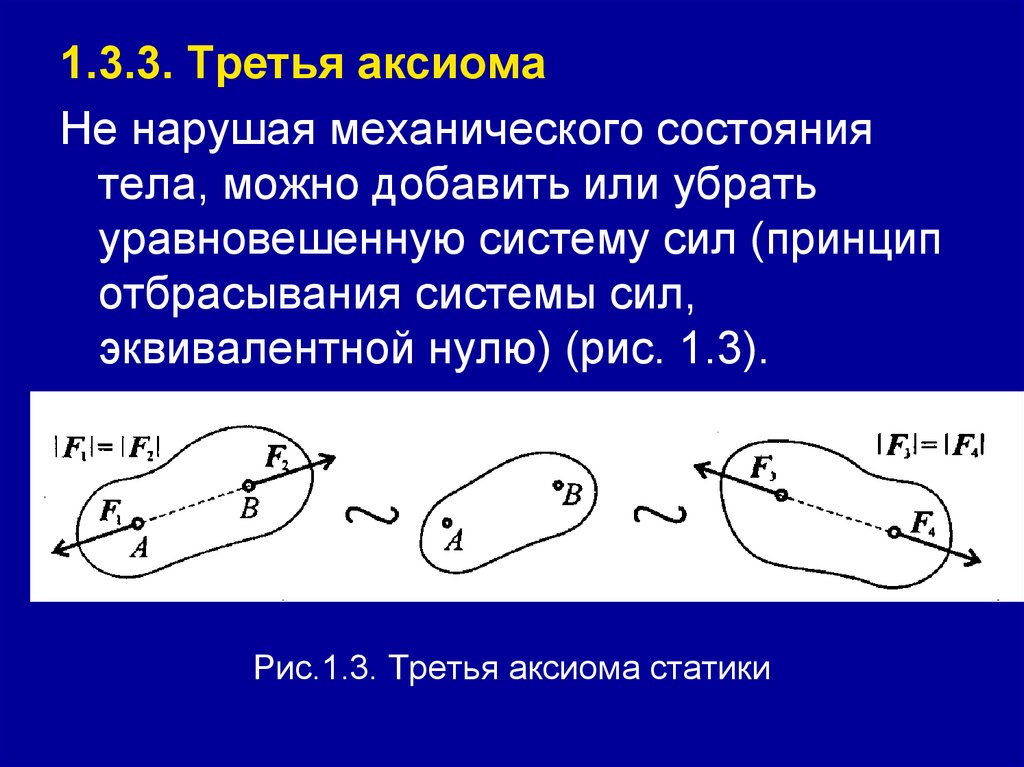
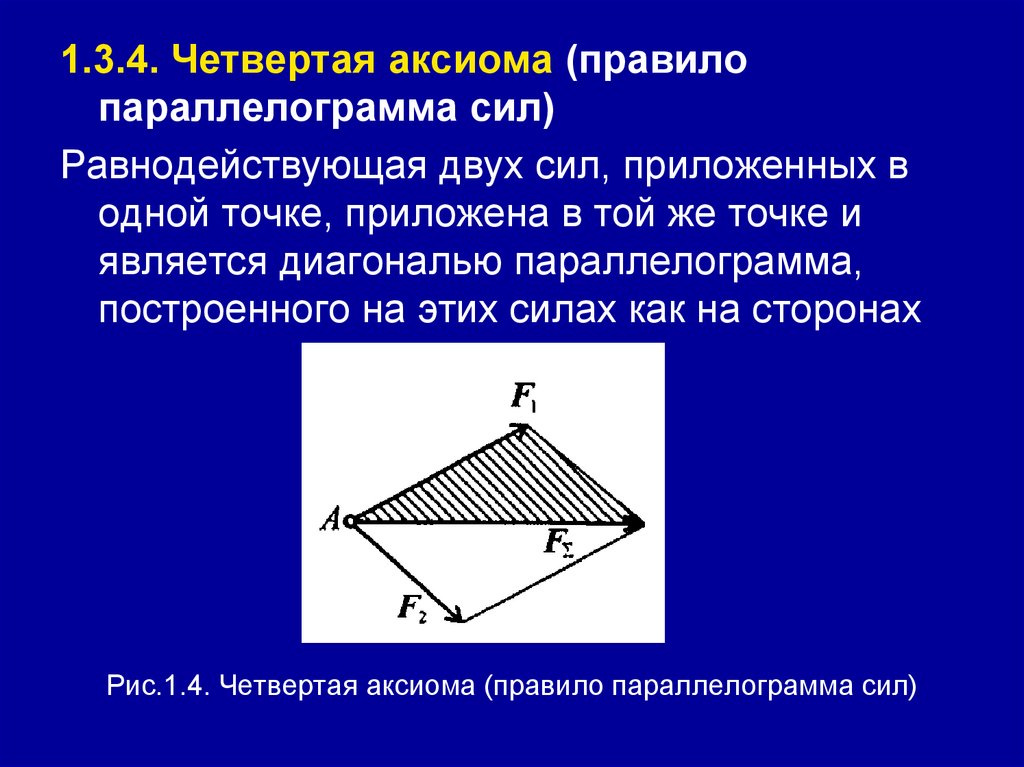
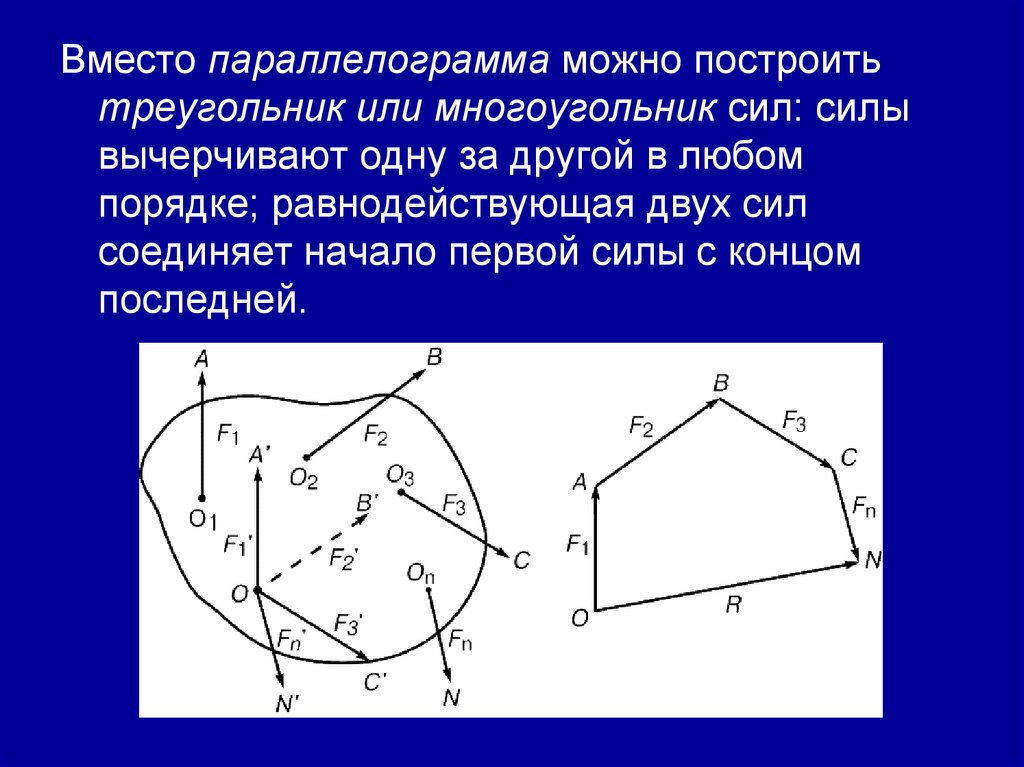
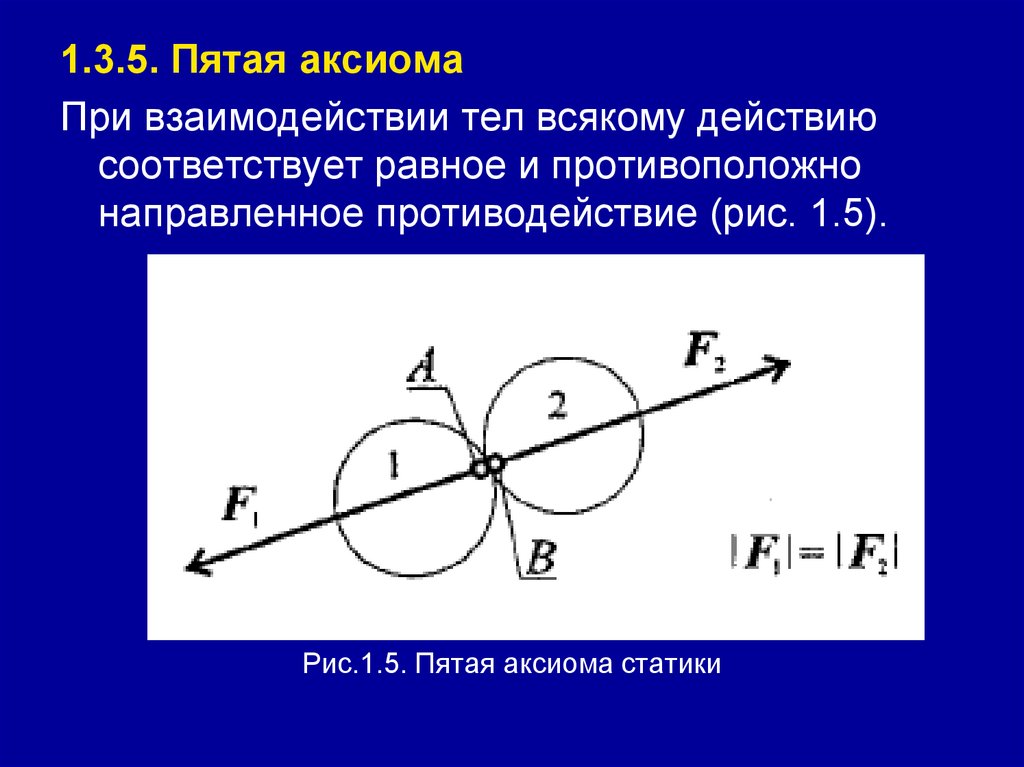


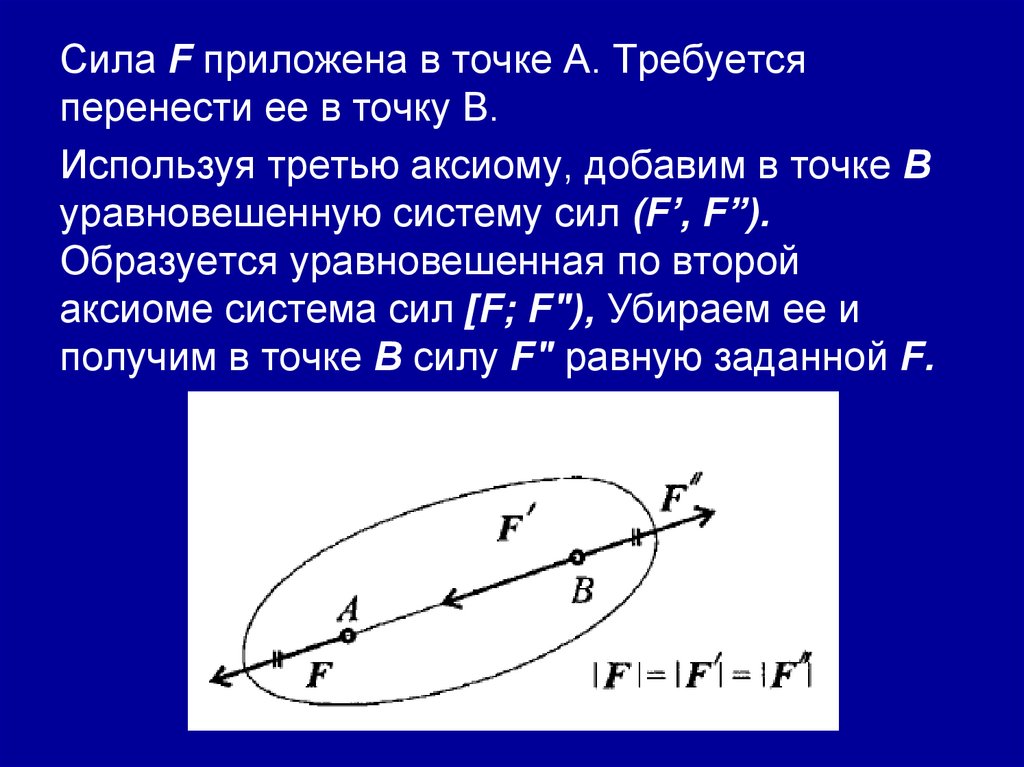


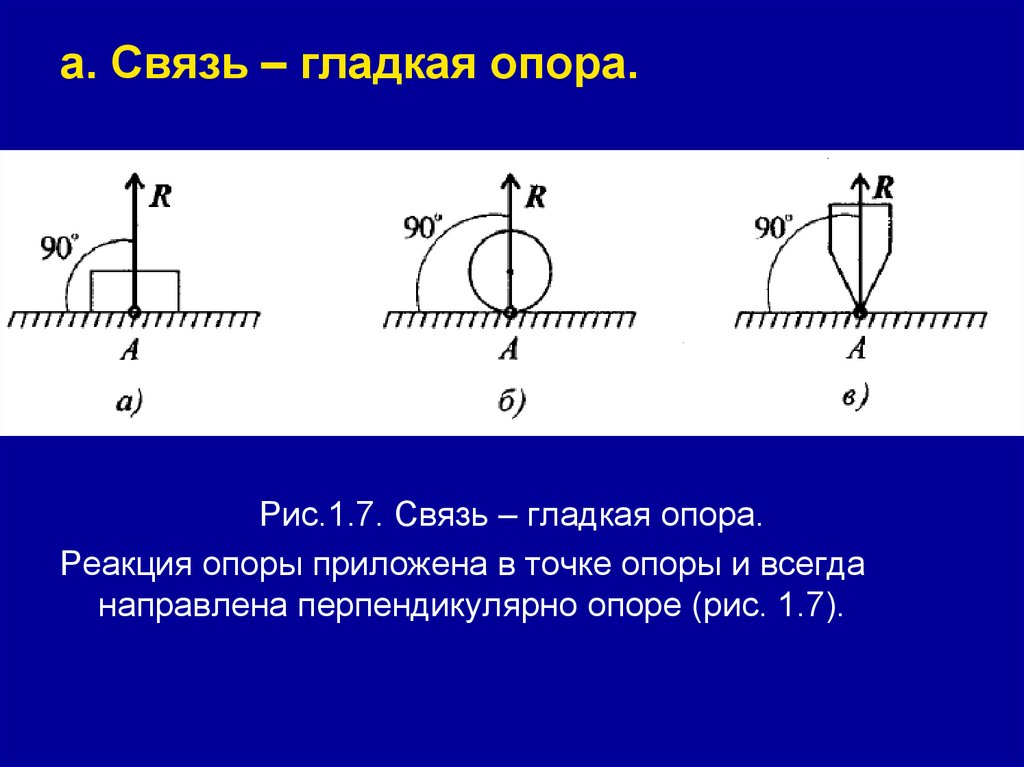
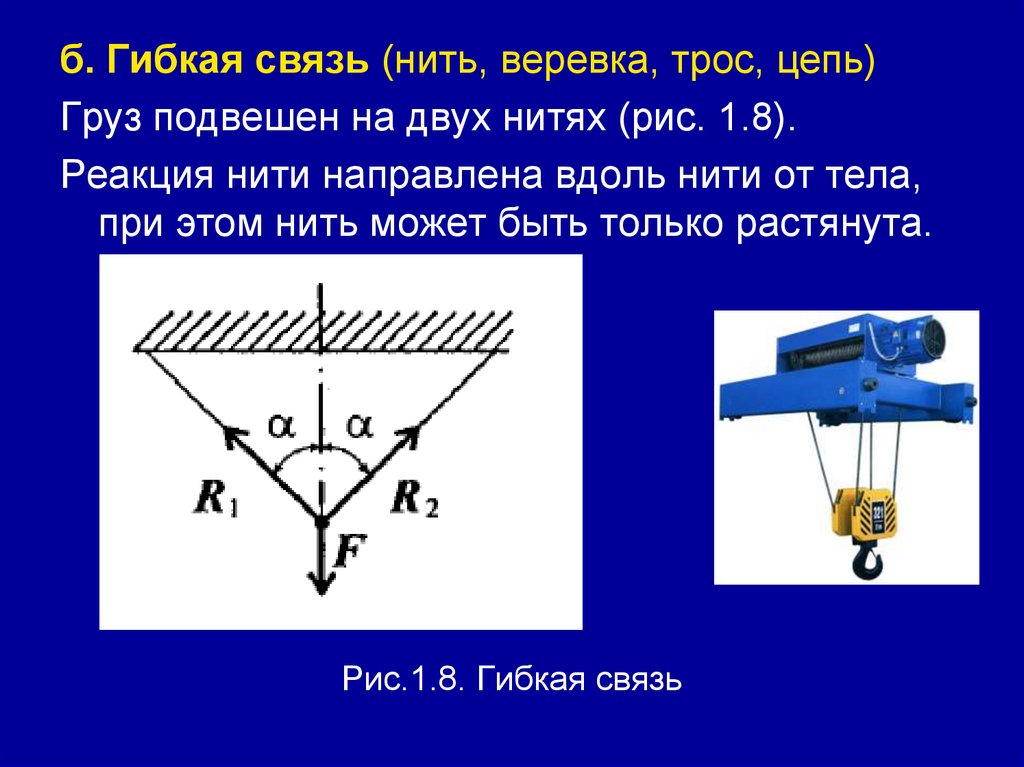


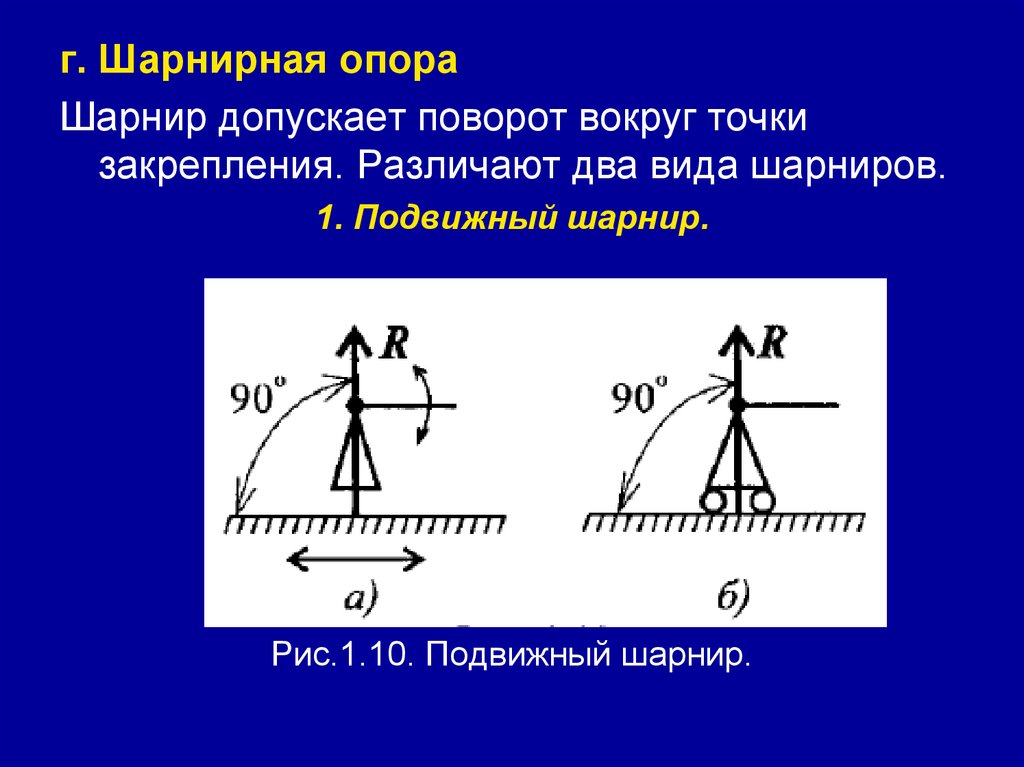

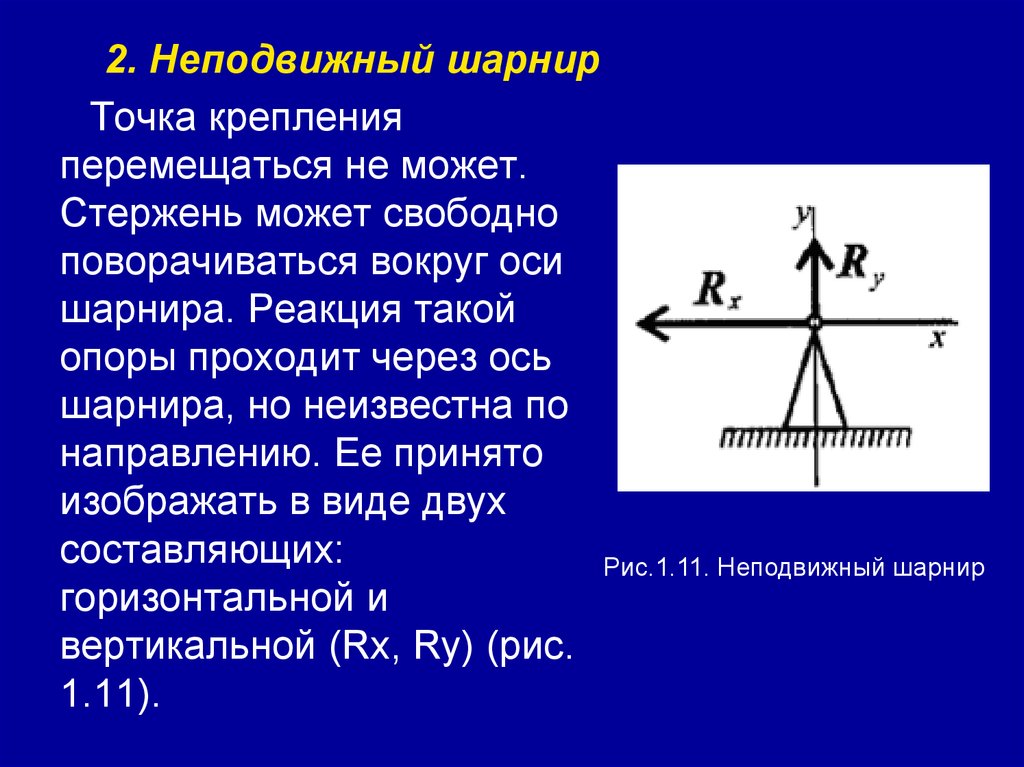

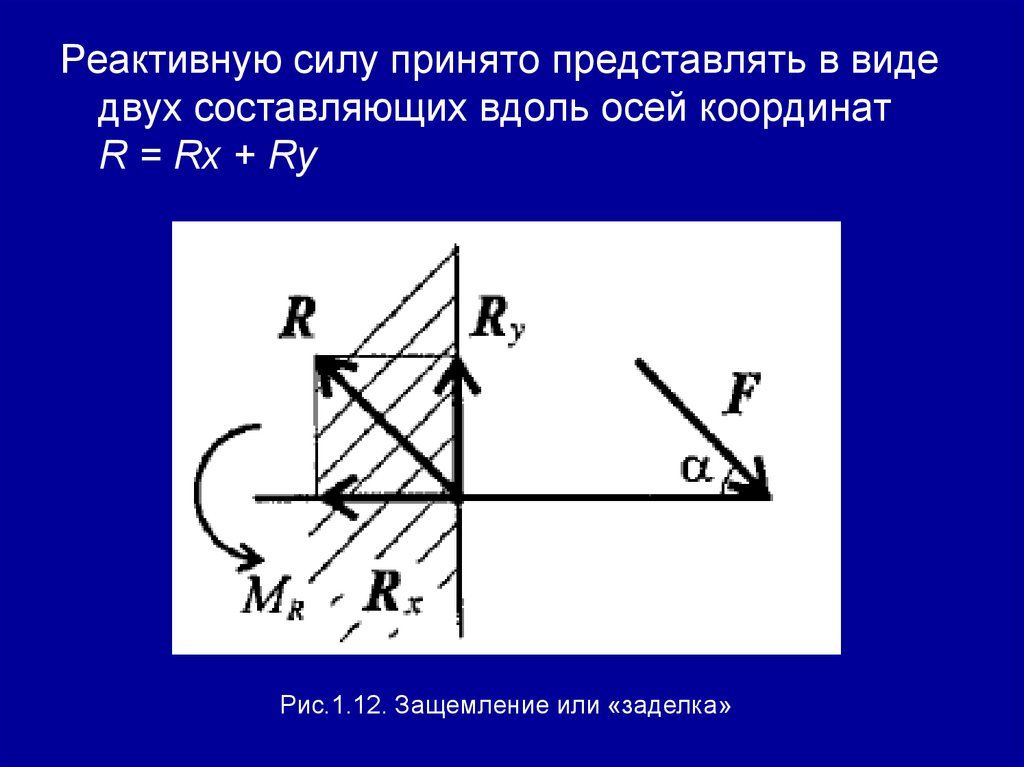
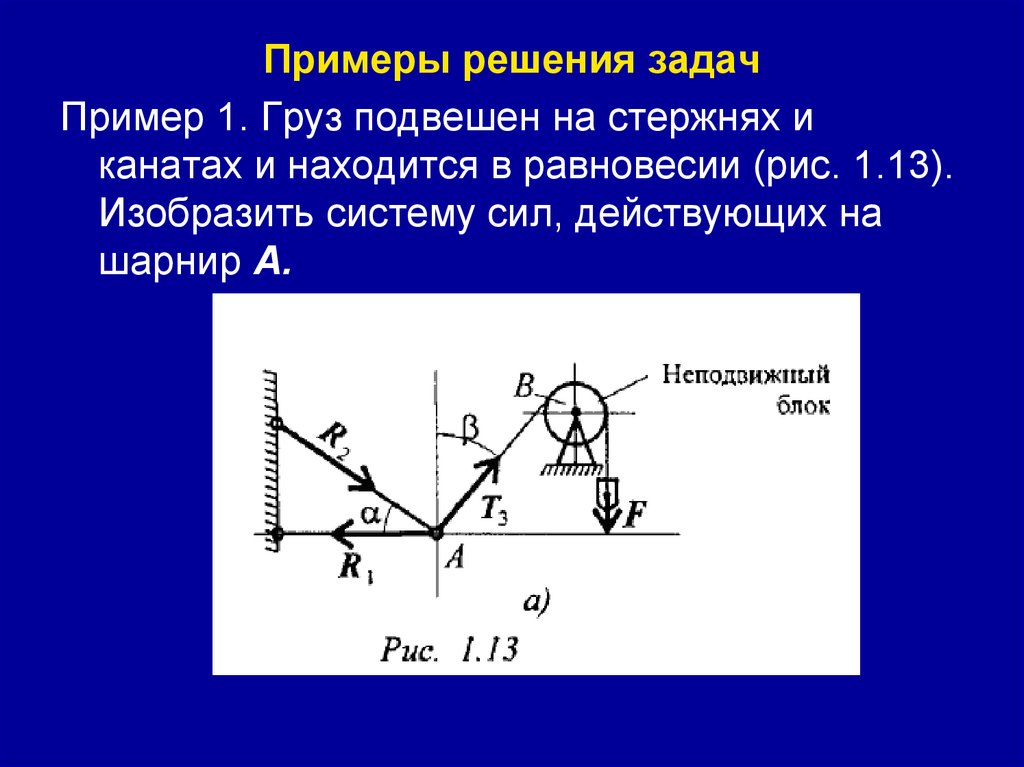

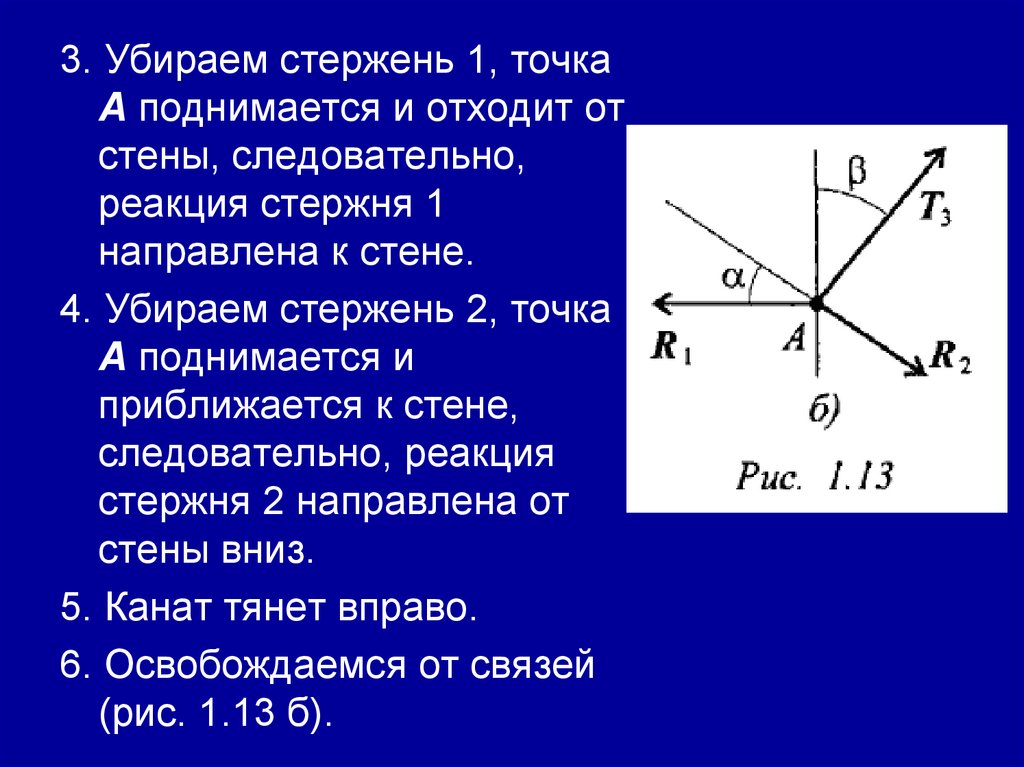



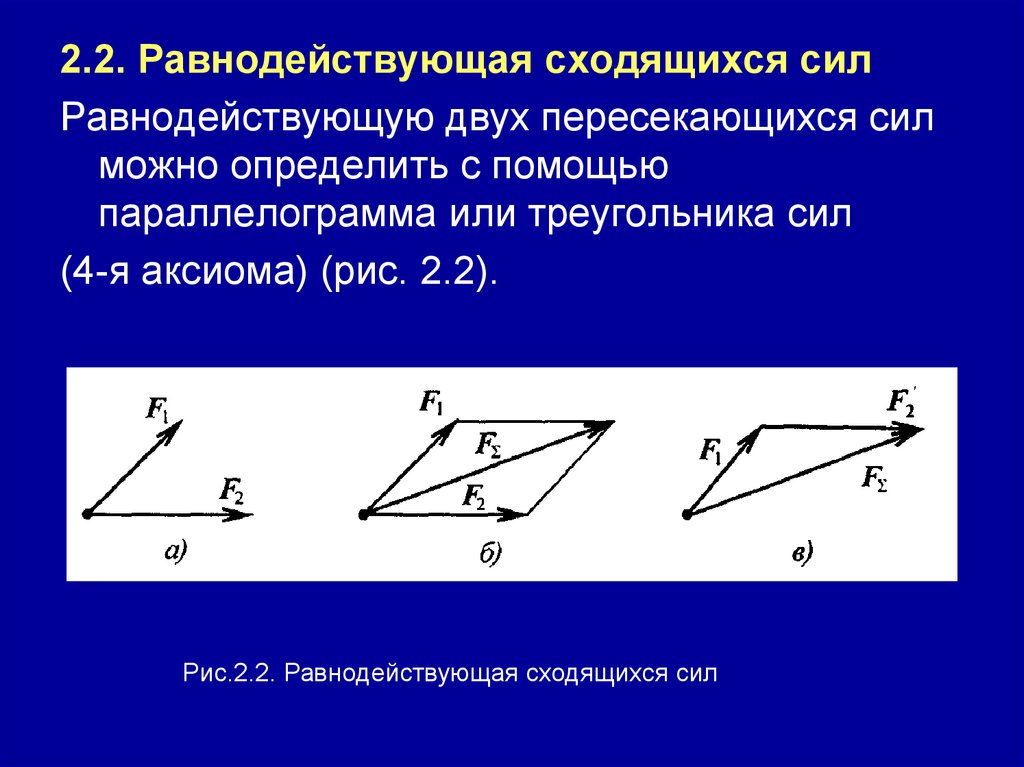
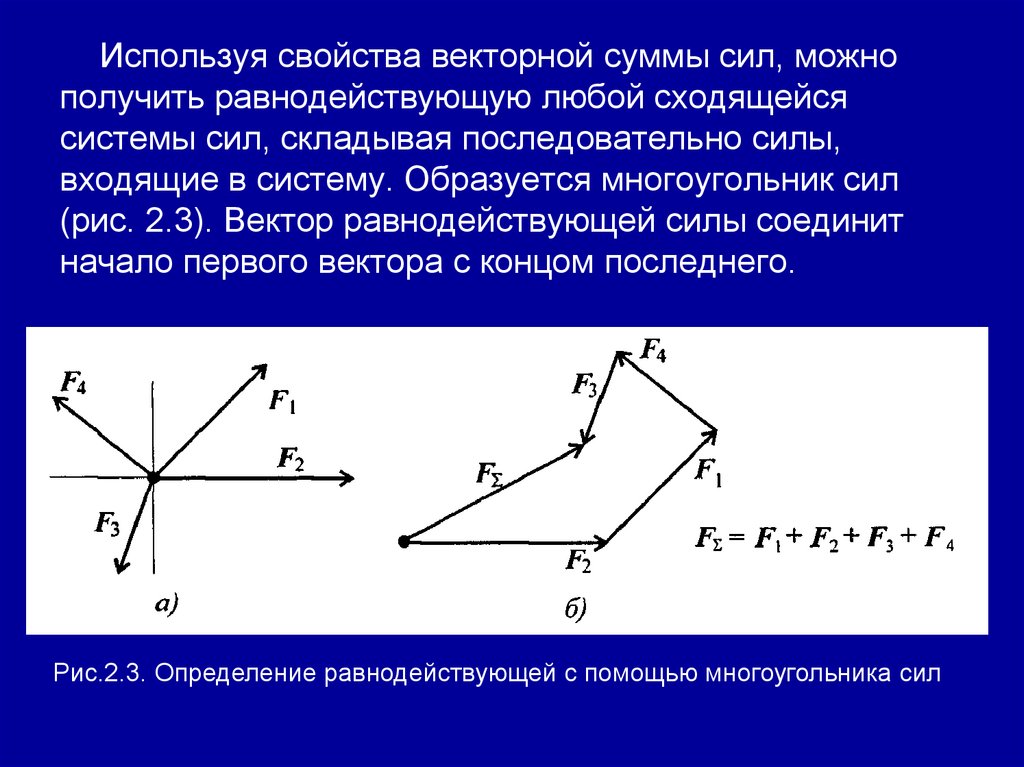



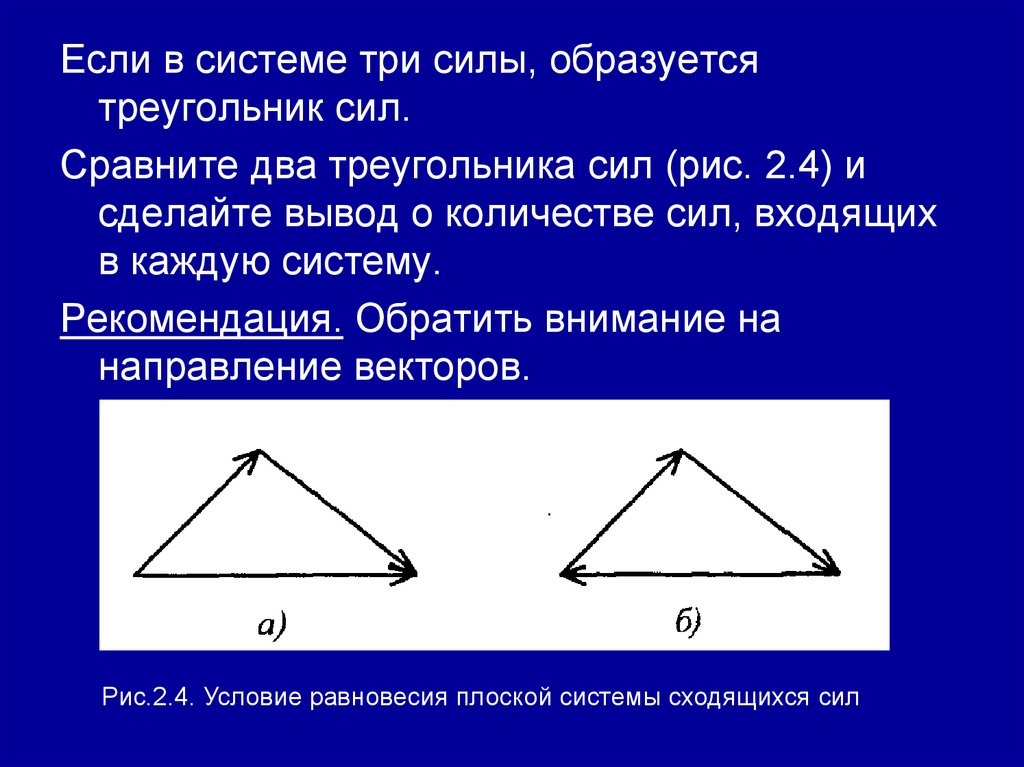



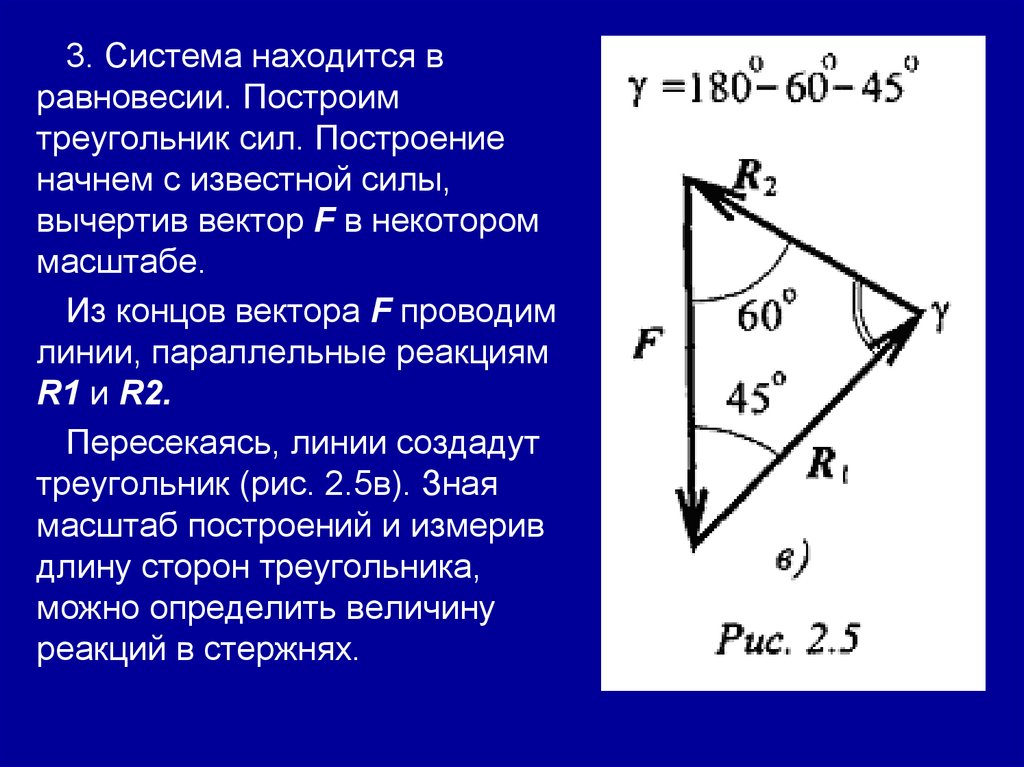
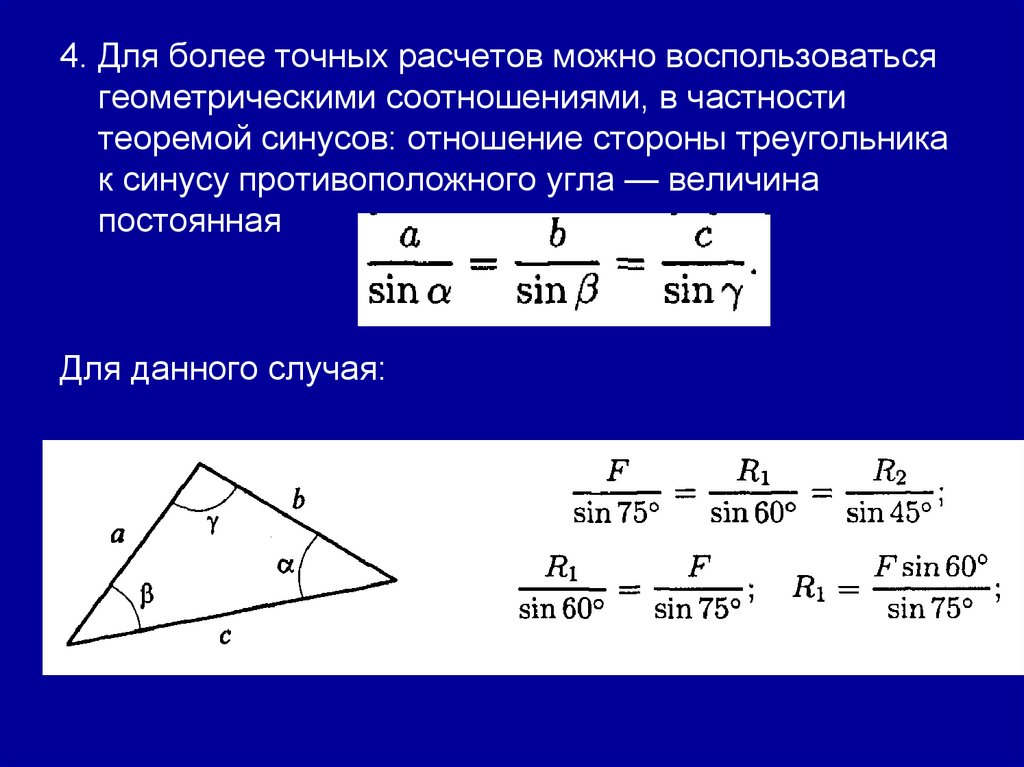

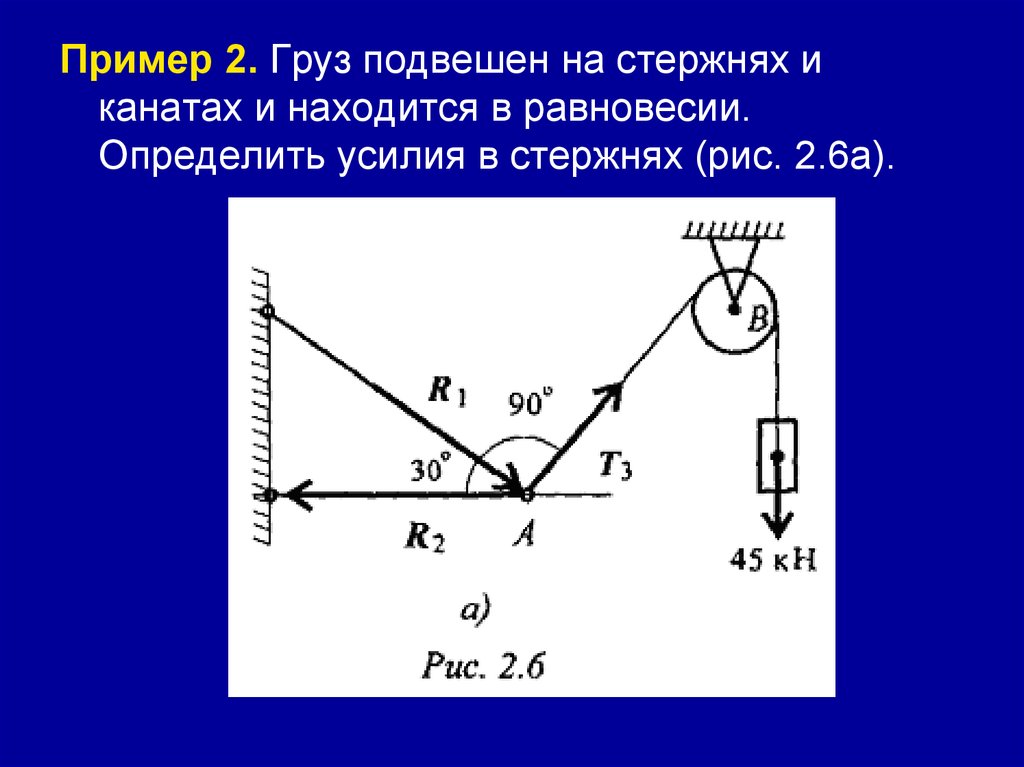
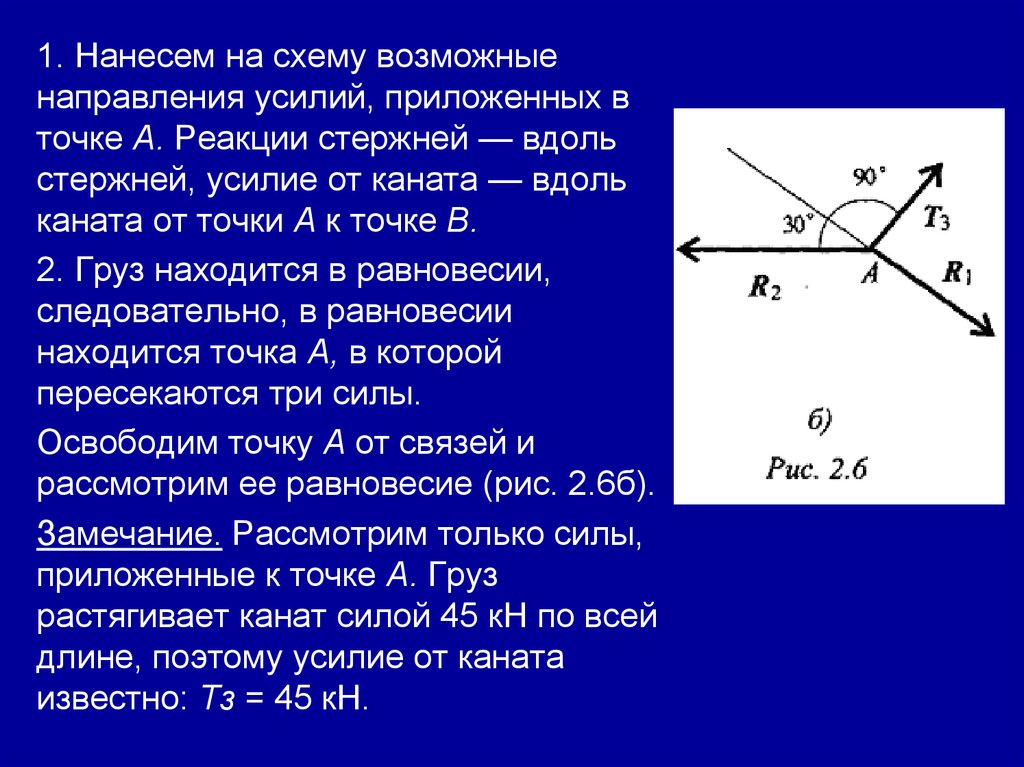
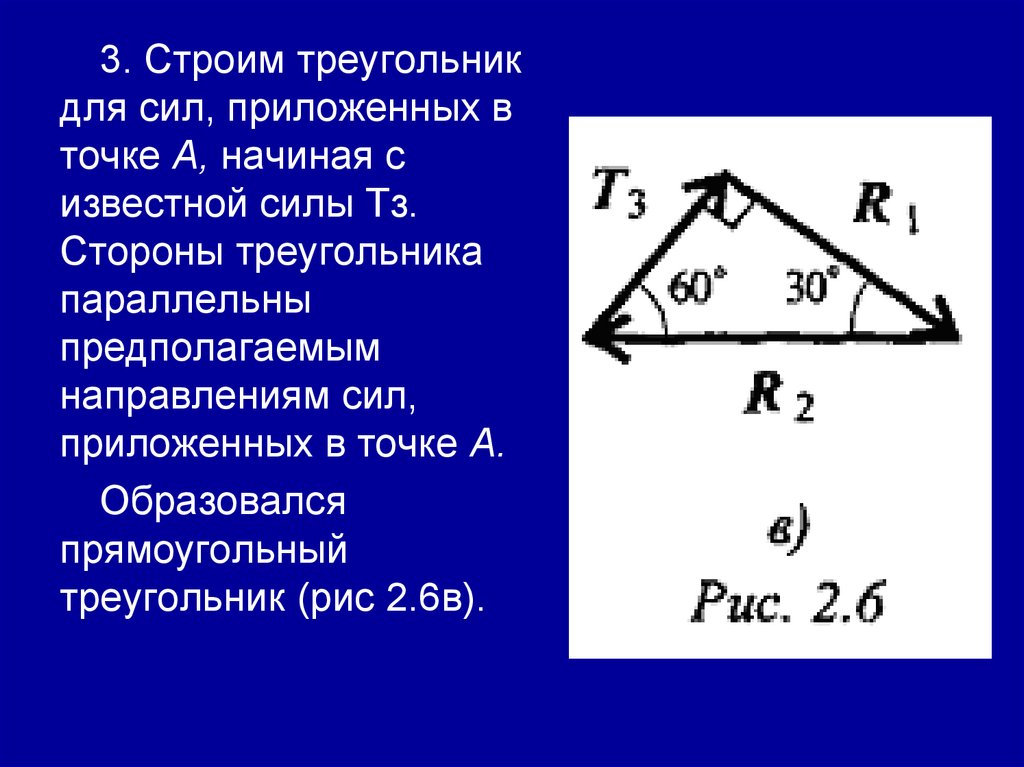


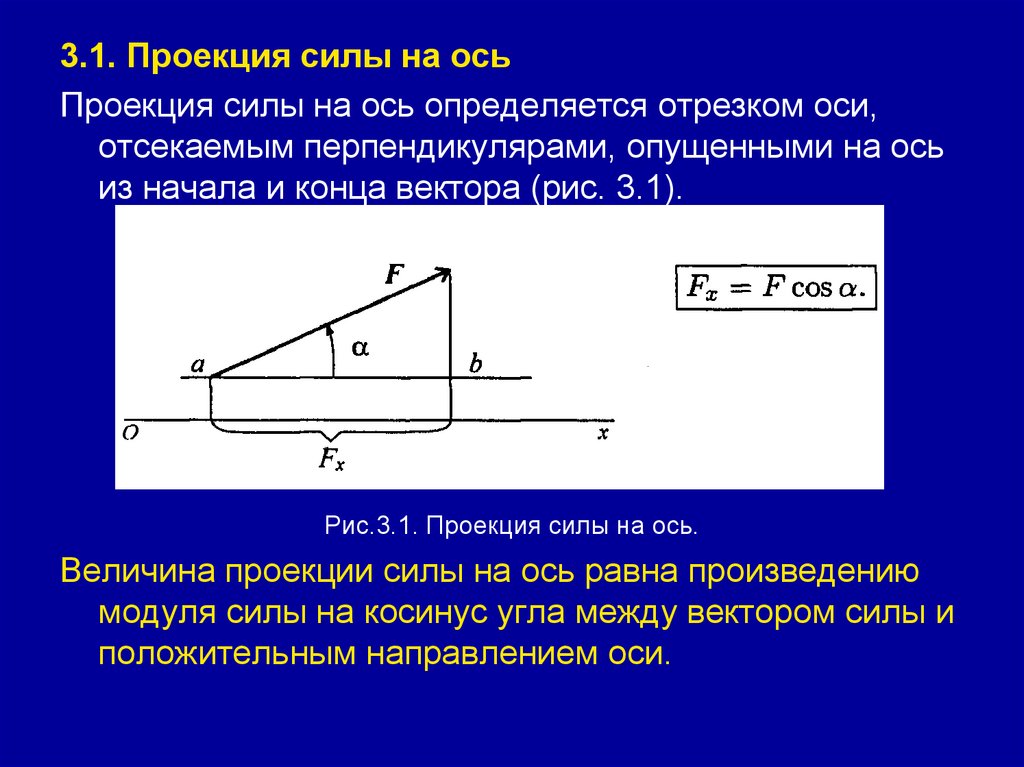




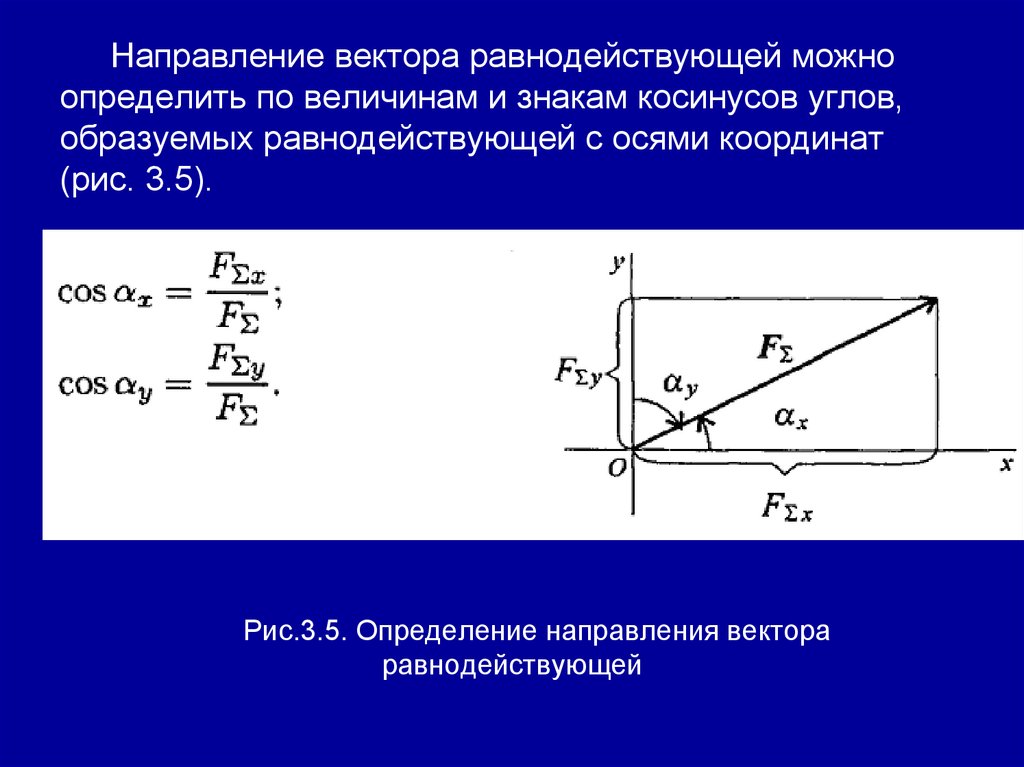
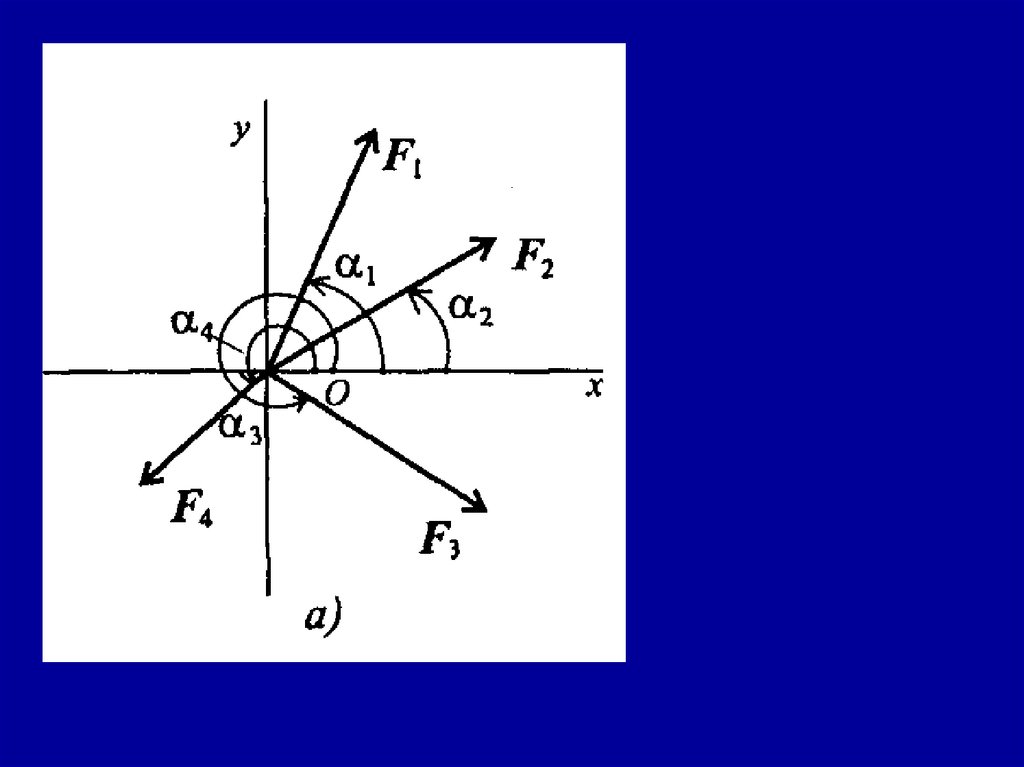









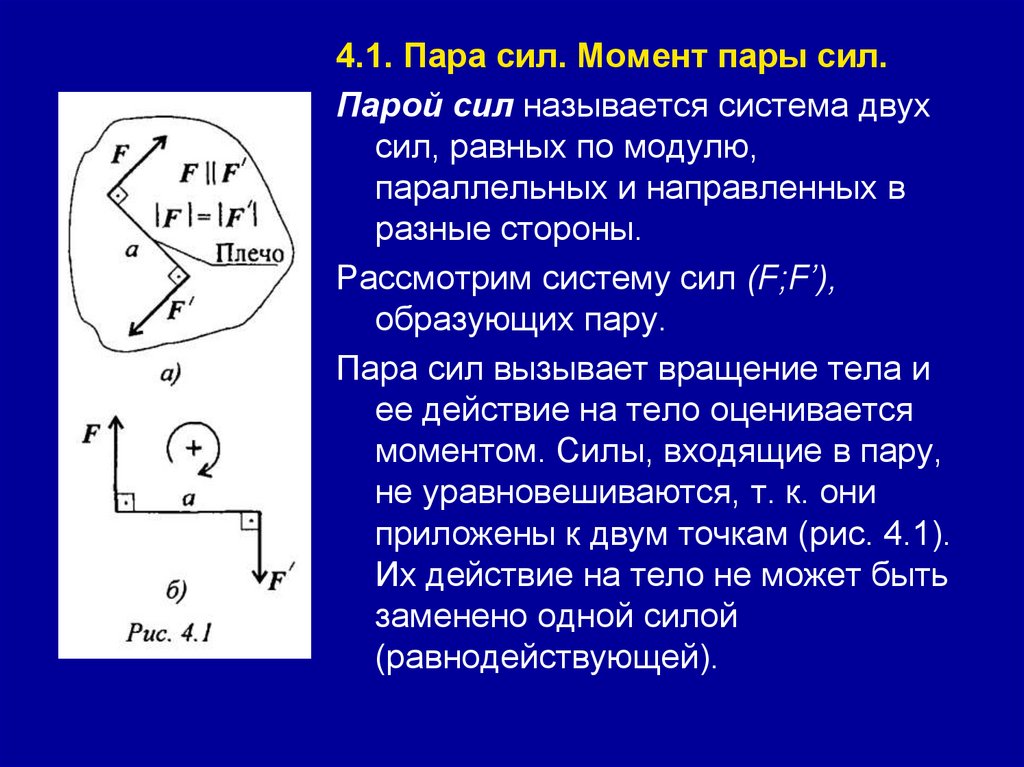
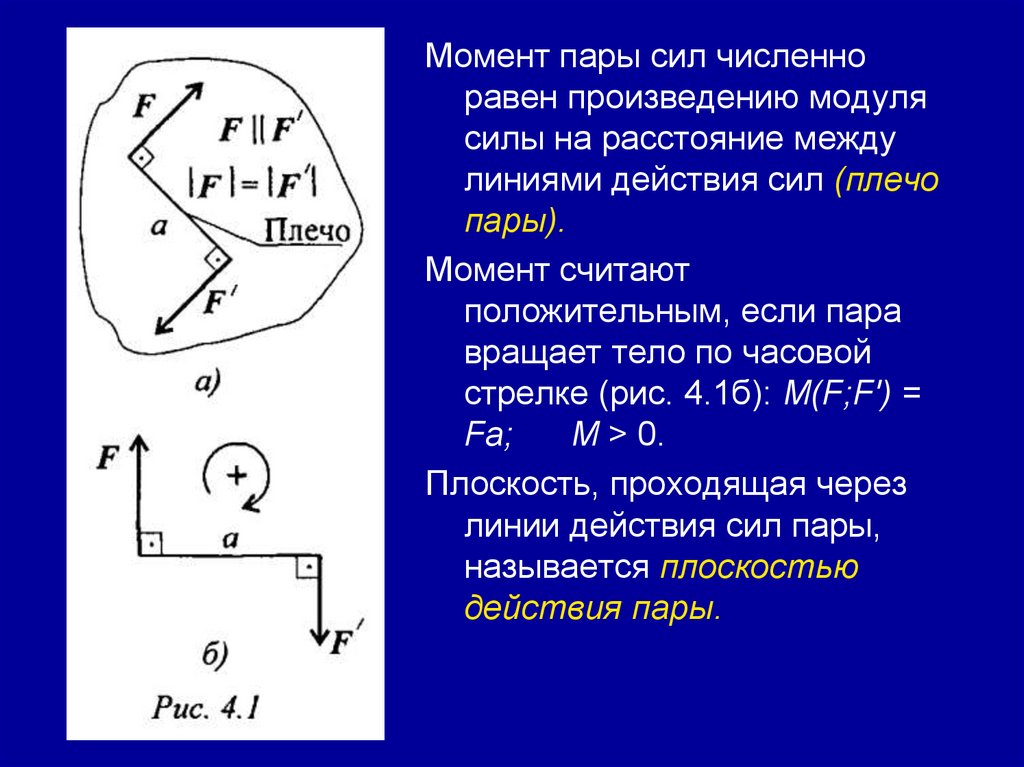
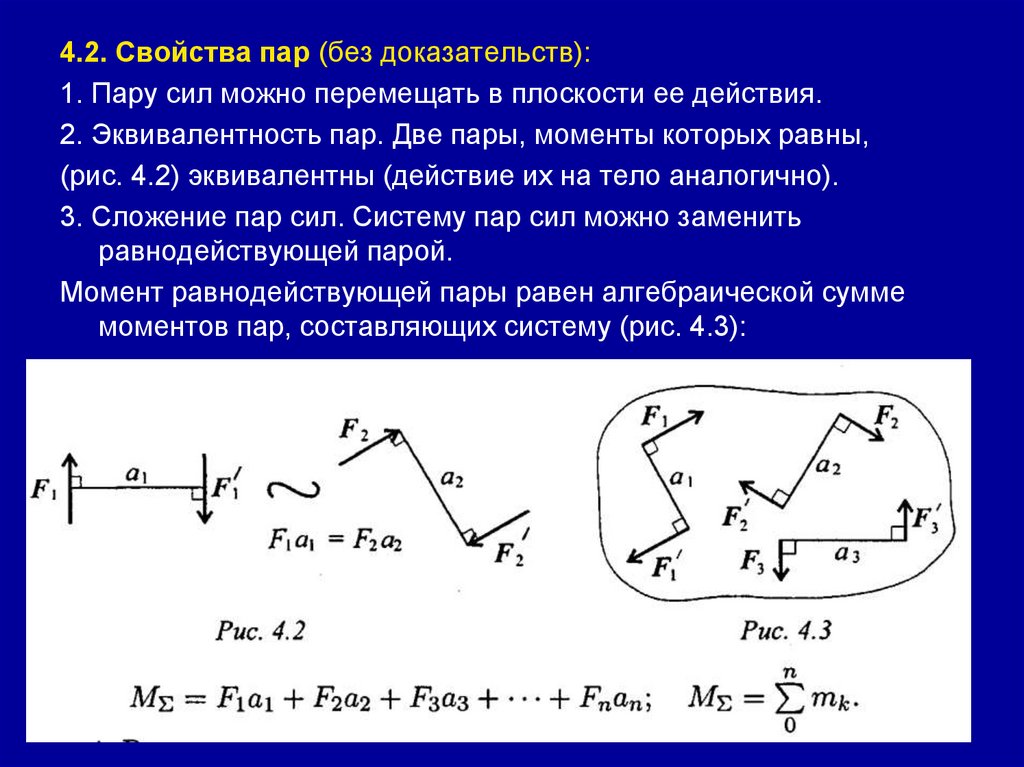

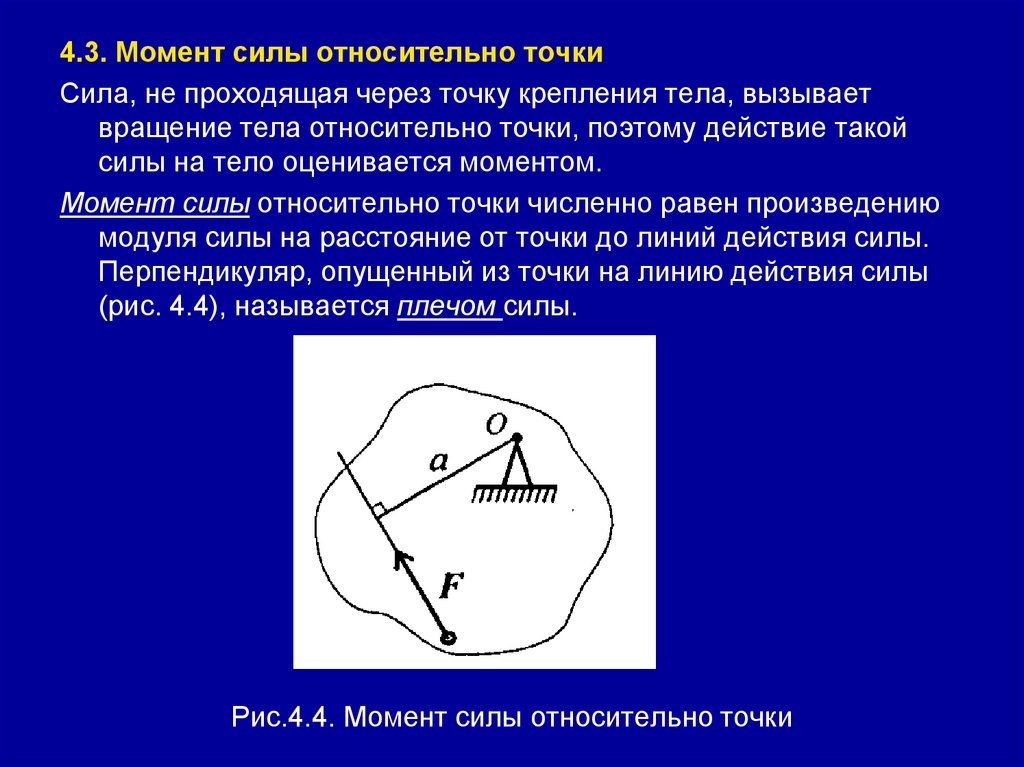







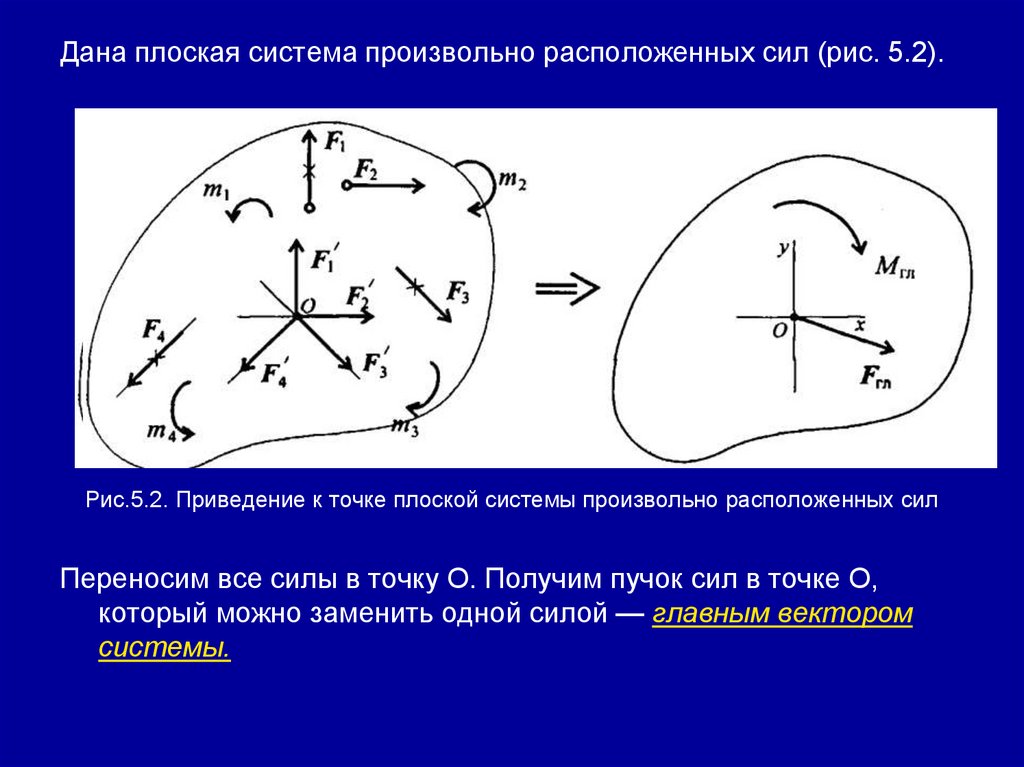
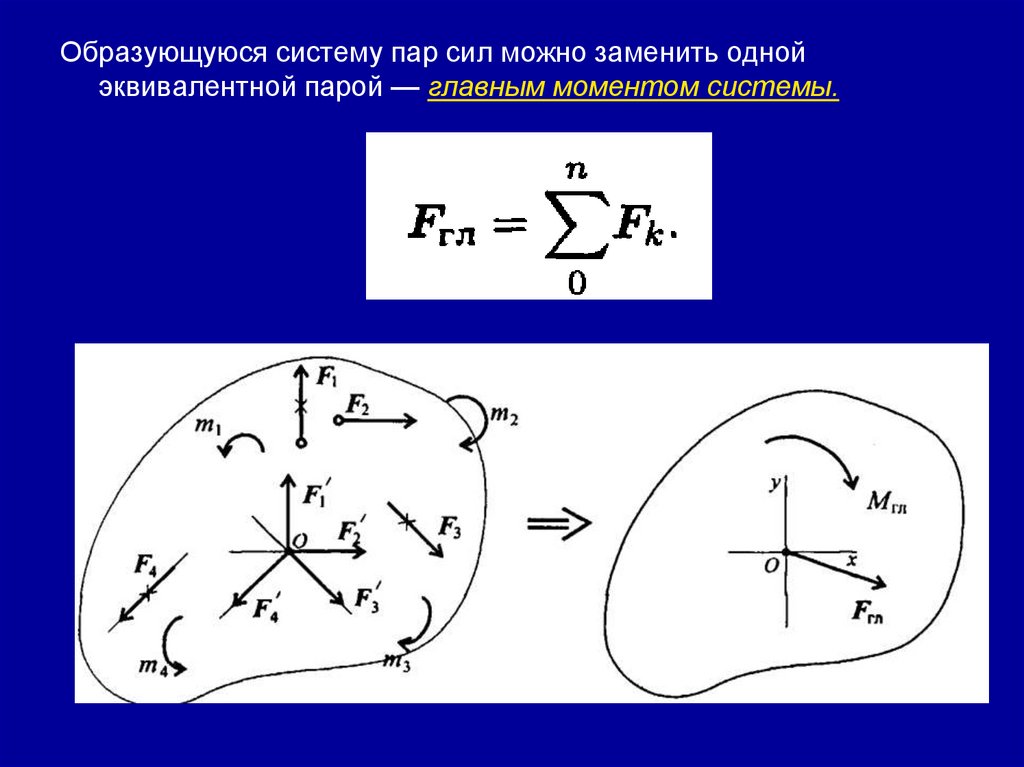

















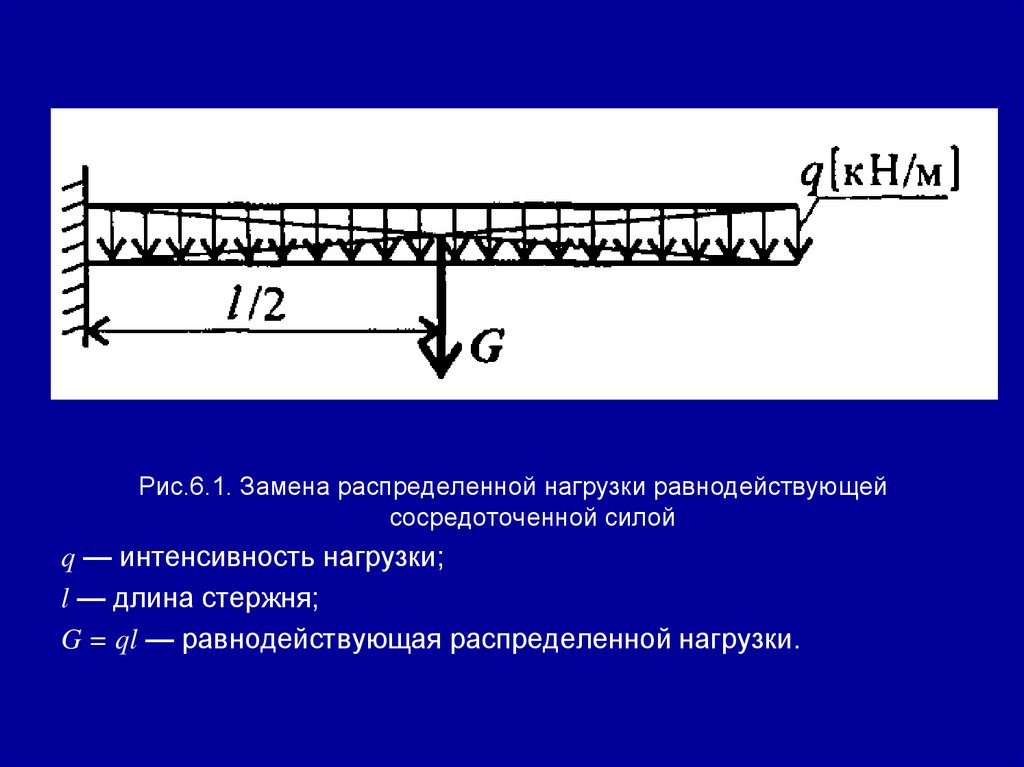


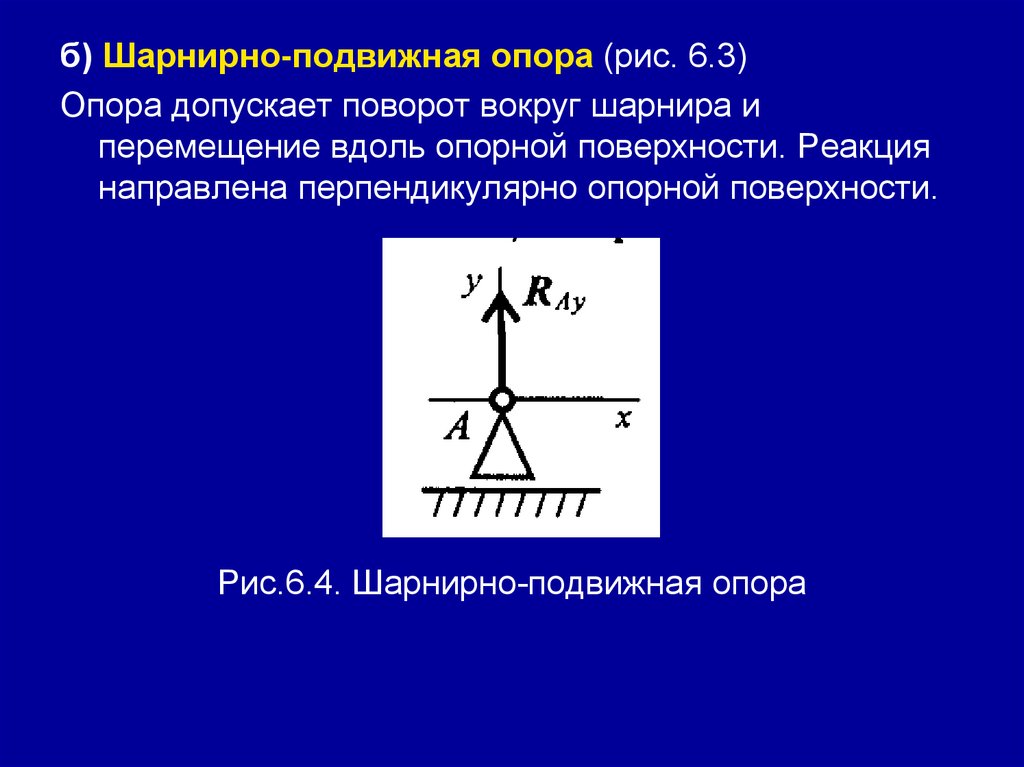
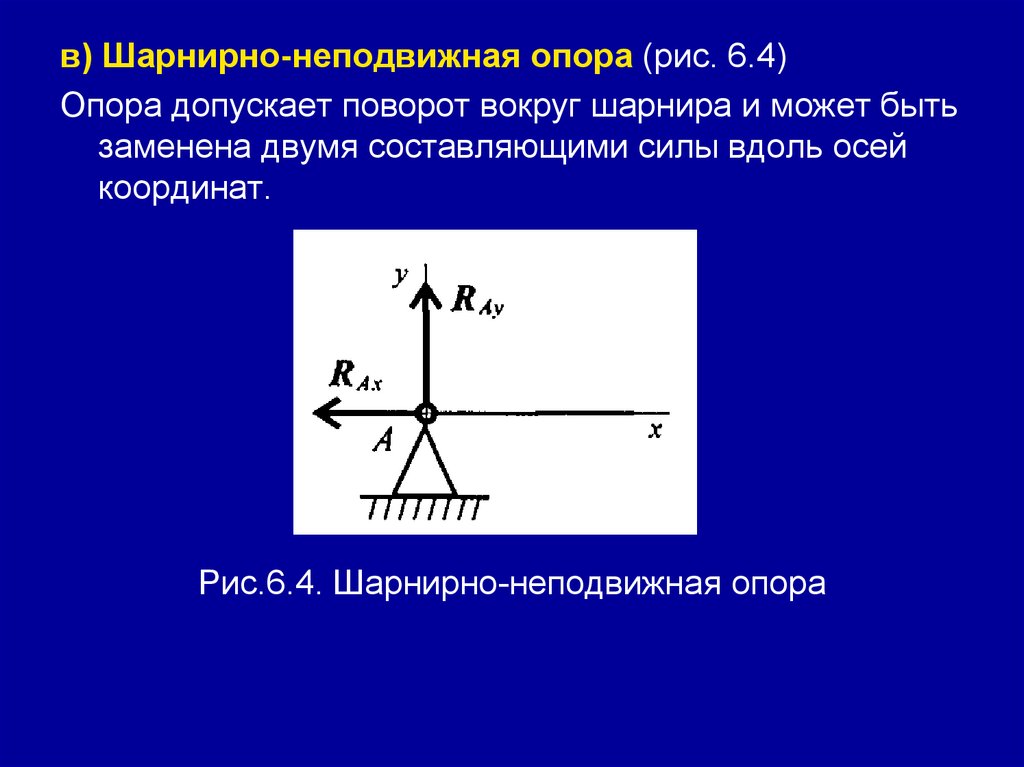
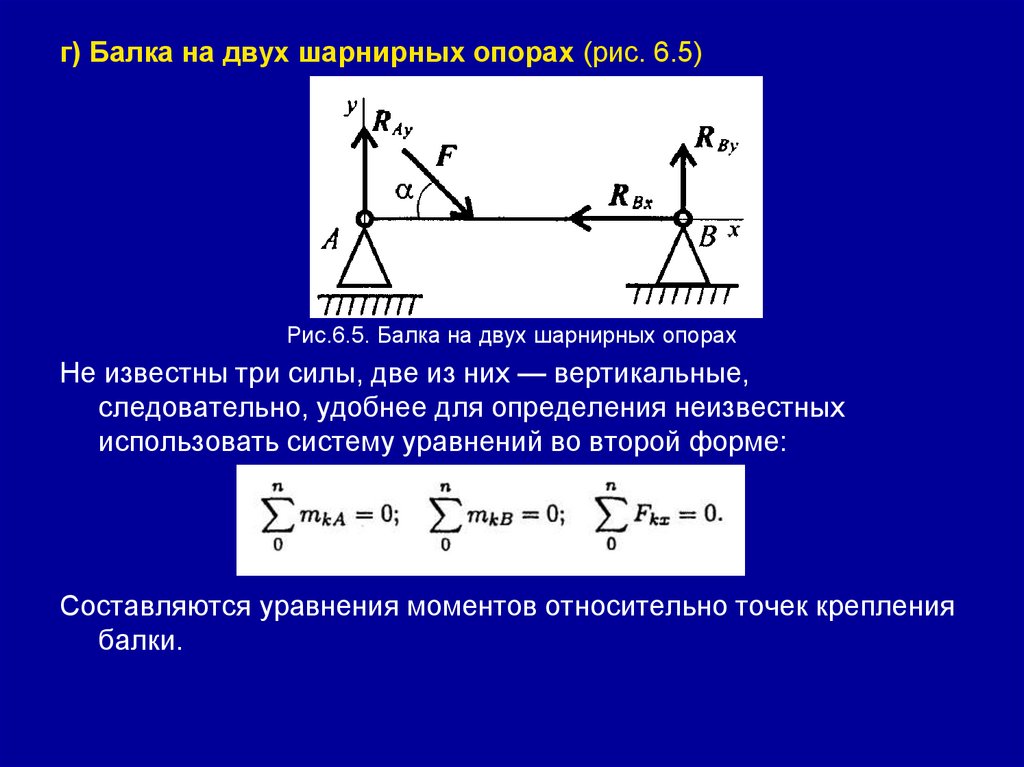


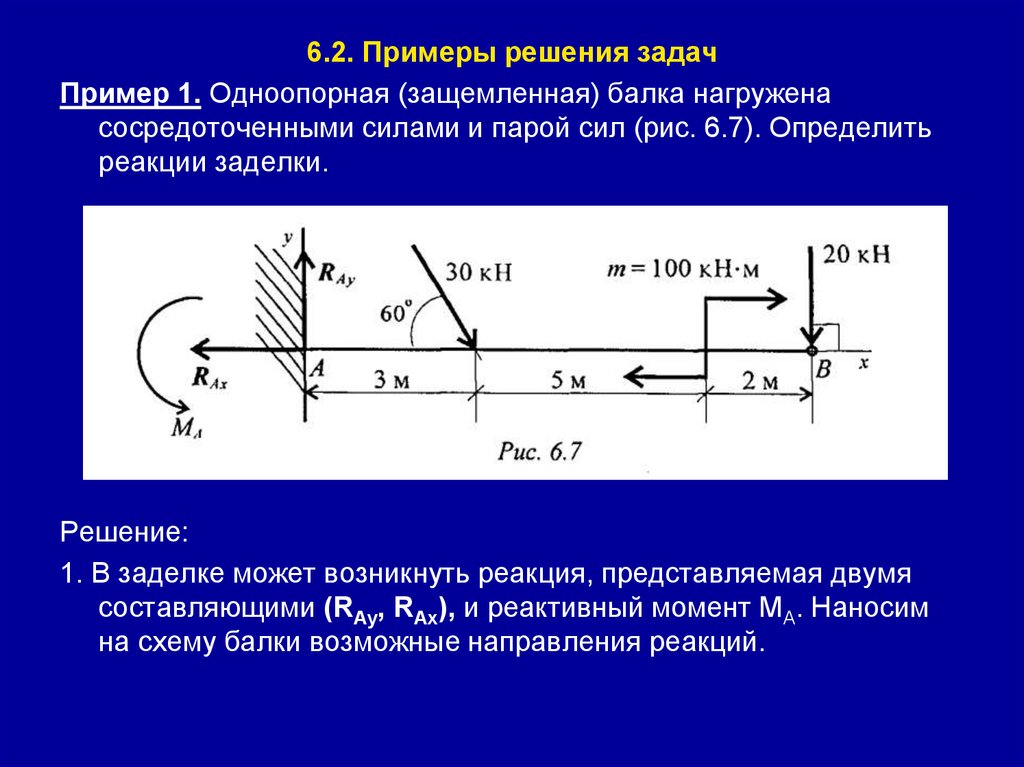



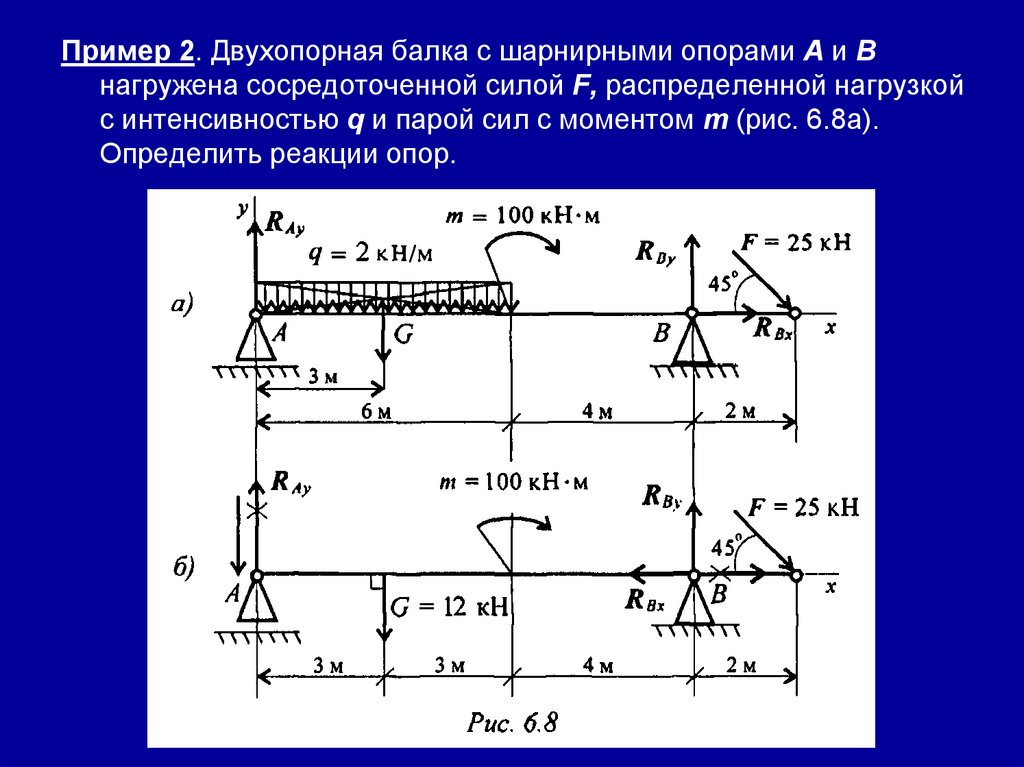

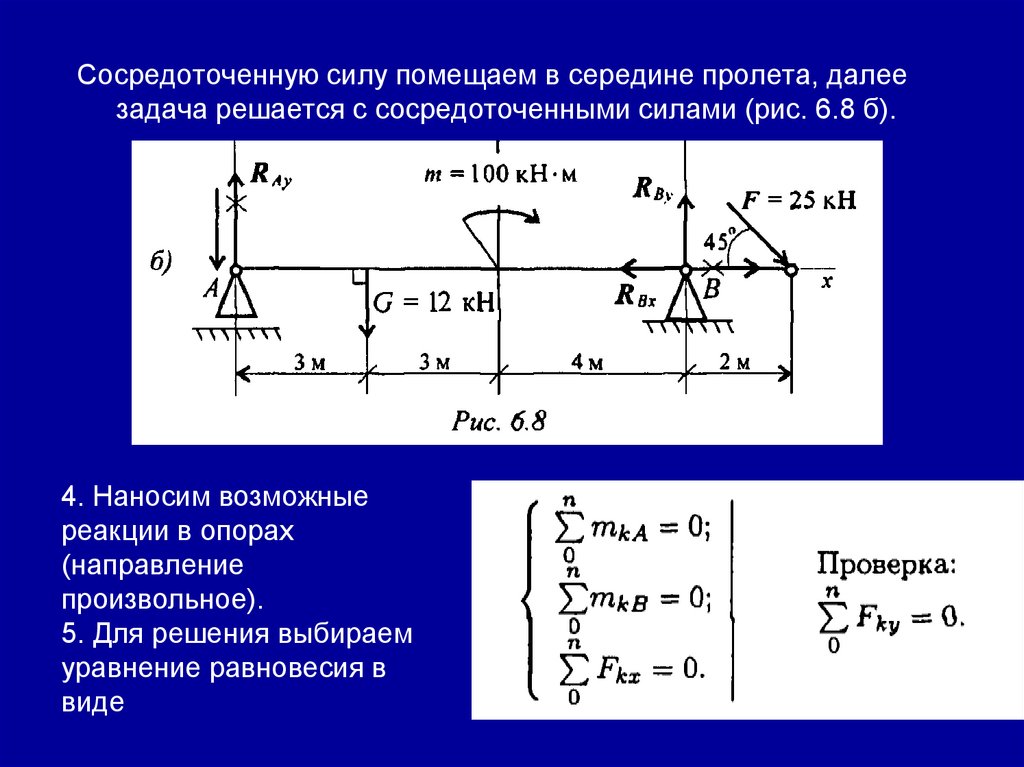







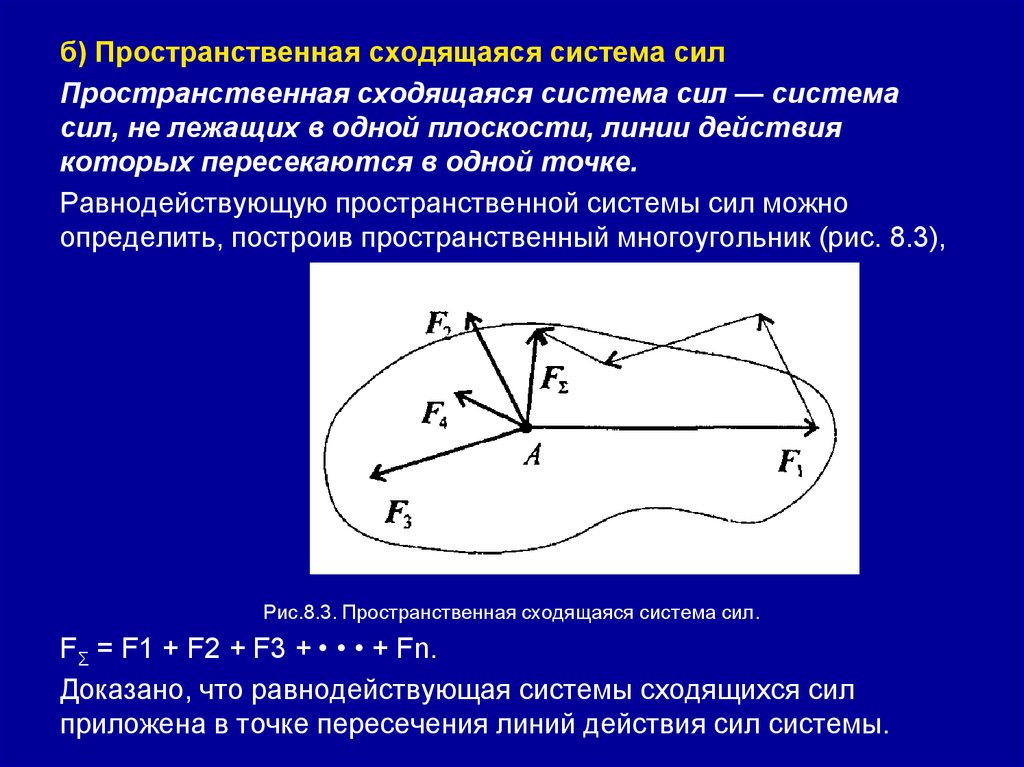



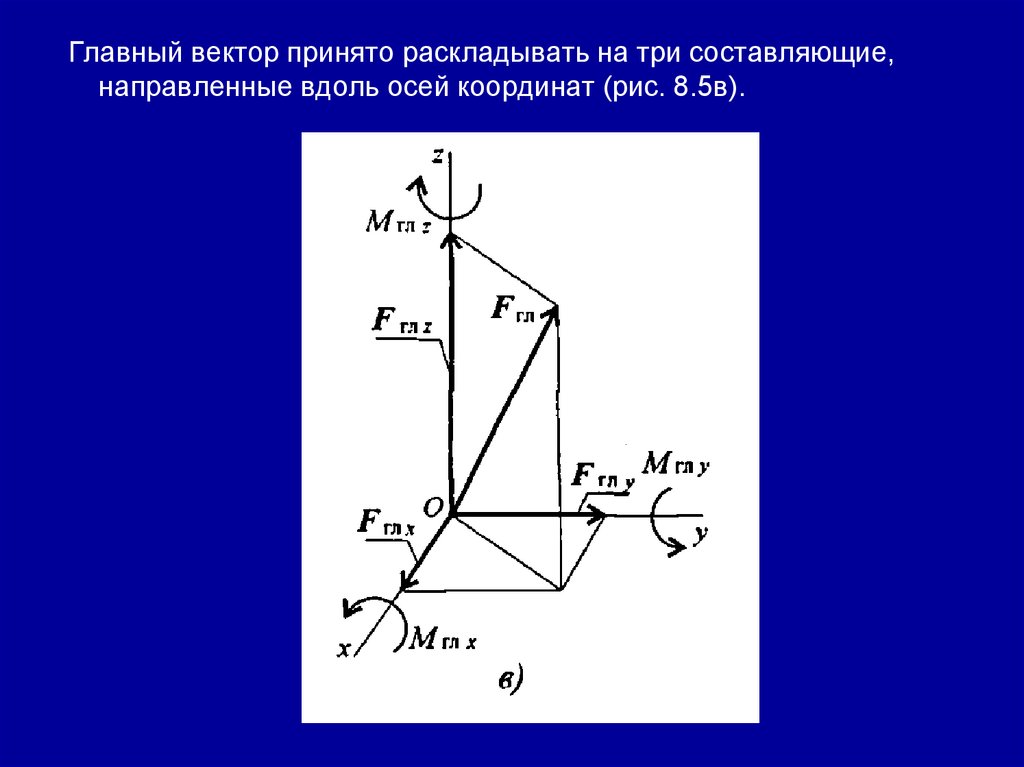



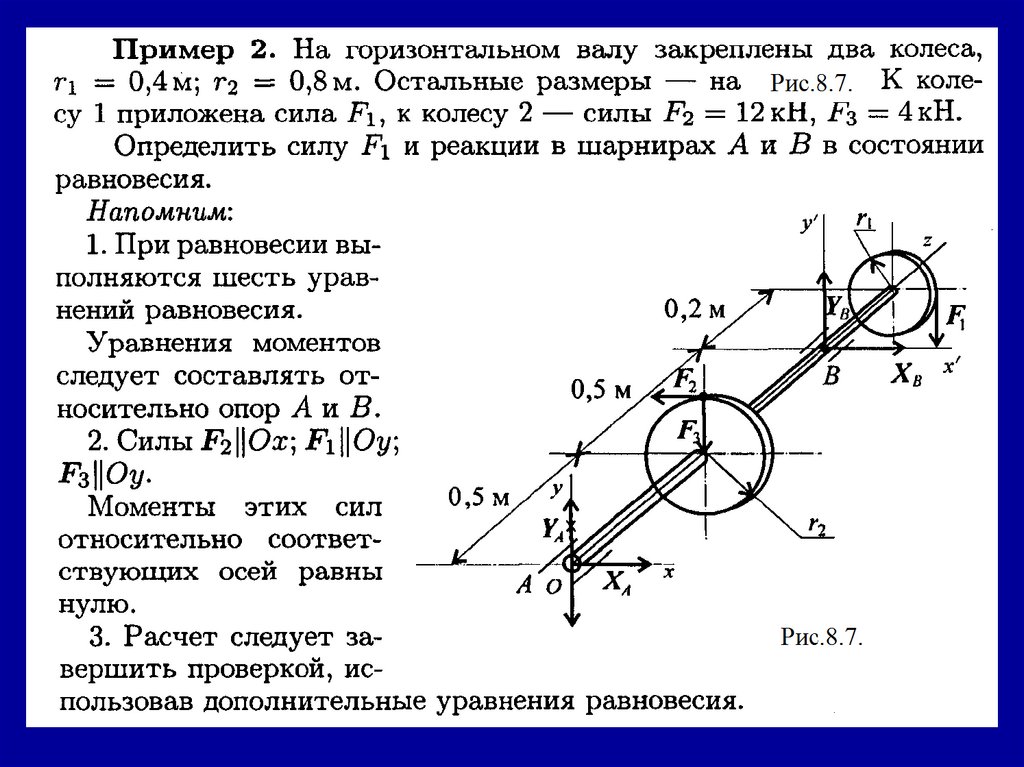




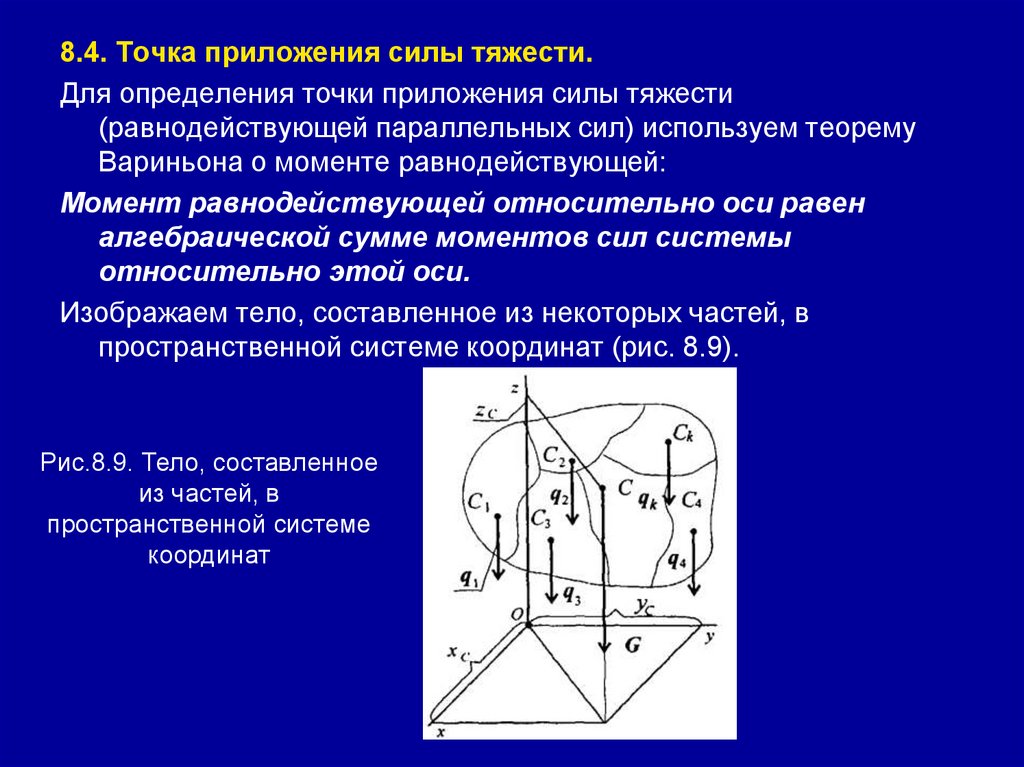
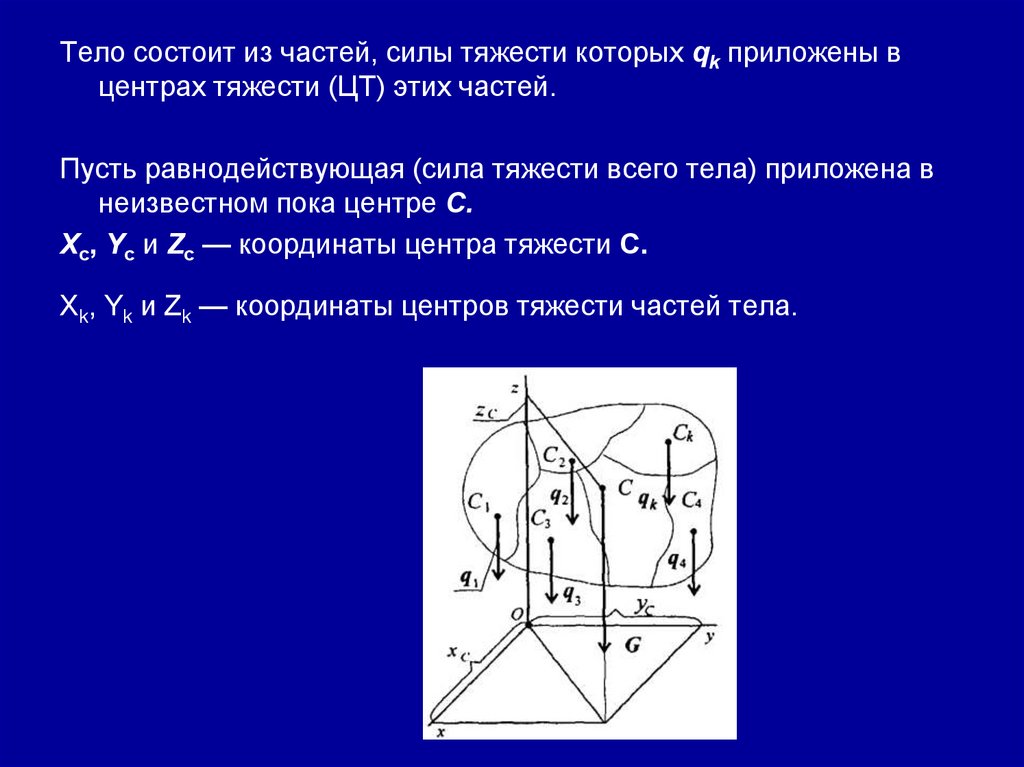




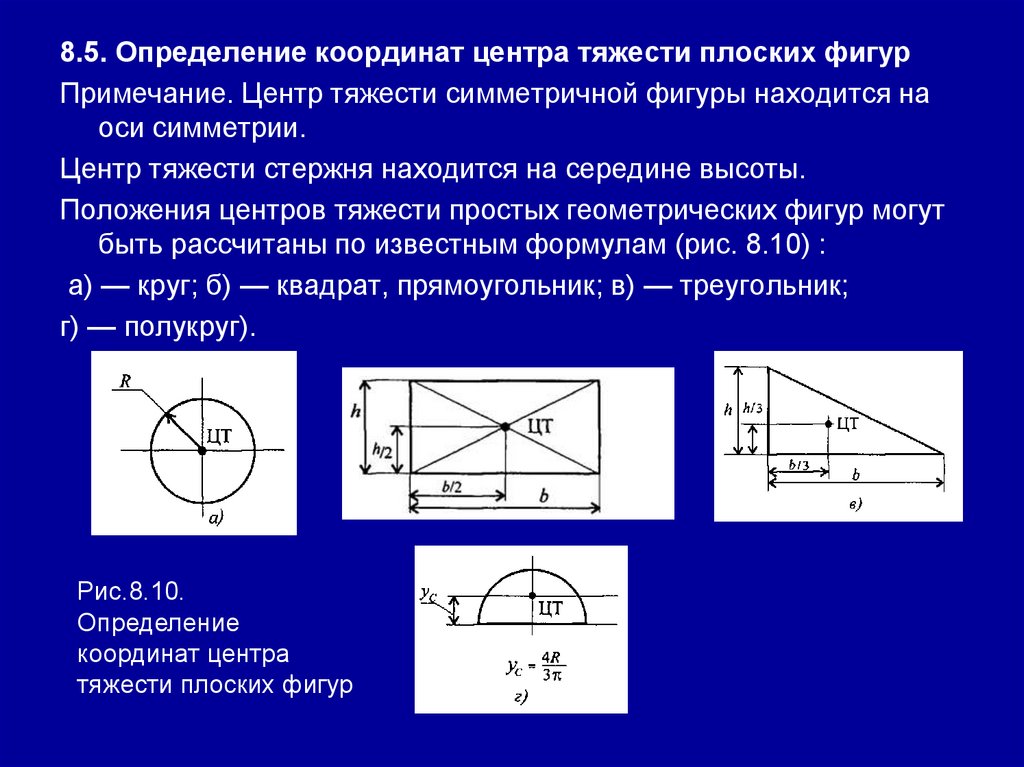






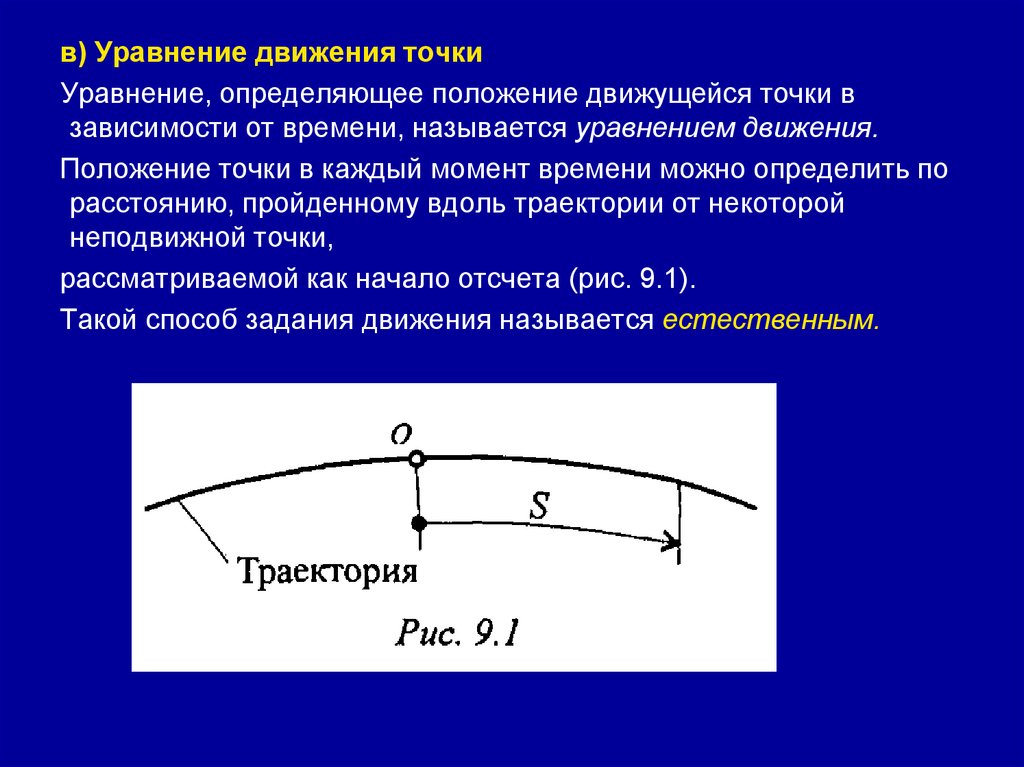



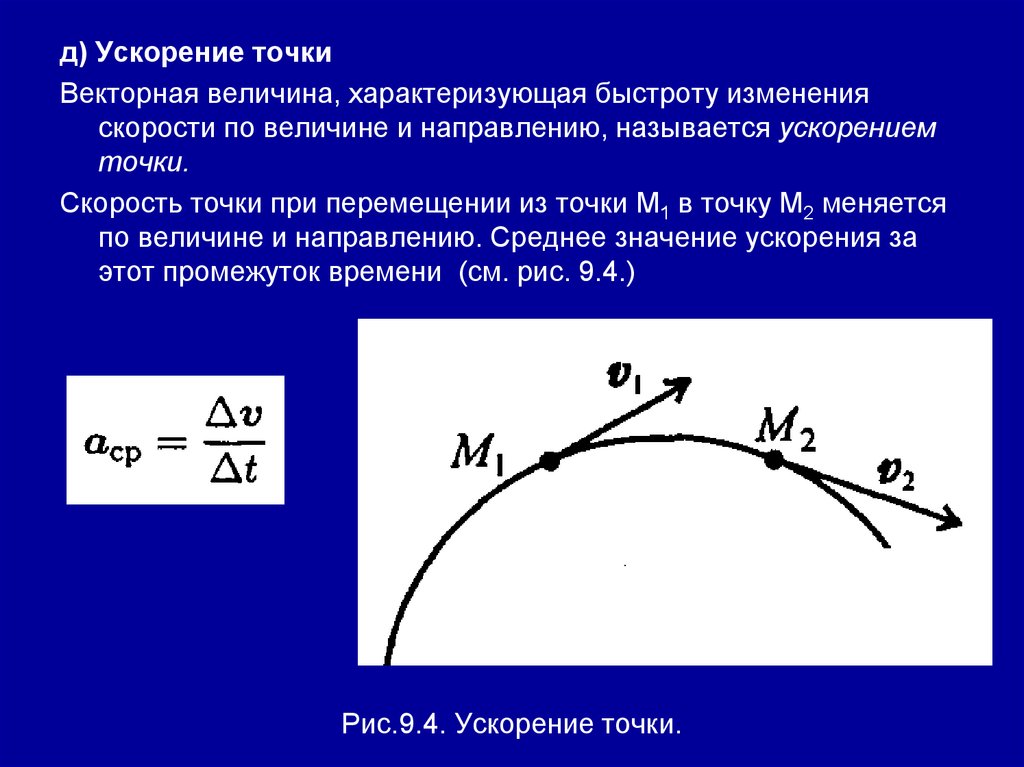
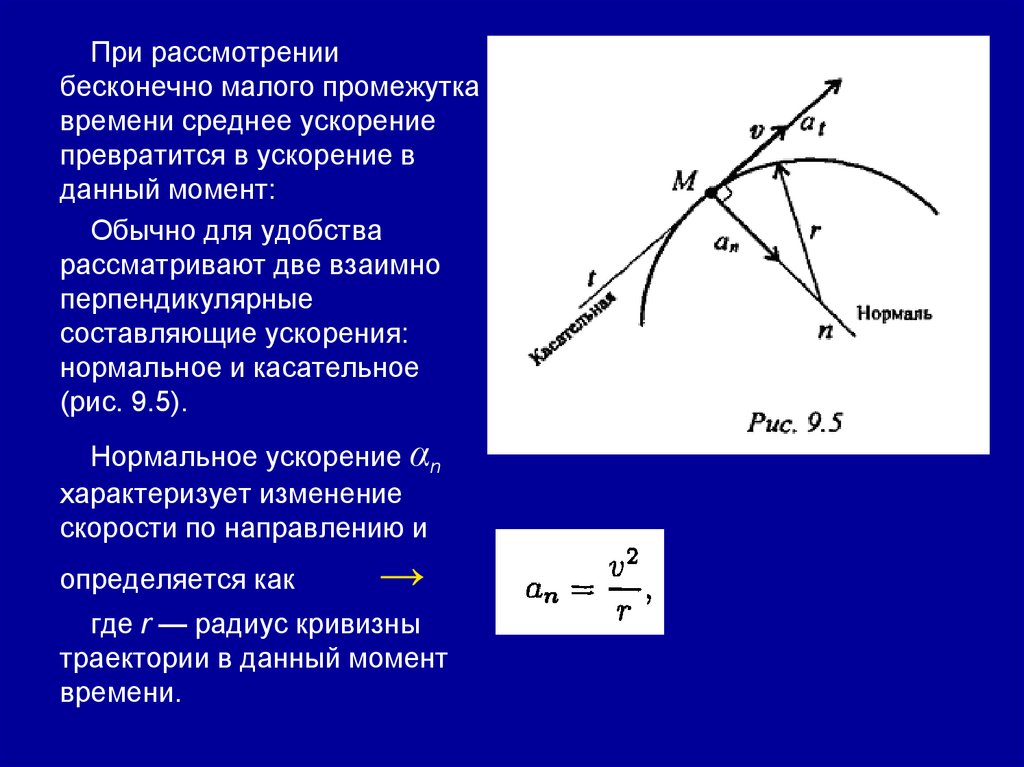
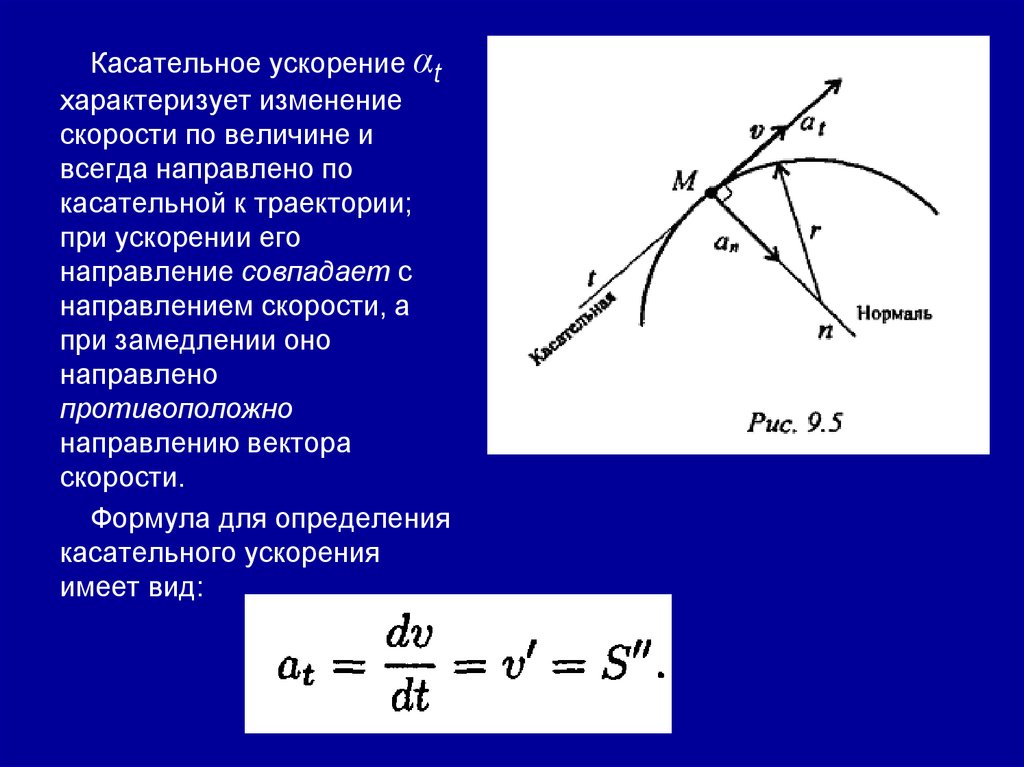
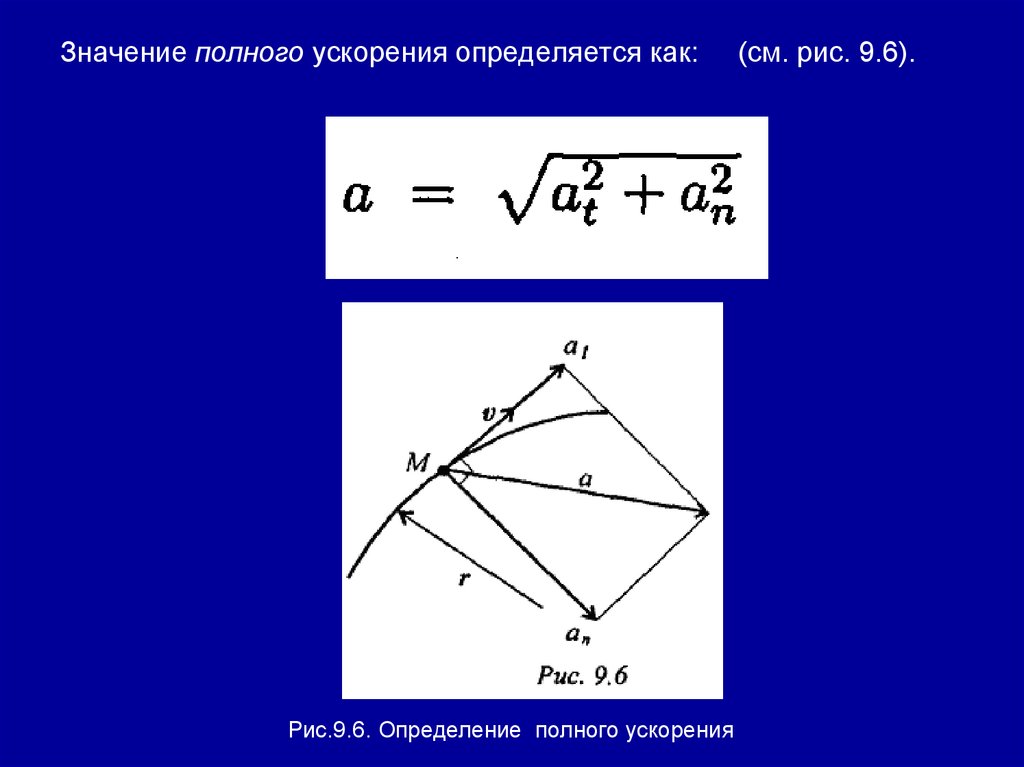

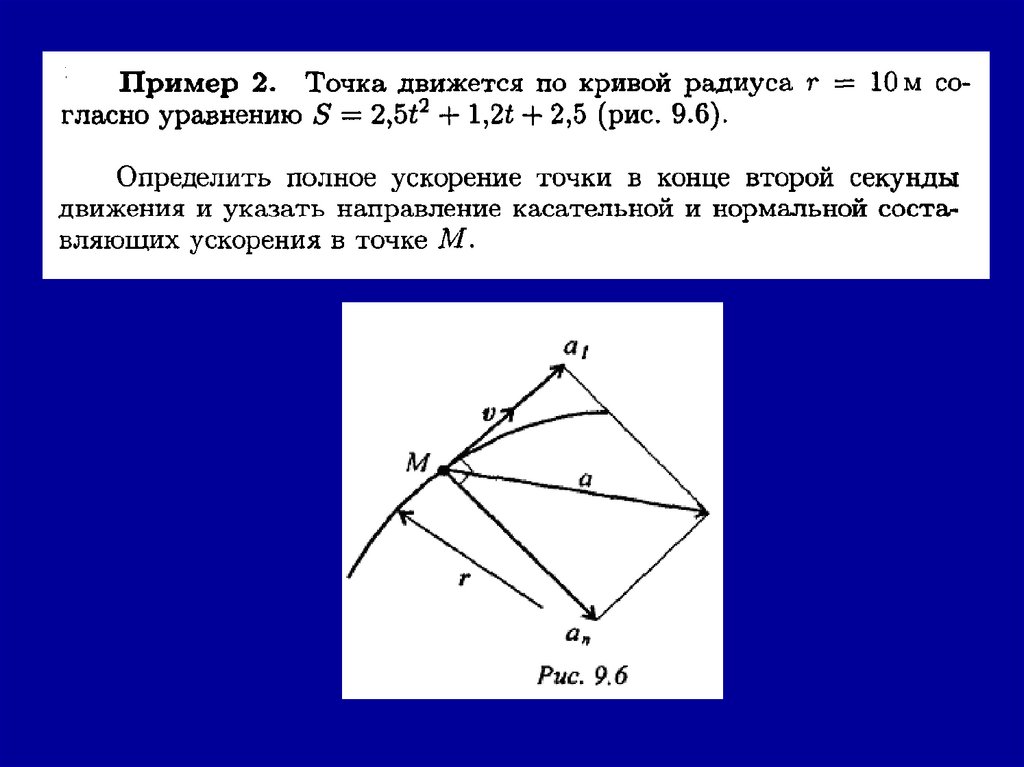






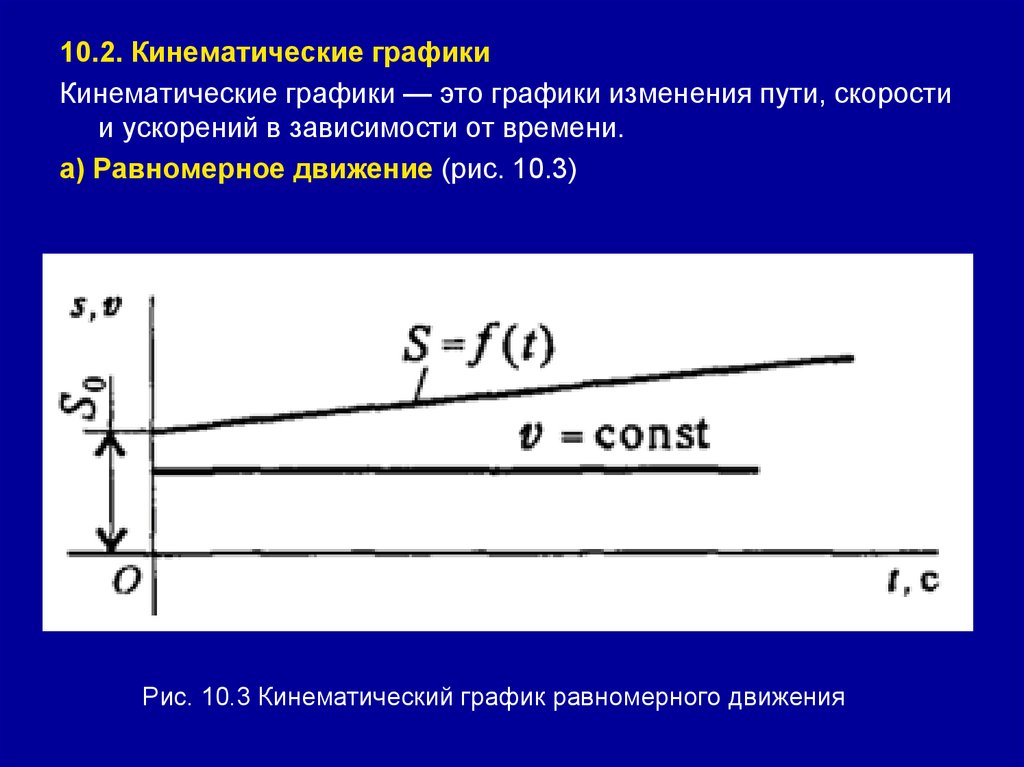
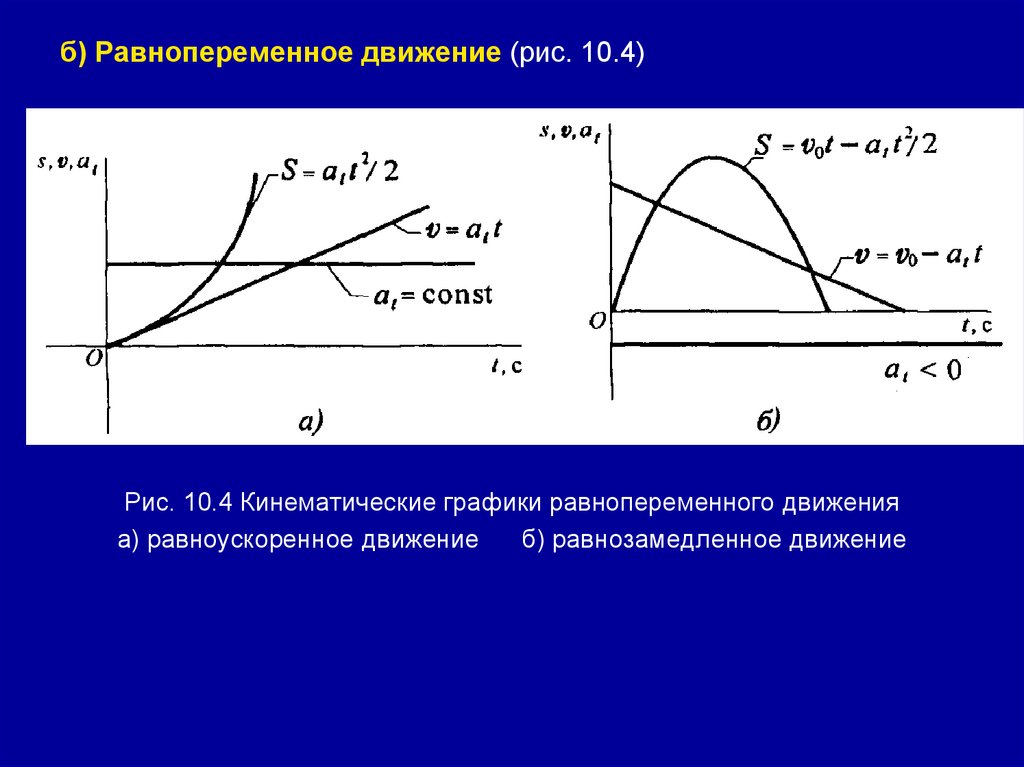
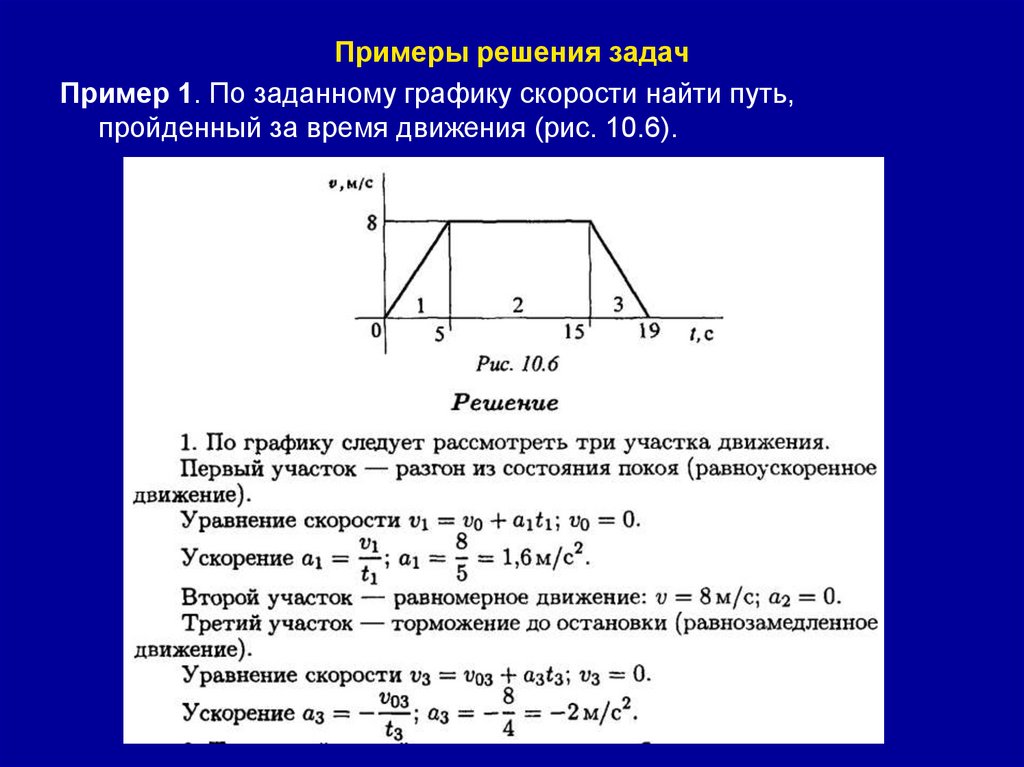



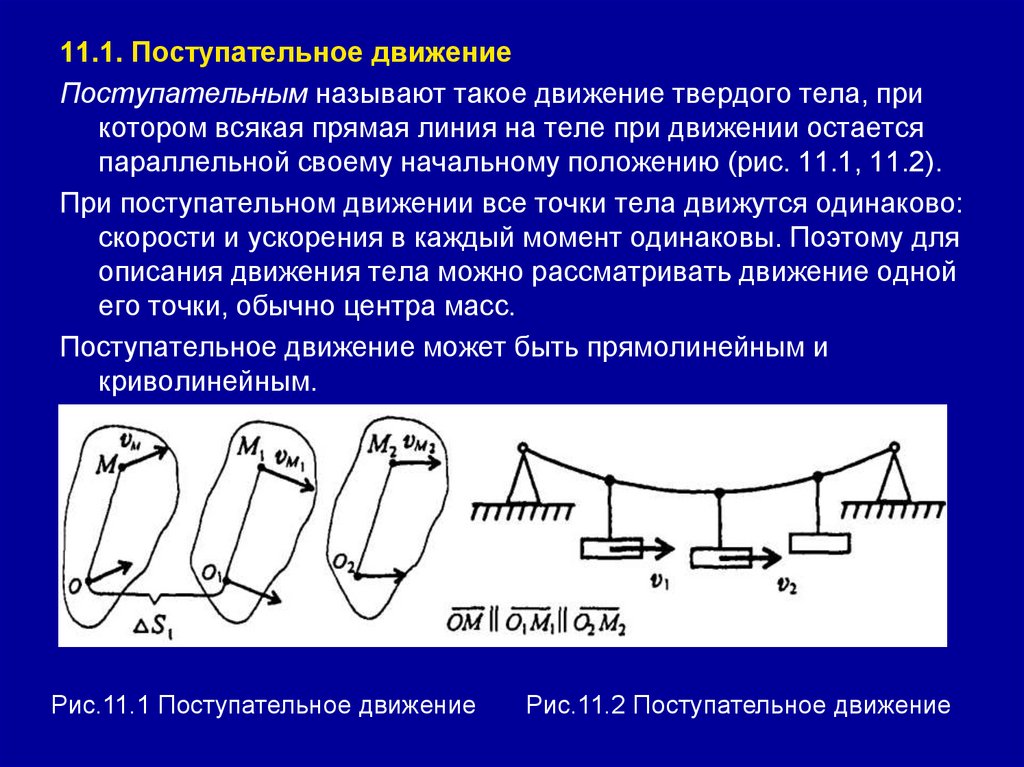


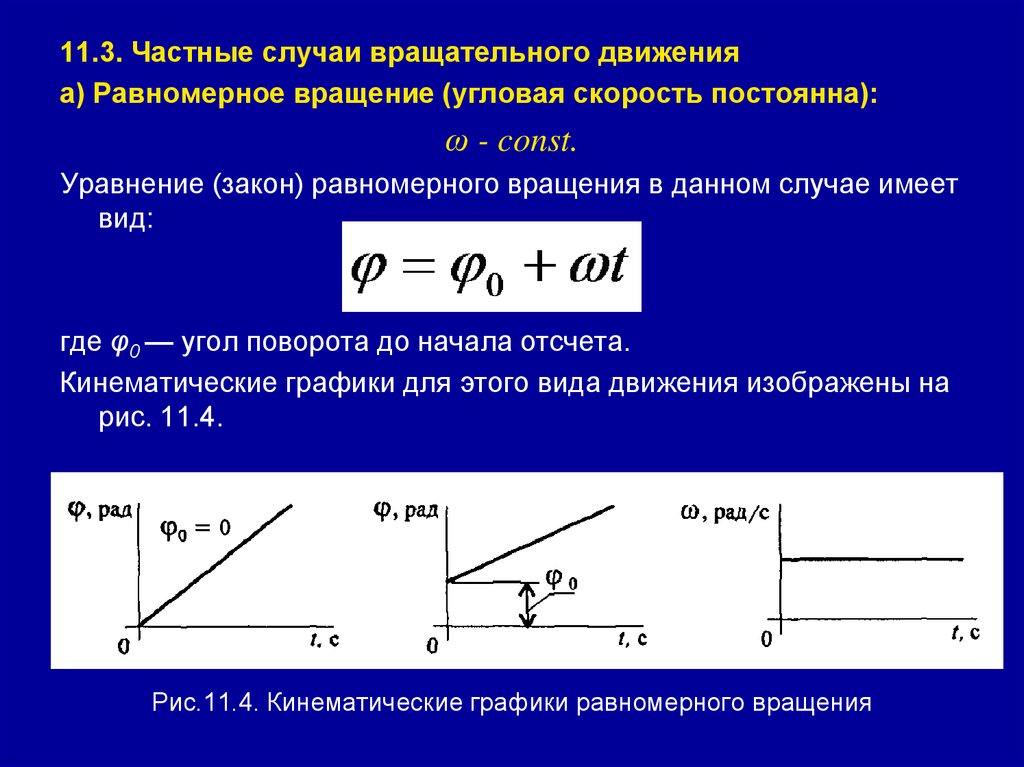
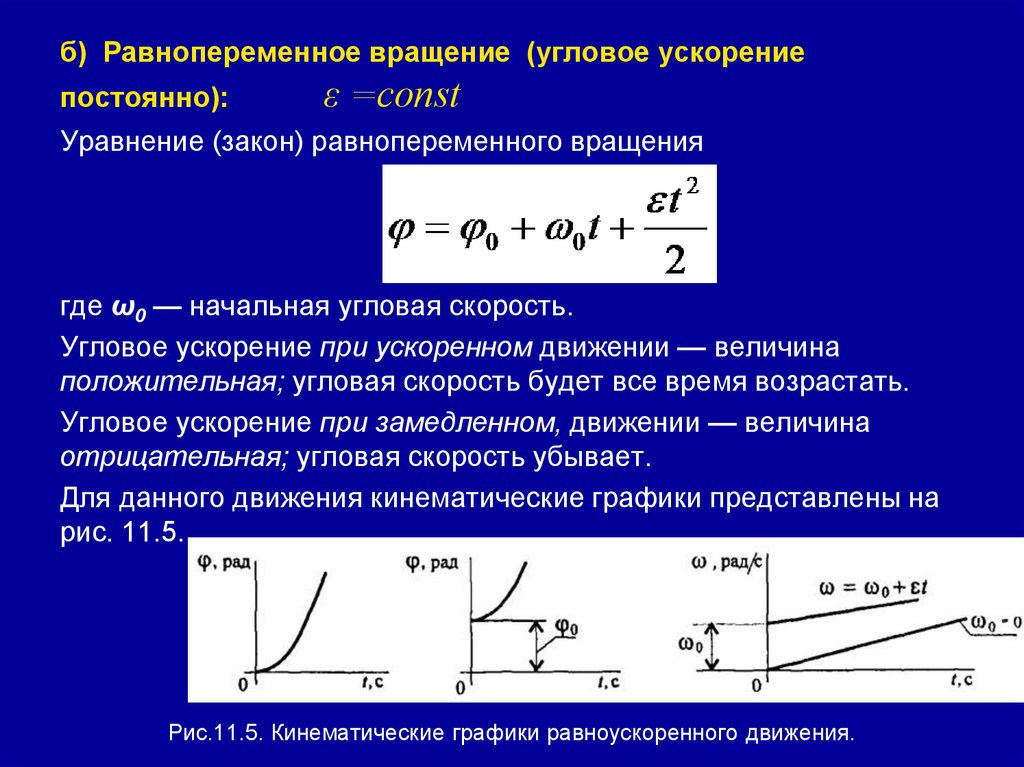

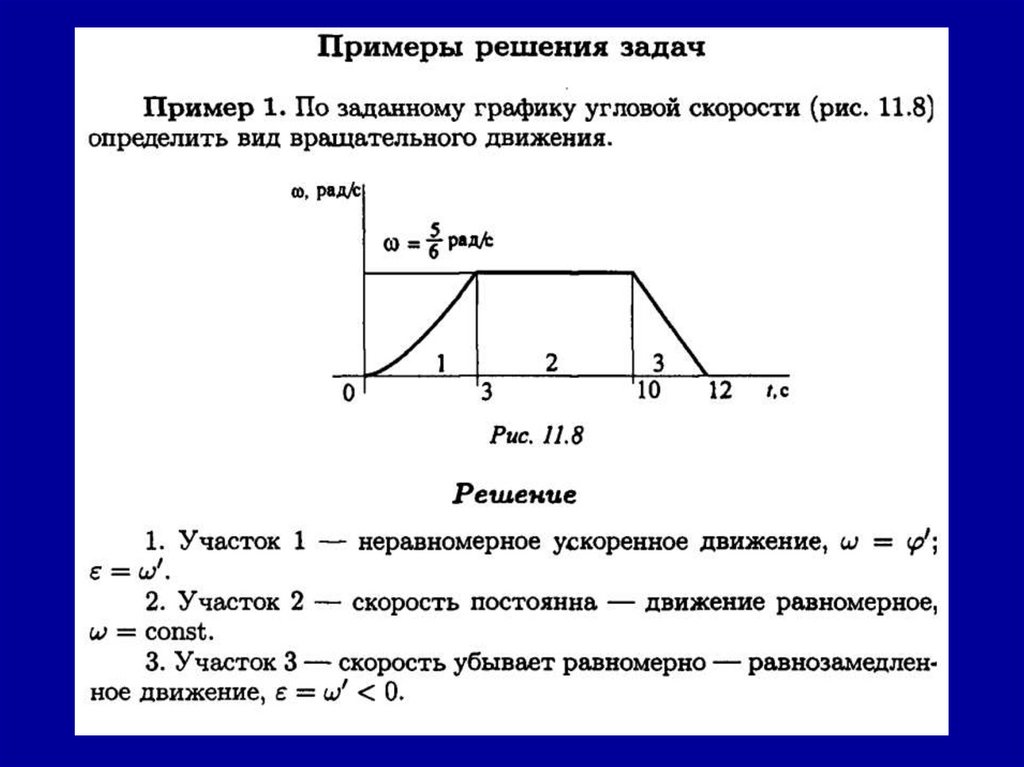



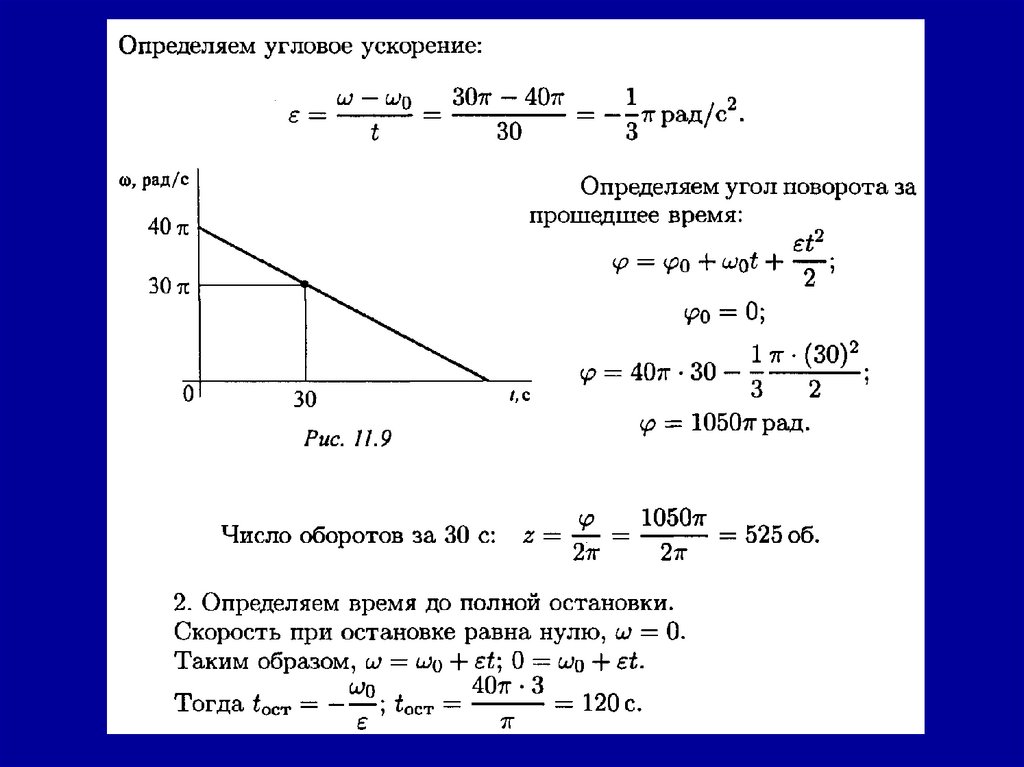




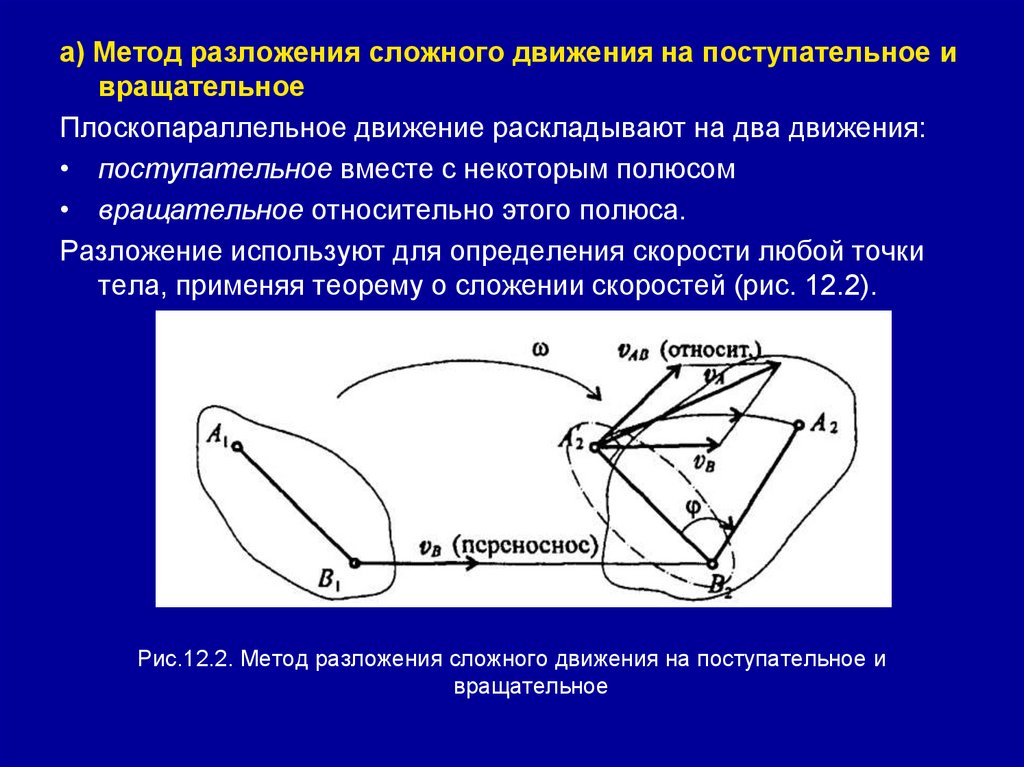

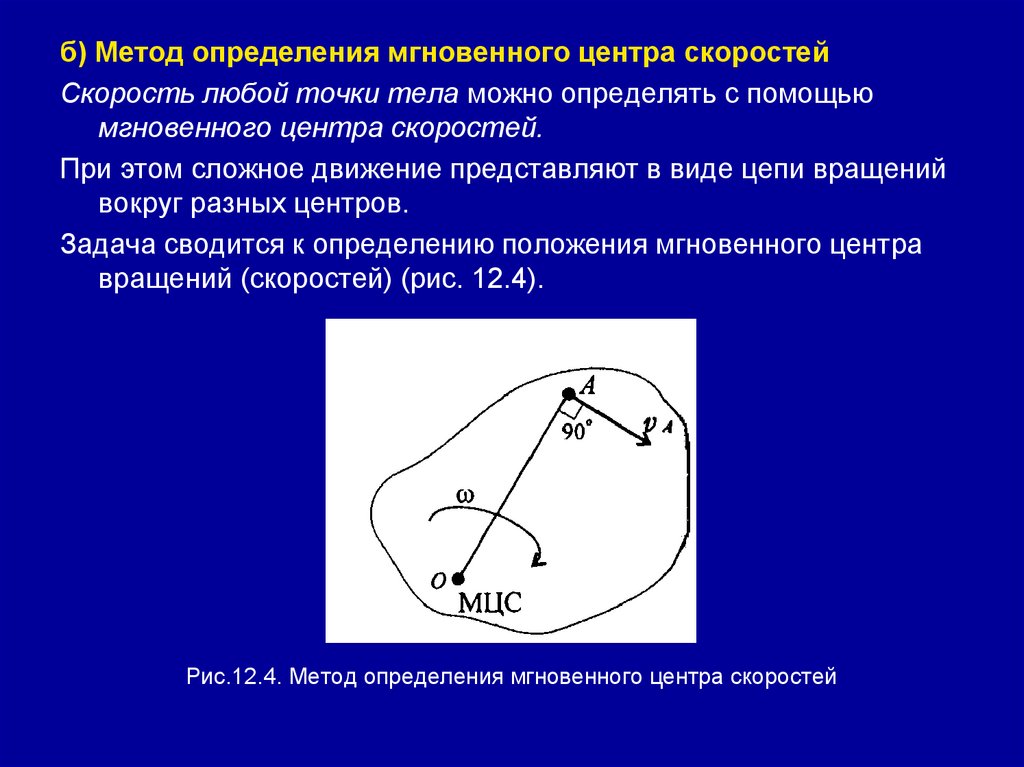

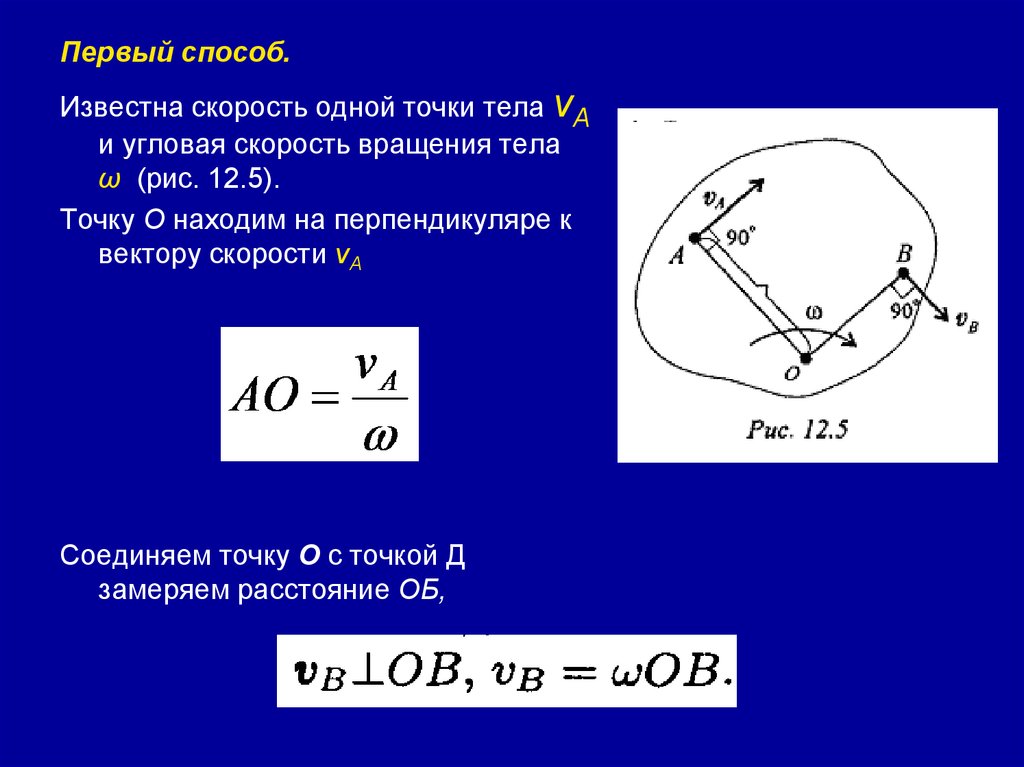
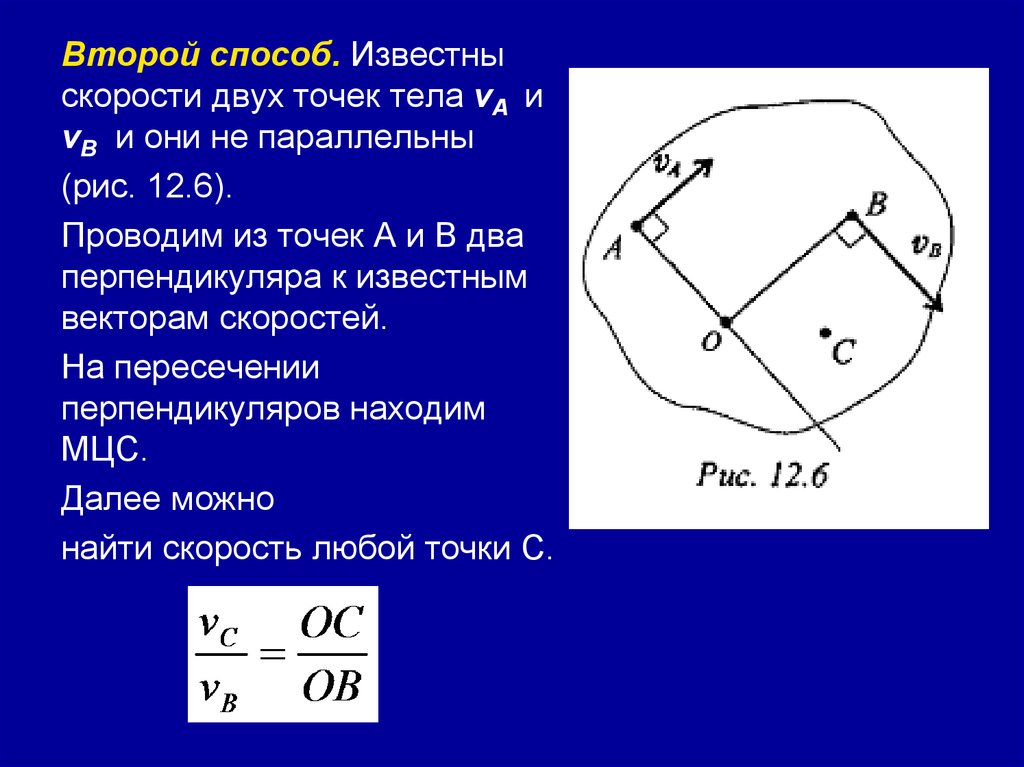
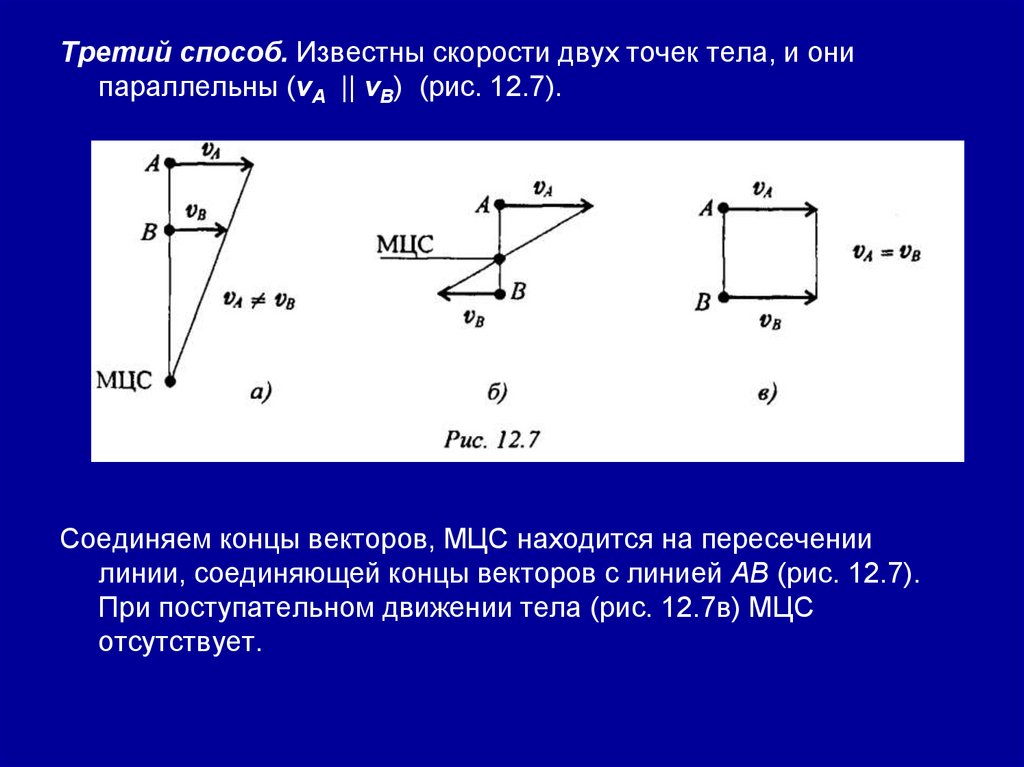






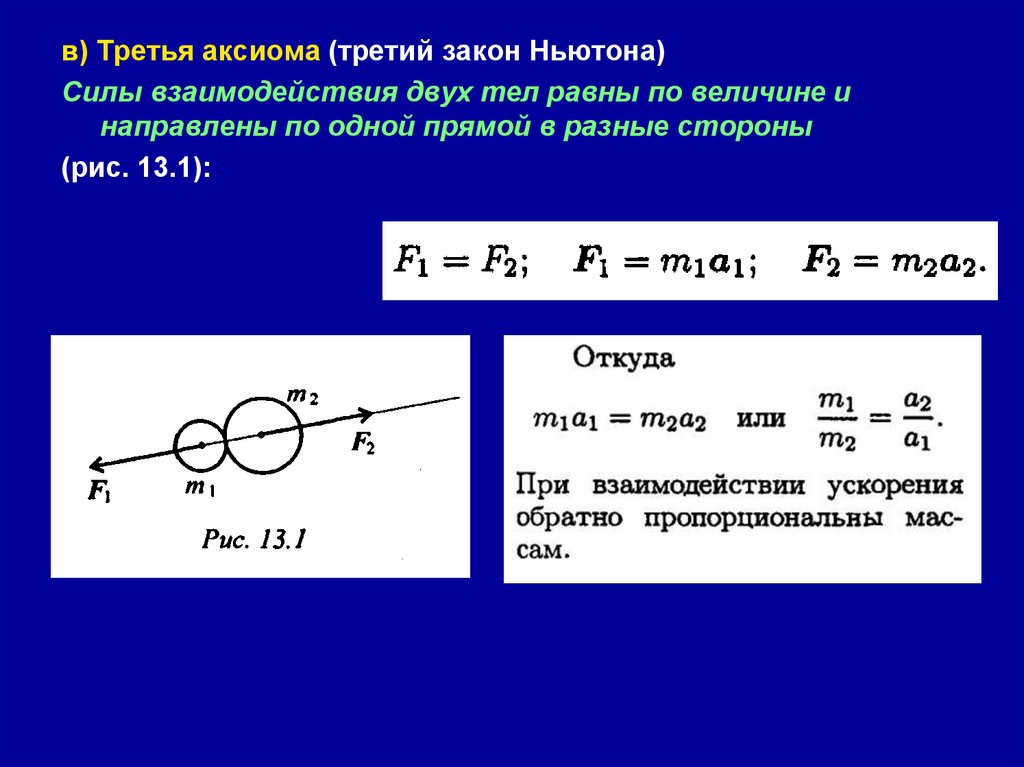
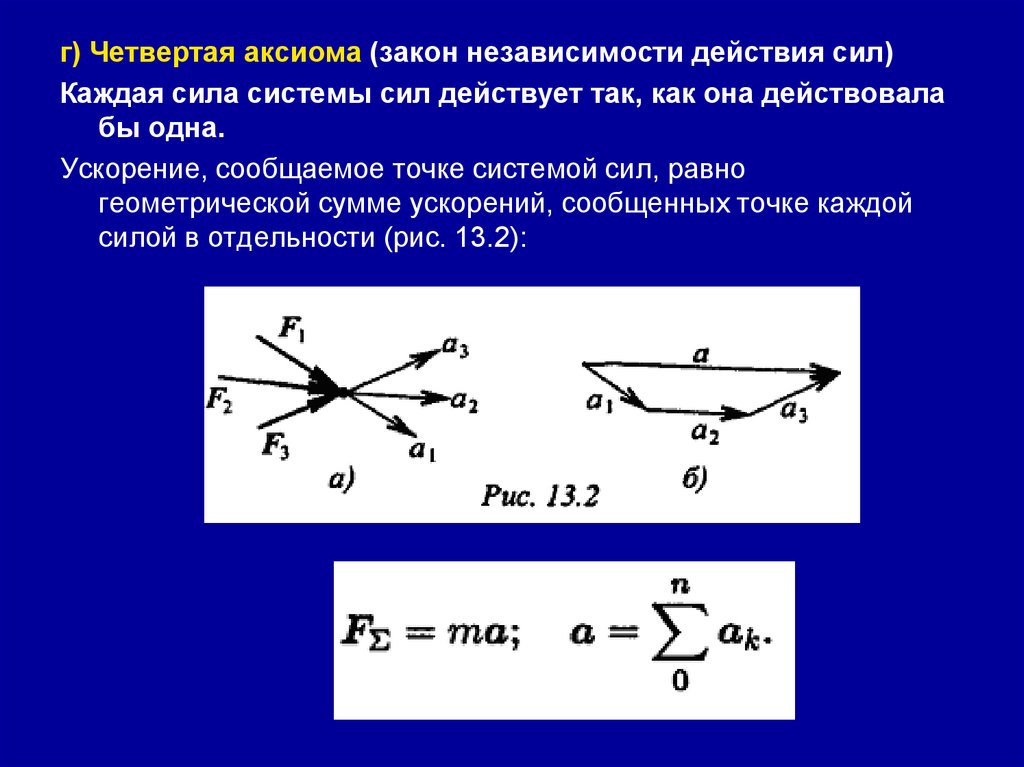











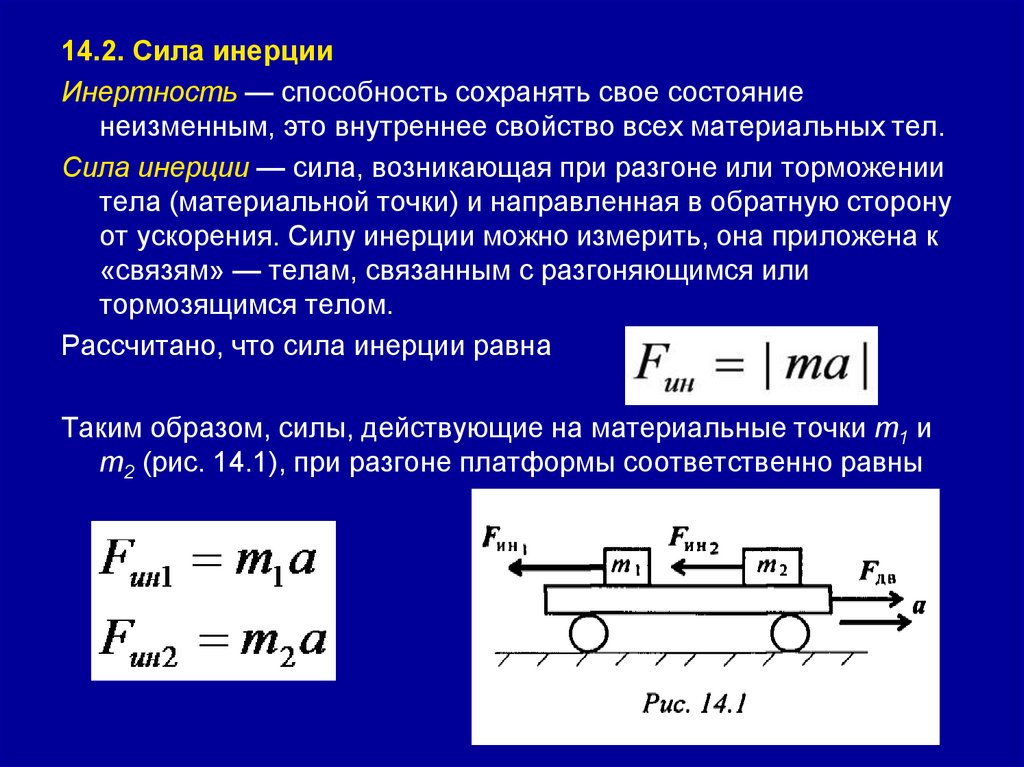

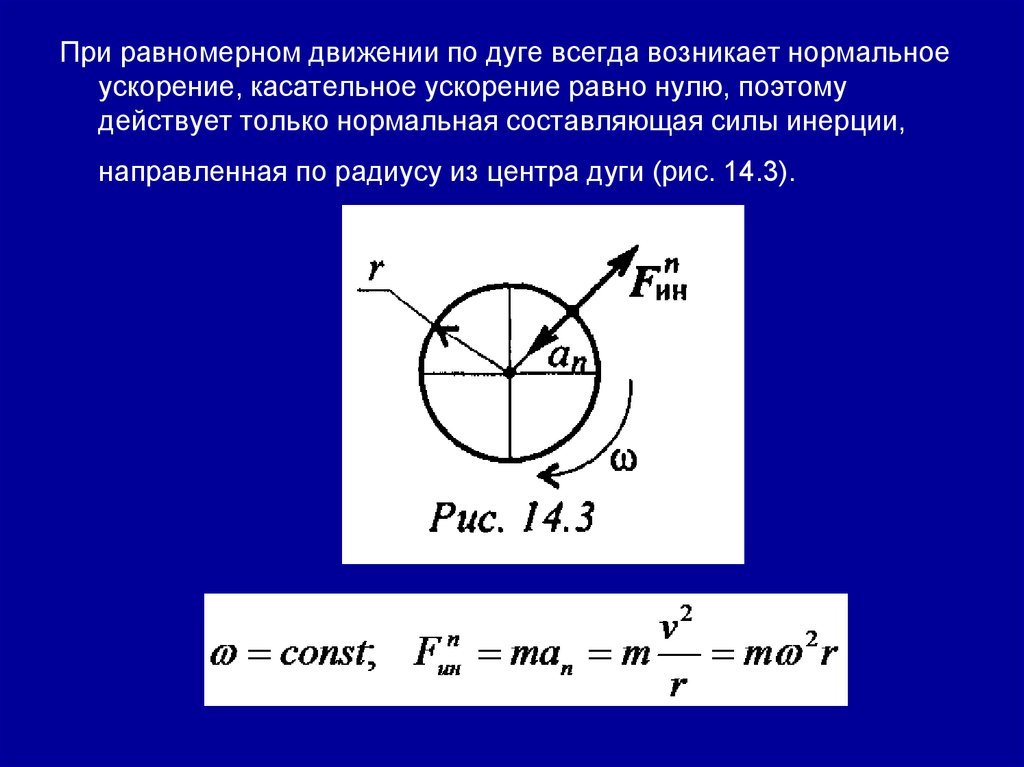














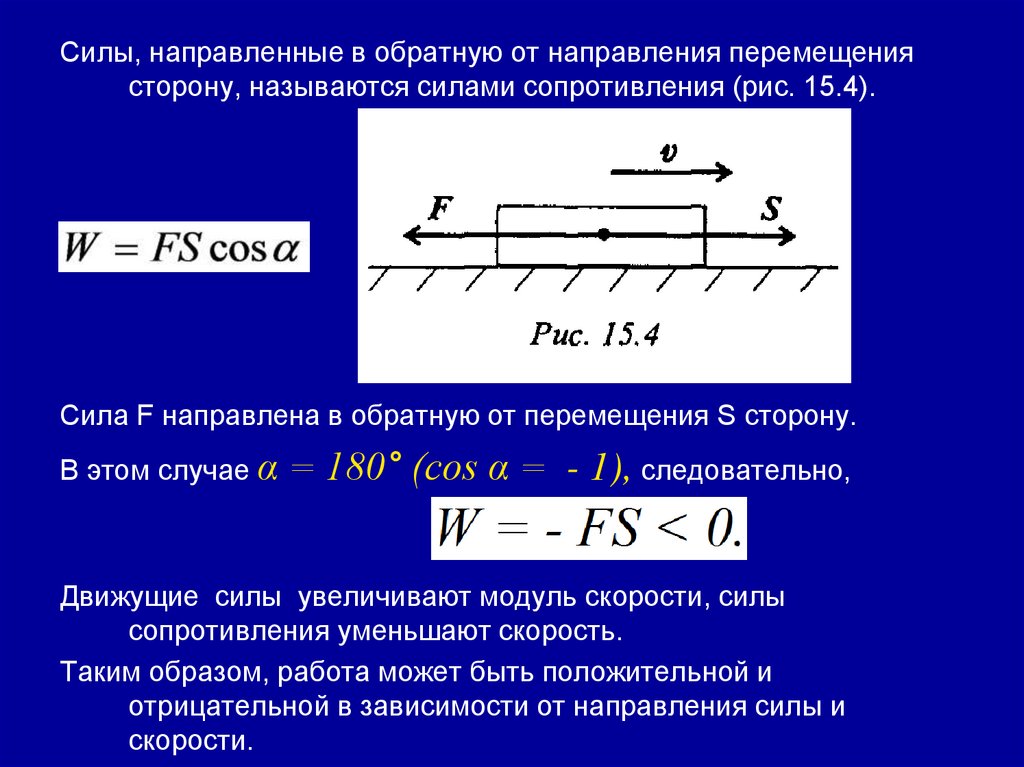
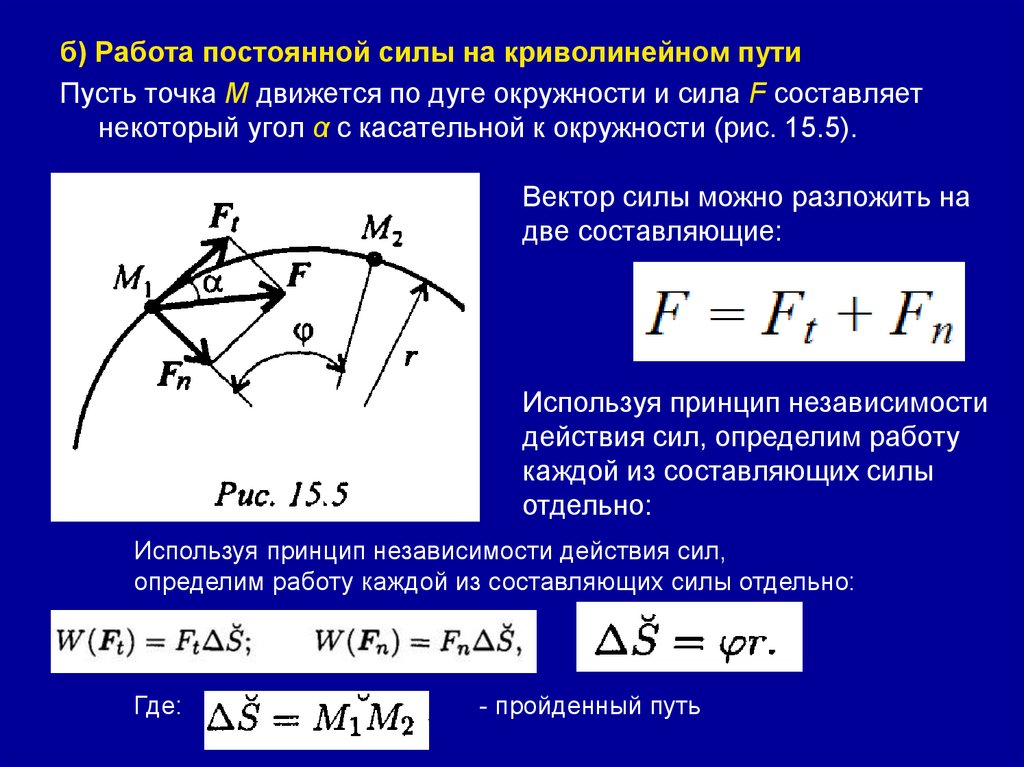























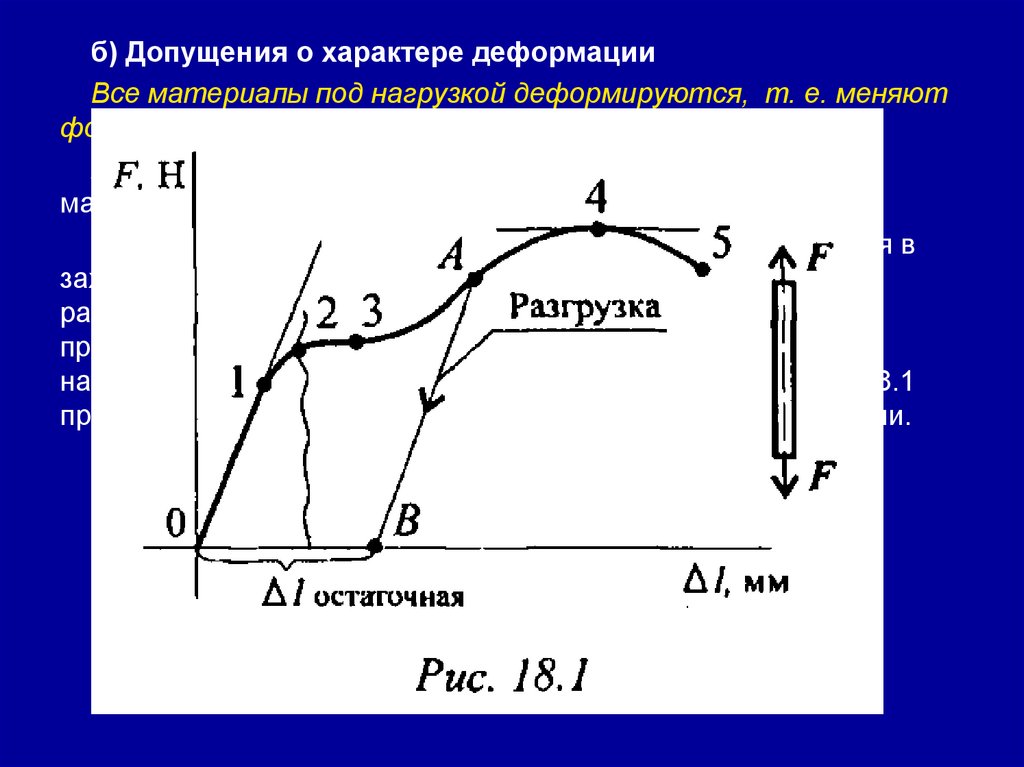




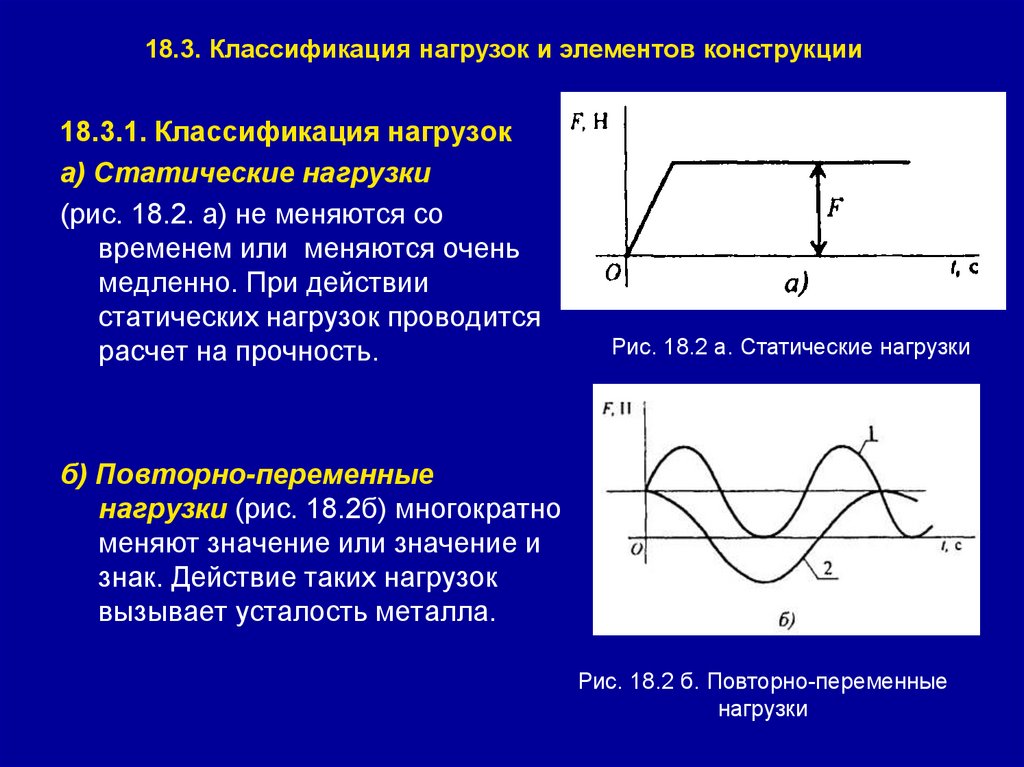
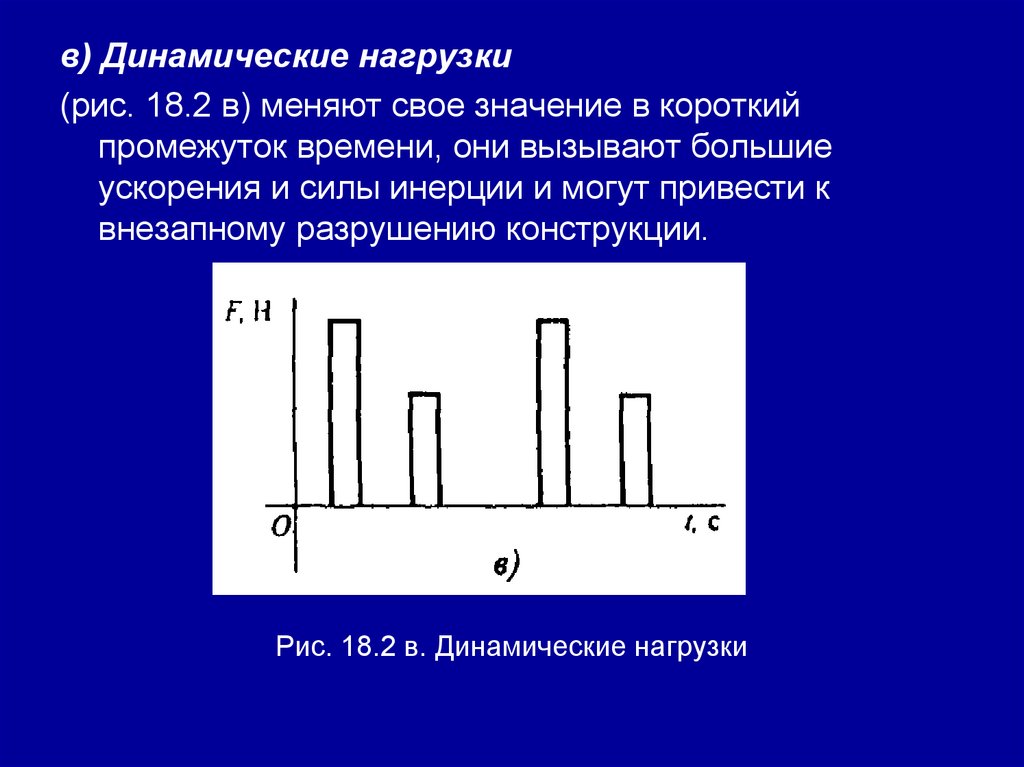


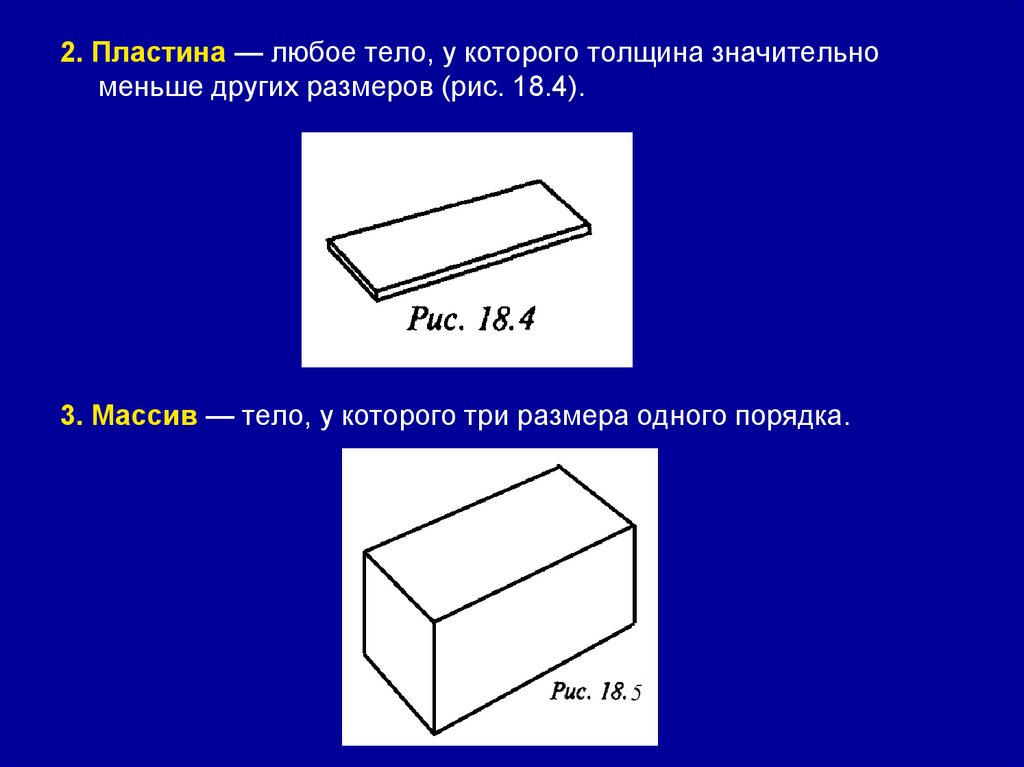



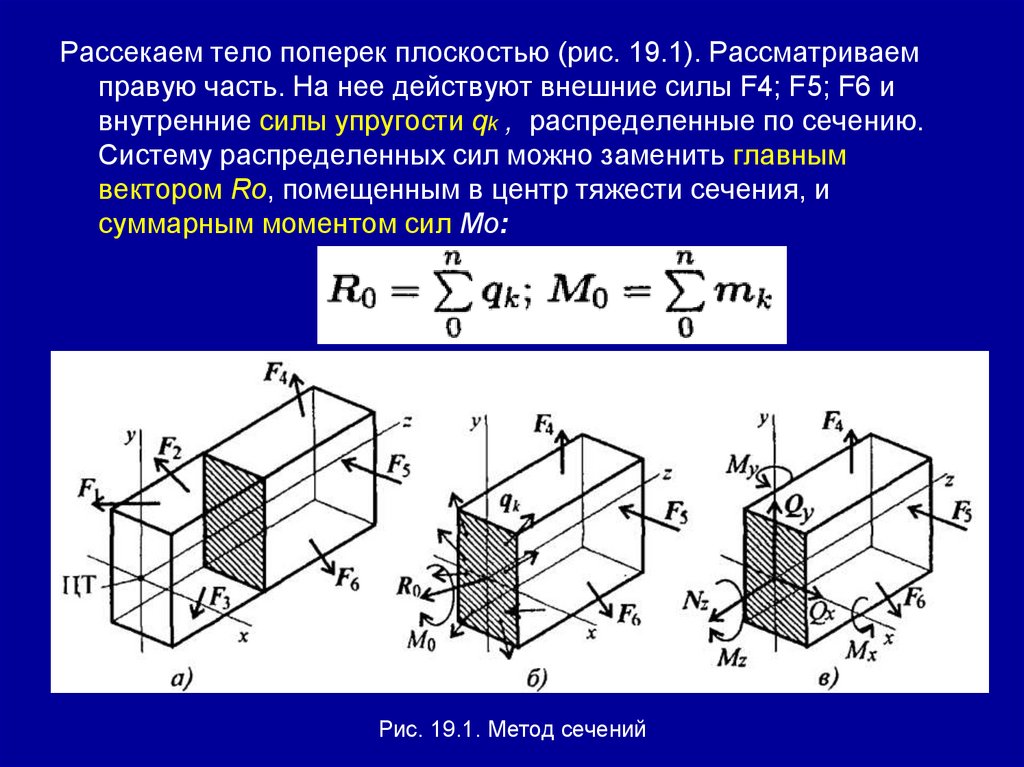




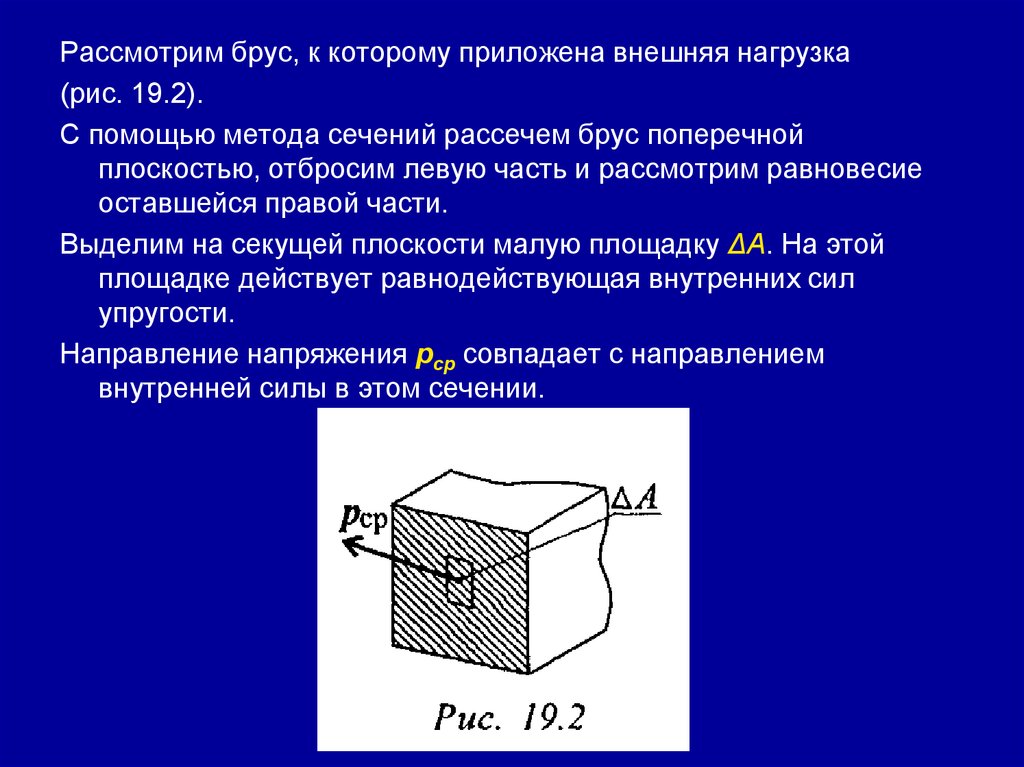





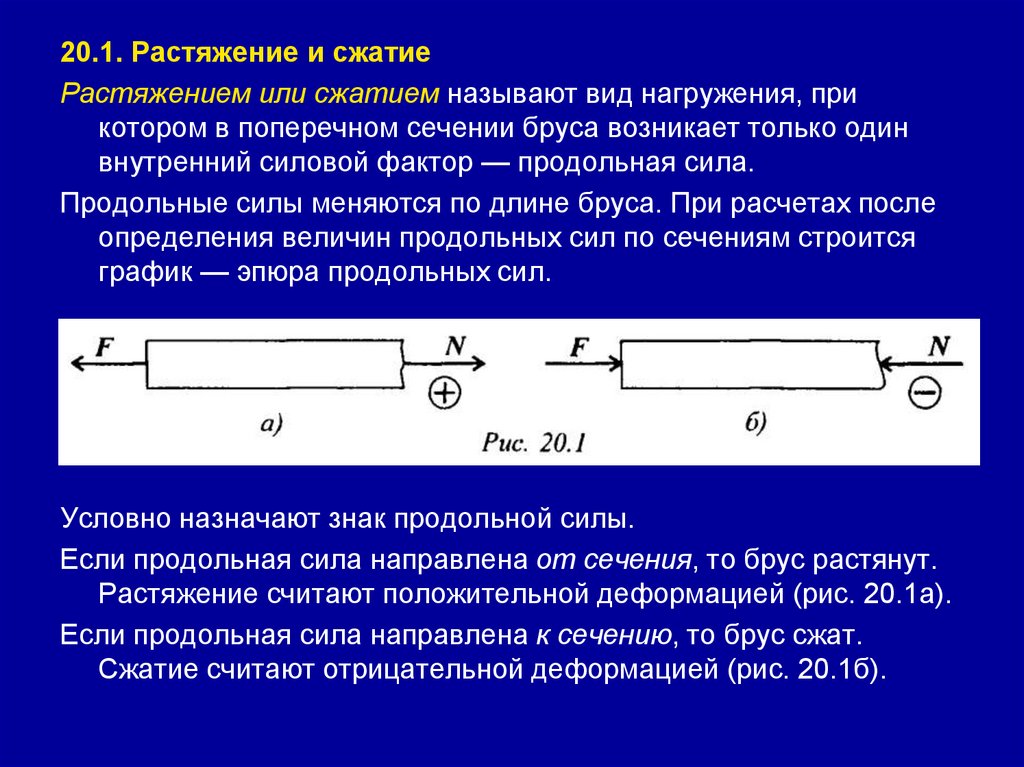


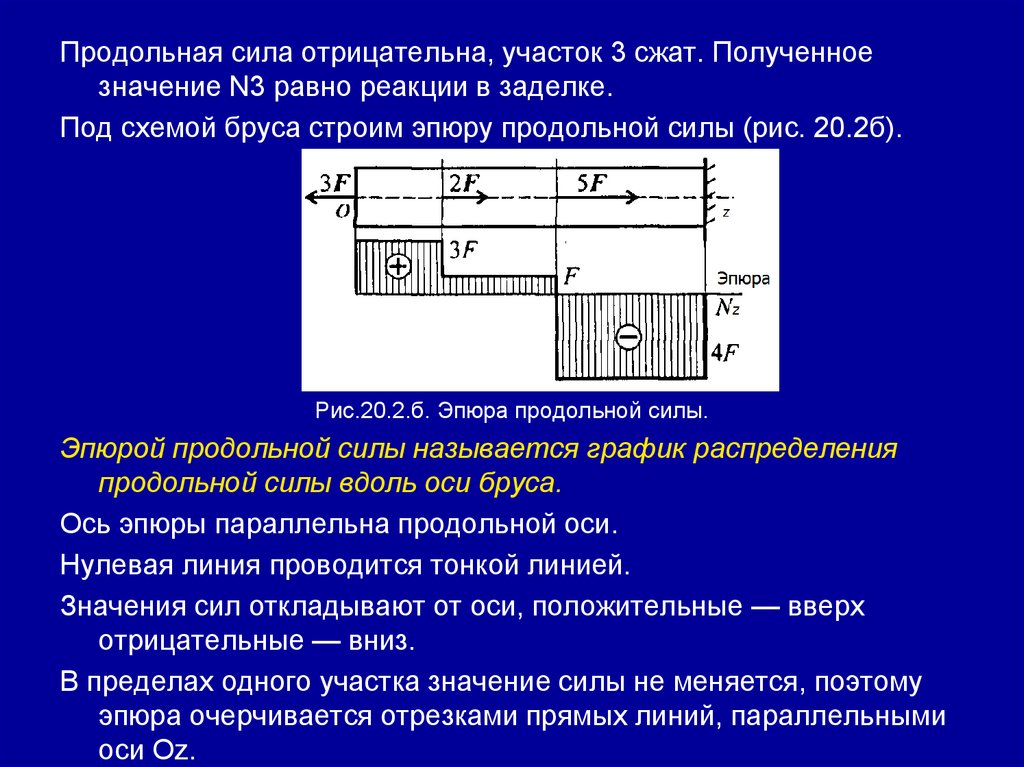





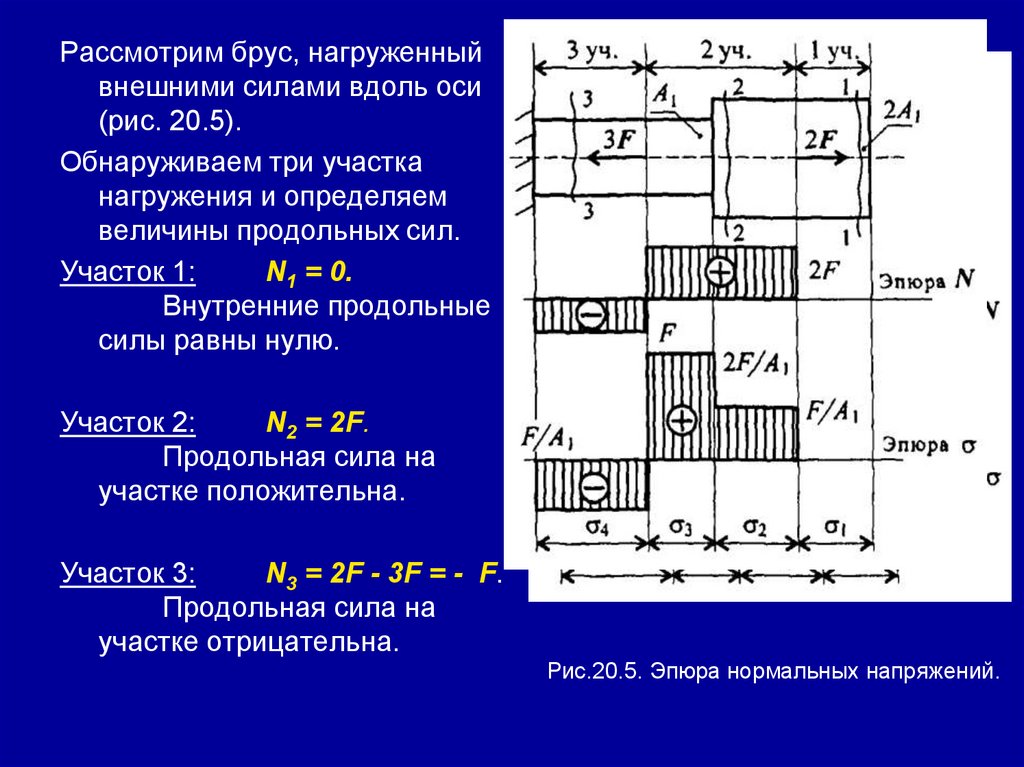

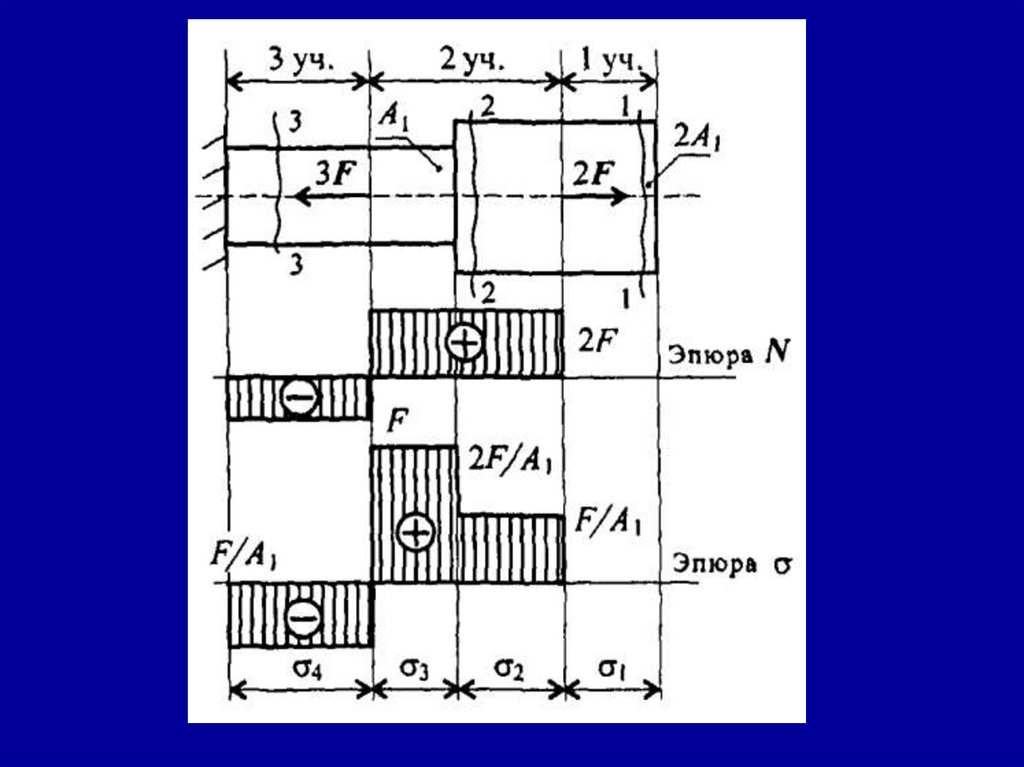





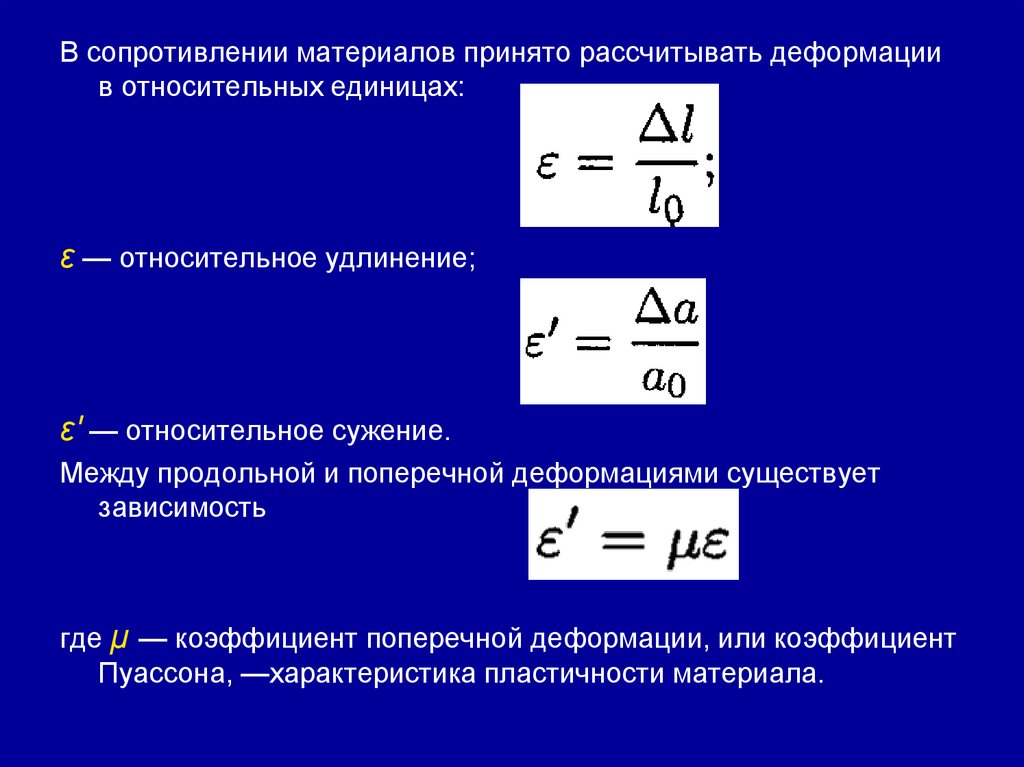



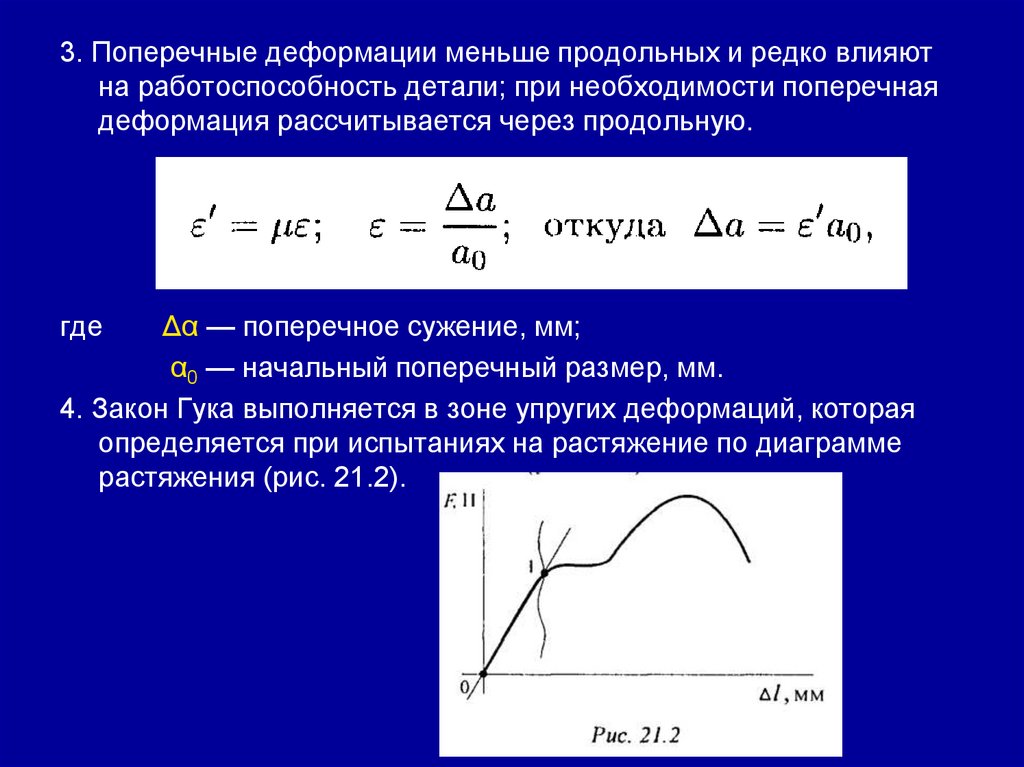
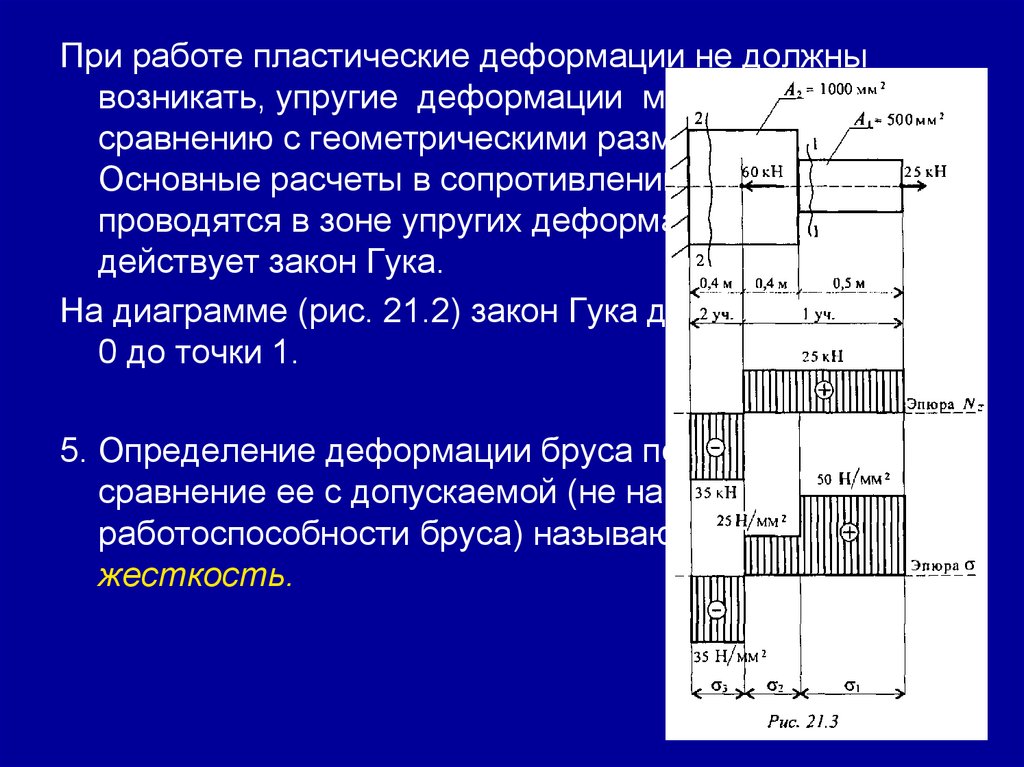
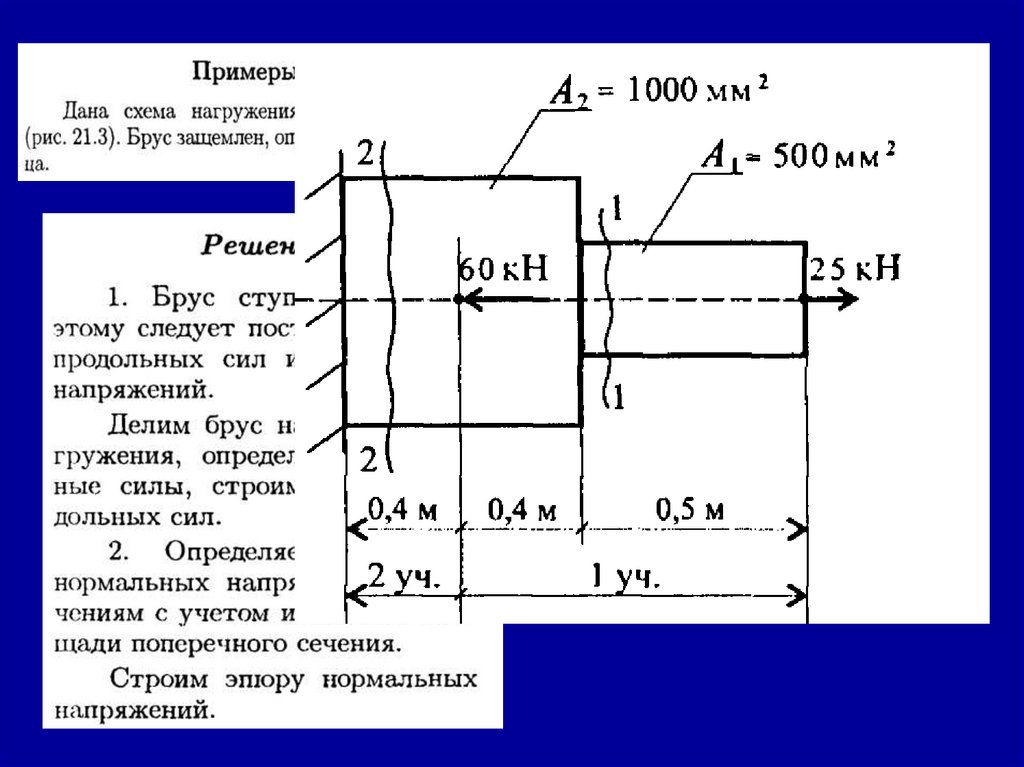
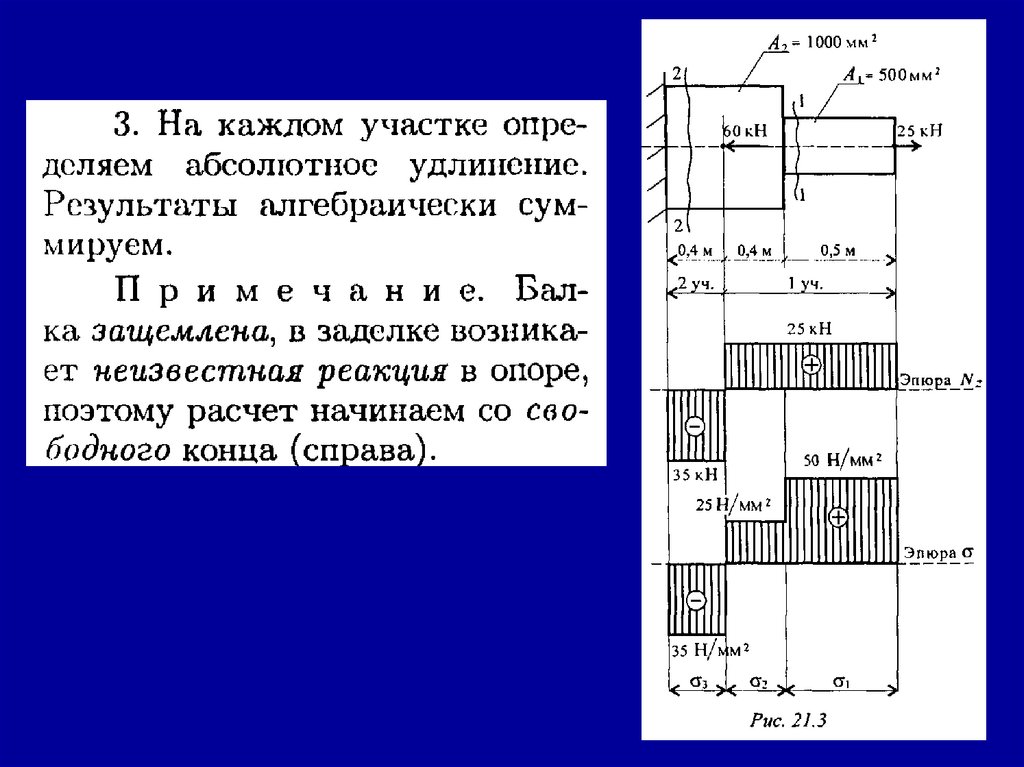


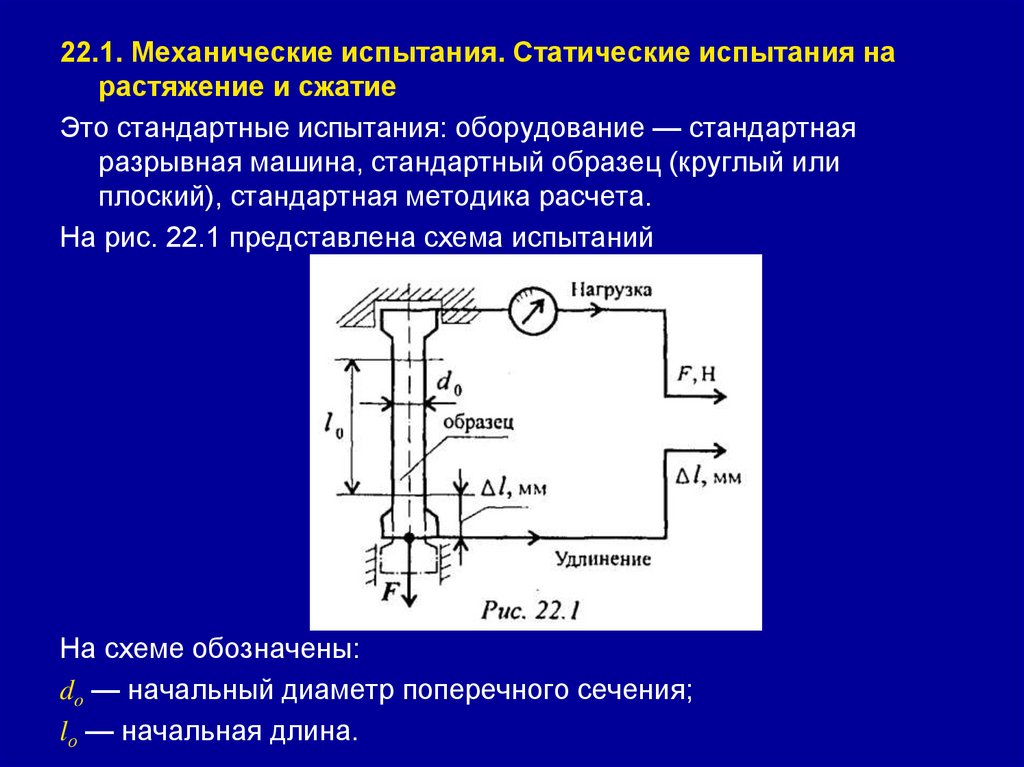
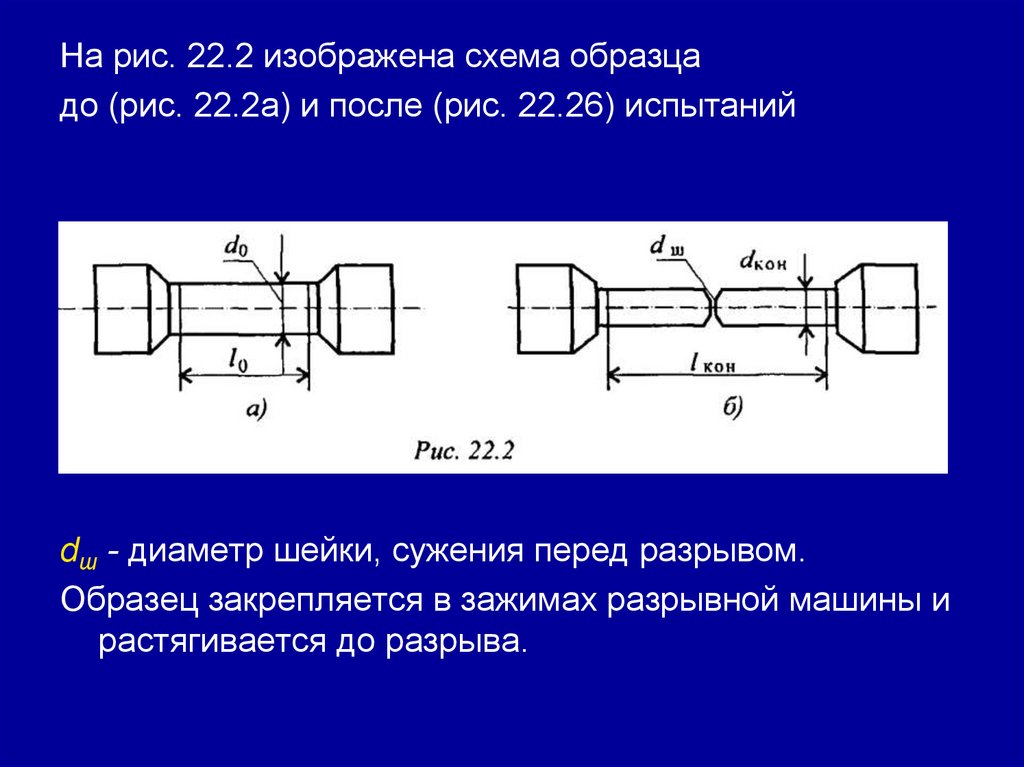
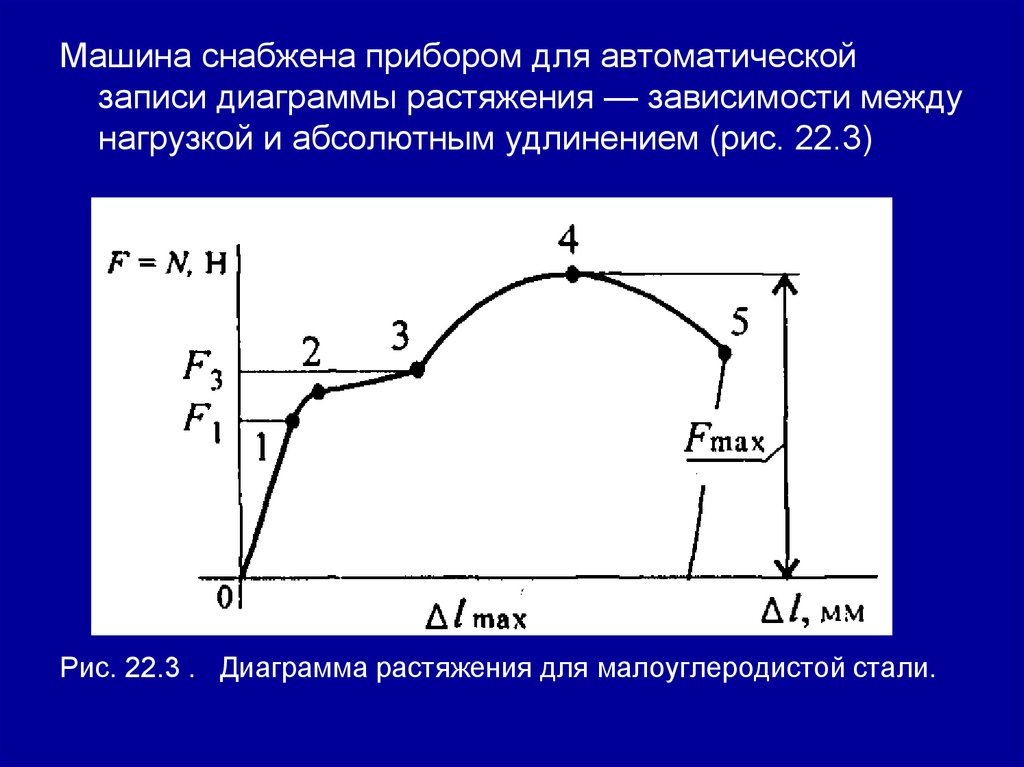
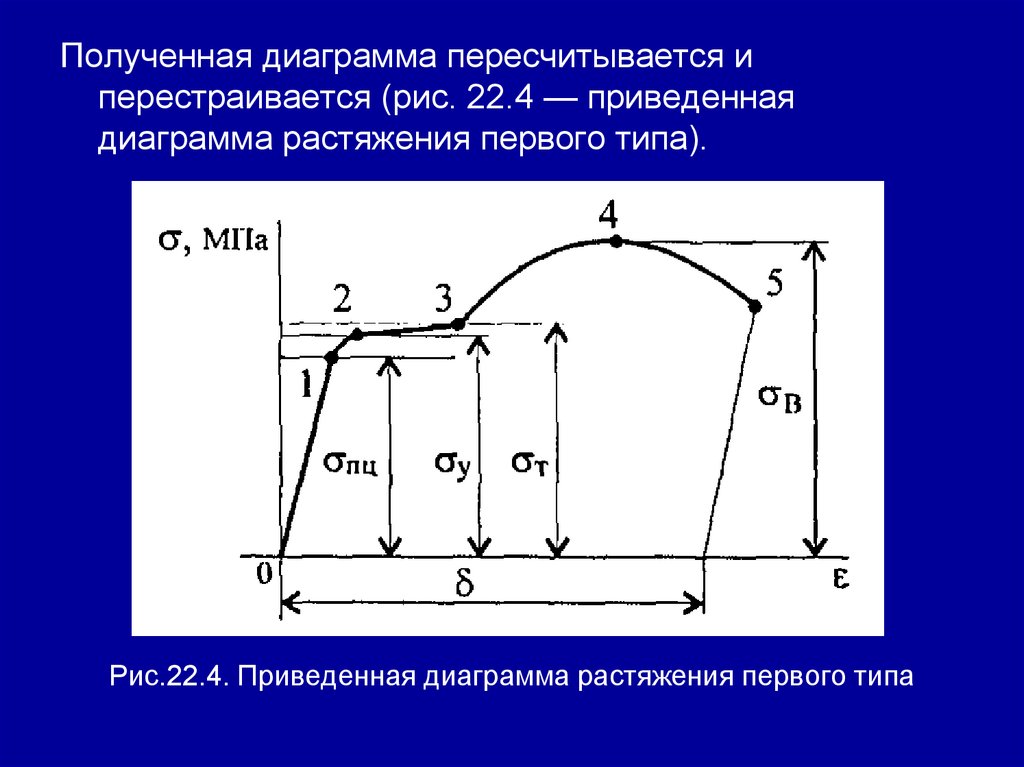


















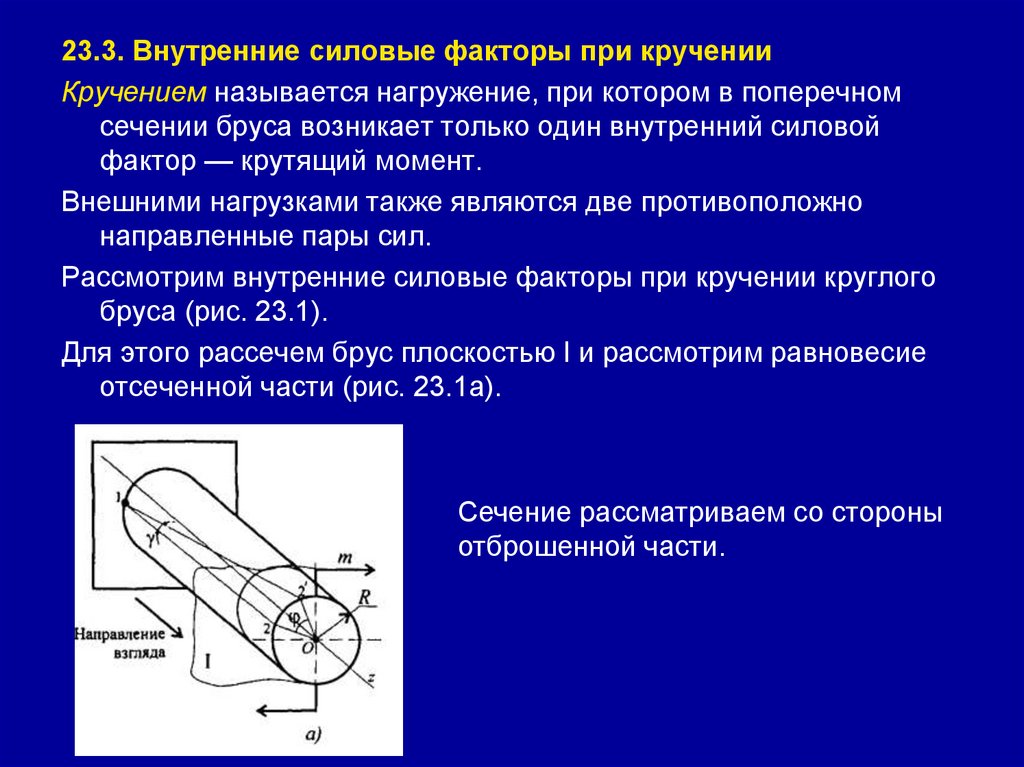
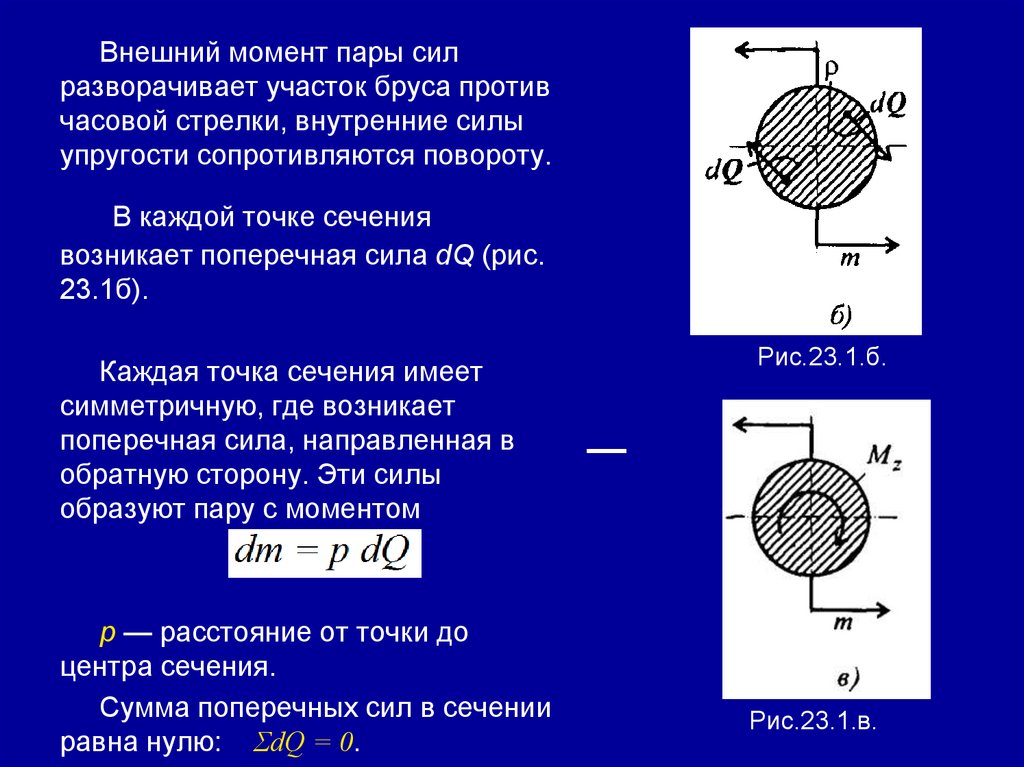

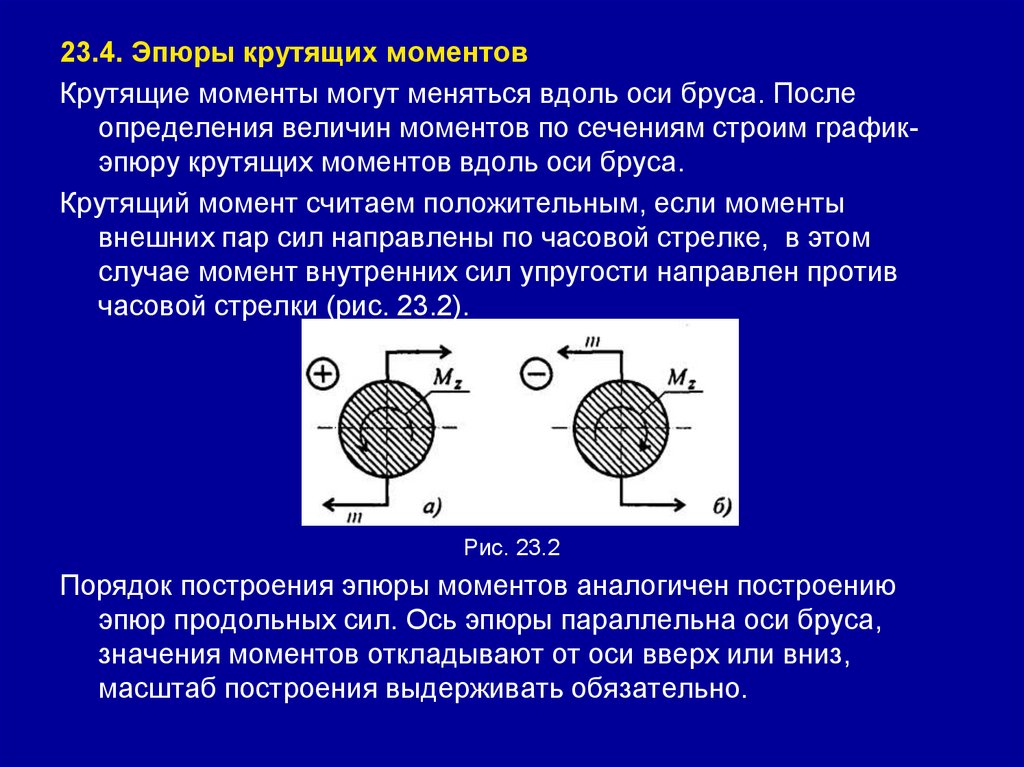
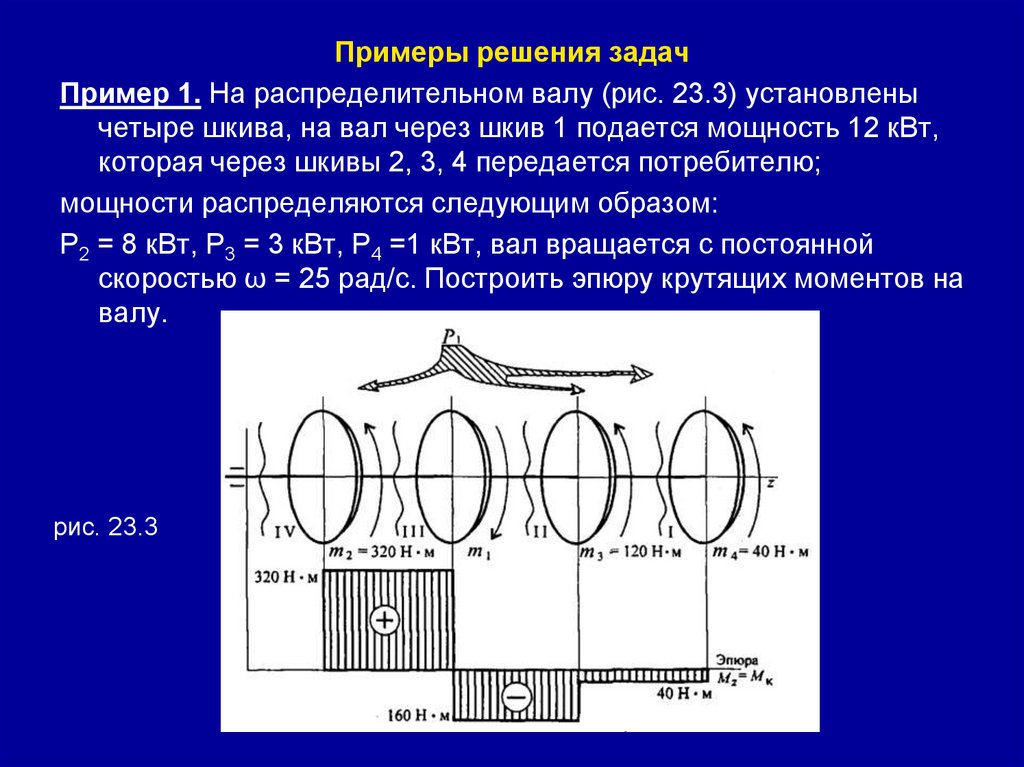



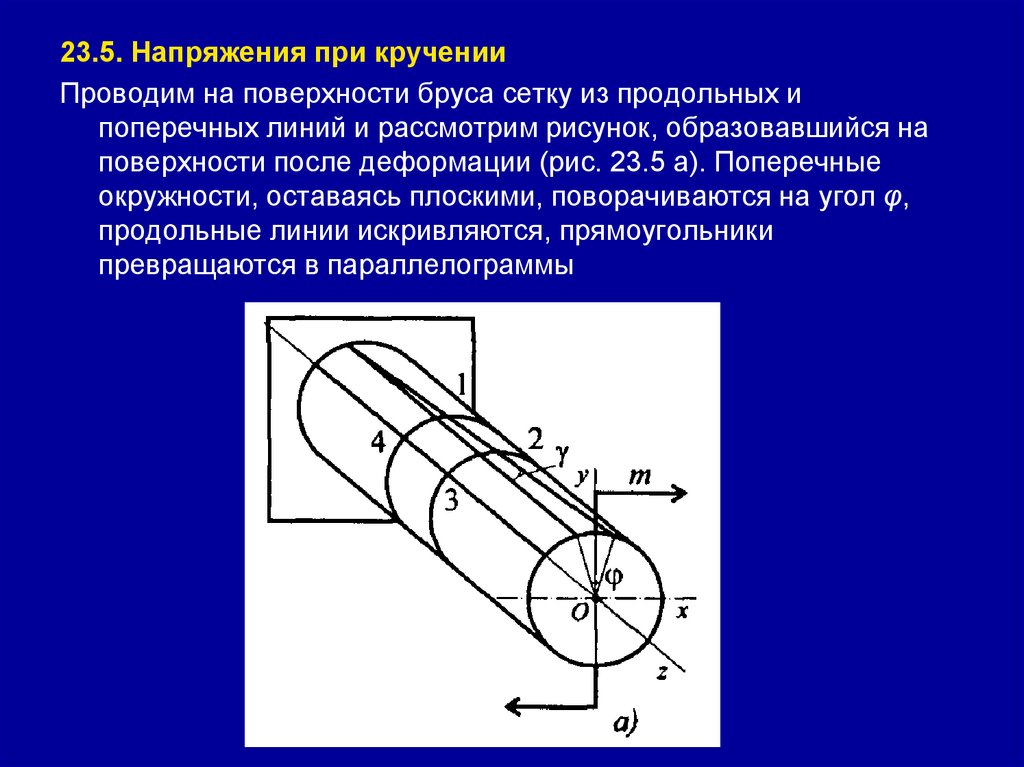
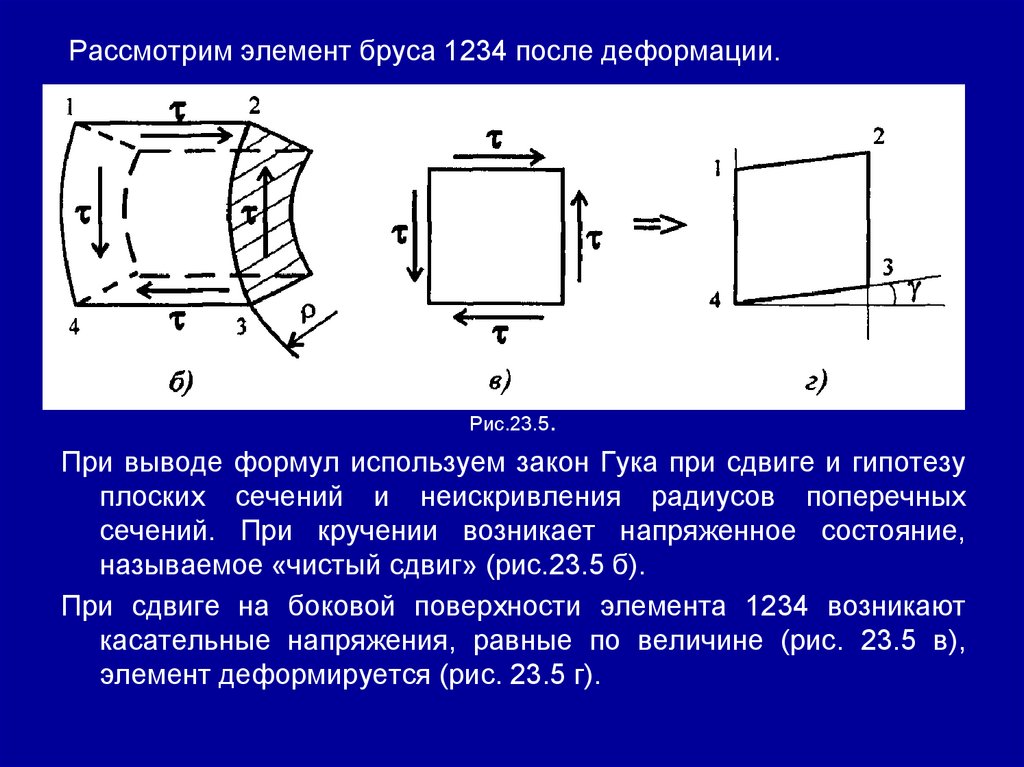





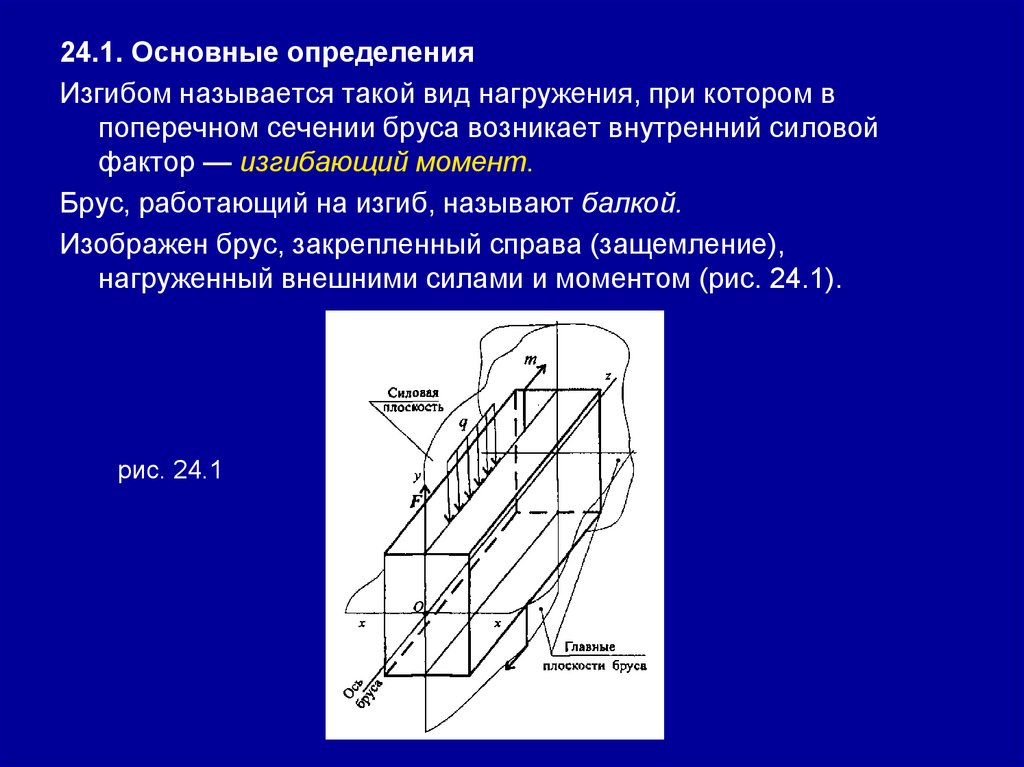

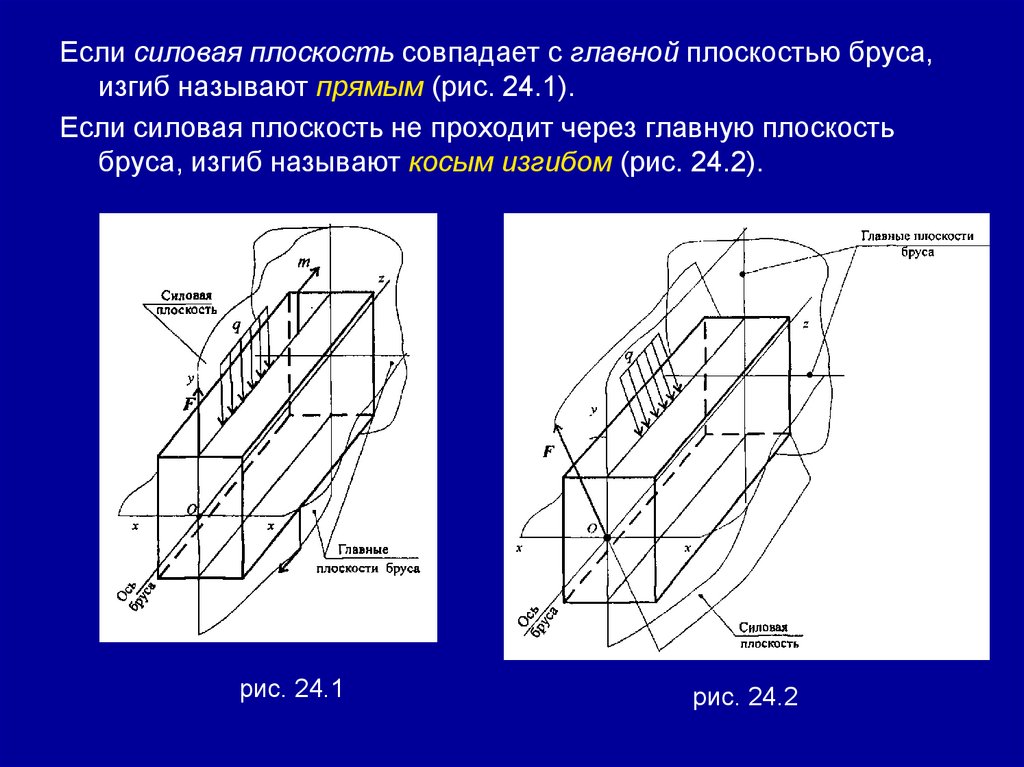
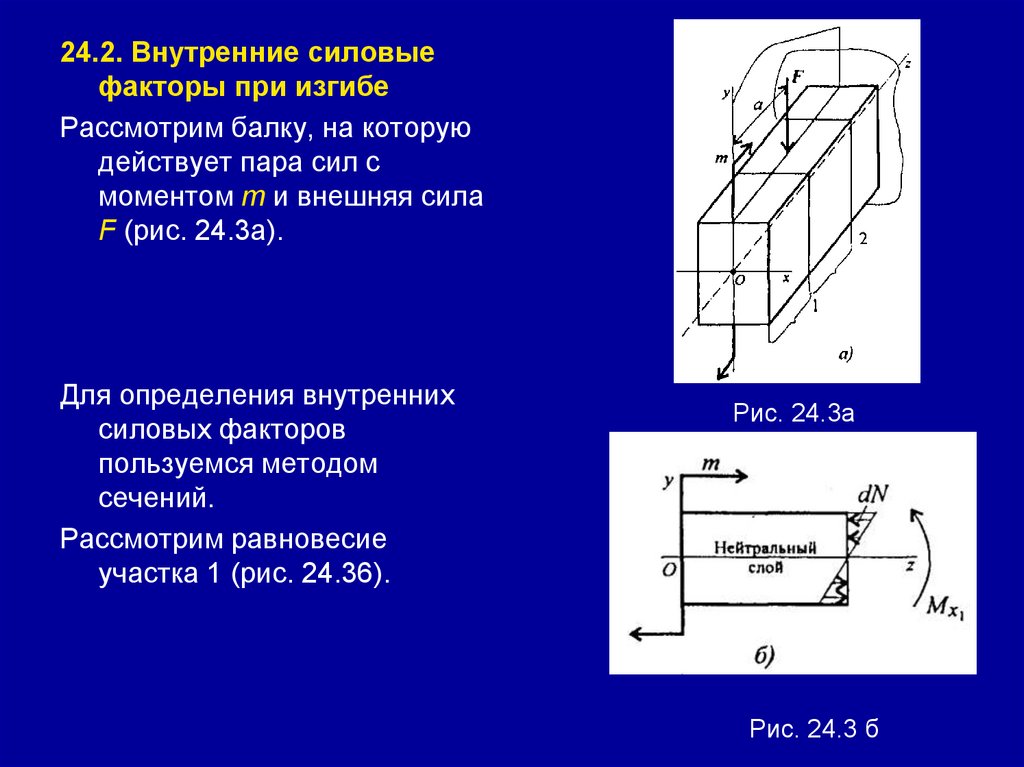







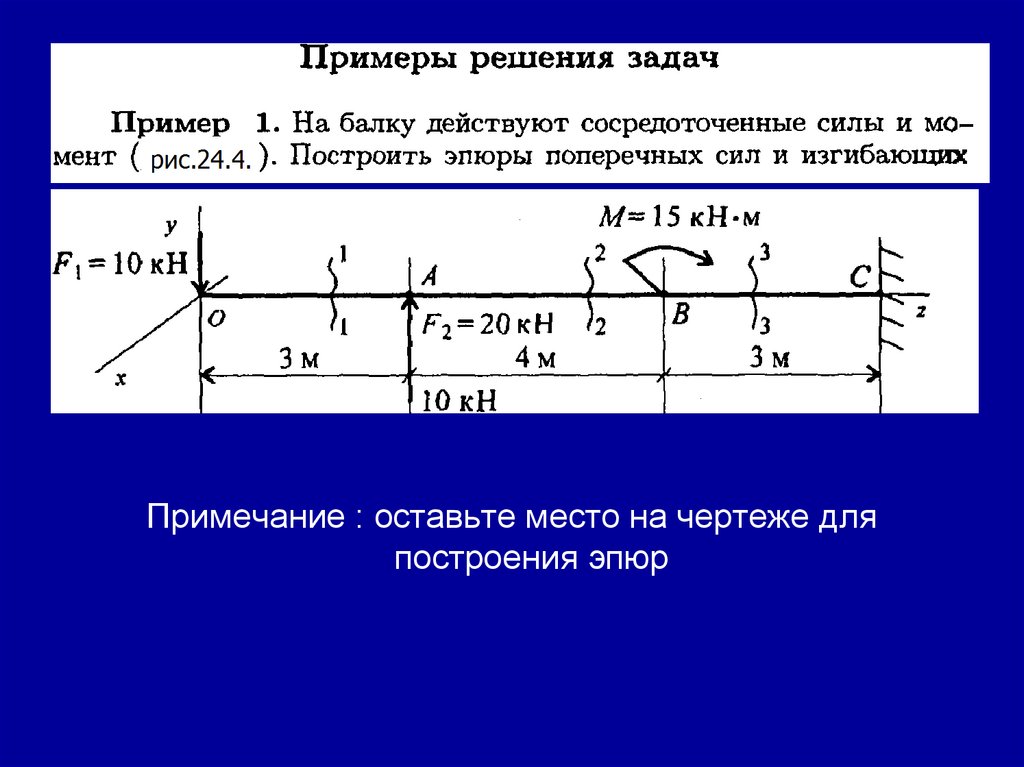
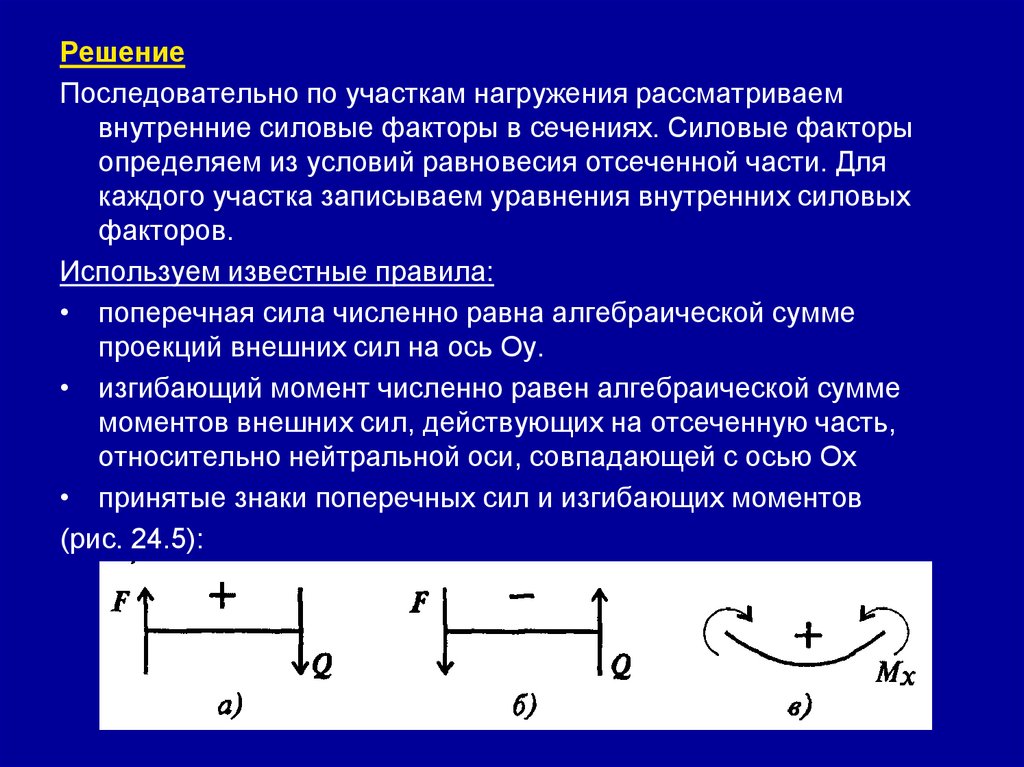







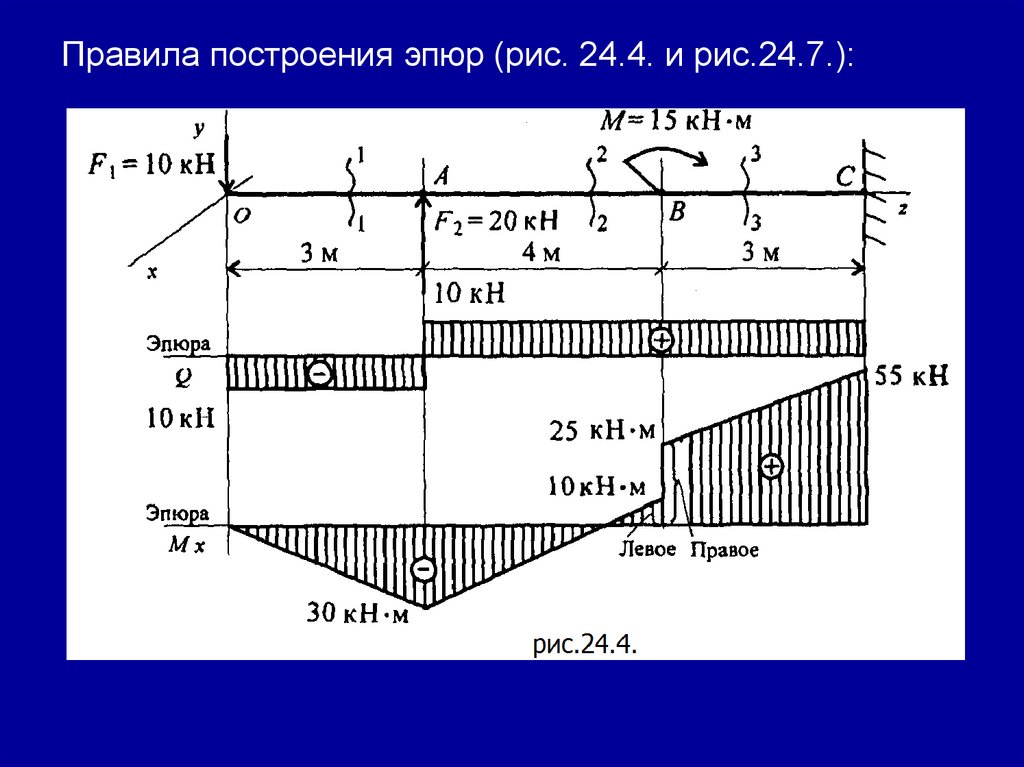


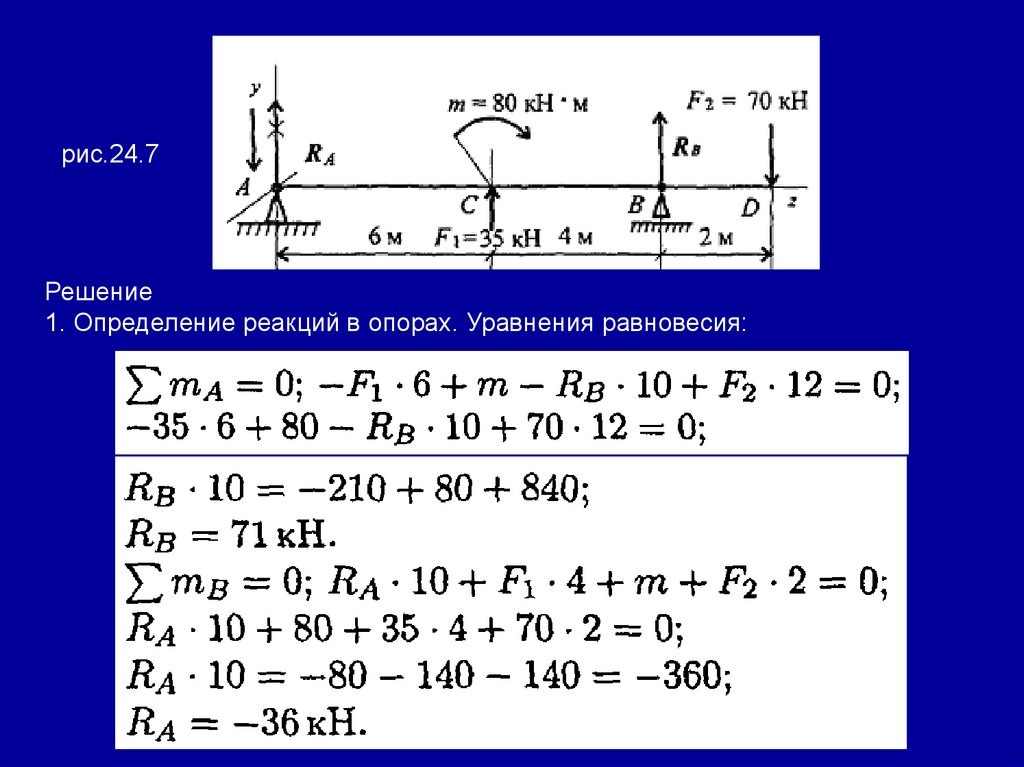




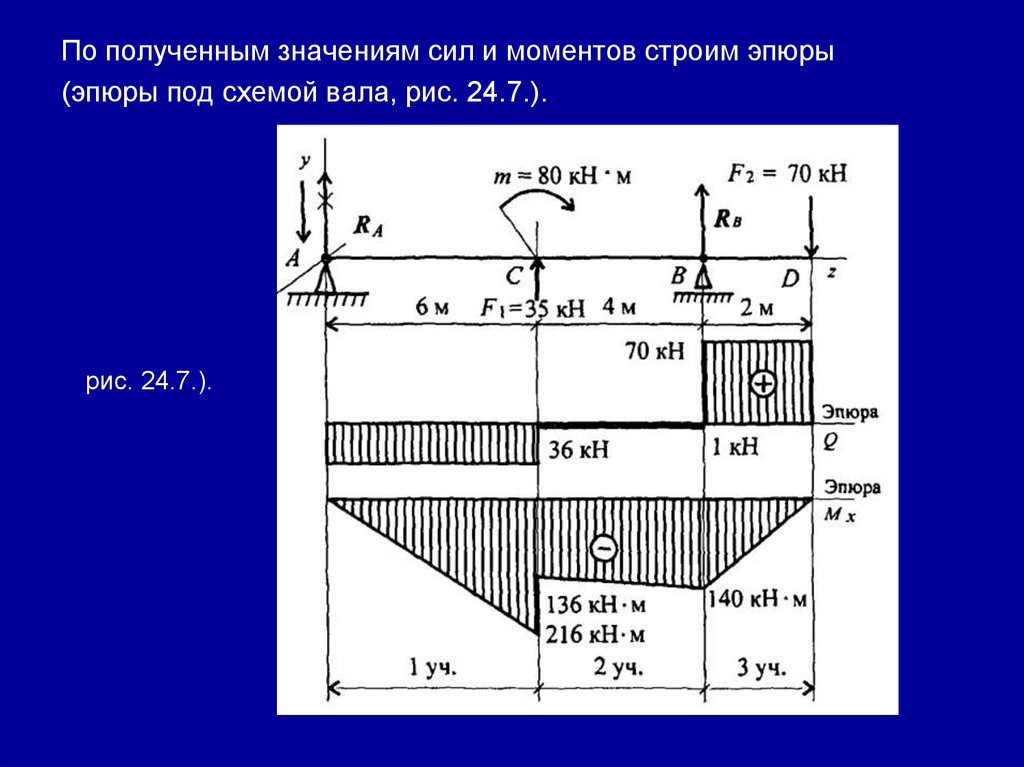




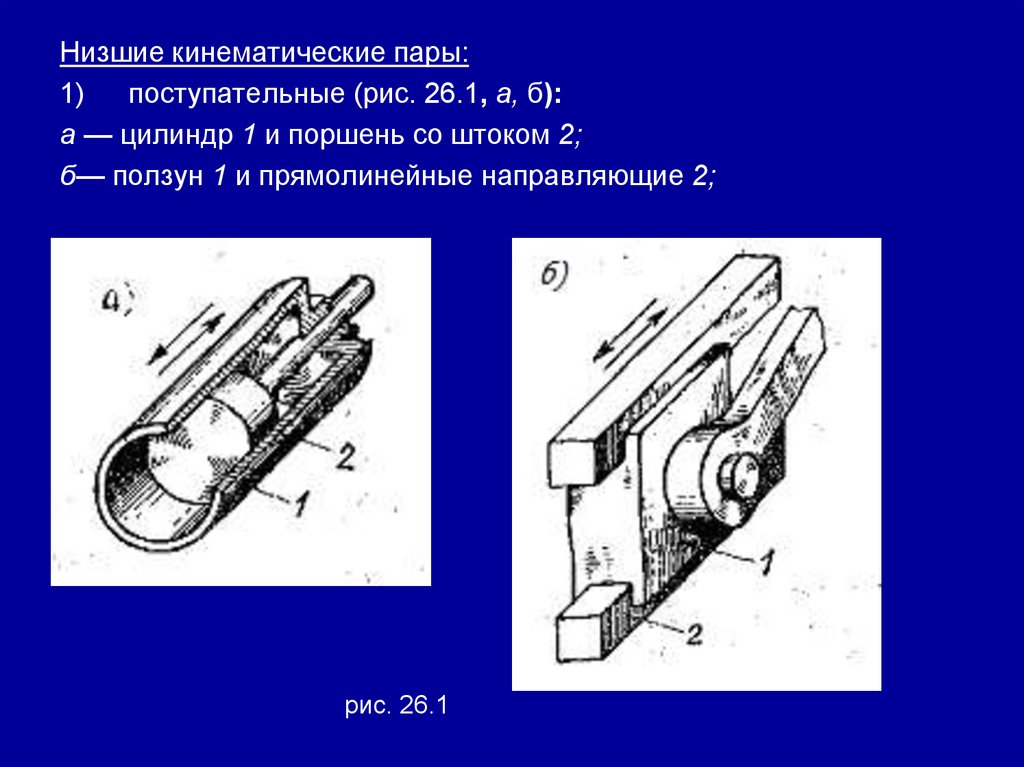
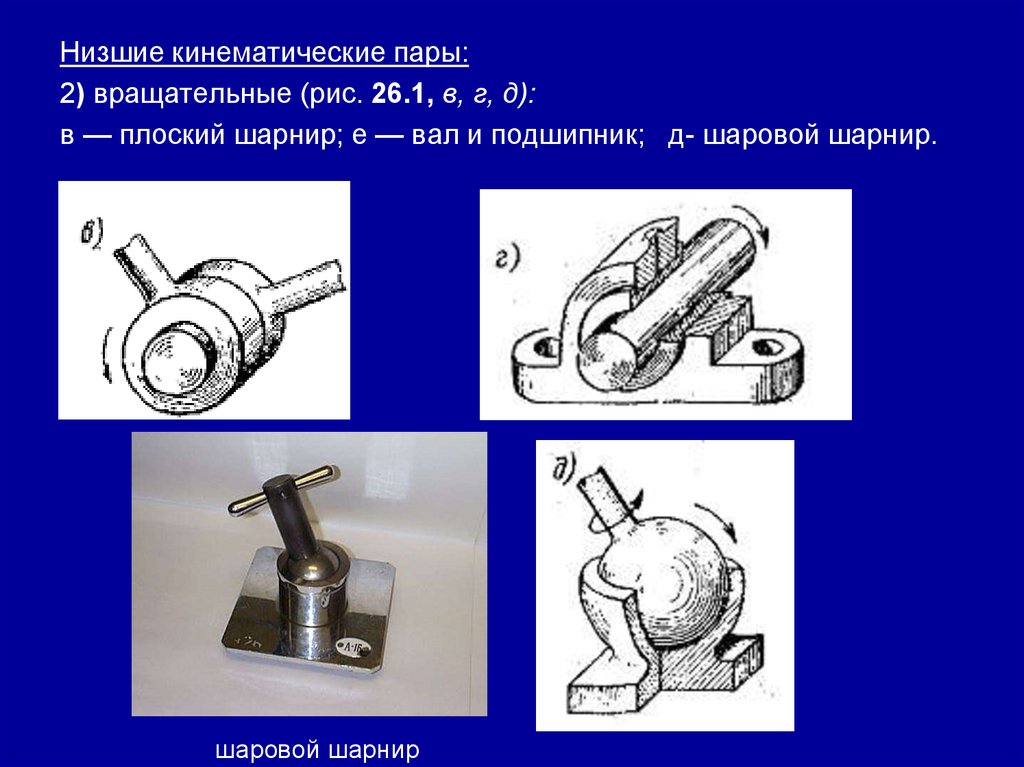


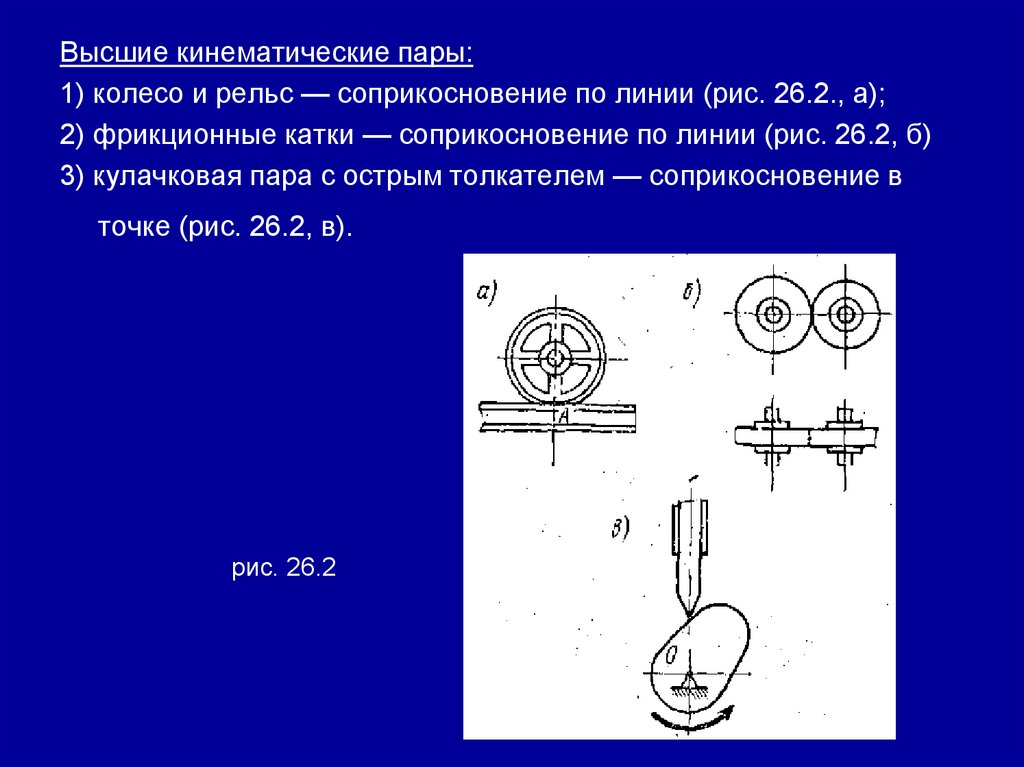



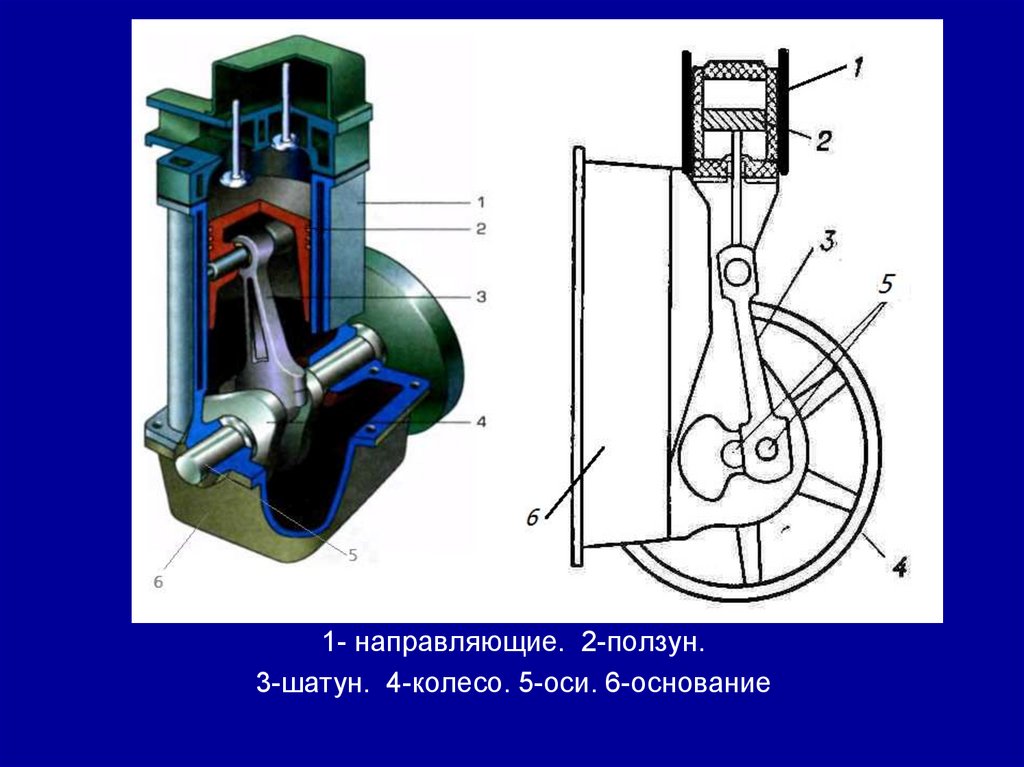

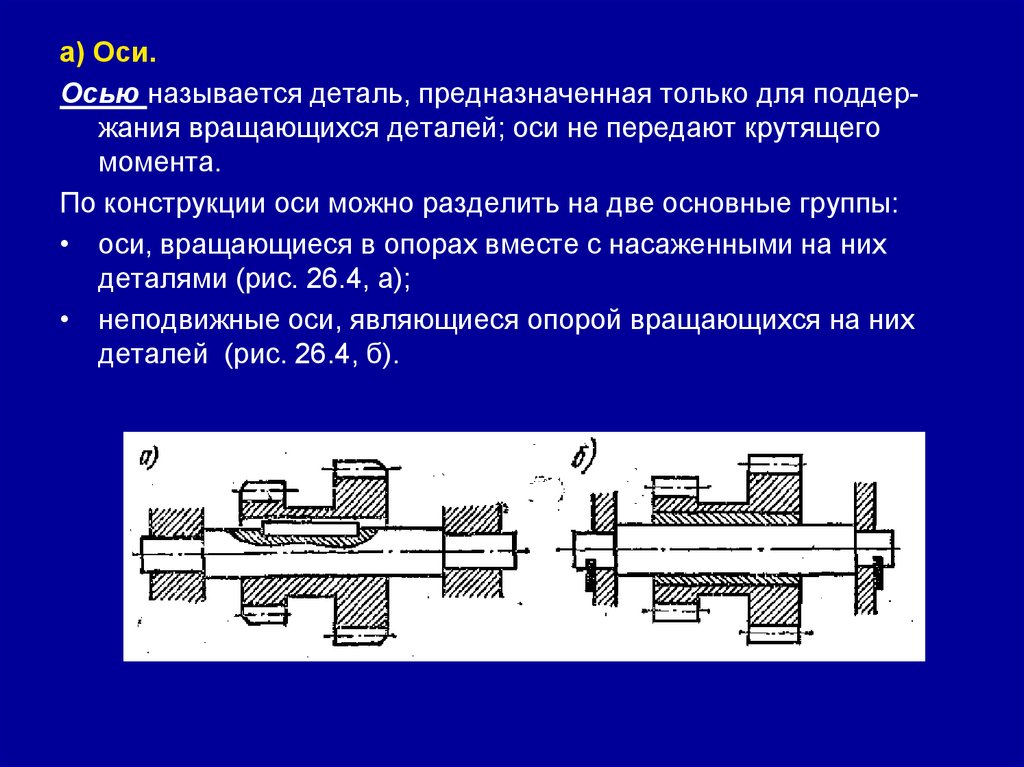



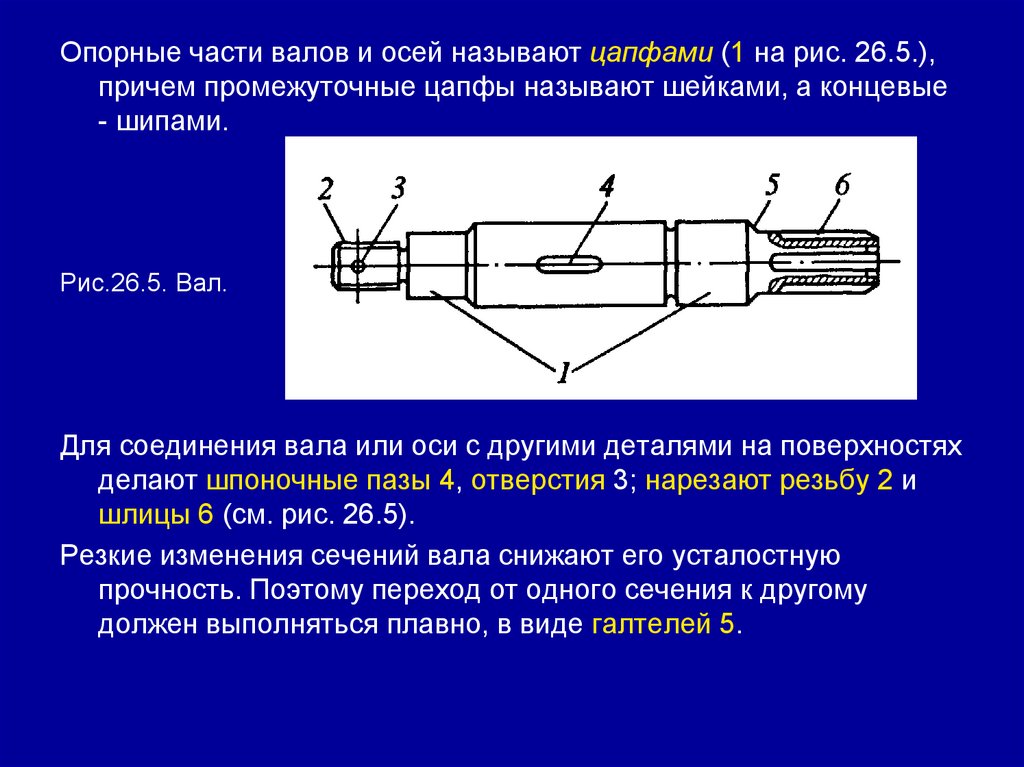






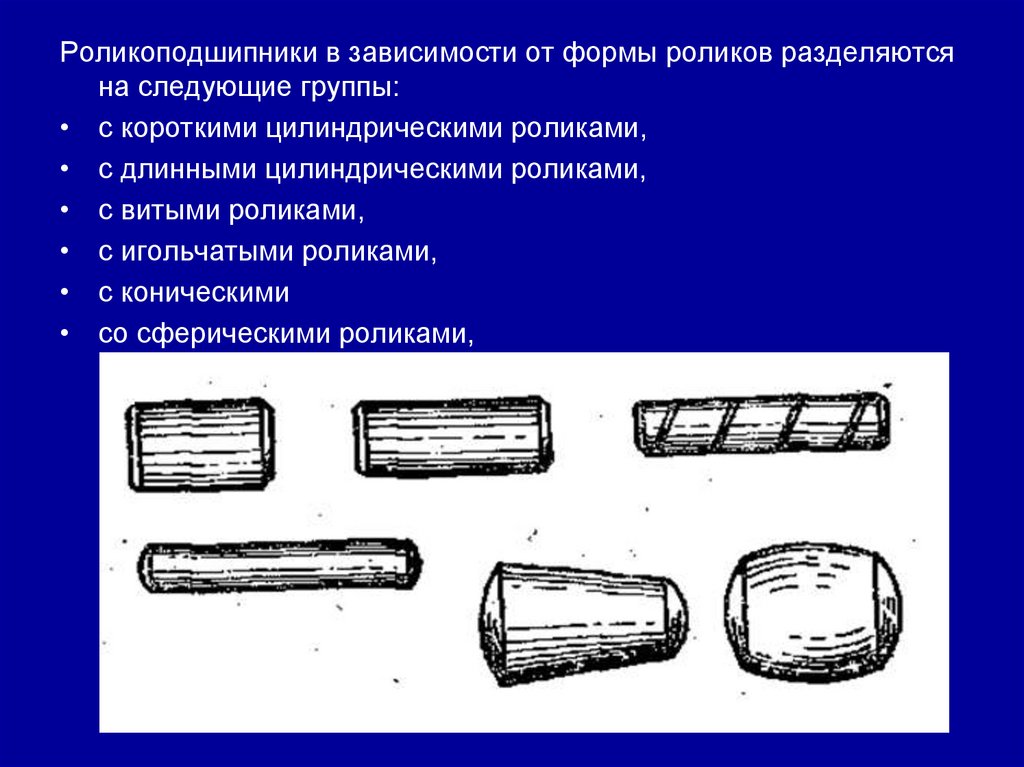
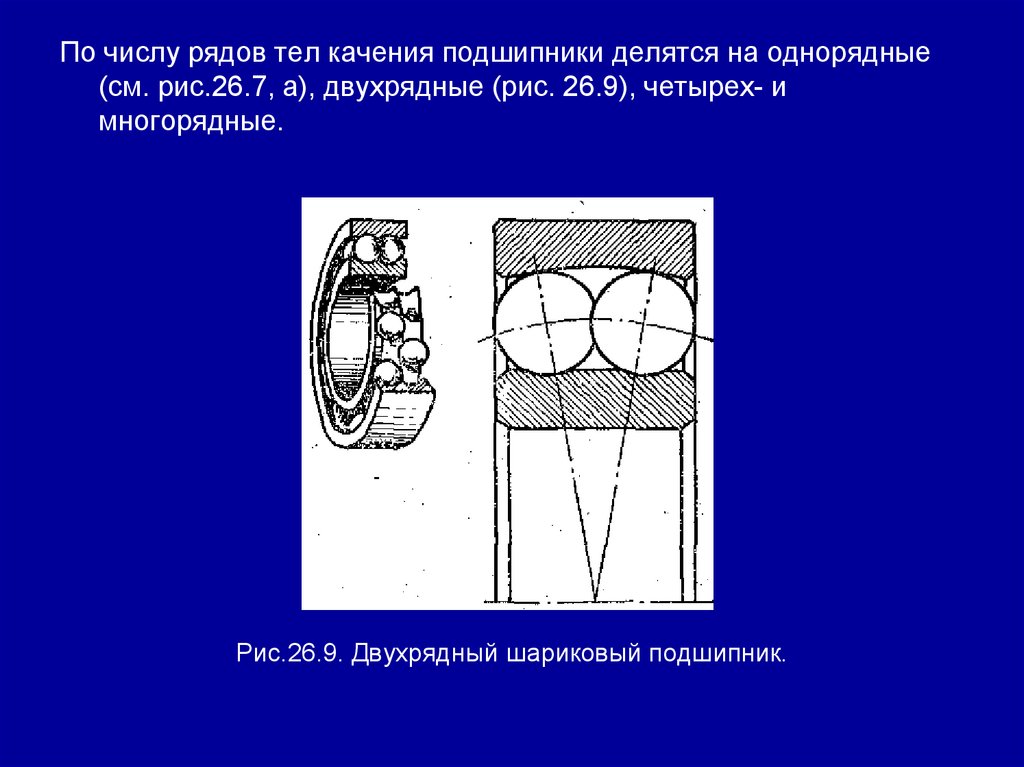






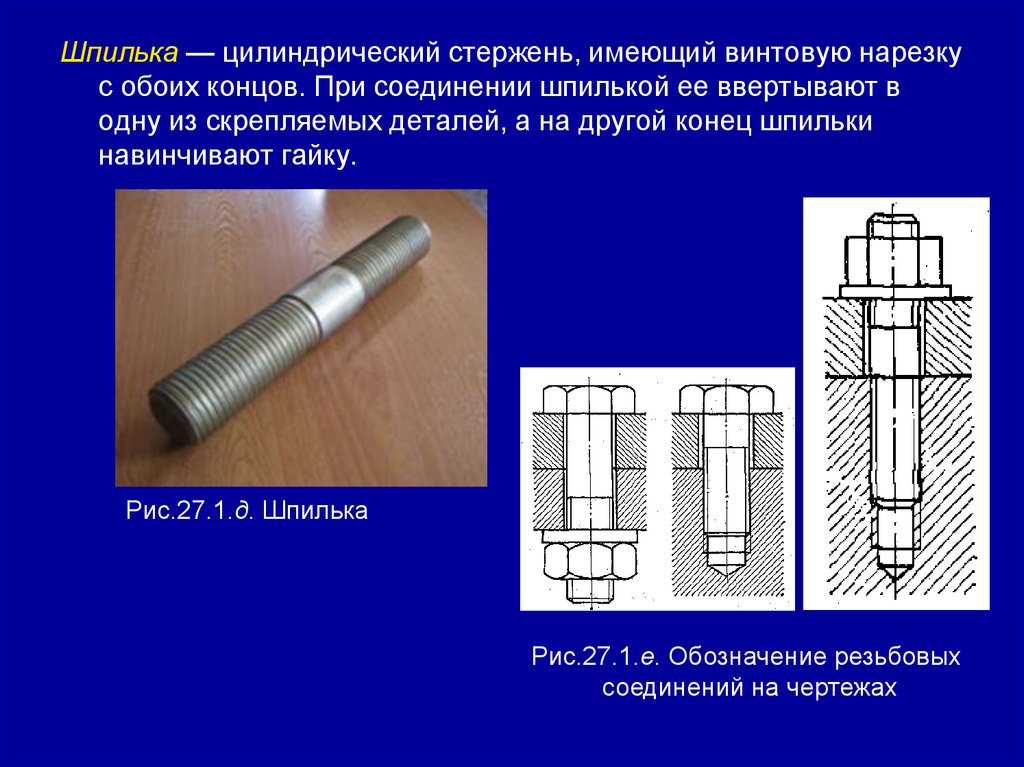
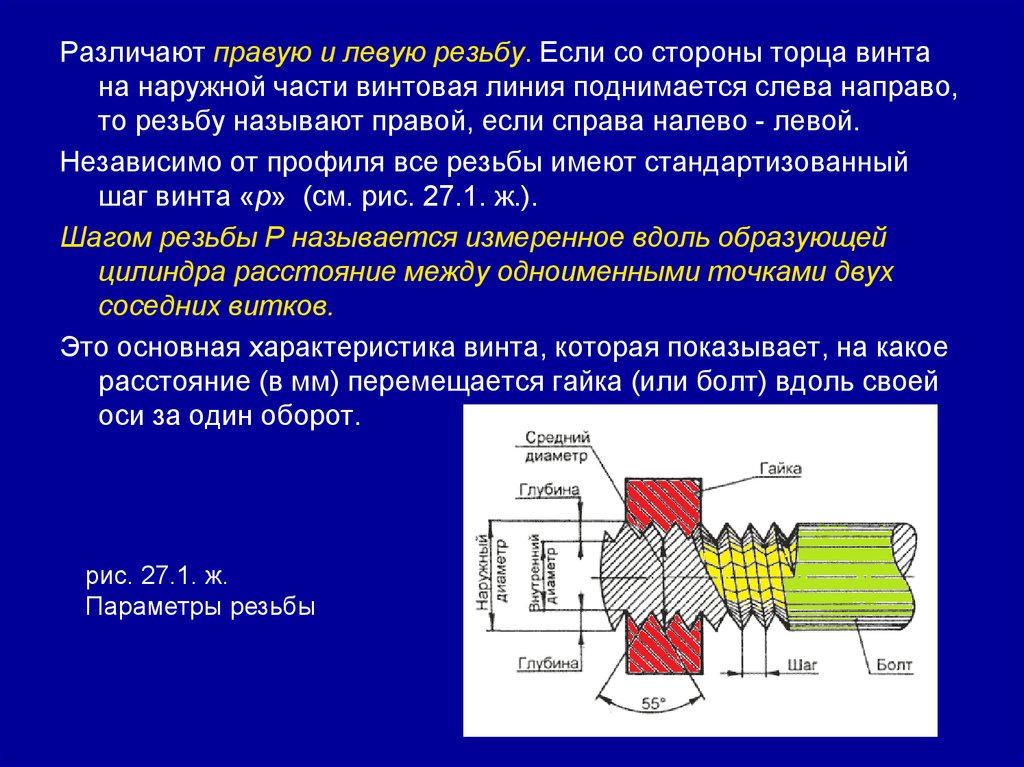




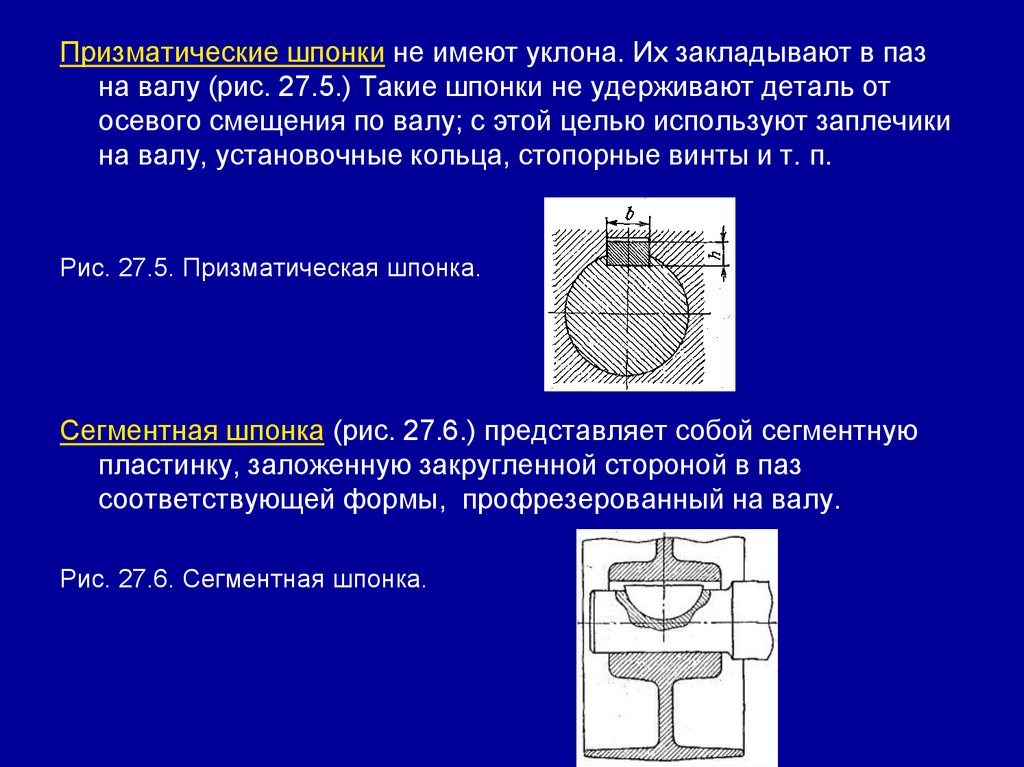


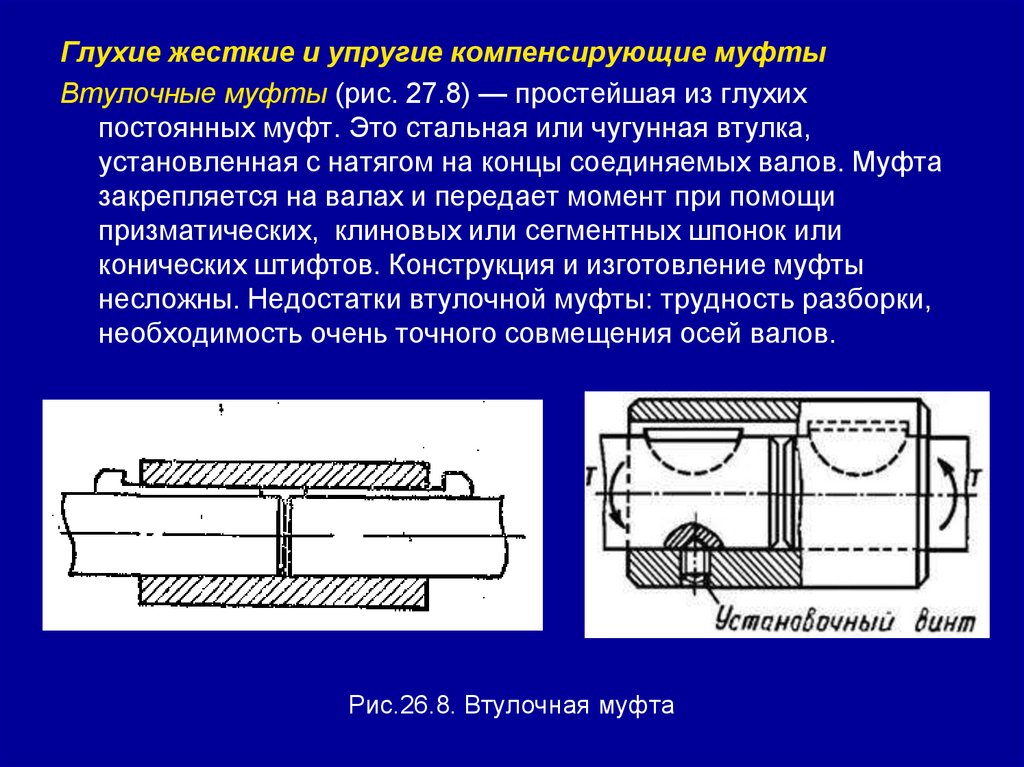
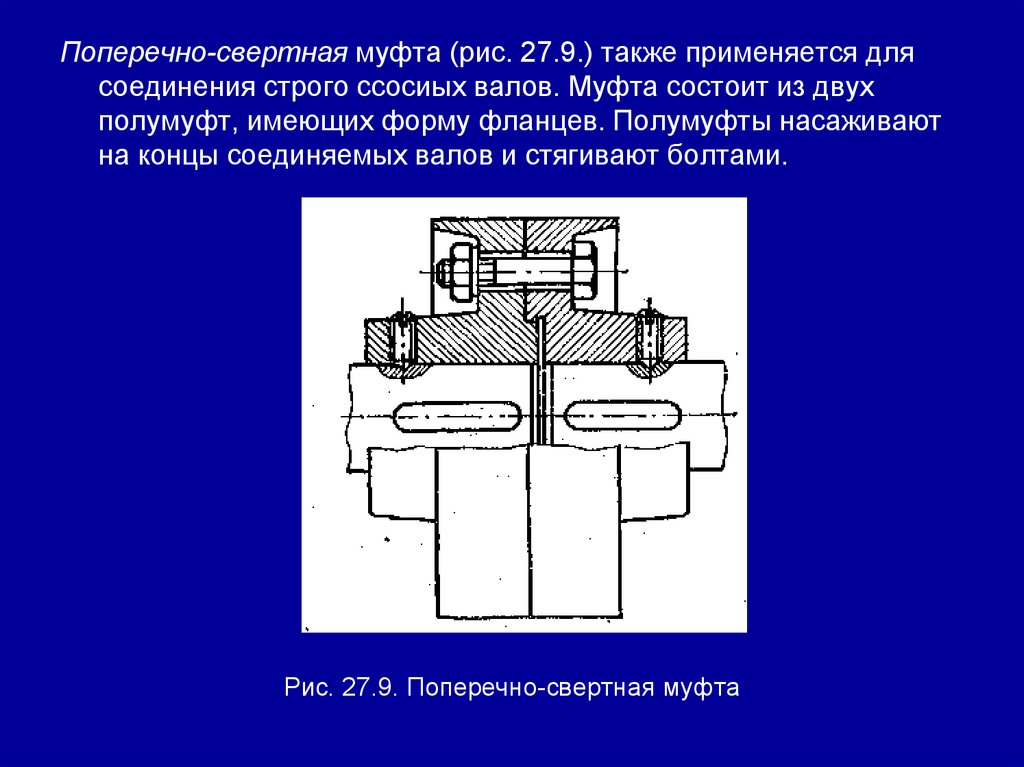
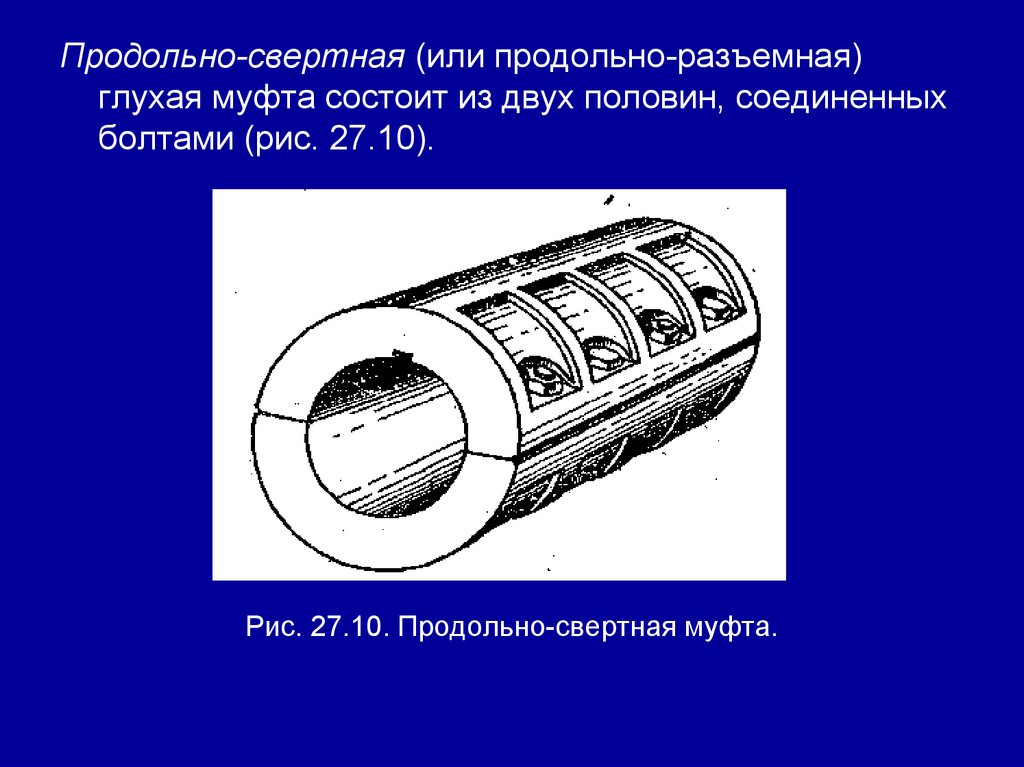
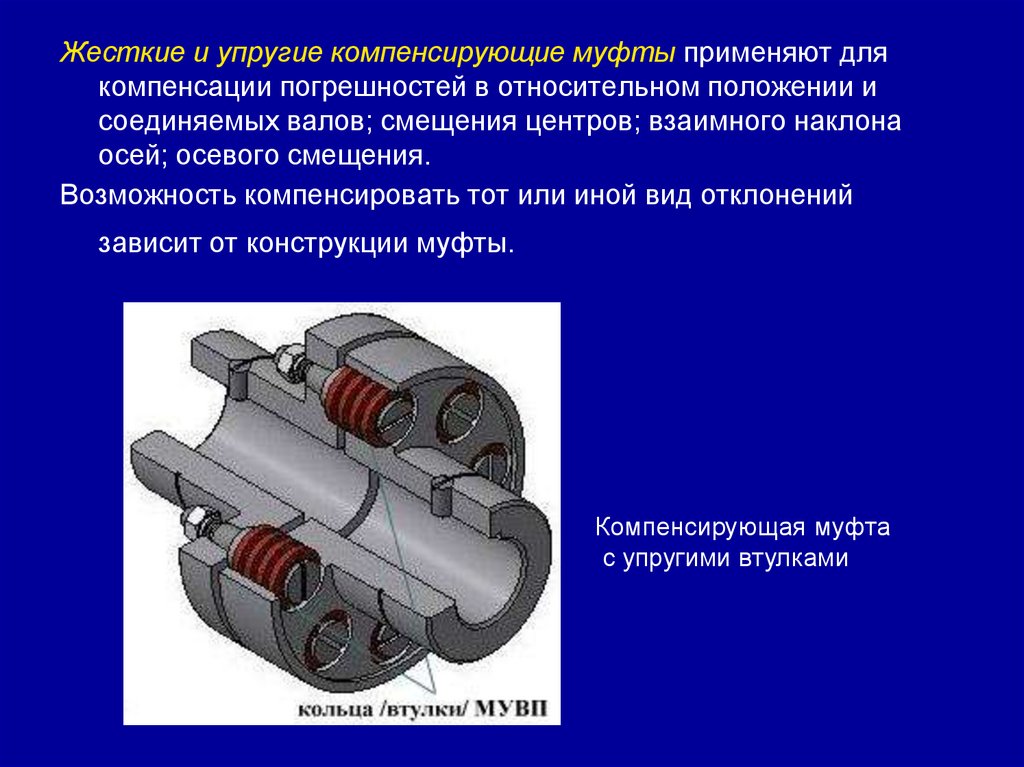



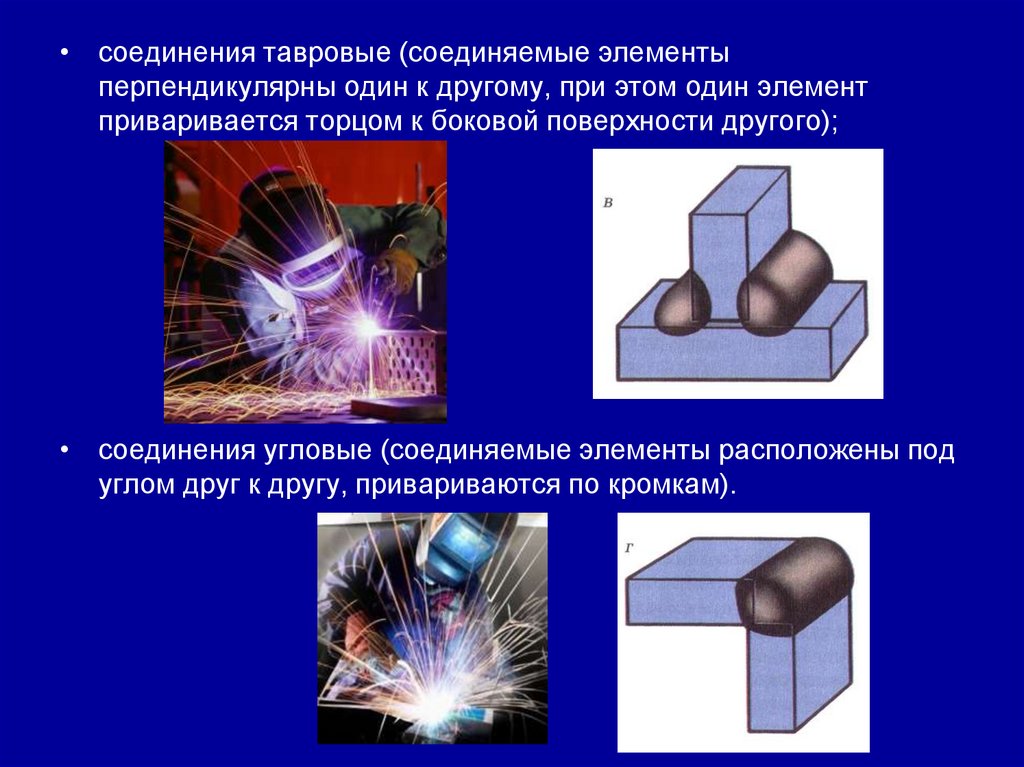
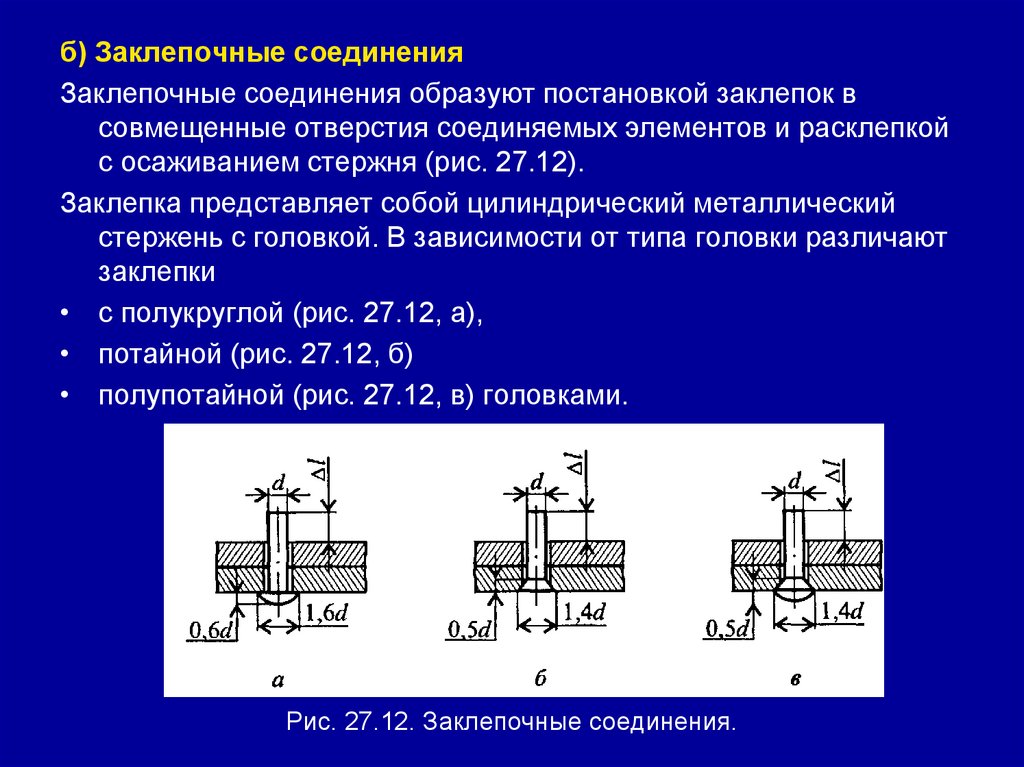










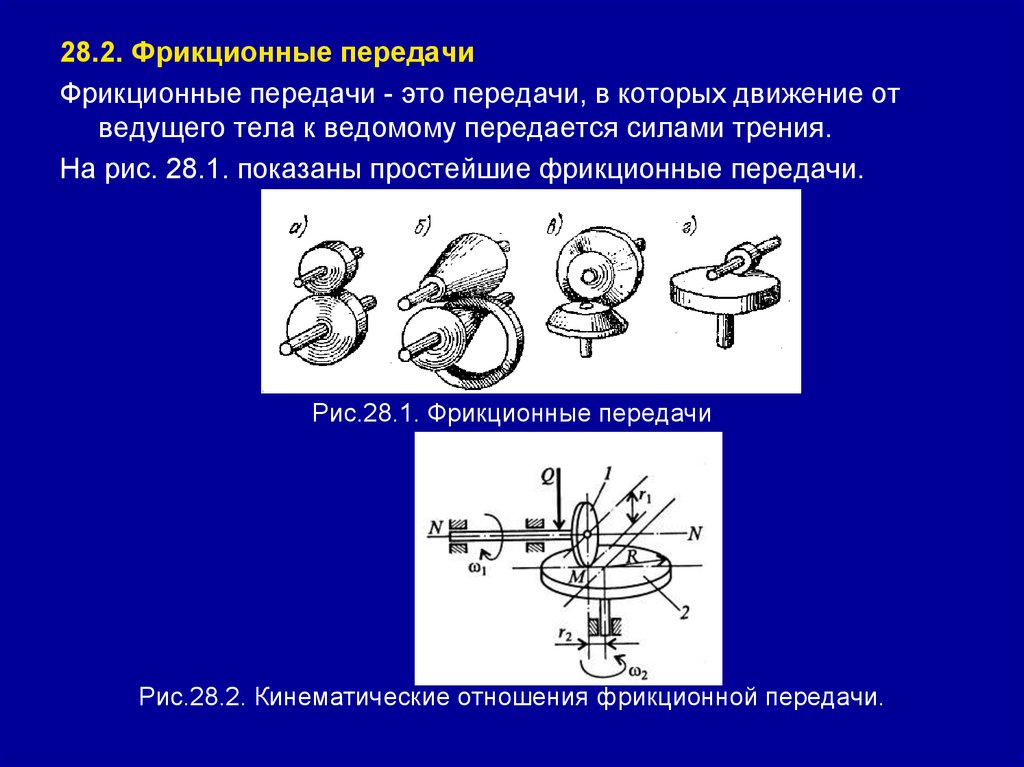
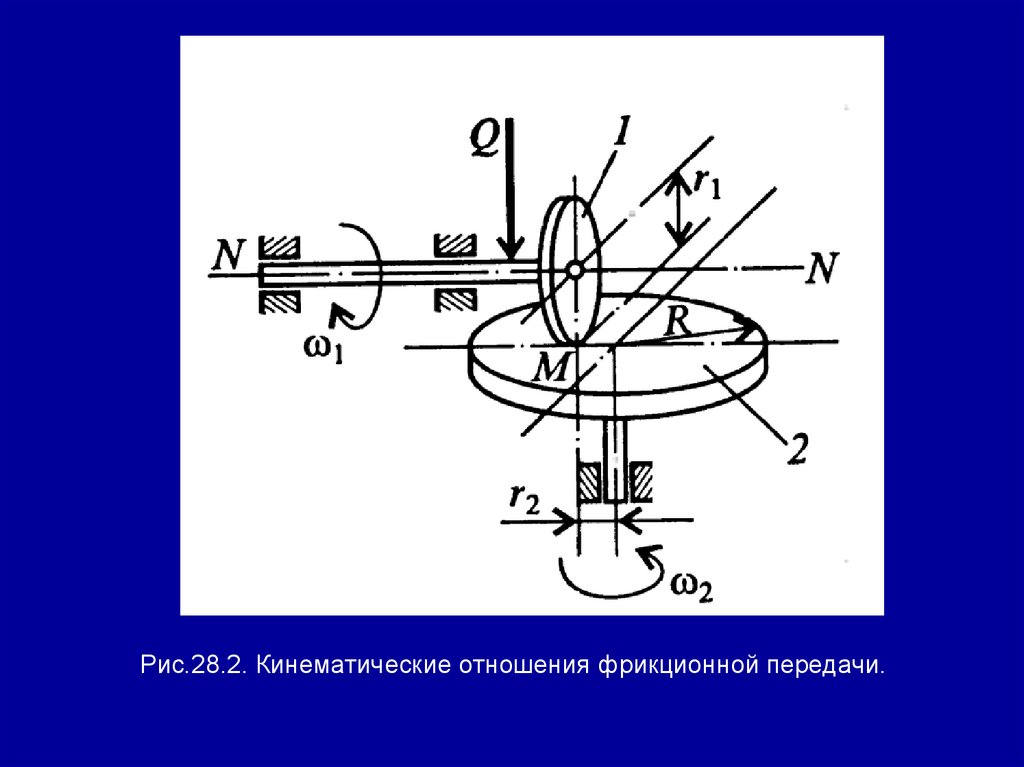


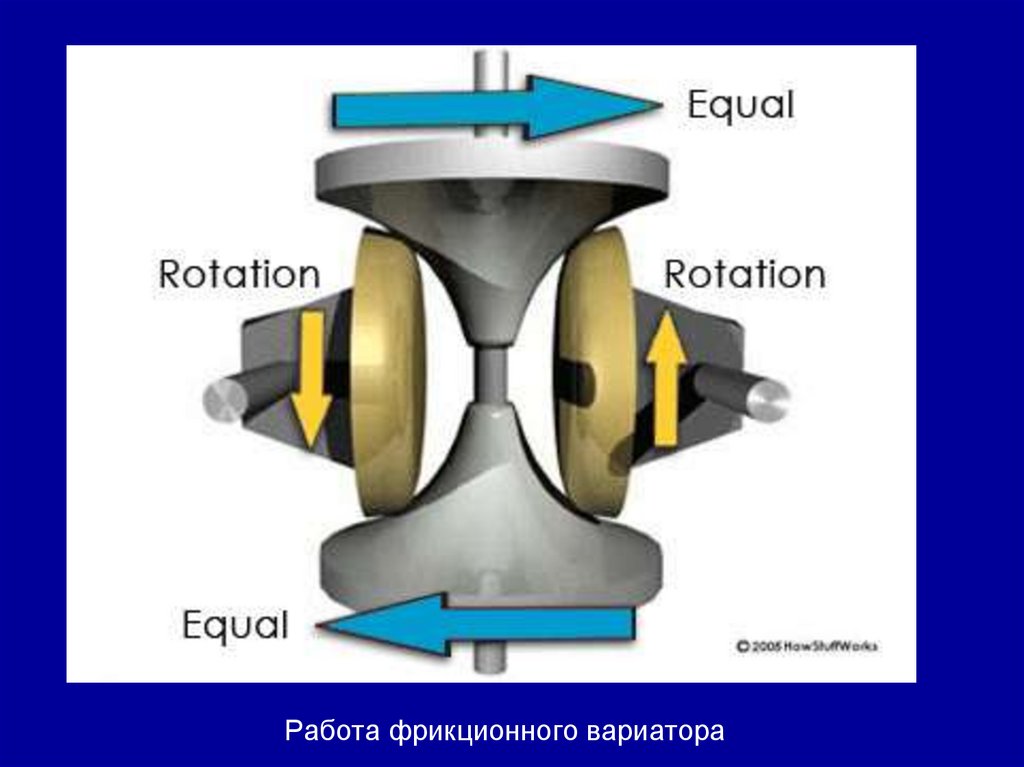

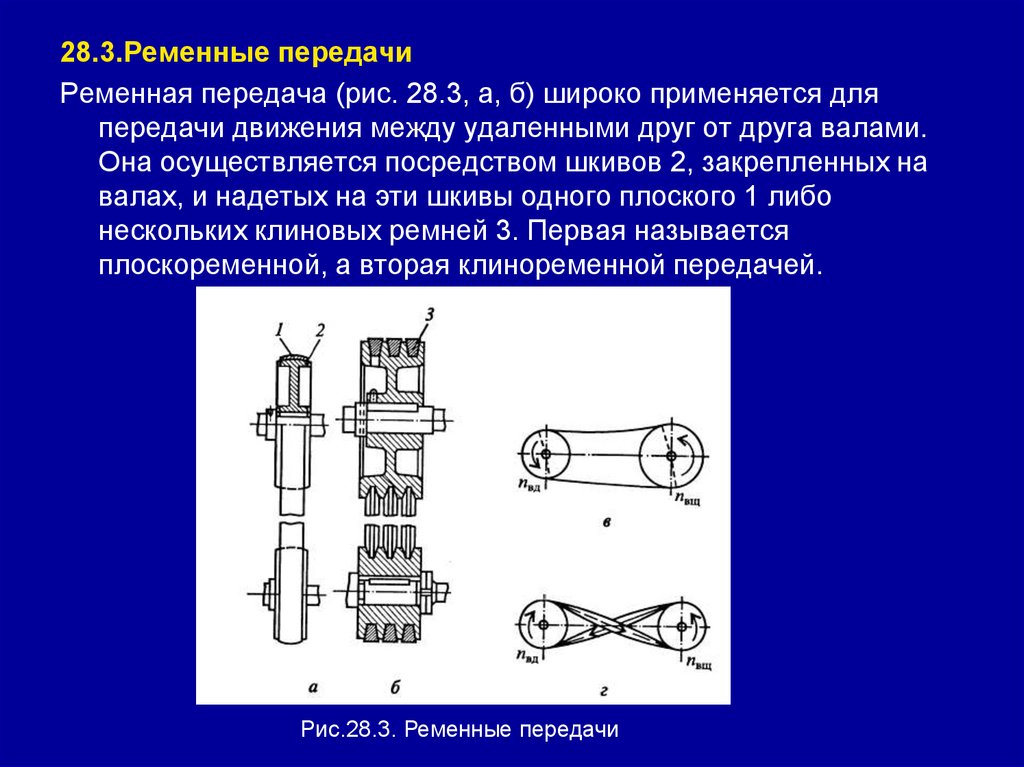




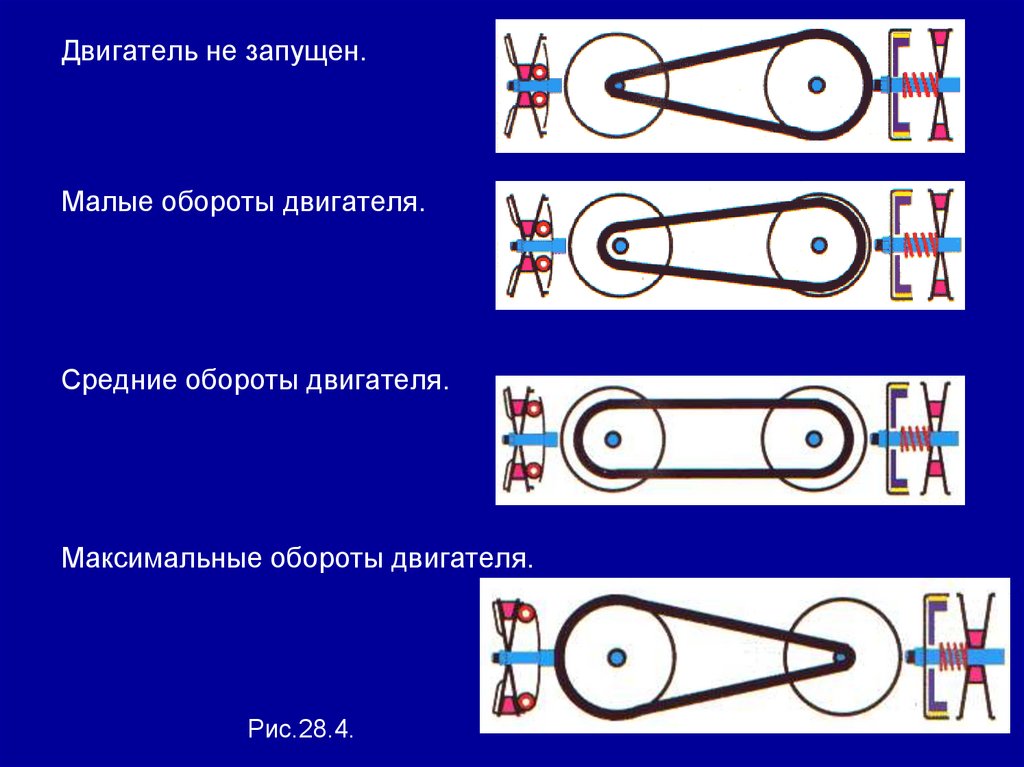


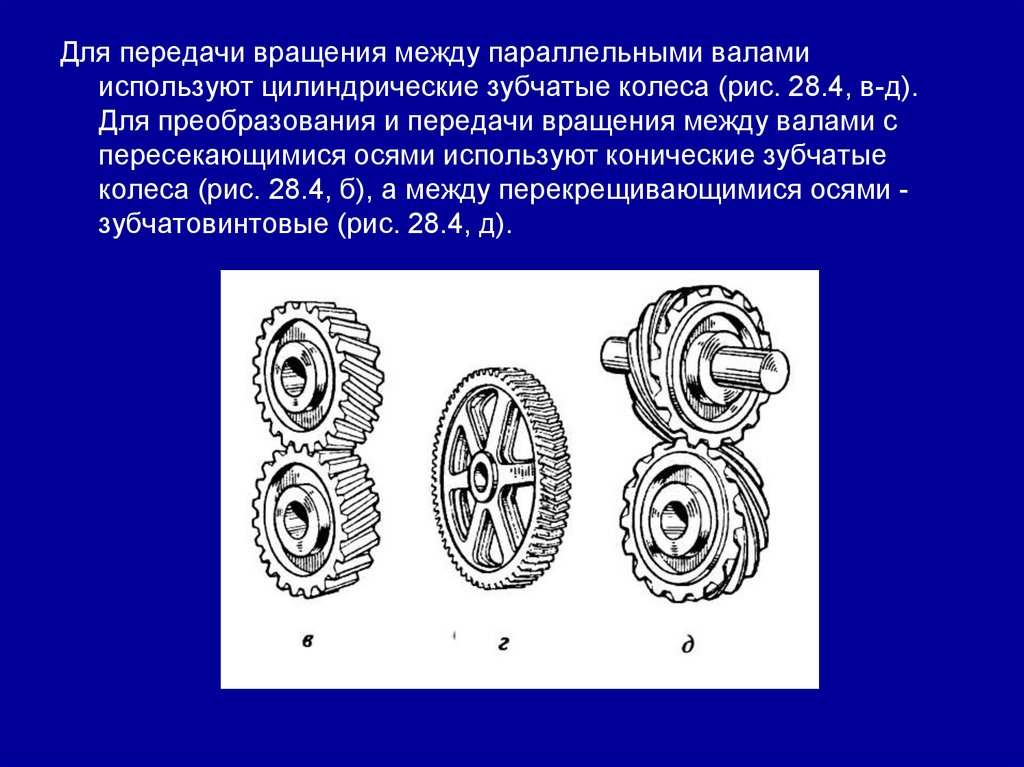













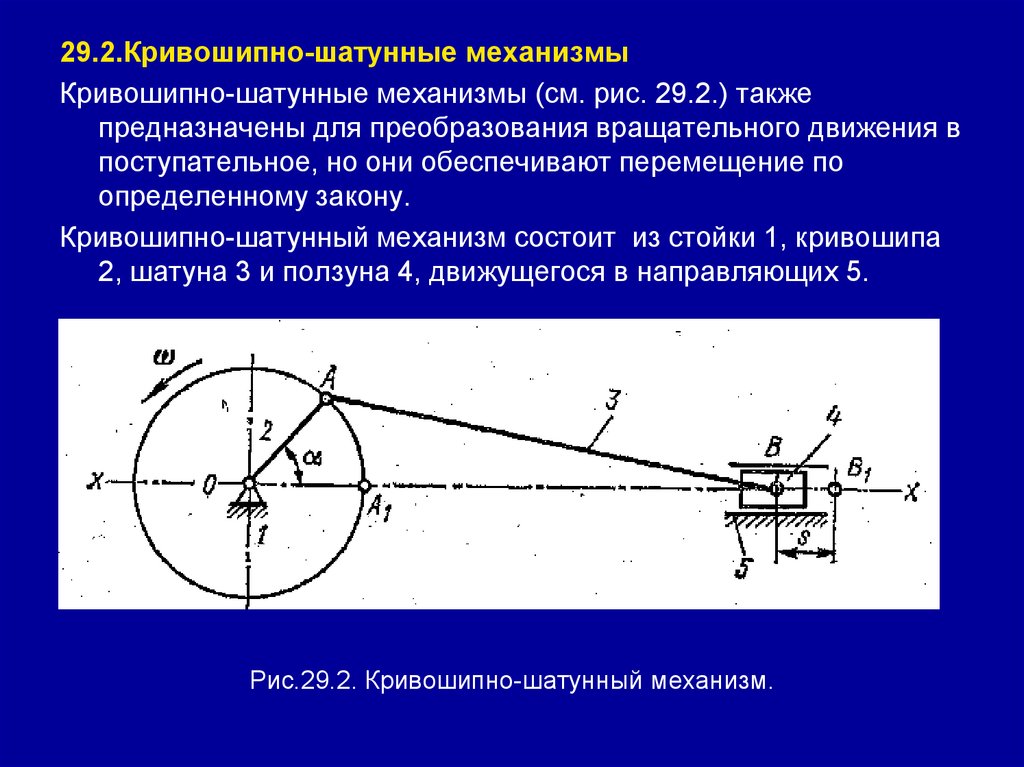


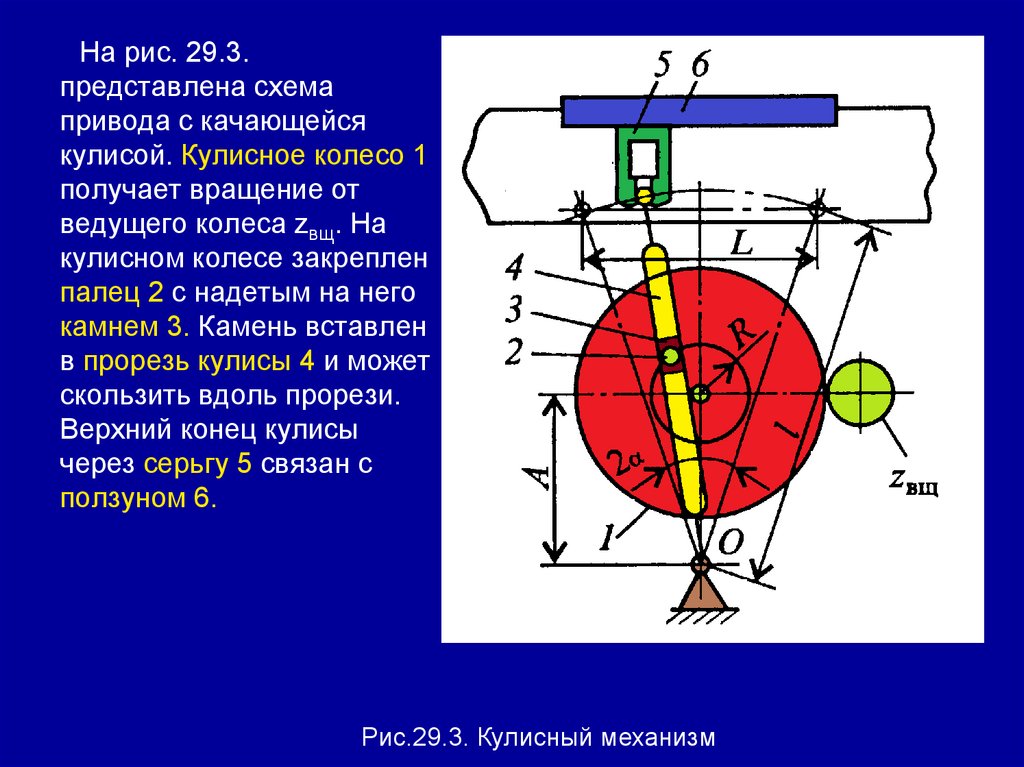

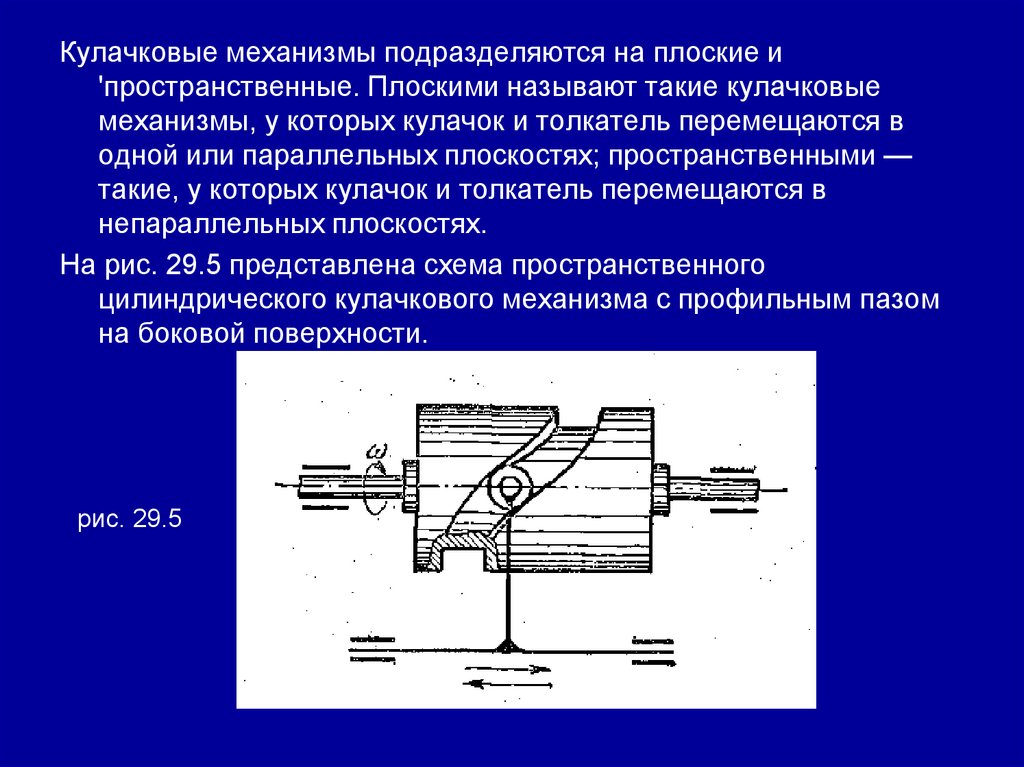
 Механика
Механика








