Похожие презентации:
Однородные тригонометрические уравнения
1. Однородные тригонометрические уравнения
*2.
*Однородноетригонометрическое уравнение это уравнение двух видов:
a sin x + b cos x = 0 (однородное
уравнение первой степени), либо
2
sin
2
cos
a
x + b sin x cos x + c
x=0
(однородное уравнение второй
степени)
3. Пример: Решим уравнение 2 sin x – 3 cos x = 0.
*Пример:Решим уравнение 2 sin x – 3 cos x = 0.
Алгоритм решения однородного уравнения
первой степени a sin x + b cos x = 0:
1) разделить обе части уравнения на cos x
2) решить получившееся уравнение
4.
•Пример: Решить уравнениеsin2 x – 3 sin x cos x + 2 cos2 x = 0
Делим обе части уравнения на cos2 x
sin
2.tg
cos
Получим, tg2 х - 3tgх + 2 = 0
Решаем квадратное уравнение относительно tgх
tgх = у, у2 – 3у + 2 = 0, Д = 1,у1 = 2, у2 = 2
Решаем теперь относительно х,
х1 = arctg 2 + Пn
х2 = arctg 1 + Пn
х2 = П/4 + Пn
5.
Решить самостоятельно*1.-sin2x + cos 2x - cos2x = 0
*2.sin2 x + sin x cos x = 0
*3.( sin x + cos x) 2 = cos2 x
*4. sin2x + 4 cos 2x = 1
*5. sin2x + 2cos 2x = 1
6.
Алгоритм решения однородного уравнениявторой степени
a sin2 x + b sin x cos x + c cos2 x = 0
*Условие: в уравнении должно быть
выражение вида a sin2 x.
Если его нет, то уравнение решается
методом разложения на множители.
1) Разделить обе части уравнения на cos2 x
2) Ввести новую переменную у,
заменяющую tg x (у = tg x)
3) Решить получившееся уравнение
7.
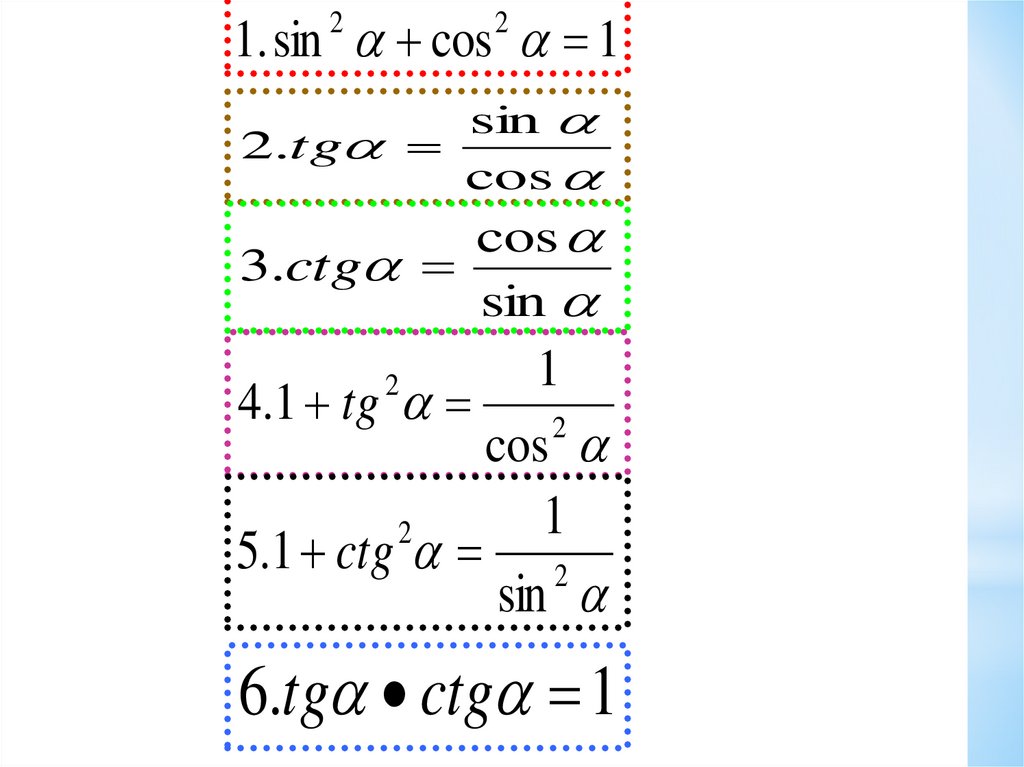
1. sin cos 12
2
sin
2.tg
cos
cos
3.ctg
sin
1
4.1 tg
2
cos
2
1
5.1 ctg 2
sin
2
6.tg ctg 1
*
8.
7. sin 2 2 sin cos8. cos 2 cos sin
2
2tg
9.tg 2
2
1 tg
2
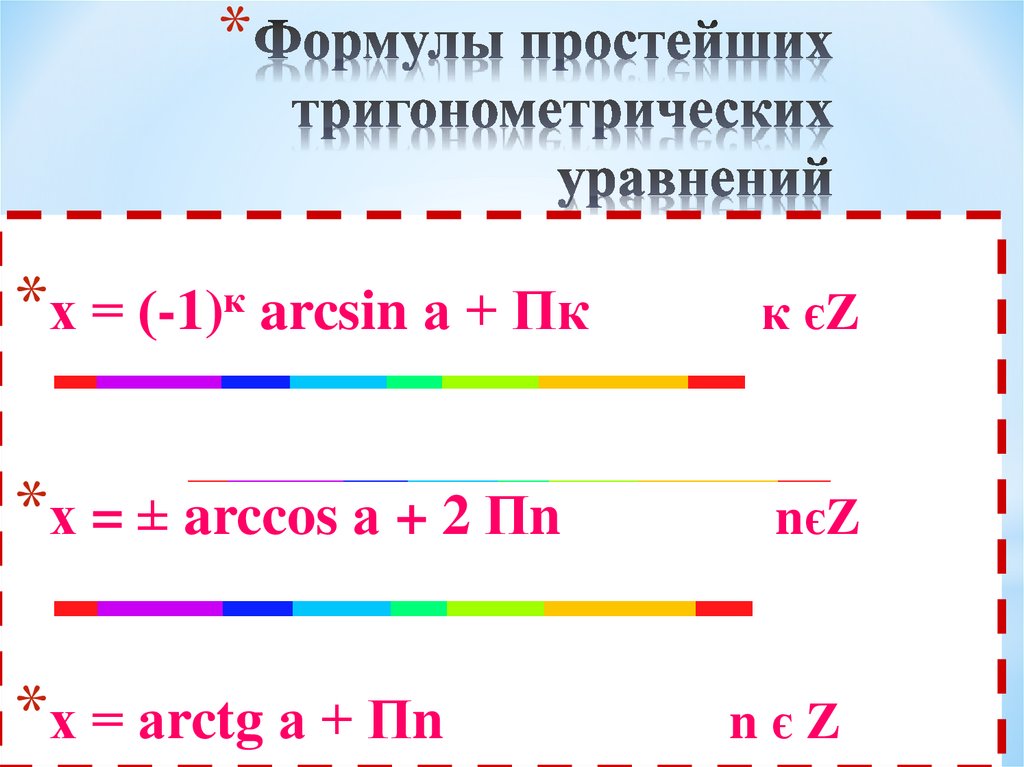
9. Формулы простейших тригонометрических уравнений
**х = (-1)к arcsin а + Пк
к єZ
*х = ± arccos а + 2 Пn
nєZ
*х = аrctg а + Пn
nєZ
10. Особые случаи для синуса
а о, х Пn;П
а 1, х
2 Пn;
2
П
а 1, х
2 Пn.
2
*
11. Особые случаи для косинуса
Па о, х
Пn
2
а 1, х П 2 Пn
а 1, х 2 Пn
*






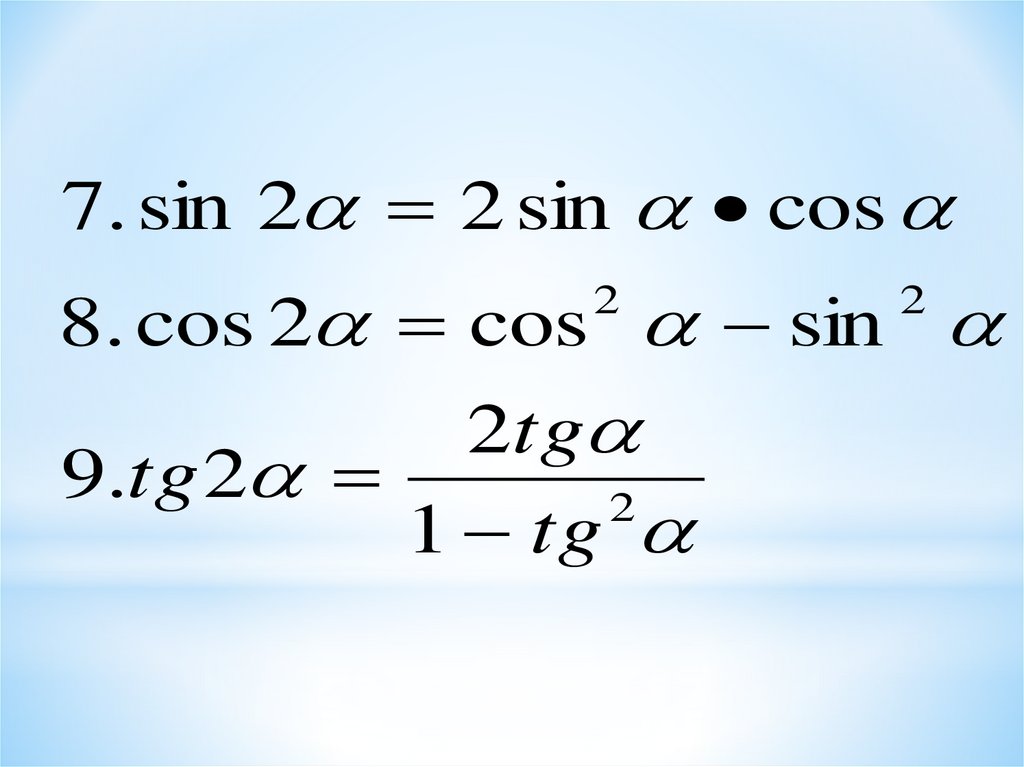


 Математика
Математика








