Похожие презентации:
Дифференцирование показательной и логарифмической функции
1. Дифференцирование показательной и логарифмической функции
Алгебра и начала математического анализаДифференцирование
показательной и
логарифмической функции
.
2.
Число е. Функция y = ex, еёсвойства, график,
дифференцирование
3.
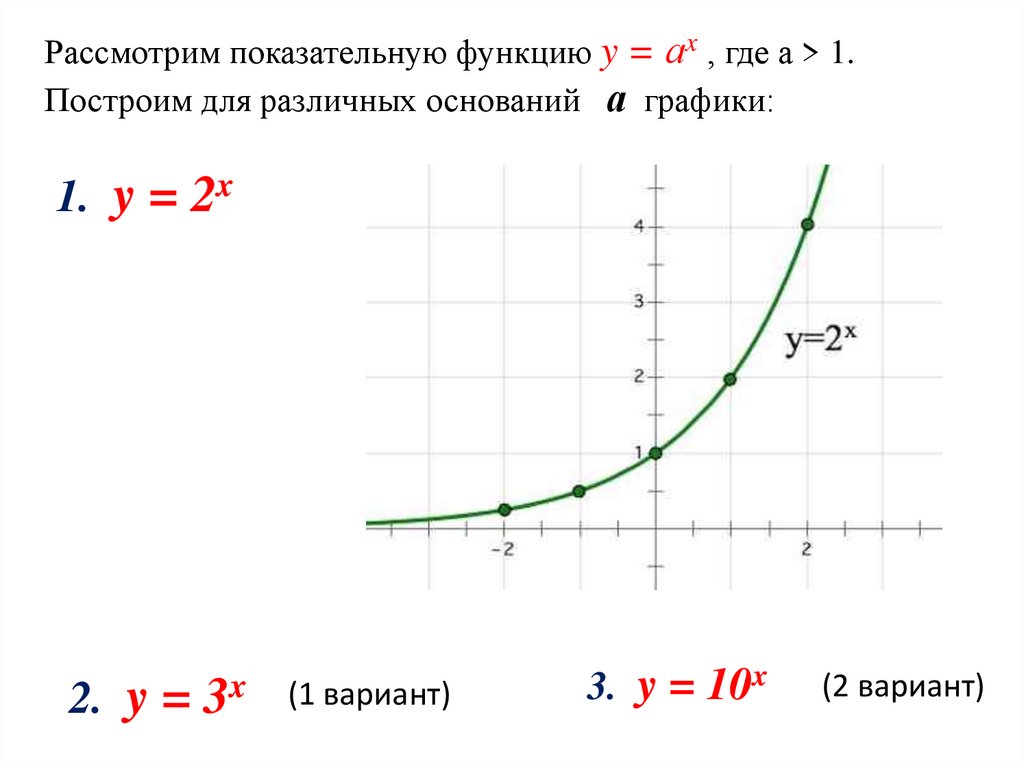
Рассмотрим показательную функцию y = аx , где а > 1.Построим для различных оснований а графики:
1. y = 2x
2. y =
3x
(1 вариант)
3. y = 10x
(2 вариант)
4.
1)Все графики проходят через точку (0 ; 1);2) Все графики имеют горизонтальную асимптоту у = 0
при х ∞;
3) Все они обращены выпуклостью вниз;
4) Все они имеют касательные во всех своих точках.
5.
Проведем касательную к графику функции y = 2xв точке х = 0 и измерим угол , который образует касательная
с осью х
350
6.
7.
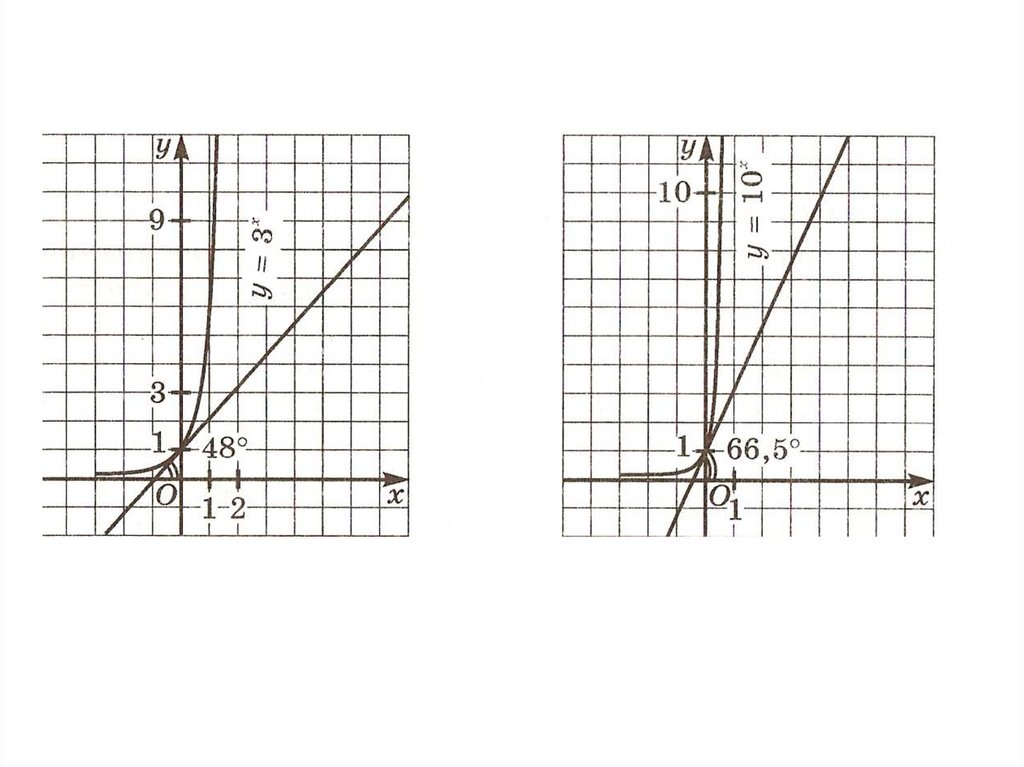
С помощью точных построений касательных к графикамможно заметить, что если основание а показательной
функции y = аx постепенно увеличивается основание от 2
до 10, то угол между касательной к графику функции в
точке х = 0 и осью абсцисс постепенно увеличивается от
35’ до 66,5’.
Следовательно существует основание а, для которого
соответствующий угол равен 45’. И это значение а
заключено между 2 и 3, т.к. при а = 2 угол равен 35’, при а
= 3 он равен 48’.
В курсе математического анализа доказано, что данное
основание существует, его принято обозначать буквой е.
Установлено, что е – иррациональное число, т. е.
представляет собой бесконечную непериодическую
десятичную дробь:
е = 2, 7182818284590… ;
На практике обычно полагают, что е ≈ 2,7.
8.
9. График и свойства функции y = еx :
1) D (f) = ( - ∞; + ∞ );2) не является ни четной, ни
нечетной;
3) возрастает;
4) не ограничена сверху, ограничена
снизу
5) не имеет ни наибольшего, ни
наименьшего
значения;
6) непрерывна;
7) E (f) = ( 0; + ∞ );
8) выпукла вниз;
9) дифференцируема.
Функцию y = еx
называют экспонентой.
10.
В курсе математического анализа доказано,что функция y = еx имеет производную в
любой точке х:
x
(e )
=
x
e
(е5х)' = 5е5х
(ех-3)' = ех-3
(е-4х+1)' = -4е-4х-1
11.
Пример 1. Провести касательную к графикуфункции y e x в точке x=1.
Решение:
y f ( х0 ) f ( х0 )( x х0 )
1) х0 =1
2) f( х0 )=f(1)=e
3)
x
f ( x) e ; f ( х0 ) f (1) e.
4) y=e+e(x-1);
y = ex
Ответ:
y=ex
12.
Пример 2.Вычислить значение производной функции
в точке x = 3.
Решение
(самостоятельно) :
Ответ:
y e 4 x 12
13.
Пример 3.Исследовать на экстремум функцию
Решение:
1)
2)
y x e
2
x
14.
3)4)
Ответ:
15.
Натуральные логарифмы.Функция y = ln x, её свойства,
график, дифференцирование
16.
Если основанием логарифма служит число е, тоговорят, что задан натуральный логарифм. Для
натуральных логарифмов введено специальное
обозначение ln (l – логарифм, n – натуральный).
log e 2 ln 2
ln x log e x
ln1 0;
ln е 1;
ln е r;
r
log e 7 ln 7
x;
ln x
log a x
.
ln a
е
ln x
17. График и свойства функции y = ln x
Свойства функции y = ln x:1) D (f) = ( 0; + ∞);
2) не является ни четной, ни
нечетной;
3) возрастает на ( 0; + ∞);
4) не ограничена;
5) не имеет ни наибольшего, ни
наименьшего значений;
6) непрерывна;
7) Е (f) = ( - ∞; + ∞ );
8) выпукла верх;
9) дифференцируема.
18.
В курсе математического анализа доказано, чтодля любого значения х>0 справедлива
формула дифференцирования
1
ln x
x
19.
Пример 4:Вычислить значение производной функции
в точке x = -1.
y ln 3x 5
Решение:
y ' ln 3 x 5
1
3
3
;
3x 5 3x 5
3
f ' 1
1,5.
3 ( 1) 5
Ответ: 1,5
20.
y aДифференцирование функции
x
a e
x
x ln a
a e
x
x ln a
x ln a
x
(a ) (e ) ln a e
ln a a
ln a
(a ) a ln a
x
Например:
5
3 x
2
x
x
2 ln 2;
x
3 5 3 x ln 5.
4
x 5
4
x 5
ln 4.
21.
Дифференцирование функцииy log a x
ln x
1
y (log a x)
ln x
ln a
ln a
1
1 1
x ln a
ln a x
1
(log a x)
x ln a
22.
(e ) ' ex
x
(a ) a ln a
x
x
1
ln x
x
1
(log a x)
x ln a




















 Математика
Математика








