Построение графиков функций , содержащих модуль

1.

Министерство науки и высшего образования Российской Федерации Федеральное
государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет »
(ФГБОУ ВО «ВГТУ», ВГТУ)
Структурное подразделение : Строительно-политехнический колледж .
Исследовательский проект
«Построение графиков функций , содержащих модуль
Выполнил: студент 1 курса группы
ЗИО-201о
Куликов Кирилл Русланович
Руководитель:
Рыбина Светлана Леонидовна
Воронеж 2021

2.

Анкетирование
После того, как я провёл опрос среди
студентов моей группы, я пришёл к выводу,
что строить графики функций с модулем
могут немногие. А именно: среди студентов
группы “Зио201-о“ всего 2 человека из 25
могут строить графики функций со знаком
модуля.
Теперь мы можем сделать вывод, что
графиков функций с модулем большое
разнообразие, и каждый человек должен знать
самые основные, а тем, кто интересуется
графиками, будет интересно рассмотреть
примеры более трудных.
Умеют
Не умеют

3.

График Функции и Модуль
Определение графика функции. Графиком
функции называется совокупность всех точек
плоскости, прямоугольные координаты которых х и
у удовлетворяют уравнению у = f (х).
Горизонтальную ось Ох называют осью абсцисс ,
вертикальную ось Оу – осью ординат.
Модуль числа a -или абсолютная величина числа a
равна a, если a больше или равно нулю и равна -a, если
a меньше нуля:
Из определения следует, что для любого
действительного числа a,

4.

График функции у =f(х)
Графиком функции у=f(х),где x∈R , называется
множество всех точек координатной плоскости хОу или
графиком функции называется множество всех точек,
абсциссы которых равны значениям аргумента, а
ординаты – соответствующим значениям функции.
Важные точки графика функции y = f(x):
стационарные и критические точки ;
точки экстремума;
нули функции;
точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна
нулю.
Критические точки — точки, в которых производная функции f(x) равна
нулю либо не существует . Стационарные точки являются подмножеством
множества критических точек.
Экстремум в математике — максимальное или минимальное значение
функции на заданном множестве . Точка, в которой достигается экстремум,
называется точкой экстремума. Соответственно , если достигается минимум
— точка экстремума называется точкой минимума , а если максимум —
точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.

5.

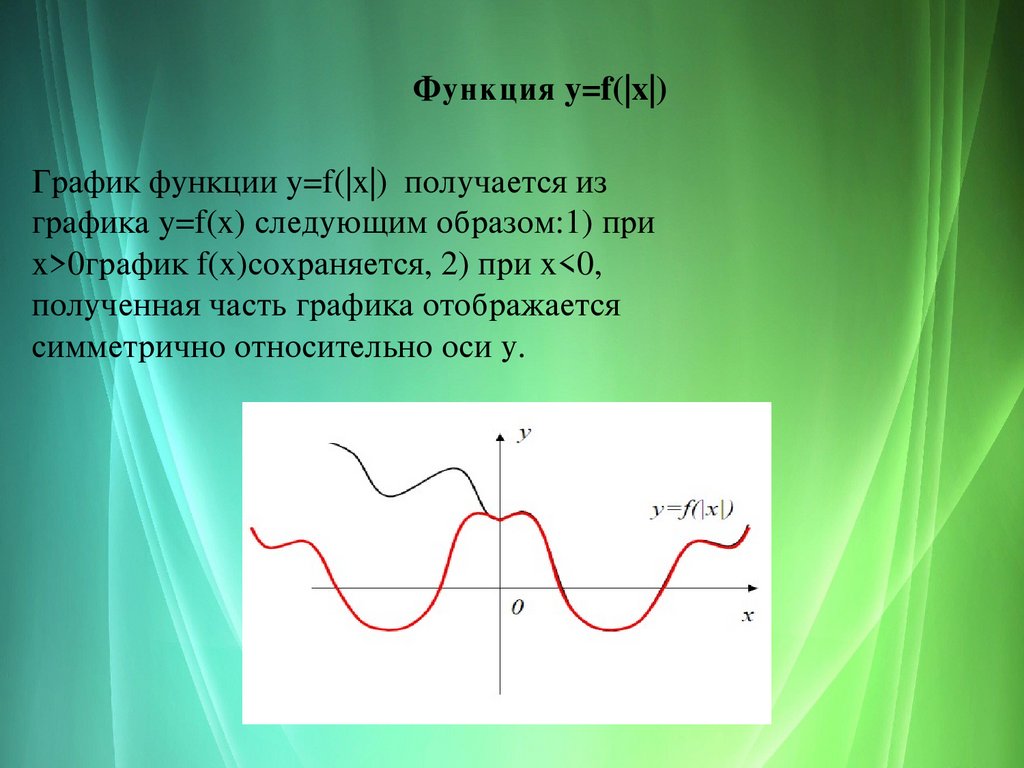
Функция y=f(|x|)
График функции y=f(|x|) получается из
графика y=f(x) следующим образом:1) при
х>0график f(x)сохраняется, 2) при x<0,
полученная часть графика отображается
симметрично относительно оси у.

6.

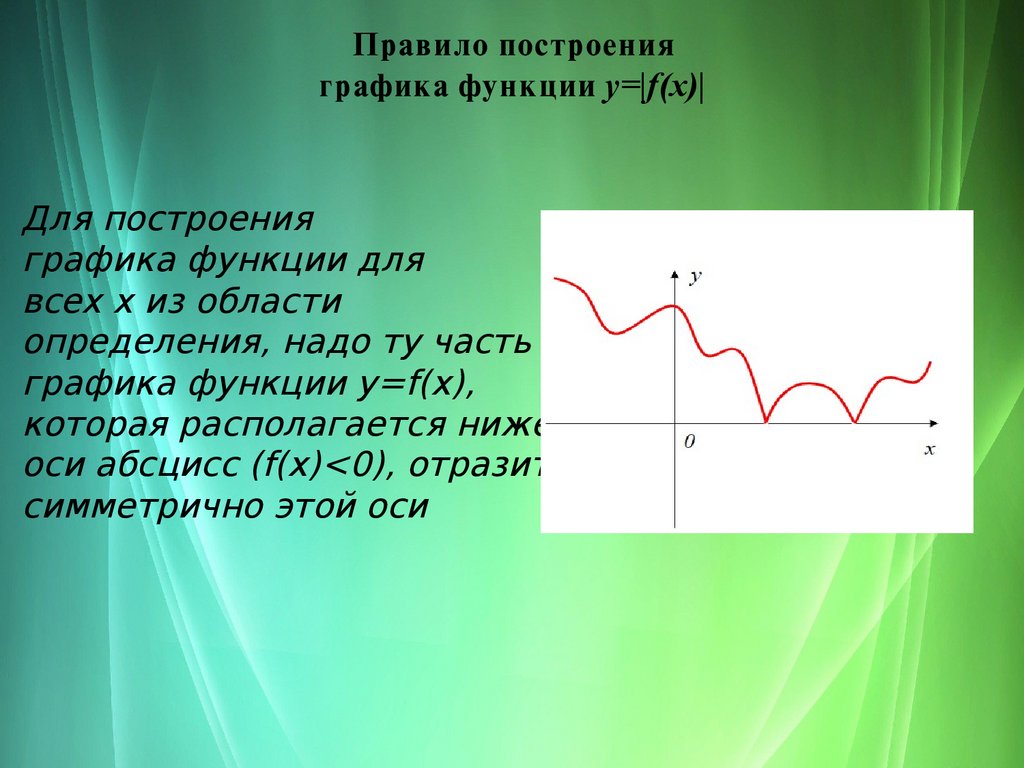
Правило построения
графика функции y=|f(x)|
Для построения
графика функции для
всех x из области
определения, надо ту часть
графика функции y=f(x),
которая располагается ниже
оси абсцисс (f(x)<0), отразить
симметрично этой оси

7.

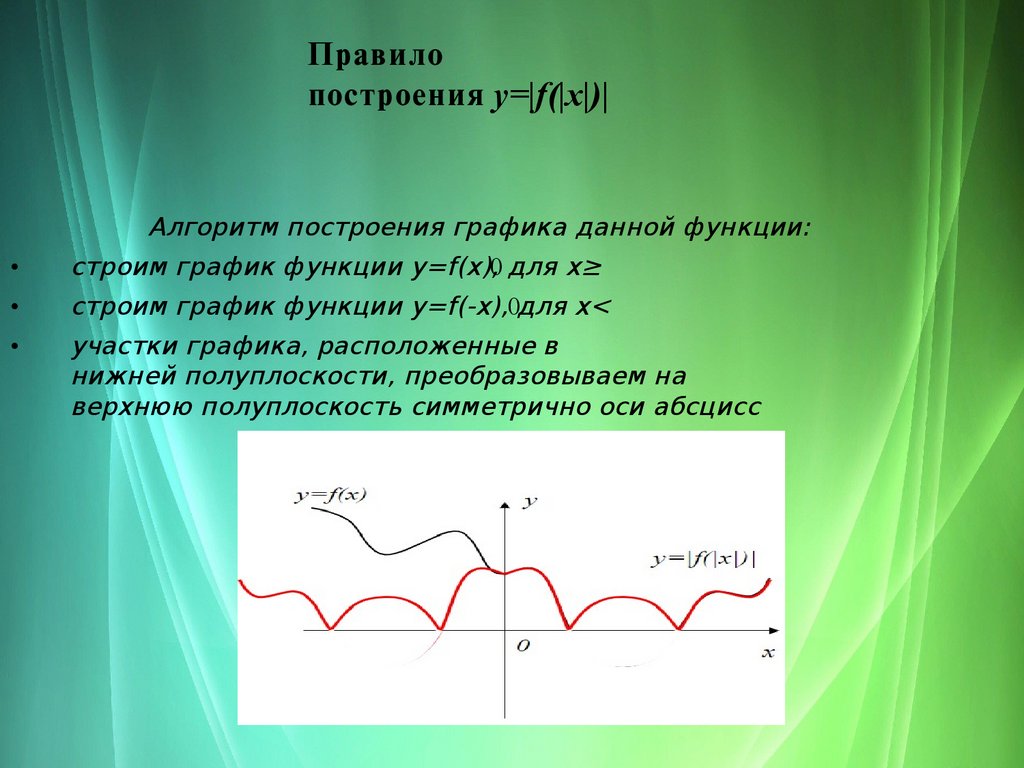
Правило
построения y=|f(|x|)|
Алгоритм построения графика данной функции:
строим график функции y=f(x),0 для x≥
строим график функции y=f(-x),0для x<
участки графика, расположенные в
нижней полуплоскости, преобразовываем на
верхнюю полуплоскость симметрично оси абсцисс

8.

Вывод
Для построения графика функции у = f |(х)|:
1.Построить график функции у = f(х) для х>0;
2.Построить для х<0 часть графика, симметричную
построенной относительно оси ОУ.
Для построения графика функции у = | f(х) |
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней
полуплоскости, т.е., где f(х) <0, строить кривые, симметричные
построенным графикам относительно оси абсцисс.
Для построения графика функции у = | f |(х)| |
1. Построить график функции у = f(х) для х>0.
2. Строим вторую часть графика, т. е. построенный график
симметрично отражаем относительно ОУ
3. Участки получившегося графика, расположенные в нижней
полуплоскости, преобразовываем на верхнюю полуплоскость
симметрично оси ОХ.