Сечение поверхности плоскостью

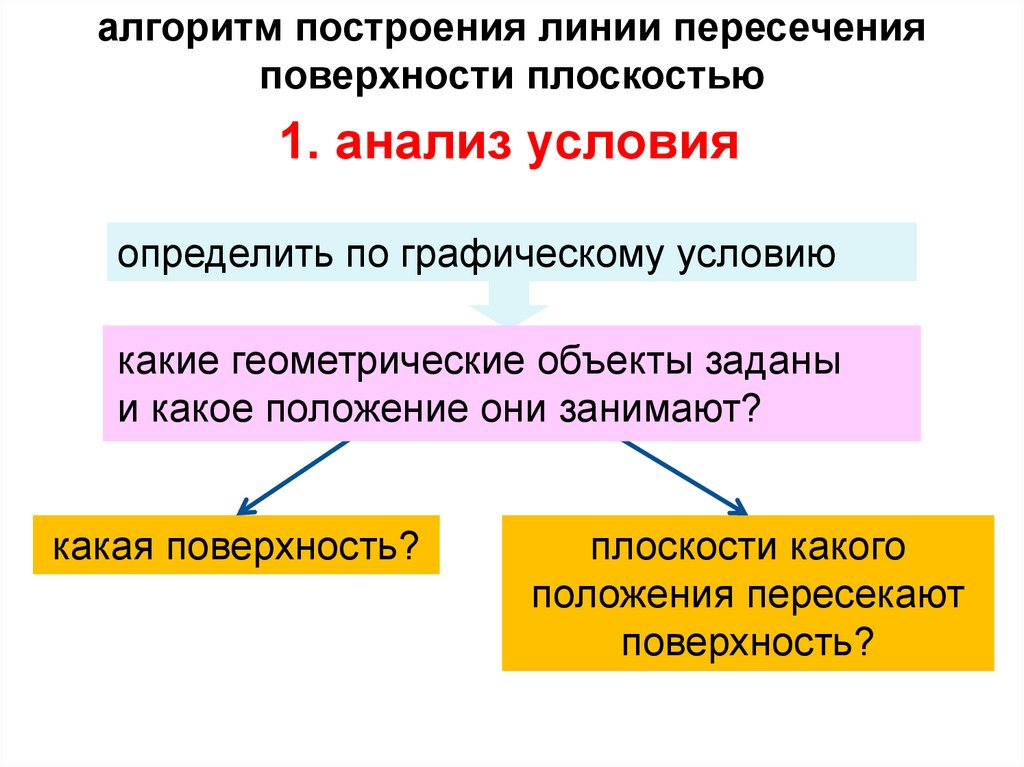
1.

2.

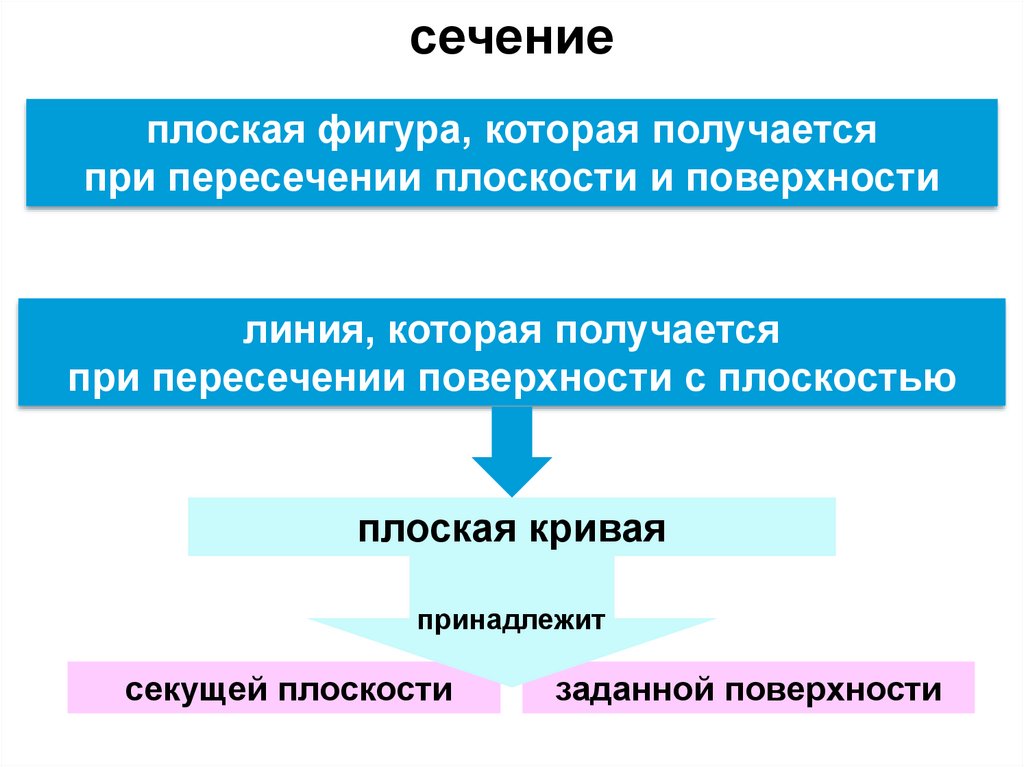
сечение
плоская фигура, которая получается
при пересечении плоскости и поверхности
линия, которая получается
при пересечении поверхности с плоскостью
плоская кривая
принадлежит
секущей плоскости
заданной поверхности

3.

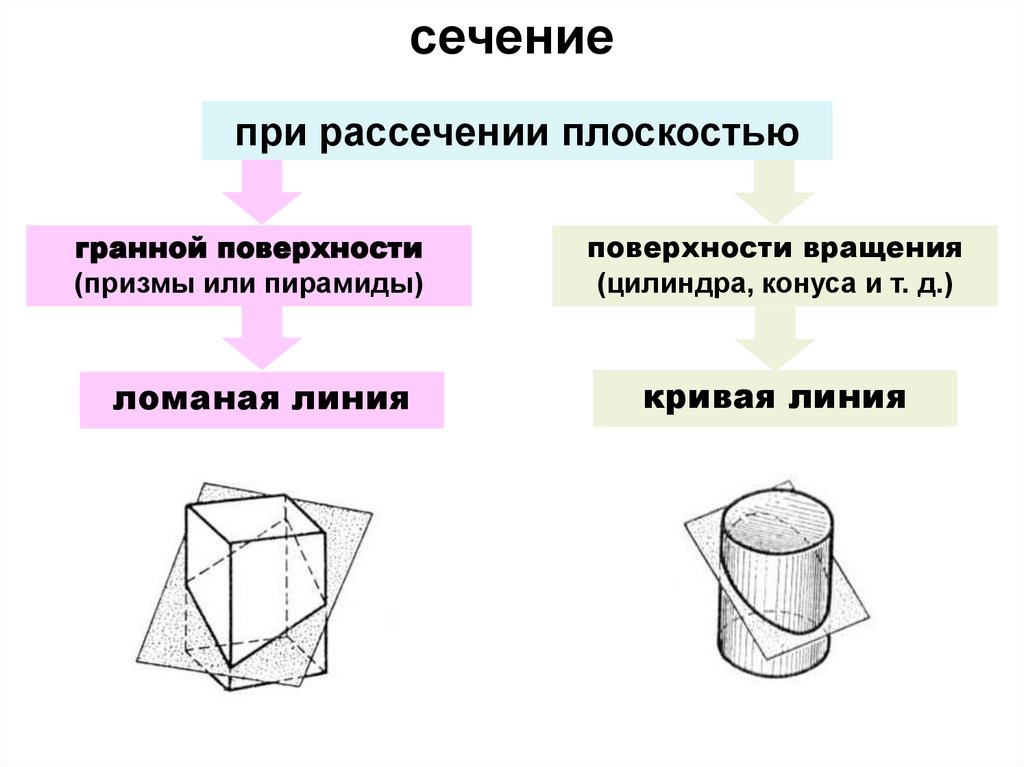
сечение
при рассечении плоскостью
гранной поверхности
(призмы или пирамиды)
ломаная линия
поверхности вращения
(цилиндра, конуса и т. д.)
кривая линия

4.

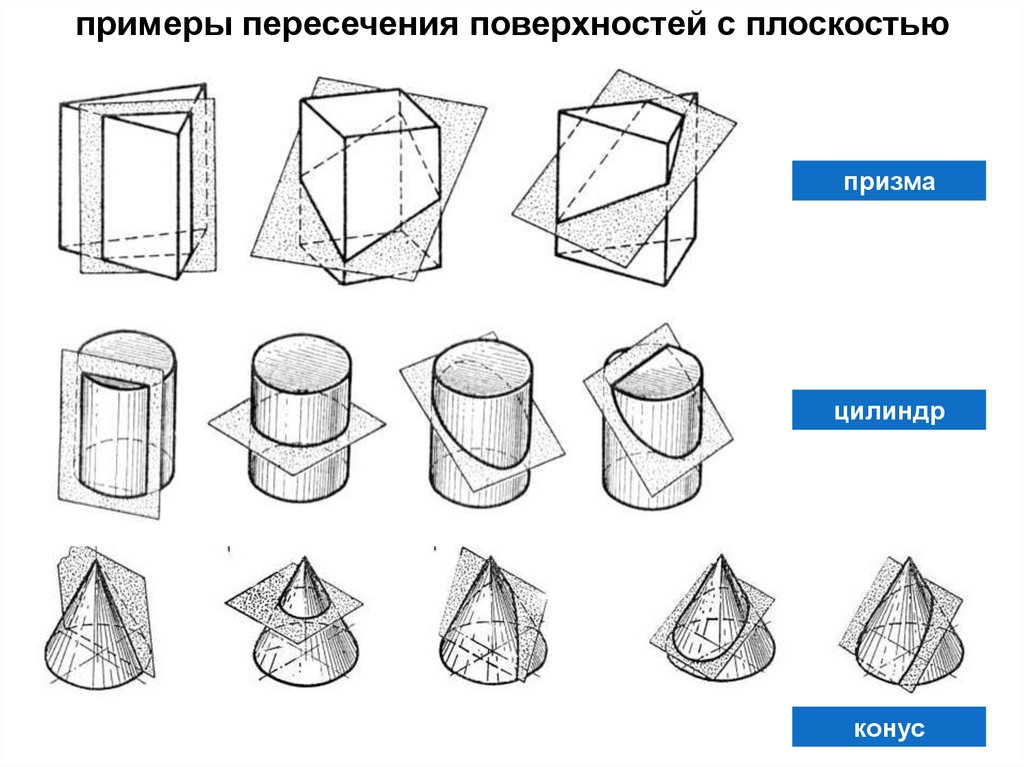
примеры пересечения поверхностей с плоскостью
призма
цилиндр
конус

5.

6.

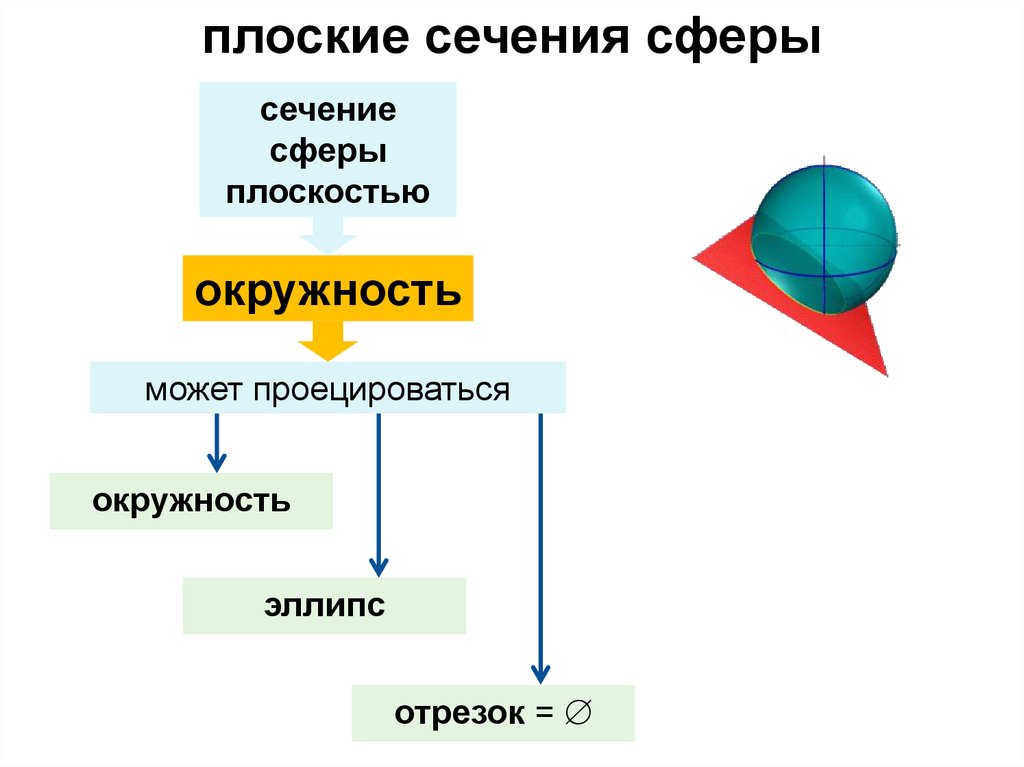
плоские сечения сферы
сечение
сферы
плоскостью
окружность
может проецироваться
окружность
эллипс
отрезок =

7.

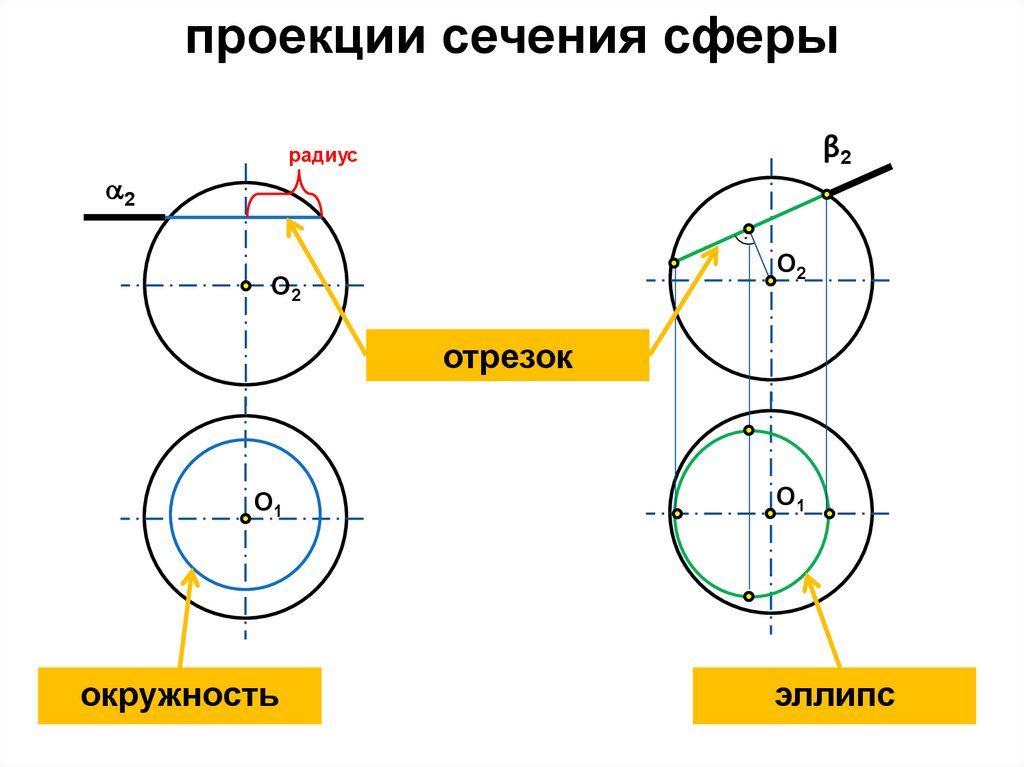
проекции сечения сферы
β2
радиус
2
О2
О2
отрезок
О1
окружность
О1
эллипс

8.

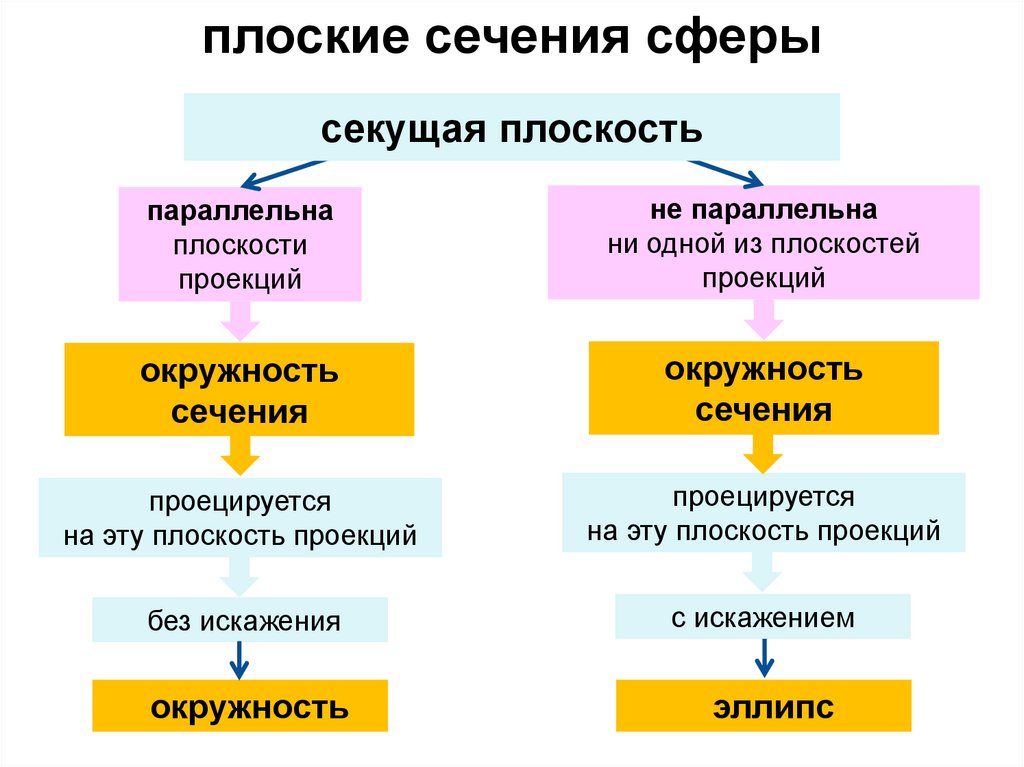
плоские сечения сферы
секущая плоскость
параллельна
плоскости
проекций
не параллельна
ни одной из плоскостей
проекций
окружность
сечения
окружность
сечения
проецируется
на эту плоскость проекций
проецируется
на эту плоскость проекций
без искажения
с искажением
окружность
эллипс

9.

10.

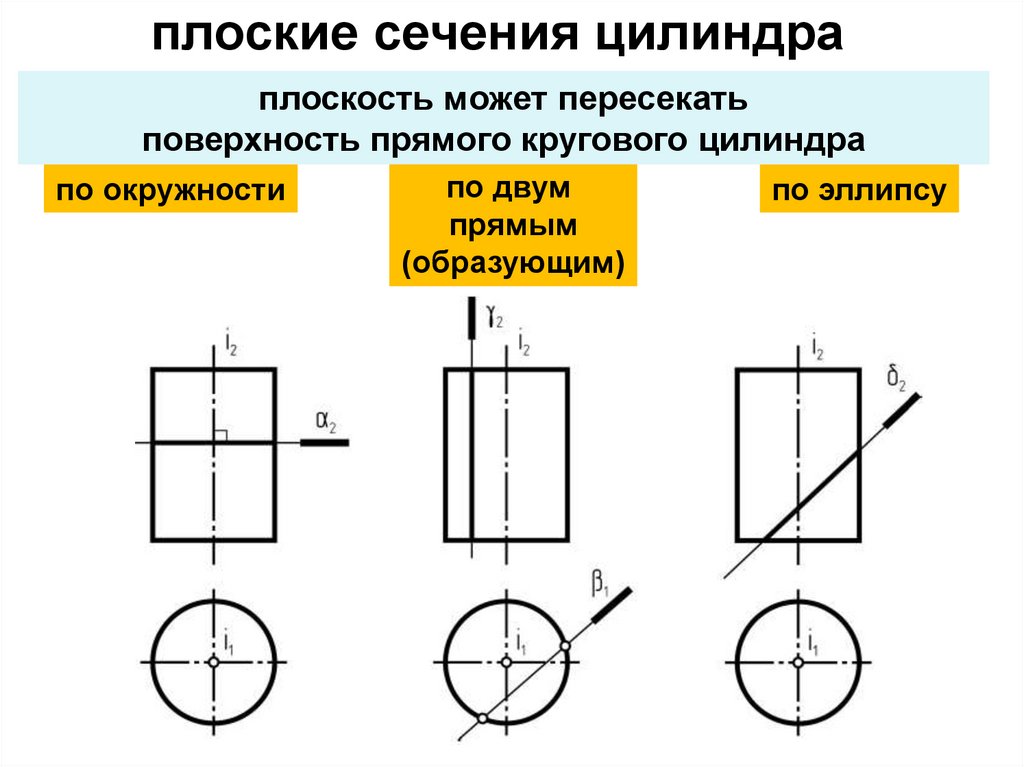
плоские сечения цилиндра
плоскость может пересекать
поверхность прямого кругового цилиндра
по окружности
по двум
прямым
(образующим)
по эллипсу

11.

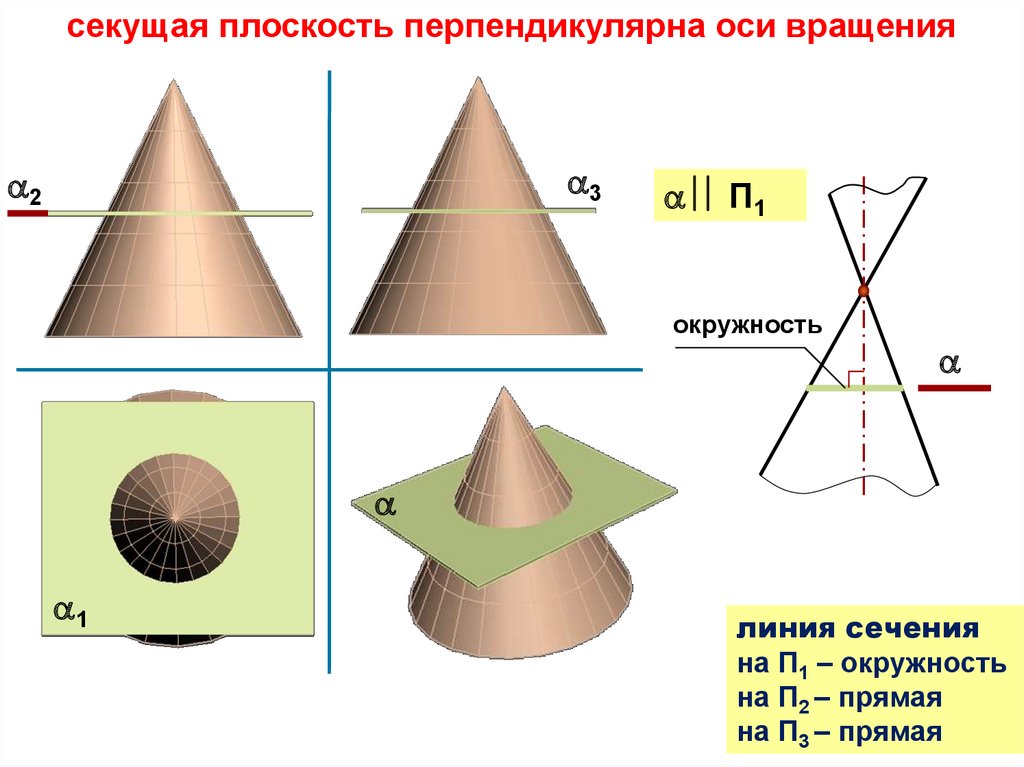
секущая плоскость перпендикулярна
оси вращения прямого кругового цилиндра
2
3
П1
П2
П3
окружность
1
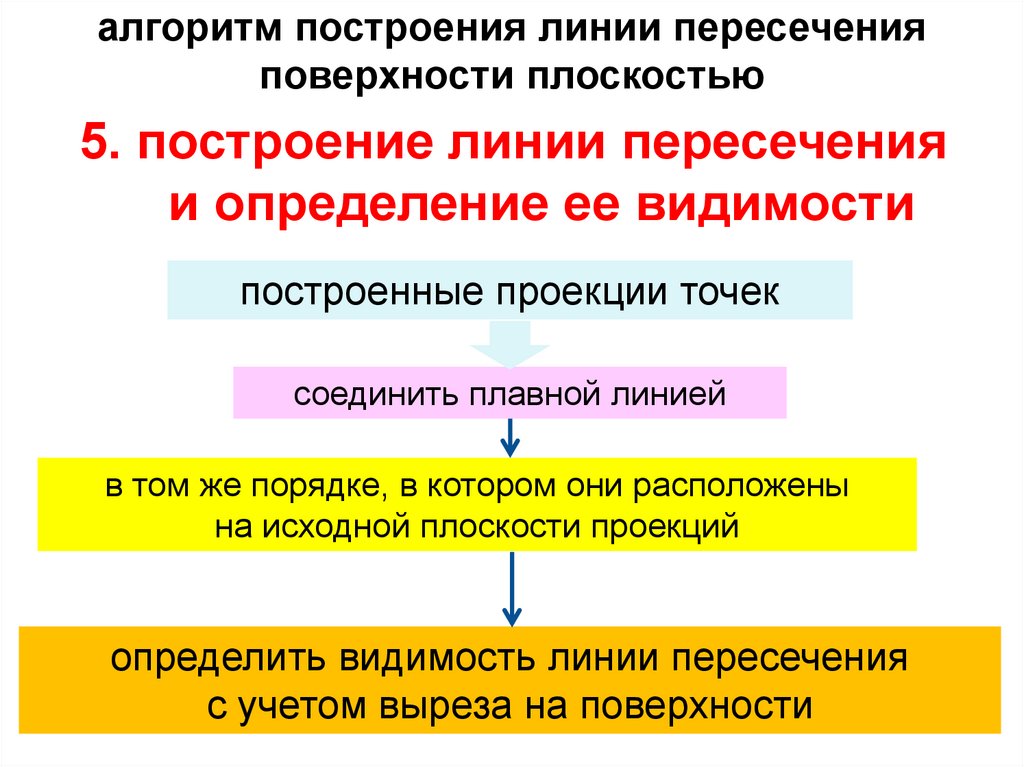
линия сечения
на П1 – окружность (очерк проецирующего цилиндра)
на П2 – прямая (вырожденная проекция плоскости)
на П3 – прямая (вырожденная проекция плоскости)

12.

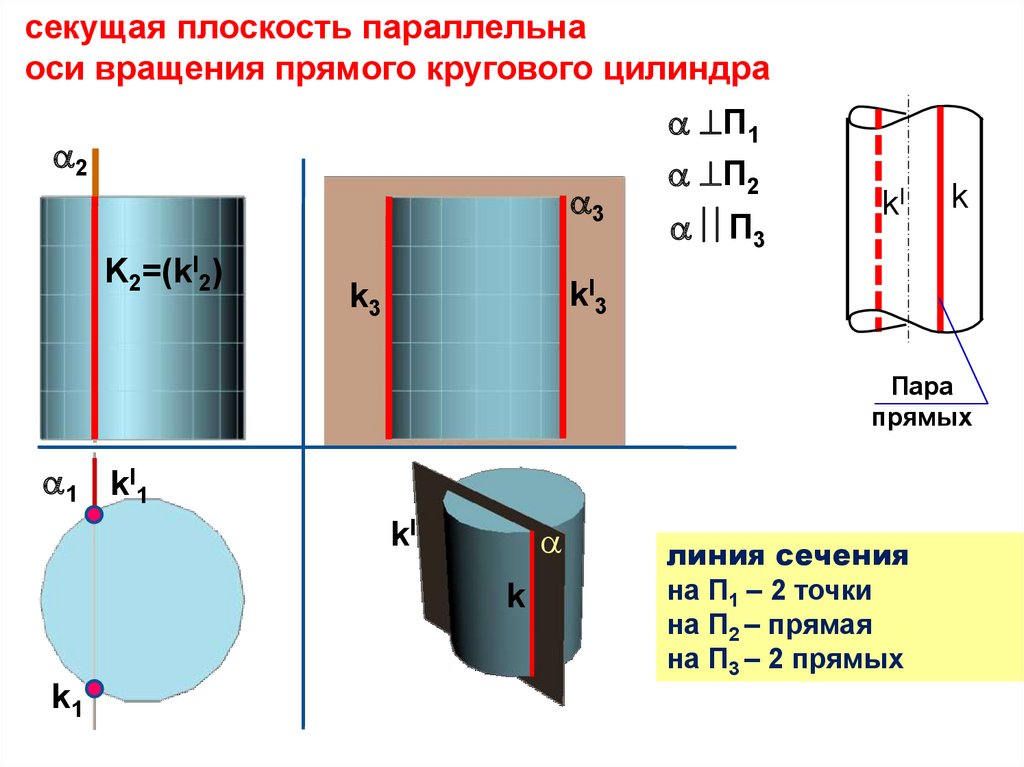
секущая плоскость параллельна
оси вращения прямого кругового цилиндра
2
3
K2=(kI2)
П1
П2
П3
kI
k
kI3
k3
Пара
прямых
1 kI1
kI
k
k1
линия сечения
на П1 – 2 точки
на П2 – прямая
на П3 – 2 прямых

13.

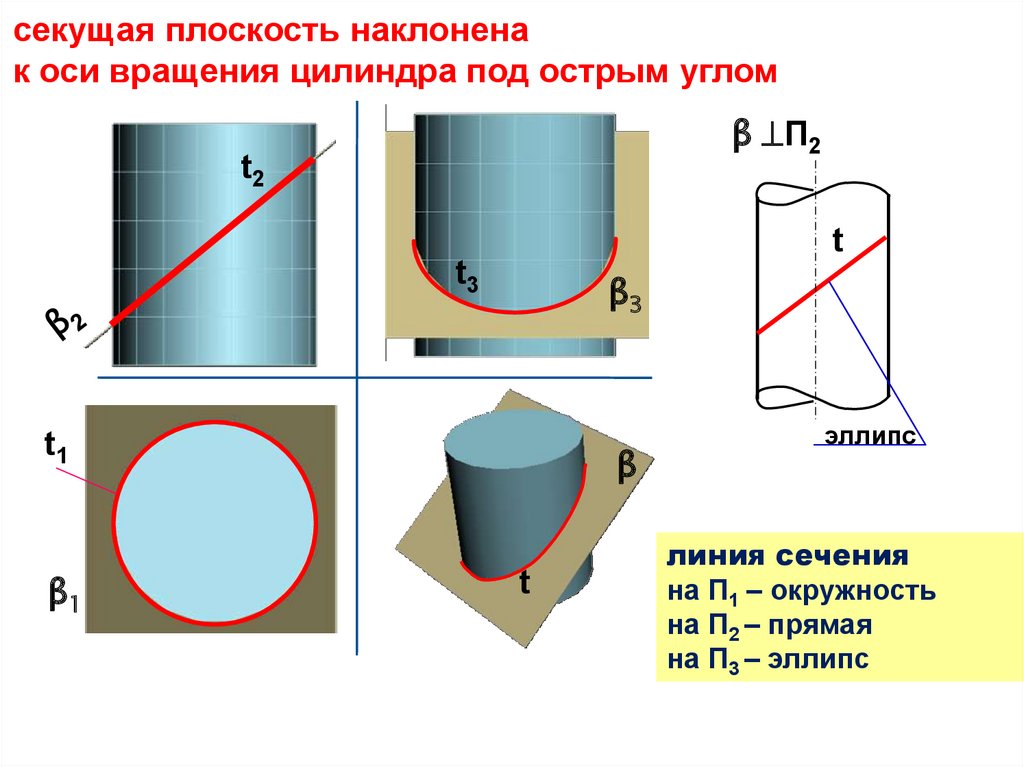
секущая плоскость наклонена
к оси вращения цилиндра под острым углом
β П2
t2
t
t3
β3
t1
β1
β
t
эллипс
линия сечения
на П1 – окружность
на П2 – прямая
на П3 – эллипс

14.

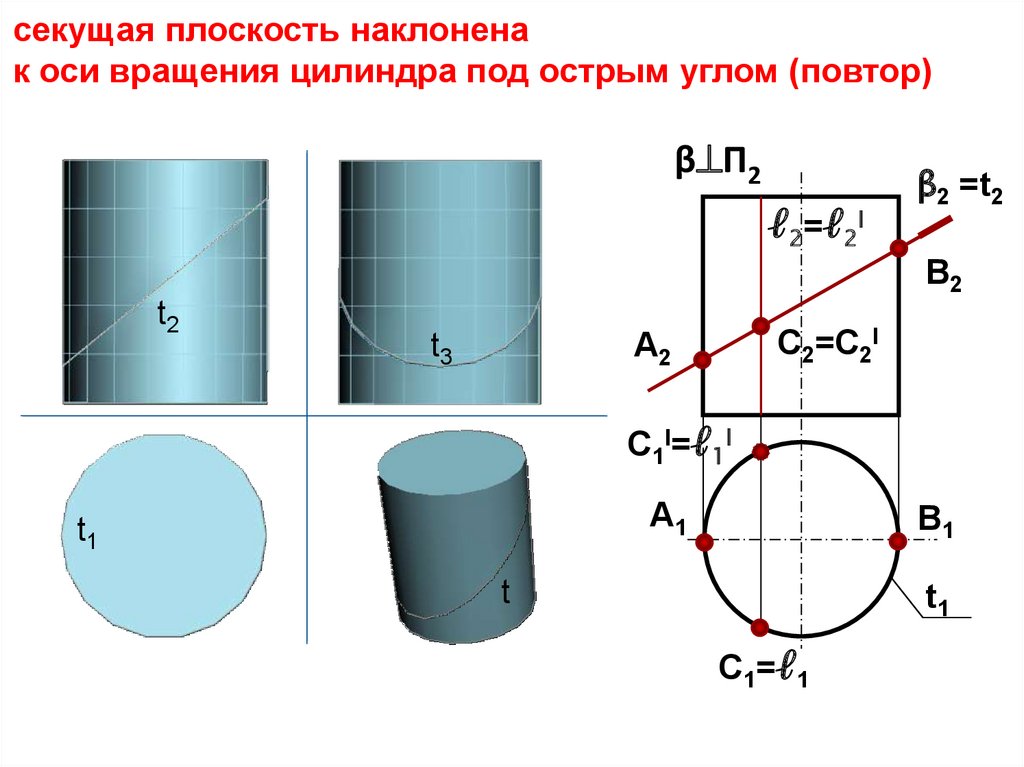
секущая плоскость наклонена
к оси вращения цилиндра под острым углом (повтор)
β П2
ℓ2=ℓ2I
β2 =t2
В2
t2
С2=С2I
А2
t3
С1I=ℓ1I
А1
t1
В1
t
t1
С1=ℓ1

15.

16.

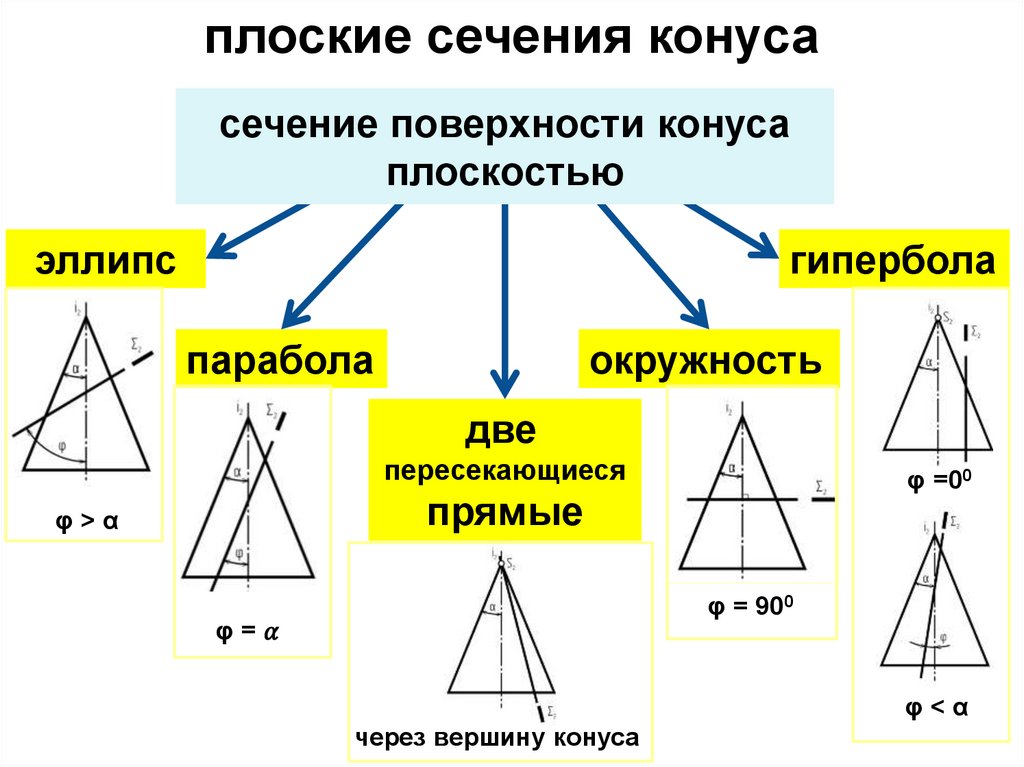
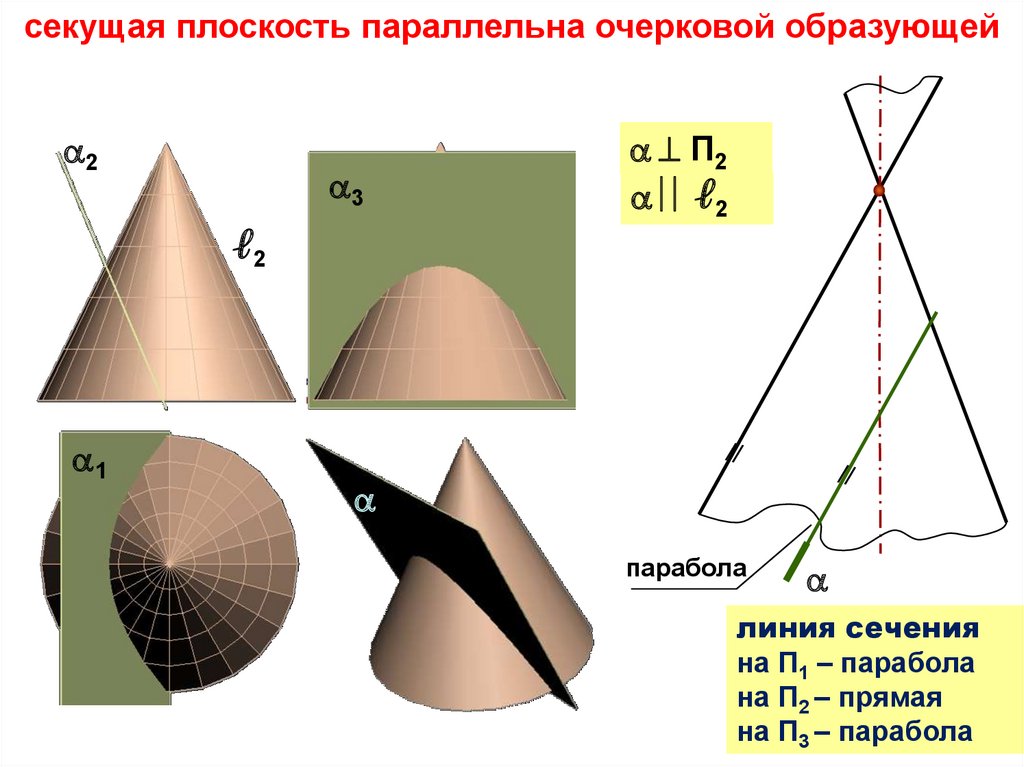
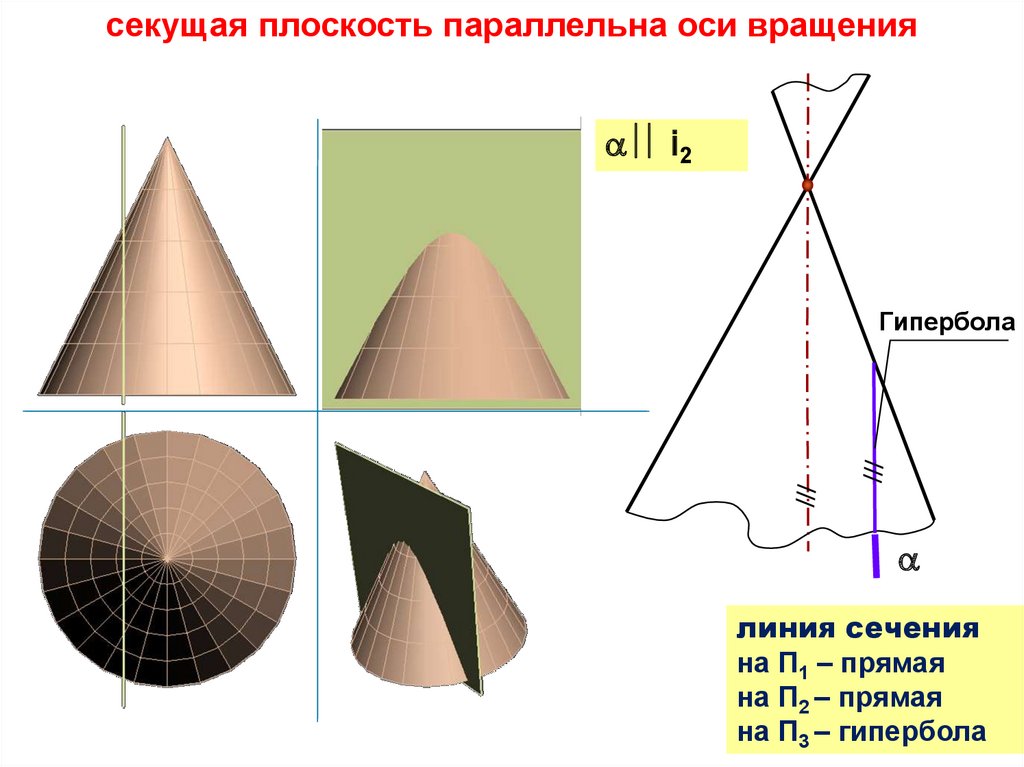
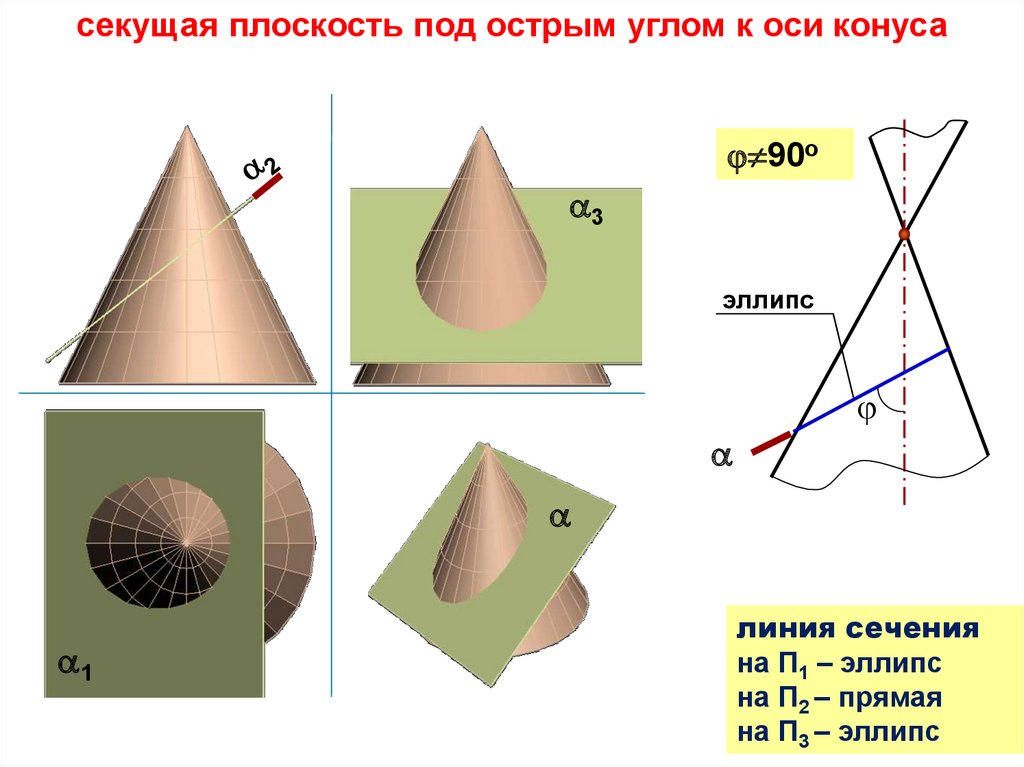
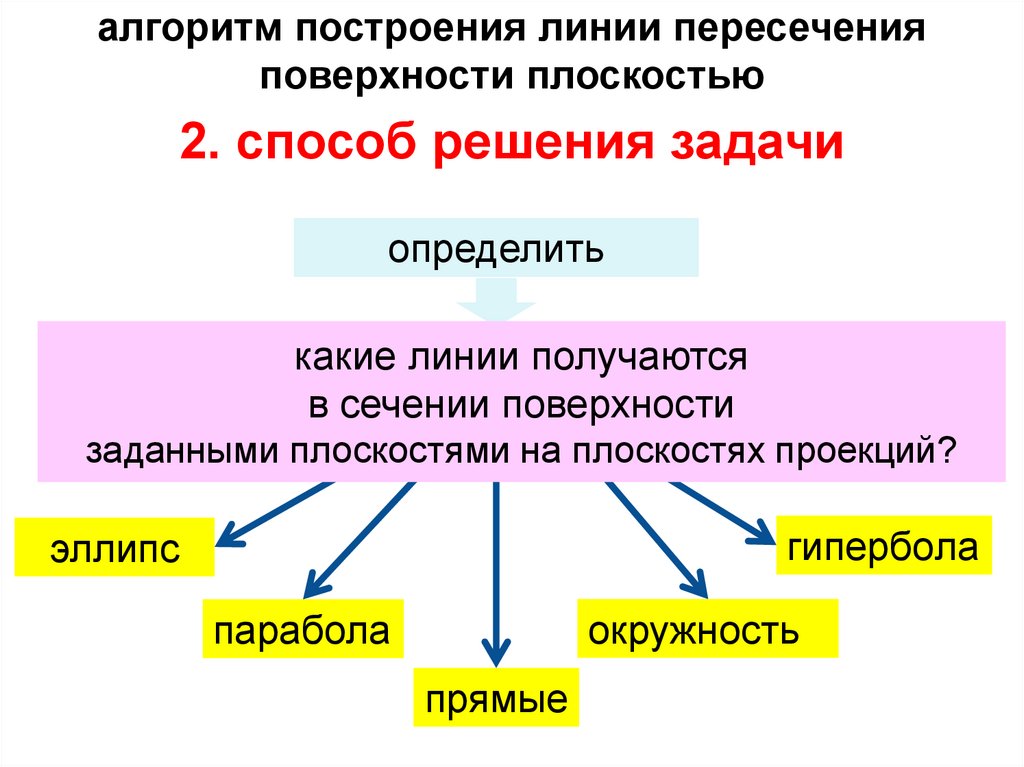
плоские сечения конуса
сечение поверхности конуса
плоскостью
эллипс
гипербола
парабола
окружность
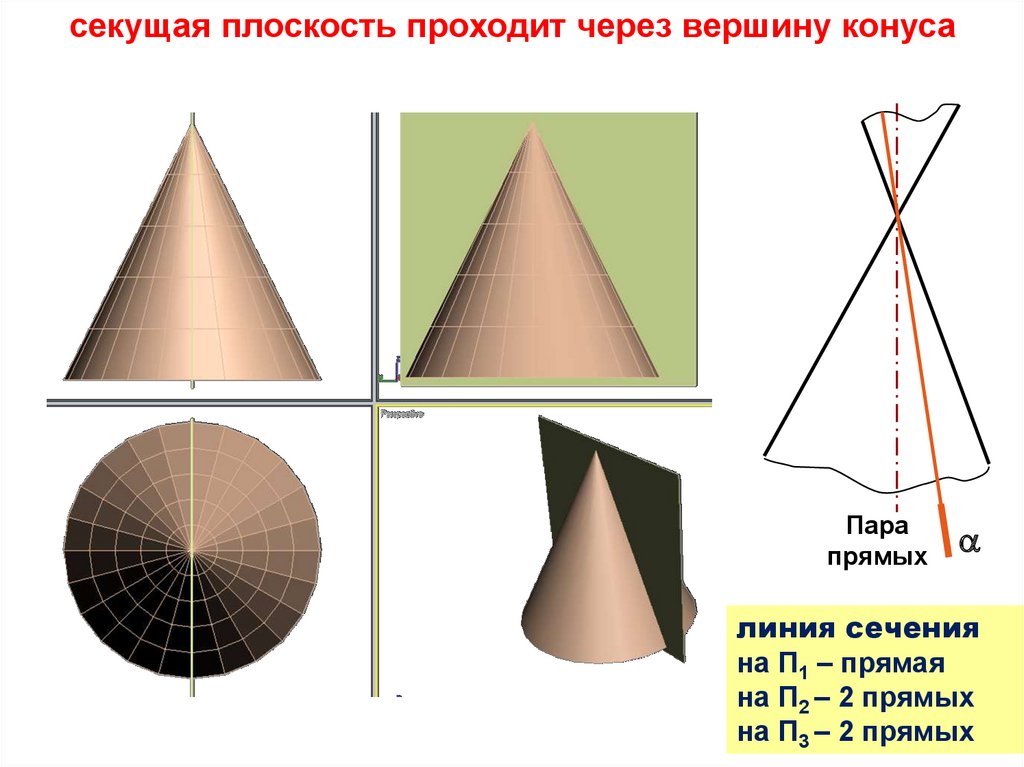
две
пересекающиеся
φ =00
прямые
φ>α
φ = 900
φ=