Похожие презентации:
Бинарные отношения
1. БИНАРНЫЕ ОТНОШЕНИЯ
Вводный курс математики2. БИНАРНЫЕ ОТНОШЕНИЯ
в Z:8>5 – истинно; 5>10 – ложно
На множестве точек плоскости:
Можно сказать, какая из точек плоскости
наиболее удалена от данной прямой
этой плоскости
Различные пары элементов некоторого
множества связаны отношением
(двуместным или бинарным)
3. БИНАРНЫЕ ОТНОШЕНИЯ
На множестве X определено бинарноеотношение, если задано подмножество
R декартова произведения X X
R X X
Бинарное отношение – соответствие из X в X
Если (x,y) R, то “x и y связаны отношением R”
xRy
R(x,y)
4. Способы задания бинарного отношения
1. Перечисление элементов:R={(1,1),(2,2),(6,6),(1,2),(1,6),(2,6)}
определено на множестве X={1,2,6}
2. Бинарное отношение - область истинности
некоторого двухместного предиката
R = IP - область истинности P(x,y): "x делит y"
3. Характеристическое свойство:
R = { (x,y) Z Z | x>3y }
5. Способы задания бинарного отношения
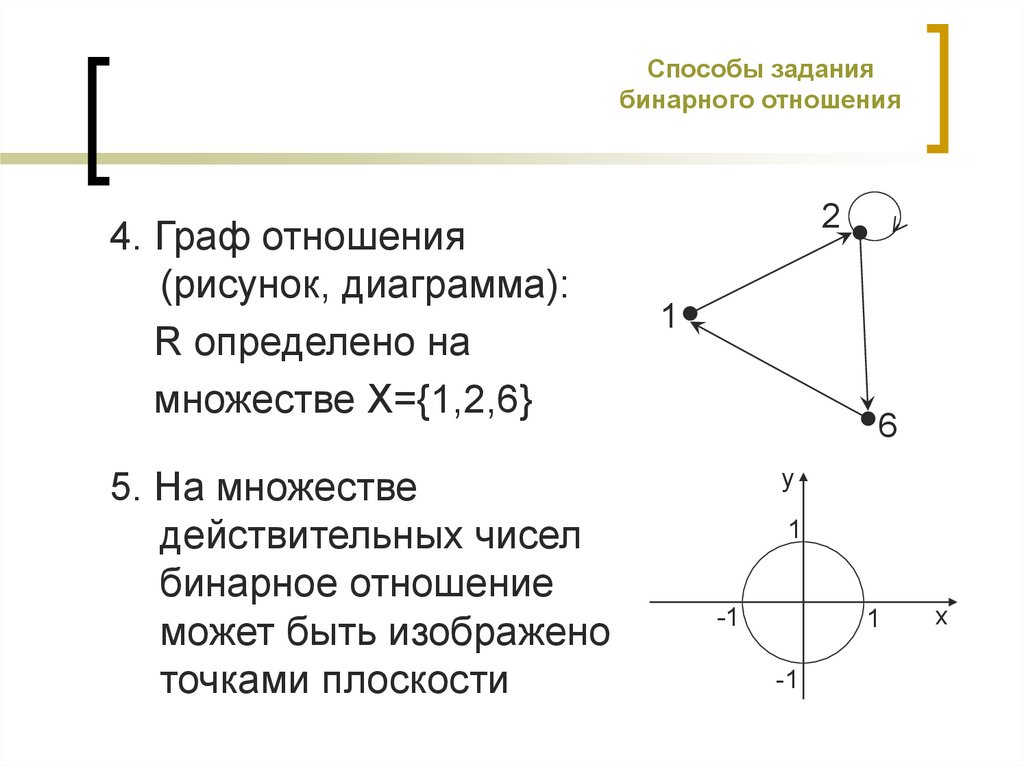
4. Граф отношения(рисунок, диаграмма):
R определено на
множестве X={1,2,6}
5. На множестве
действительных чисел
бинарное отношение
может быть изображено
точками плоскости
2
1
6
y
1
-1
1
-1
x
6. Способы задания бинарного отношения
6. Матричный способ:R
1
2
6
1
1
1
0
2
0
1
0
6
1
0
1
X={1,2,6}
Если (a,b) R, то на
пересечении строки
с номером a и столбца
с номером b ставится 1
7. Свойства бинарного отношения
R - бинарное отношение, определенное на множестве X1. R рефлексивно, если x X (x,x) R
R1 = { (x,y) Z Z | x y }
x Z x x
2. R симметрично, если
x,y X [ (x,y) R (y,x) R ]
R2 = { (x,y) Z Z | (x-y) кратно 2 }
x,y Z [ (x-y) кратно 2 (y-x) кратно 2 ]
8. Свойства бинарного отношения
R - бинарное отношение, определенное на множестве X3. R транзитивно, если
x,y,z X [ (x,y) R & (y,z) R (x,z) R ]
Для R1:
R1 = { (x,y) Z Z | x y }
x,y,z Z [ x y & y z x z ]
4. R антирефлексивно, если x X (x,x) R
R3 = { (x,y) Z Z | x>y }
x Z (x>x), т.е. x x
9. Свойства бинарного отношения
R - бинарное отношение, определенное на множестве X5. R антисимметрично, если
x,y X [ (x,y) R & (y,x) R x=y ]
R1 = { (x,y) Z Z | x y }
Для R1:
x,y Z [ x y & y x x=y ]
6. R линейно, если
x,y X [ (x,y) R V (y,x) R V x=y ]
Для R1:
x,y Z [ x y V y x V x=y ]
10. Отношение порядка
Отношение частичного порядка –рефлексивное, транзитивное и
антисимметричное бинарное отношение
R1 = { (x,y) Z Z | x y }
Отношение строгого порядка –
антирефлексивное, транзитивное,
антисимметричное и линейное
бинарное отношение
R3 = { (x,y) Z Z | x>y }
11. Частично упорядоченное множество
A< A, > – ЧУМ
Частично упорядоченное множество –
множество, на котором задано отношение
частичного порядка
1) < Z, > – ЧУМ
2) < P(A), > – ЧУМ
3) На N определим R: x R y x | y
Рефлексивность: x N (x | x)
Транзитивность: x,y,z N (x | y & y | z x | z)
Антисимметричность: x,y N (x | y & y | x x=y)
< N, R > - ЧУМ
< Z, R > - не является ЧУМ
12. Частично упорядоченное множество
Элемент a A частично упорядоченногомножества < A, > называется
наибольшим элементом, если x A x a
Наименьший элемент ???
Элемент a A частично упорядоченного
множества < A, > называется
максимальным элементом, если:
x A (если x сравним с a, то x a)
Минимальный элемент ???
13. Частично упорядоченное множество
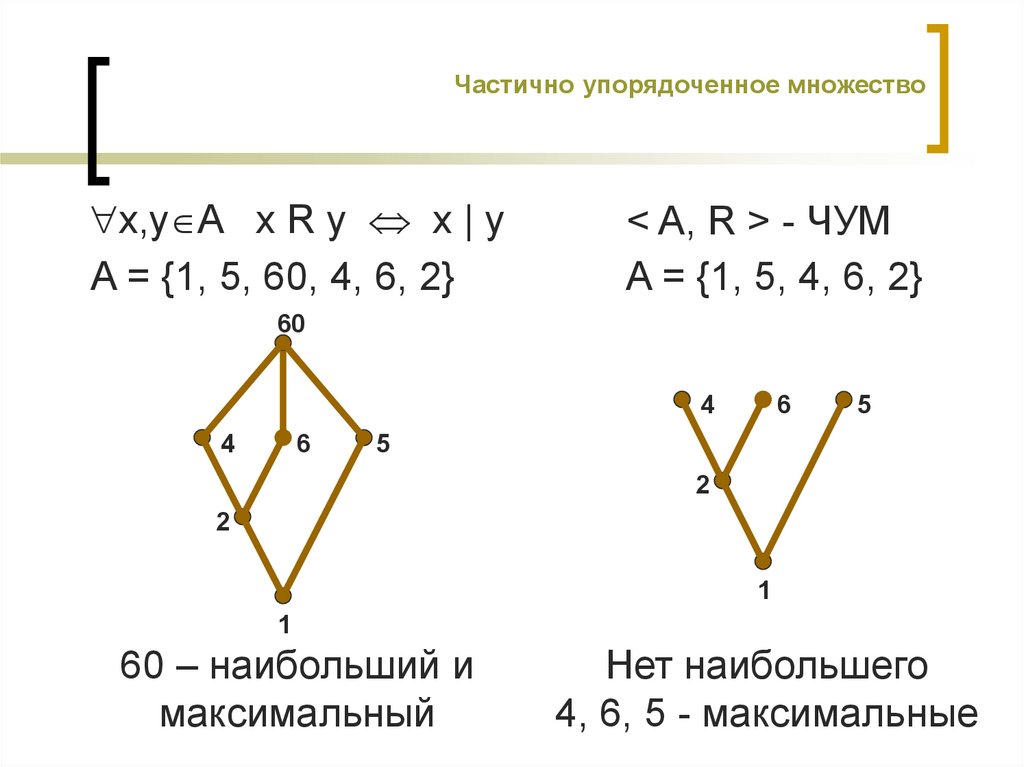
x,y A x R y x | yA = {1, 5, 60, 4, 6, 2}
< A, R > - ЧУМ
A = {1, 5, 4, 6, 2}
60
4
4
6
6
5
5
2
2
1
1
60 – наибольший и
максимальный
Нет наибольшего
4, 6, 5 - максимальные
14. Отношение эквивалентности
Отношение эквивалентности –рефлексивное, симметричное и
транзитивное бинарное отношение
R3 = { (x,y) Z Z | x>y } - не рефлексивно
R1 = { (x,y) Z Z | x y } - не симметрично
R2 = { (x,y) Z Z | (x-y) кратно 2 }
Рефлексивность: x Z ( (x-x) кратно 2 )
Симметричность – проверена (см. ранее)
Транзитивность:
x,y,z Z [ ((x-y) кратно 2) & ((y-z) кратно 2)
((x-y)+(y-z)) кратно 2 (x-z) кратно 2 ]
R3 - отношение эквивалентности
15. УПРАЖНЕНИЕ
Докажите:m Z m>1
R = { (x,y) Z Z | (x-y) кратно m } –
отношение эквивалентности
16. Классы эквивалентности
Семейство { Xk | k K, Xk X } образуетразбиение множества X на классы Xk,
если:
1) k K Xk
2) m,k K [ m k Xm Xk = ]
3) X = U Xk
k K
A = {1,2,3,4,5} можно разбить на классы:
A1 = {3}, A2 = {1,4}, A3 = {2,5}
17. Классы эквивалентности
Всякому разбиению множества X на классыXk отвечает бинарное отношение R,
задаваемое следующим образом:
(x,y) R т.т.т., когда k K (x Xk & y Xk)
Упражнение: Покажите, что R – отношение
эквивалентности
Любые два элемента одного класса
эквивалентны между собой
Никакие два элемента разных классов
не эквивалентны между собой
18. Классы эквивалентности
Пусть ~ – отношение эквивалентности,заданное на X, и a X
Класс Ka эквивалентности ~
c порождающим элементом a:
Ka = { x X | x ~ a }
{ (x,y) Z Z | (x-y) кратно 2 } -
отношение эквивалентности ~
K0 = { x Z | x ~ 0 } = { x Z | (x-0) кратно 2 } = 2Z
K1 = { x Z | x ~ 1 } = { x Z | (x-1) кратно 2 } = 2Z+1
19. Свойства классов эквивалентности
Пусть ~ – отношение эквивалентности, заданное на X1) Любой класс Ka не пуст
a ~ a (рефлексивность), т.е. a Ka
2) Если x Ka и y Ka, то x ~ y
x Ka и y Ka, т.е. x ~ a и y ~ a
По симметричности: y ~ a a ~ y
По транзитивности: x ~ a & a ~ y x ~ y
3) Если a ~ b, то Ka = Kb
Пусть x Ka, тогда x ~ a транзитивность
x ~ b x Kb
Но по условию a ~ b
Аналогично: Kb Ka
Ka Kb
Итак, Ka = Kb
20. Свойства классов эквивалентности
Пусть ~ – отношение эквивалентности, заданное на X4) Элементы из разных классов не
эквивалентны друг другу
Пусть Ka Kb
Пусть x Ka x ~ a Kx = Ka
Ka = Kb
Пусть y Kb y ~ b Ky = Kb
ПРОТИВОРЕЧИЕ
Если x ~ y, то Kx = Ky
5) Различные классы не пересекаются
Пусть Ka Kb. Пусть Ka Kb , т.е. x Ka Kb.
, Тогда x Ka и x Kb Kx = Ka и Kx = Kb
ПРОТИВОРЕЧИЕ
Ka = Kb
21. ТЕОРЕМА
Всякое отношение эквивалентности, заданноена множестве X, определяет разбиение
множества X на классы эквивалентности
Доказательство: Пусть ~ – отношение
эквивалентности на X
{ Xk | k K, Xk X } – множество классов
эквивалентности по отношению ~
1) По свойству 1: k K
Xk
2) По свойству 5: m,k K [ m k Xm Xk = ]
22. Доказательство ТЕОРЕМЫ
продолжение3) k K Xk X, т.е. U Xk X
k K
a X k K (a Xk) a U Xk X U Xk
k K
k K
Итак, X = U Xk
k K
Следовательно, { Xk | k K, Xk X } образует
разбиение множества X на классы Xk
Теорема доказана
23. Фактор-множество
Фактор-множеством множества X поотношению эквивалентности R называется
множество, каждый элемент которого
является одним из классов эквивалентности
Обозначение:
X/R
Пример 1: R = { (x,y) | (x-y) кратно 2 } на Z
K0 = 2Z
K1 = 2Z+1
X / R = { 2Z, 2Z+1 }
24. Фактор-множество
Пример 2: X = { (p,q) | p,q Z, q 0 }На X определим отношение
эквивалентности R:
(p,q) R (m,n) т.т.т. p n q m = 0
p m
p n q m
Это равенство дробей:
q n
Рациональное число – класс эквивалентности
(все равные дроби с точностью до
сократимости)
X / R можно рассматривать как множество
рациональных чисел






















 Математика
Математика








