Отношения. Бинарные отношения и их свойства

1. Дискретная математика

Отношения.
Бинарные отношения
и их свойства

2.

• Определение.
Отношение
есть
взаимная формальная связь различных
величин, предметов, действий, то есть
элементов некоторого множества.
Отношения в некоторых числовых
множествах могут выражаться терминами:
«быть равным», «быть больше», «быть не
меньше», «быть делителем» и т.д.
Отношения во множестве линий на
плоскости могут выражаться терминами: «быть
параллельными», «пересекаться», «касаться»
и т.д.

3.

• Декартовым (прямым) произведением множеств А×В
называется множество всех упорядоченных пар (всех
кортежей), в которых первый элемент принадлежит
множеству А, а второй элемент принадлежит множеству В.

4. Определение

Пусть задано множество М.
Рассмотрим декартово произведение
этого множества на себя М х М.

5. Определение

Пусть задано множество М.
Рассмотрим декартово произведение
этого множества на себя М х М.
• Подмножество R множества М х М
называется бинарным отношением R
на множестве М. Если пара (х;у)
принадлежит множеству R, говорят,
что элемент х находится в
отношении R с элементом у, и
записывают xRy.

6.

Подмножество R M n называется n-местным
отношением R на непустом множестве М. При
n=2 отношение R называется бинарным.
То есть бинарным отношением между
элементами множеств А и В называют любое
подмножество R множества АхВ и записывают
R АхВ.
Для отношения R обратным является
отношение R-1 BxA.

7.

Бинарные отношения принято записывать в
виде aRb, где а, b М. Запись читается как «а
и b находятся в отношении R».
Например, а||b (параллельные прямые), а b
(действительные числа), а = logc b и т.д.
Рассмотрим примеры бинарных отношений.
Бинарное отношение R: х у
показано на рис. Заштриховано
множество точек, для координат
которых это отношение
выполняется (истинно).

8.

Графики прямых и обратных бинарных
отношений, определенных на множестве
действительных чисел, симметричны
относительно биссектрисы I и III квадрантов.
Это свойство обратных бинарных отношений
используют при построении графиков
обратных функций, например: у = log2x и у=2х
Пример 1.
у = х2 и
у = x,
где х О
(рис. a);

9.

Способы задания бинарных отношений.
1. Перечислением элементов
V={a, b, c, d, e}, Т V2
T (a , b), (a , c), (a , d ), (b, c), ( b, d ), ( b, e), (c, a ),
(c, b), (c, d), (c, e), (d, b), (d, c), (e, c), (d, e)}
2.
Характеристическим свойством
2
A={1, 2, 3, 4, 5}, R Z
R={(x,y) x<y}
R={(1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4),
(3,5), (4,5) }
9

10.

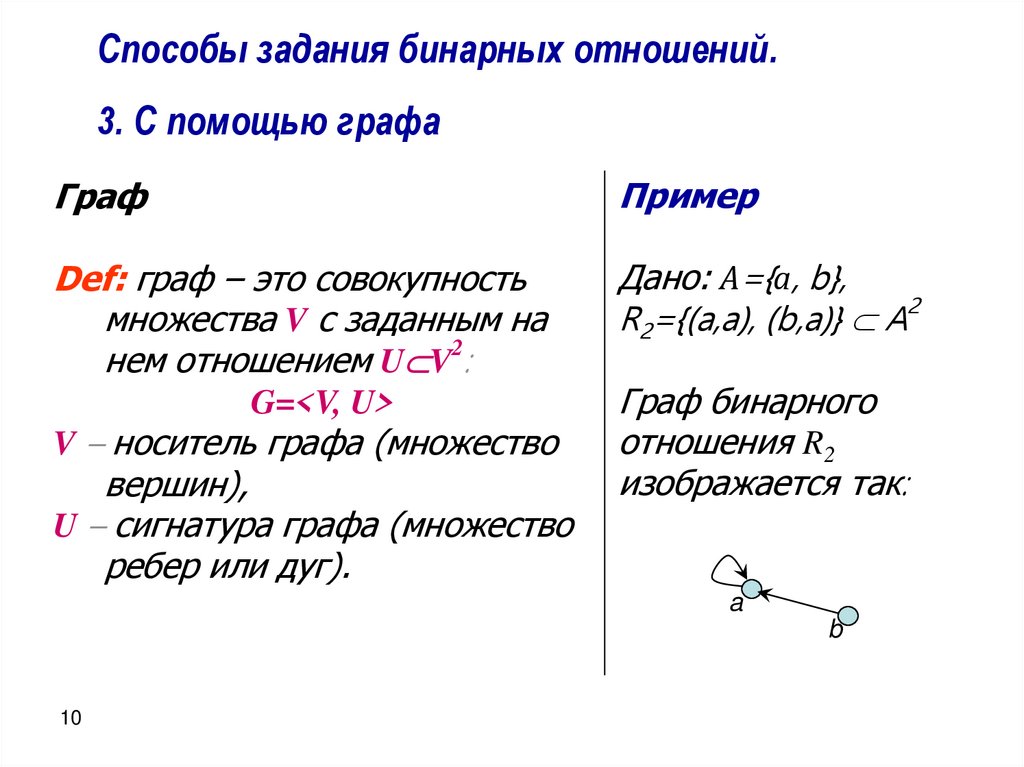
Способы задания бинарных отношений.
3. С помощью графа
Граф
Пример
Def: граф – это совокупность
множества V с заданным на
нем отношением U V2:
Дано: А={а, b},
R2={(a,a), (b,a)} A2
G=<V, U>
V – носитель графа (множество
вершин),
U – сигнатура графа (множество
ребер или дуг).
Граф бинарного
отношения R2
изображается так:
a
b
10

11.

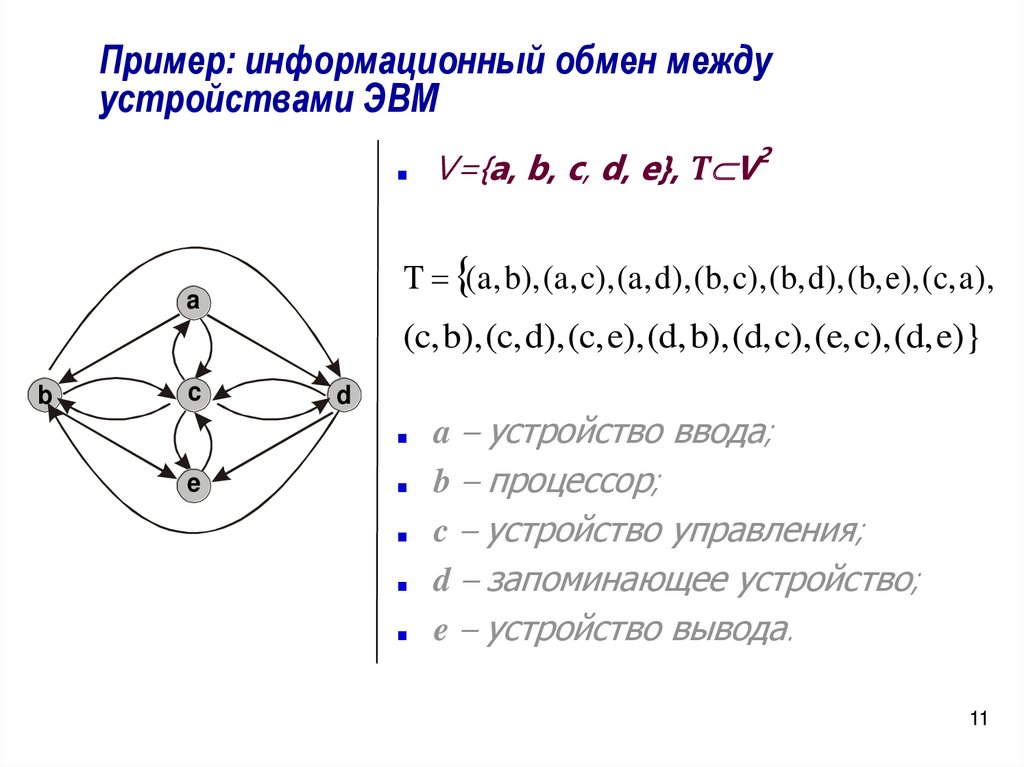
Пример: информационный обмен между
устройствами ЭВМ
V={a, b, c, d, e}, Т V2
T (a , b), (a , c), (a , d), (b, c), (b, d), (b, e), (c, a ),
a
(c, b), (c, d), (c, e), (d, b), (d, c), (e, c), (d, e)}
b
c
e
d
a – устройство ввода;
b – процессор;
c – устройство управления;
d – запоминающее устройство;
e – устройство вывода.
11

12.

• 4. С помощью графика
Бинарное отношение R: х у
показано на рис. Заштриховано
множество точек, для координат
которых это отношение
выполняется (истинно).

13.

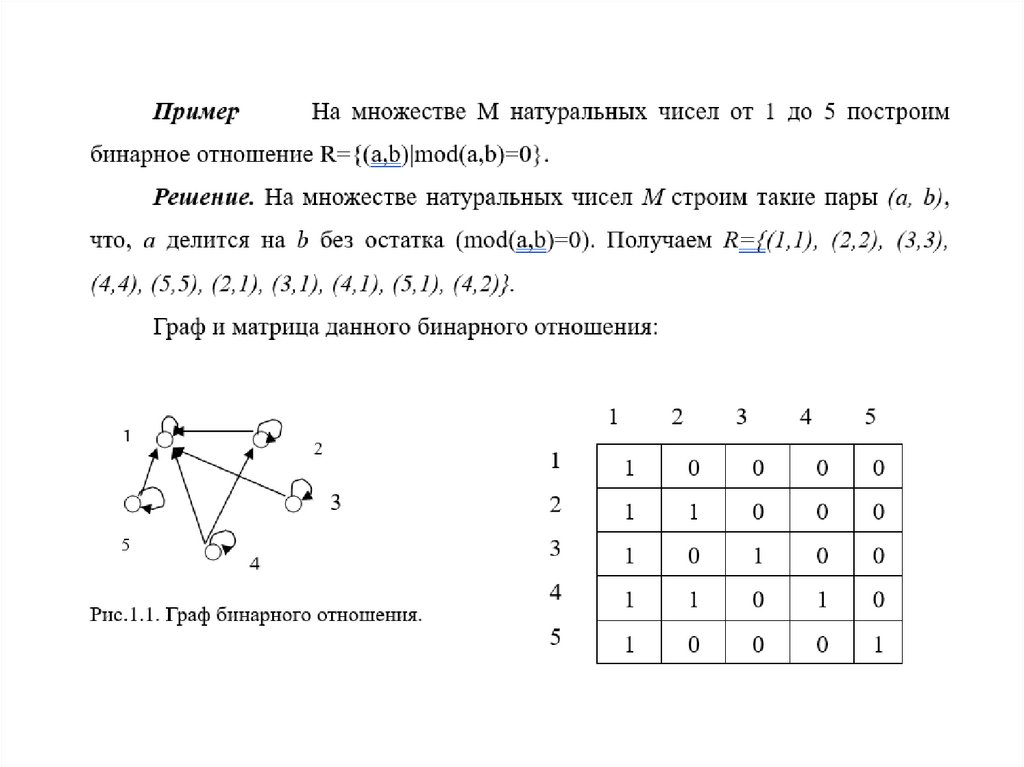
Способы задания бинарных отношений.
5. Матрица смежности
Пример
Def: матрица смежности
Дано: А={а, b},
бинарного отношения на
R2={(a,a), (b,a)} A2
множестве А={а1, а2, а3, …, an} –
это таблица размера n n,
Матрица смежности
в которой элемент cij ,
бинарного отношения
определяется следующим образом:
R представляется так:
2
1, если a i Ra j ;
cij
0 в противном случае
13
a b
a 1 0
b 1 0

14.

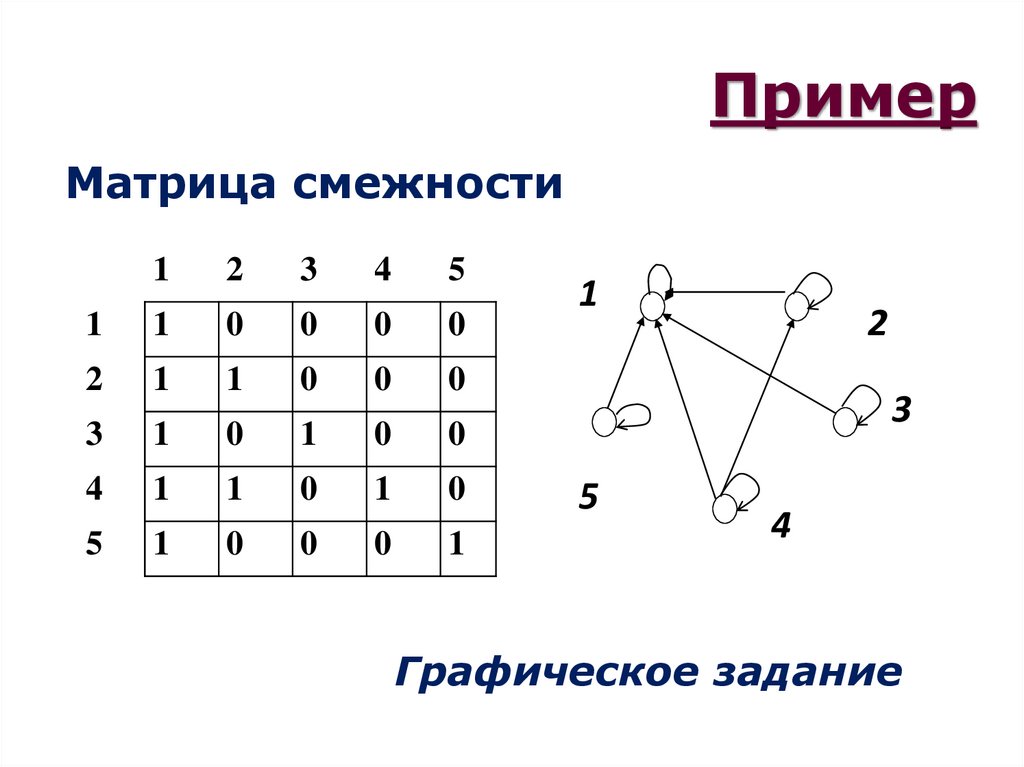
15. Пример

Матрица смежности
1
2
3
4
5
1
1
0
0
0
0
2
1
1
0
0
0
3
1
0
1
0
0
4
1
1
0
1
0
5
1
0
0
0
1
1
2
3
5
4
Графическое задание

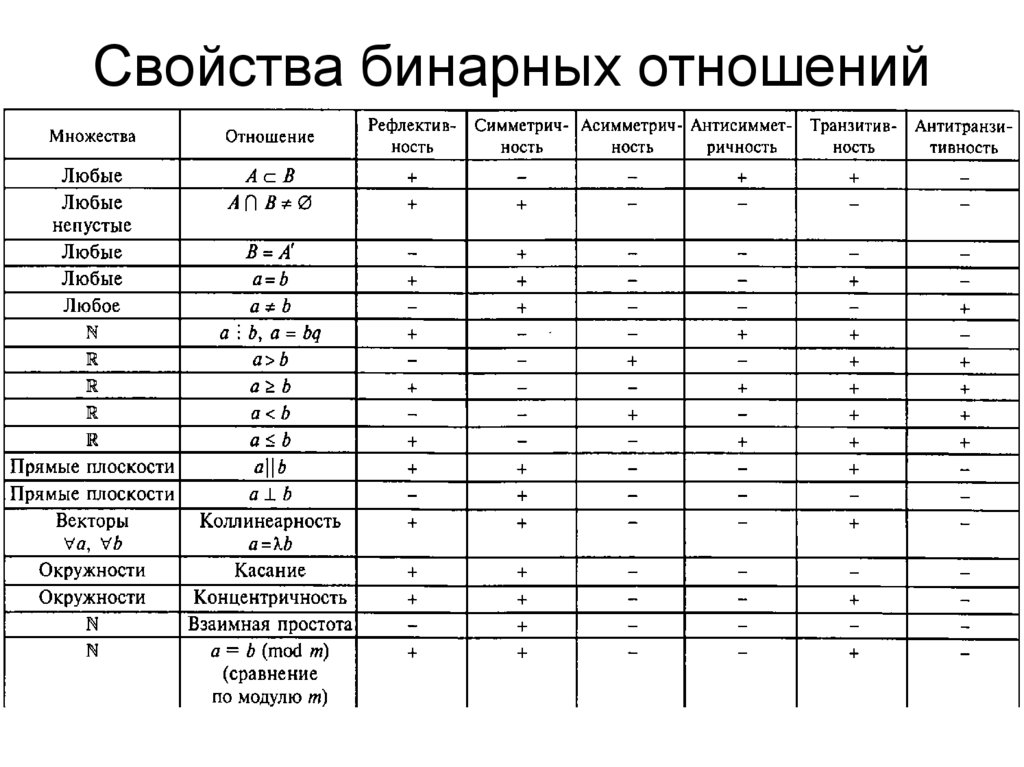
16. Свойства бинарных отношений:

1) рефлексивность:
a M a, a R
Например: «быть не больше»; «быть
делителем» на множестве N; «быть
коллинеарным» на множестве векторов;

17. Свойства бинарных отношений:

2) антирефлексивность:
a M a, a R
Это отношение имеет место, когда оно не
обладает свойством 1 для любых а,
например: «быть больше», «быть
младше», «быть перпендикулярной» на
множестве прямых и др.

18. Свойства бинарных отношений:

3) симметричность:
a, b M a, b R b, a R
Отношение R на множестве М называется
симметричным, если для любых a, b M
одновременно справедливо aRb и bRa
(т.е.R=R-1).
Например:
Симметрична параллельность прямых, так как
если а || b, то b || а. Симметрично отношение
«быть равным» на любом множестве или «быть
взаимно-простым» на N.

19. Свойства бинарных отношений:

4) антисимметричность:
a, b M a, b R, b, a R a b
Если для несовпадающих элементов а b
верно отношение aRb, то ложно bRa.
Антисимметричными являются отношения
«быть больше», «не меньше» на множестве R,
«быть делителем» на множестве N и др.

20. Свойства бинарных отношений:

5) транзитивность:
a, b, c M a, b R, b, c R a, c R
Если aRb и bRc, то aRс для любых a, b, c M.
Транзитивны отношения «быть больше», «быть
параллельным», «быть равным» и др.

21. Свойства бинарных отношений:

6) антитранзитивность:
a, b, c M a, b R, b, c R a, c R
Имеет место, когда отношение не обладает
свойством 5. Например, «быть
перпендикулярным» на множестве прямых
плоскости ( а b, b с, но неверно a с).

22. Свойства бинарных отношений:

7) асимметричность:
a, b M a, b R b, a R
Ни для одной пары а и b не выполняется
одновременно aRb и bRa.
Например: «быть больше»; «быть меньше»;
«быть отцом».

23. Свойства бинарных отношений:

8) связность:
a, b M a, b R или b, a R
Для любых а и b, если а b, то aRb или bRa.
Например: «быть больше», «быть меньше» на
множестве N, R; «быть больше или равным»,
«быть меньше или равным» на множестве
обыкновенных дробей.
Каждое конкретное отношение может обладать
или не обладать указанным свойством.

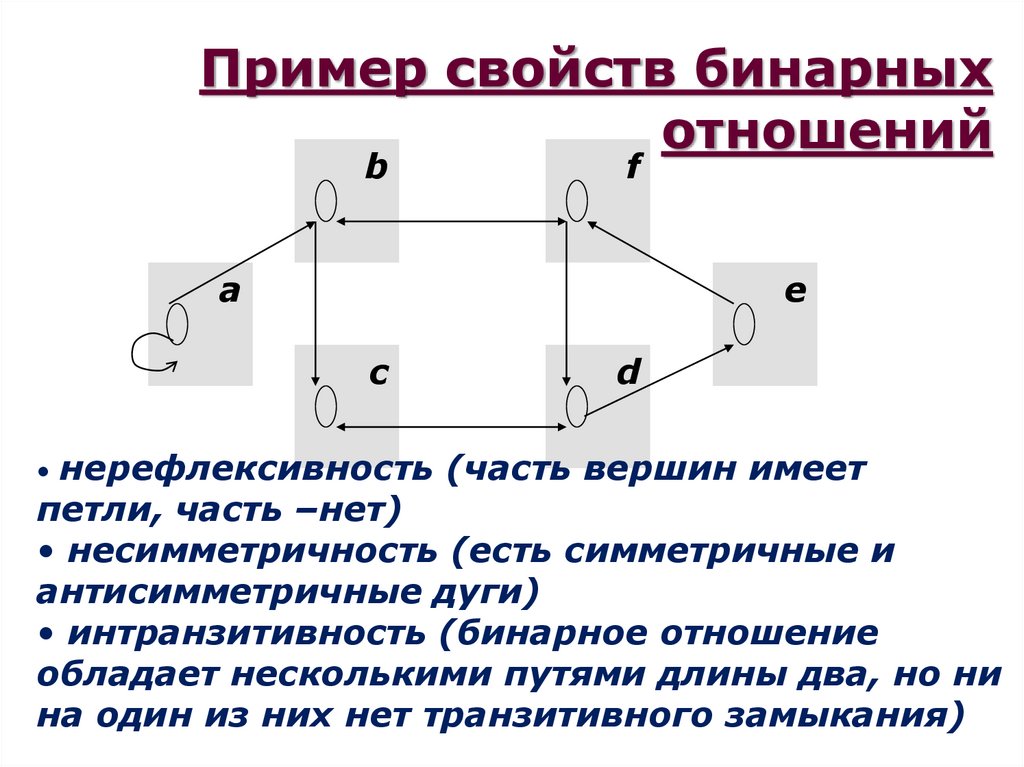
24. Пример свойств бинарных отношений

b
f
a
e
c
d
нерефлексивность (часть вершин имеет
петли, часть –нет)
• несимметричность (есть симметричные и
антисимметричные дуги)
• интранзитивность (бинарное отношение
обладает несколькими путями длины два, но ни
на один из них нет транзитивного замыкания)

25. Основные виды бинарных отношений.

Бинарное отношение R называется
отношением эквивалентности, если оно
одновременно обладает тремя свойствами:
рефлективностью, симметричностью и
транзитивностью, т.е. если для любых х, у, z
выполняется:
• xRx (рефлективность);
• если xRy, то уRх (симметричность);
• если xRy, a yRz, то xRz (транзитивность).

26.

Отношение толерантности
рефлексивность
симметричность
Отношения
«быть
другом»,
«быть
знакомым»,
- отношения толерантности, так
как они рефлексивны, симметричны, но не
транзитивны.
Отношение «иметь непустое пересечение»
для множеств – отношение толерантности.

27.

Отношение доминирования
антирефлексивность
Отношение
доминирования.
антирефлексивности
и
антисимметричность
Отношение,
антисимметричности,
наделенное
называют
свойствами
отношением
доминирования.
Отношение «быть начальником» - отношение
доминирования, так как оно рефлексивно,
симметрично, но не транзитивно.

28.

Отношение эквивалентности
рефлексивность
симметричность
транзитивность
Примеры отношений эквивалентности:
Отношение «быть равным на множестве
чисел», быть подобным на множестве
геометрических фигур.
Обозначение эквивалентных отношений:
a Q b или а ~ b, что означает «а эквивалентно b
в отношении Q»

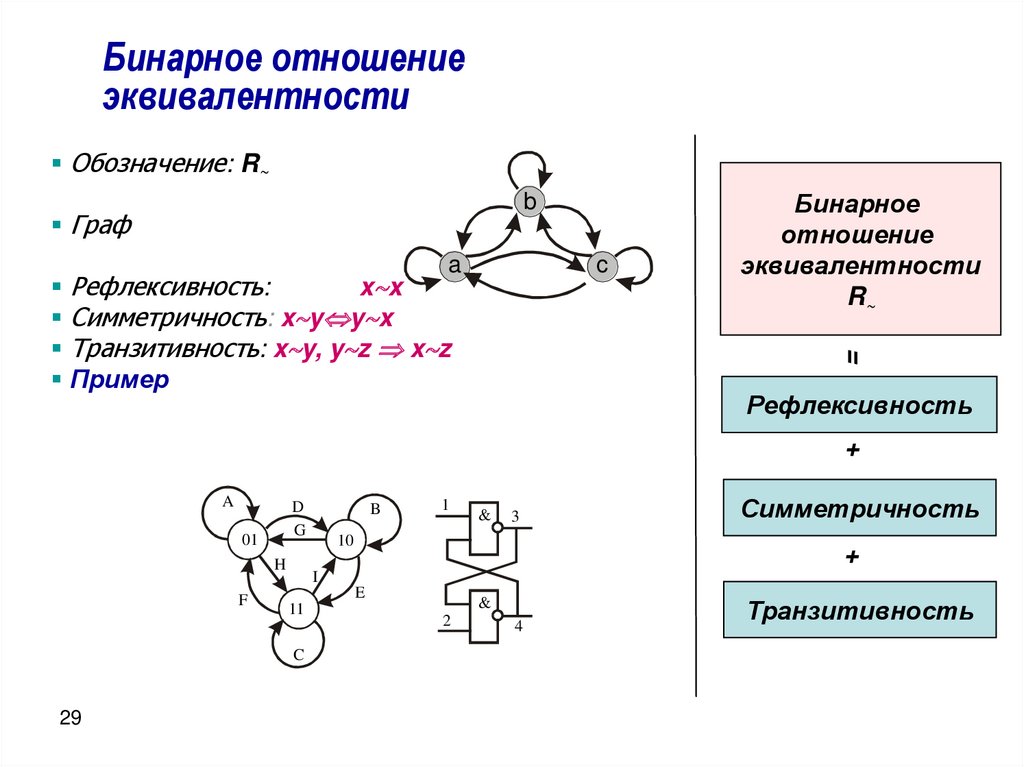
29.

Бинарное отношение
эквивалентности
Обозначение: R~
b
Граф
a
c
=
Рефлексивность:
x x
Симметричность: x y y x
Транзитивность: x y, y z x z
Пример
Бинарное
отношение
эквивалентности
R~
Рефлексивность
+
A
D
G
01
H
F
1
&
3
10
Симметричность
+
I
E
11
C
29
B
&
2
4
Транзитивность

30. Отношения

31. Отношения

32. Отношения

33. Отношение эквивалентности

34. Примеры отношений эквивалентности:

• отношение подобия в множестве треугольников в
евклидовой плоскости;
• отношение равенства в произвольной системе
множеств;
• отношение равночисленности, т.е. иметь
одинаковое число элементов, в системе конечных
множеств;
• отношение равносильности в множестве формул
логики высказываний;
• отношение «учиться в одной группе» в
множестве студентов факультета кибернетики;
9

35. Примеры отношений эквивалентности

36. Примеры отношений эквивалентности

37. Примеры отношений эквивалентности

38. Примеры отношений эквивалентности

39. «Антипримеры» отношений эквивалентности

40. «Антипримеры» отношений эквивалентности

41. Классы эквивалентности

42.

Разбиение множества
Def: разбиение Г множества А –
семейство непустых попарно
непересекающихся подмножеств,
объединение которых совпадает с А
Свойства Г В(А)
Ki Ã: Ki
Ki, Kj Г: Ki Kj =
Пример
Для трехэлементного
множества
A={a,b,c} разбиениями
являются
Г1={ {a, b, c} }
Г2={ {a}, {b}, {c} }
Г3={ {a}, {b,c} }
Г4={ {b}, {a,c} }
Г5={ {c}, {a,b} }
Kj A
K j
42

43.

Непересекающиеся
подмножества,
на
которые разбивается множество М отношением
эквивалентности,
называются
классами
эквивалентности.
На множестве обыкновенных дробей все
классы
эквивалентности
по
отношению
равенства состоят из дробей, равных по своей
величине.
На множестве треугольников все классы
эквивалентности по отношению подобия
состоят из треугольников, подобных между
собой.

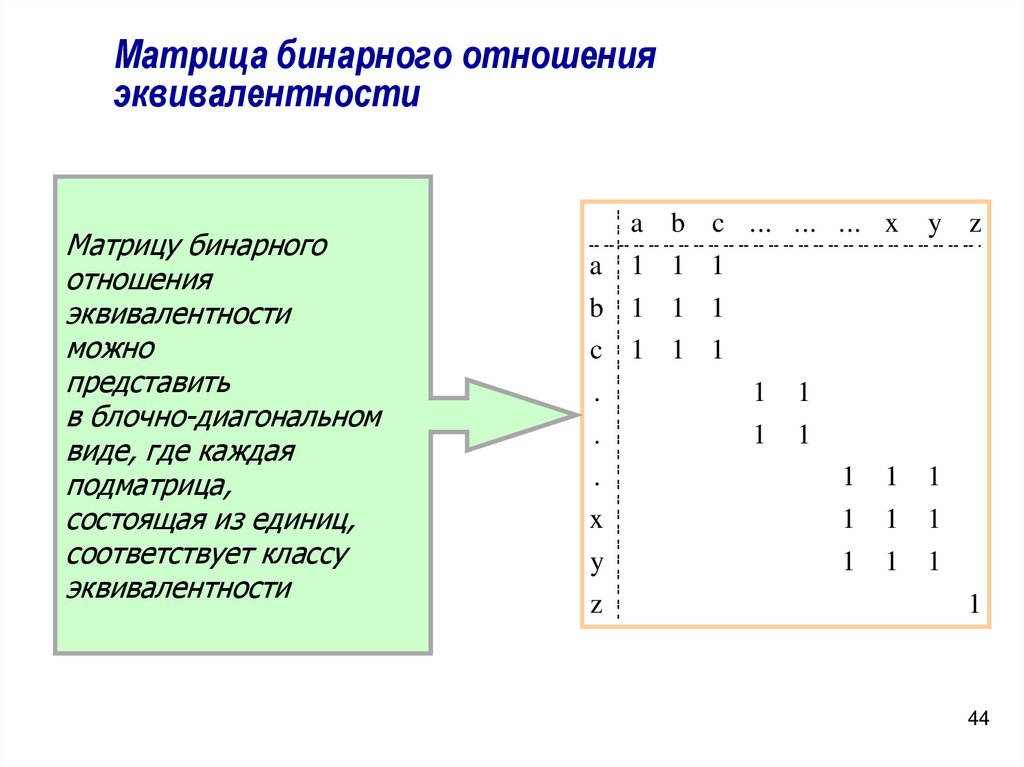
44.

Матрица бинарного отношения
эквивалентности
Матрицу бинарного
отношения
эквивалентности
можно
представить
в блочно-диагональном
виде, где каждая
подматрица,
состоящая из единиц,
соответствует классу
эквивалентности
a b c ... ... ... x
a
y z
1 1 1
b 1 1 1
c 1 1 1
.
1
1
.
1
1
.
1
1 1
x
1
1 1
y
1
1 1
z
1
44

45.

Отношение порядка
антисимметричность
транзитивность
Множество М, которое обладает отношением
порядка, называется упорядоченным.
+ рефлексивность
Отношение
нестрогого порядка
≤
+ антирефлексивность
Отношение
строгого порядка <

46.

Отношение называется отношением полного
порядка, если сравнимы все элементы
множества, на котором задано это отношение.
Пример. Отношения «больше» и «меньше»
на множестве действительных чисел.
Отношение
называется
отношением
частичного порядка, если сравнимы не все
элементы множества, на котором задано это
отношение.
Пример. Отношение «быть подмножеством»
на множестве В(U) (булеан).

47. Отношение частичного порядка

48. Примеры частично упорядоченных множеств

49. Примеры частично упорядоченных множеств

50. Примеры частично упорядоченных множеств

51. «Антипример» частично упорядоченного множества

52. Отношение частичного порядка

53. Отношение частичного порядка

54. Пример линейно упорядоченного множества

55. «Антипример» линейно упорядоченного множества

56.

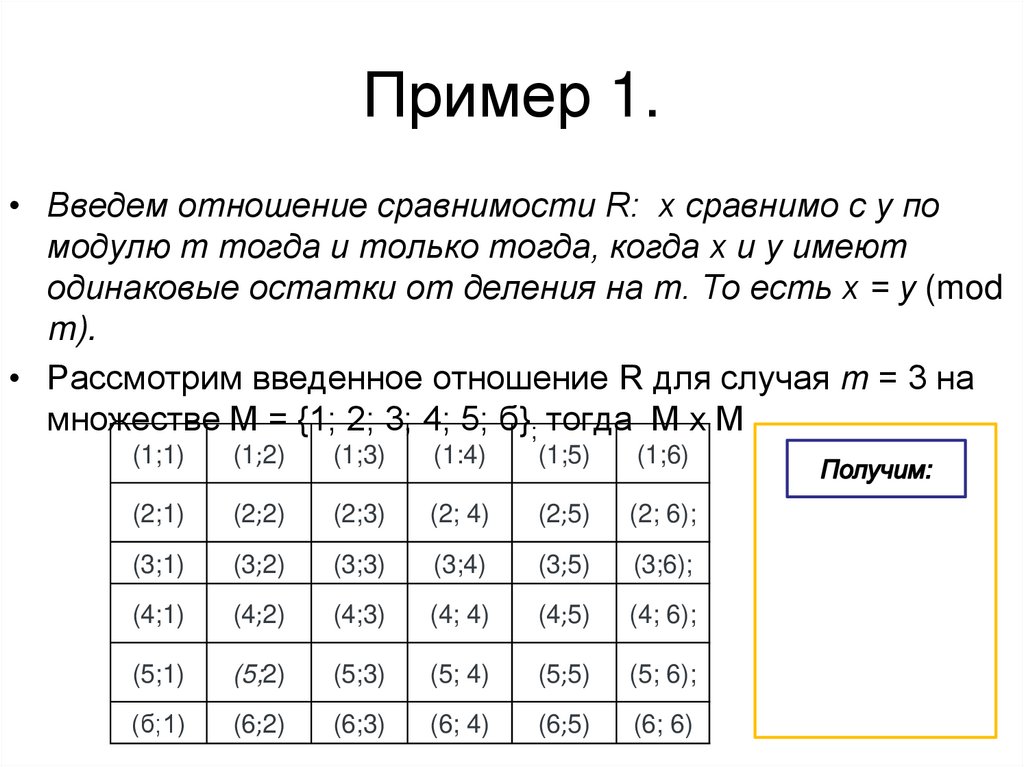
57. Пример 1.

• Введем отношение сравнимости R: х сравнимо с у по
модулю т тогда и только тогда, когда х и у имеют
одинаковые остатки от деления на т. То есть х = у (mod
m).
• Рассмотрим введенное отношение R для случая т = 3 на
множестве М = {1; 2; 3; 4; 5; б}; тогда М х М

58. Пример 1.

• Введем отношение сравнимости R: х сравнимо с у по
модулю т тогда и только тогда, когда х и у имеют
одинаковые остатки от деления на т. То есть х = у (mod
m).
• Рассмотрим введенное отношение R для случая т = 3 на
множестве М = {1; 2; 3; 4; 5; б}; тогда М х М
(1;1)
(1;2)
(1;3)
(1:4)
(1;5)
(1;6)
(2;1)
(2;2)
(2;3)
(2; 4)
(2;5)
(2; 6);
(3;1)
(3;2)
(3;3)
(3;4)
(3;5)
(3;6);
(4;1)
(4;2)
(4;3)
(4; 4)
(4;5)
(4; 6);
(5;1)
(5;2)
(5;3)
(5; 4)
(5;5)
(5; 6);
(б;1)
(6;2)
(6;3)
(6; 4)
(6;5)
(6; 6)

59. Пример 2.

На множестве М = {1; 2; 3; 4; 5; 6}
задано отношение делимости: xRy
тогда и только тогда, когда х делится на
у. Сколько пар содержит это
отношение? Перечислите эти пары.

60. Пример 3.

• Введем на множестве М = {1; 2; 3; 4; 5;
6} отношение взаимной простоты, т. е.
xRy тогда и только тогда, когда х и у
взаимно просты: D(x;y) = 1. Сколько пар
содержит это отношение? Перечислите
эти пары.

61. Контрольные вопросы:

1. Что понимается под соответствием между
множествами?
2. Какое отношение называется бинарным?
3. Какое бинарное отношение называется
рефлексивным? Приведите пример.
4. Какое бинарное отношение называется
антирефлексивным? Приведите пример.
5. Какое бинарное отношение называется
симметричным? Приведите пример.
6. Какое бинарное отношение называется
асимметричным? Приведите пример.
7. Какое бинарное отношение называется
антисимметричным? Приведите пример.
8. Какое бинарное отношение называется транзитивным?
Приведите пример.

62. Упражнения

• 1. Укажите, какие отношения из указанных
являются рефлексивными,
симметричными и транзитивными на
множестве натуральных чисел:
а) R= (х, y) х у ;
б) R= (х, y) у делится без остатка на х ;
в) R= (х, y) х и у при делении на 3 дают
остаток 2 .

63. Упражнения

• 2. Укажите, какие отношения из
указанных являются рефлексивными,
симметричными и транзитивными на
множестве векторов:
а) R= (х, y) х коллинеарен у ;
б) R= (х, y) х у ;
в) R= (х, y) х = 2у .

64. Свойства бинарных отношений