Уравнения и неравенства с одной переменной

1.

2.

Цели и задачи:
повторить, обобщить и закрепить знания
учащихся по данной теме;
подготовить учащихся к выполнению
контрольной работы;
воспитывать умение слушать отвечающего,
дополнять ответ и отстаивать свое мнение, если
ты прав;
развивать логическое мышление, быстроту и
смекалку при решении упражнений.

3.

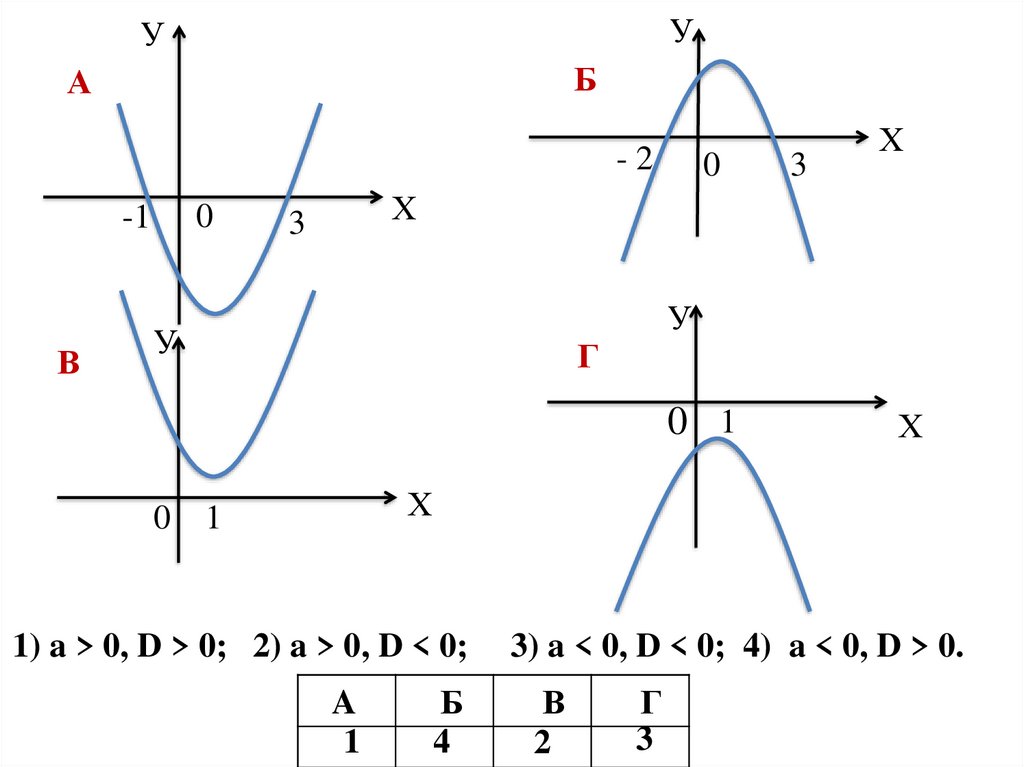
1. Функция f(х) = ах² + bх + с задана
графически.
D – дискриминант
соответствующего квадратного
трехчлена. Соотнесите графики с
ответами и заполните таблицу,
проставив в ней номера ответов.

4.

У
У
Б
А
-2
0
-1
В
0
Х
3
У
У
Г
0 1
0
3
Х
Х
Х
1
1) a > 0, D > 0; 2) a > 0, D < 0;
A
1
Б
4
3) a < 0, D < 0; 4) a < 0, D > 0.
В
2
Г
3

5.

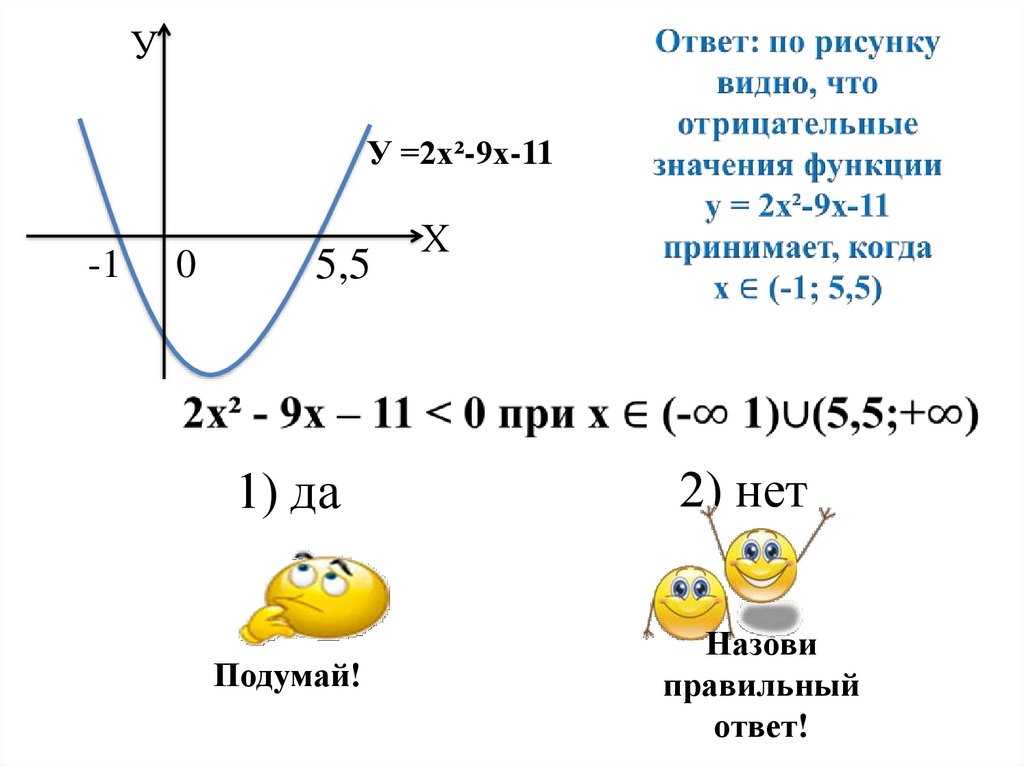
2. На рисунках изображены схематически
графики функций, и с помощью этих
графиков решены неравенства. Определите,
верно ли они решены, выбрав ответ да или
нет. Если решение неверное, надо дать
правильный ответ.

6.

У
У =2х²-9х-11
-1
0
5,5
1) да
Подумай!
Х
2) нет
Назови
правильный
ответ!

7.

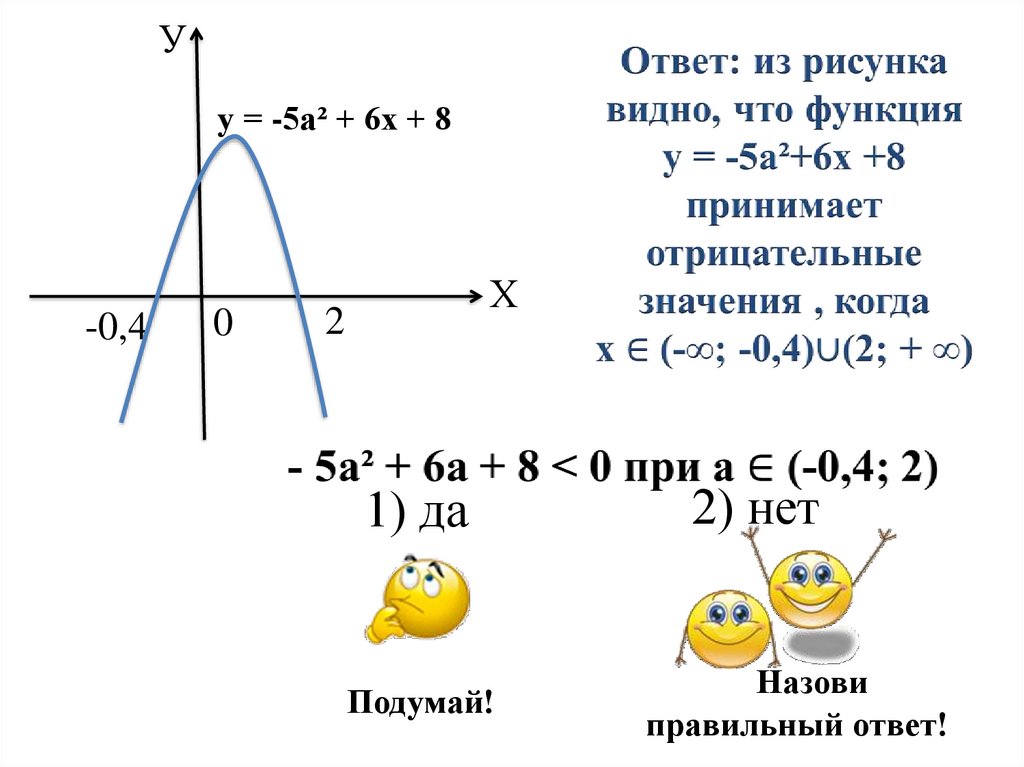
У
у = -5а² + 6х + 8
-0,4
0
Х
2
1) да
Подумай!
2) нет
Назови
правильный ответ!

8.

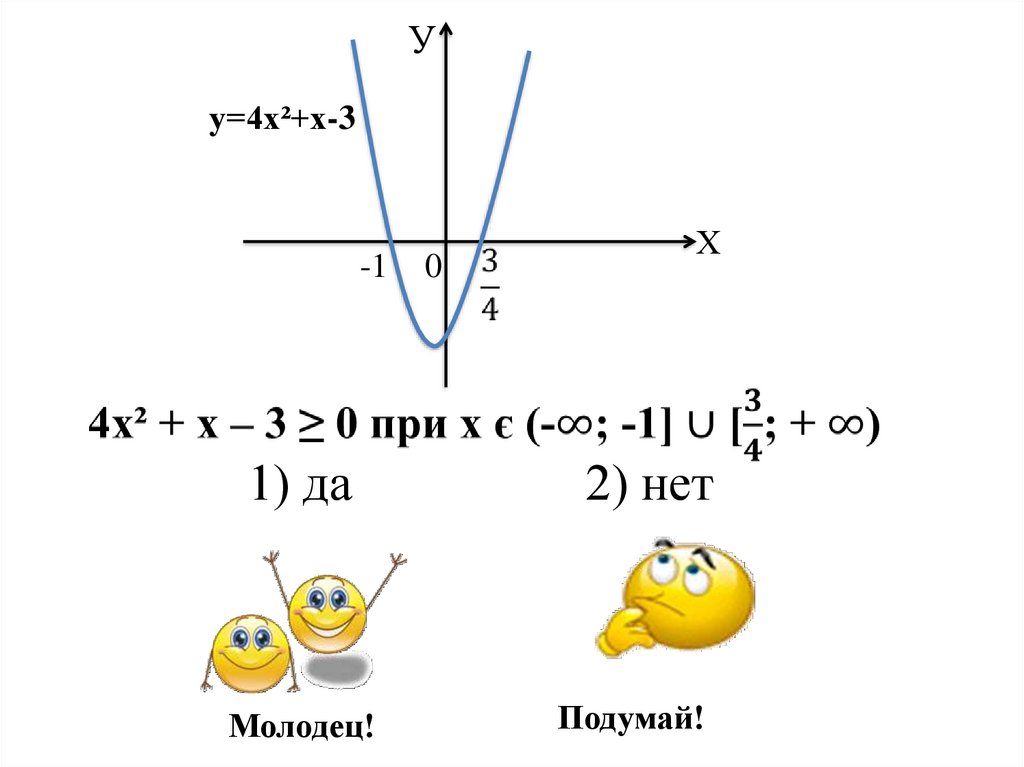
У
у=4х²+х-3
-1
1) да
Молодец!
0
Х
2) нет
Подумай!

9.

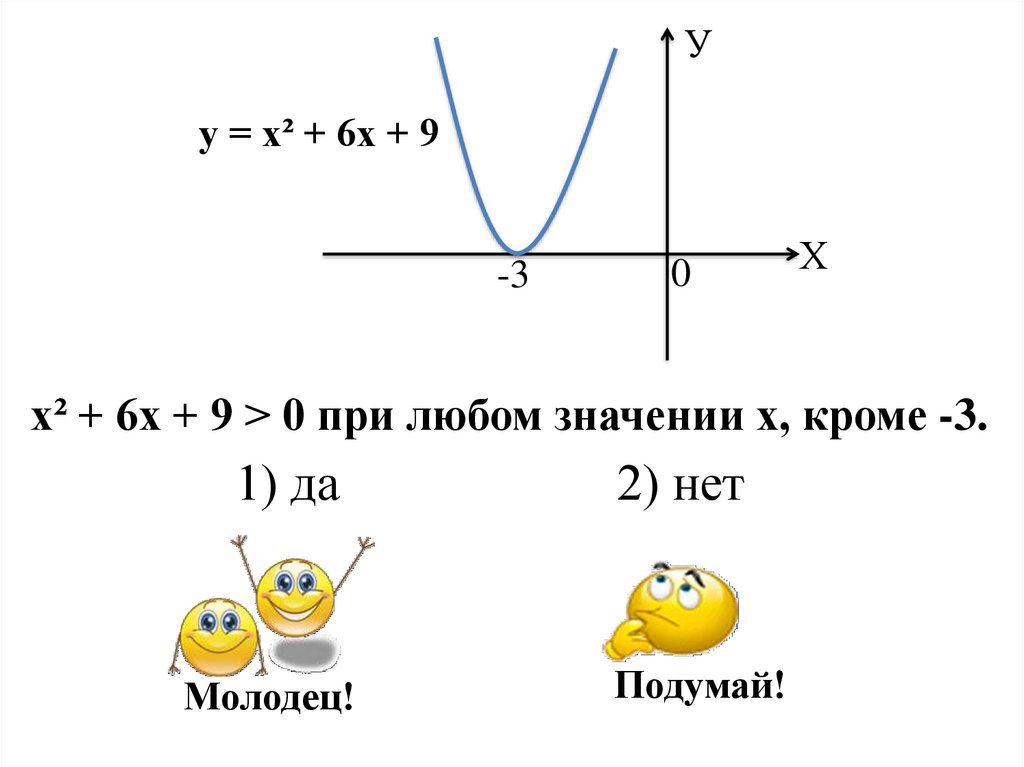
У
у = х² + 6х + 9
-3
0
Х
х² + 6х + 9 > 0 при любом значении х, кроме -3.
1) да
Молодец!
2) нет
Подумай!

10.

У
0
2
-2
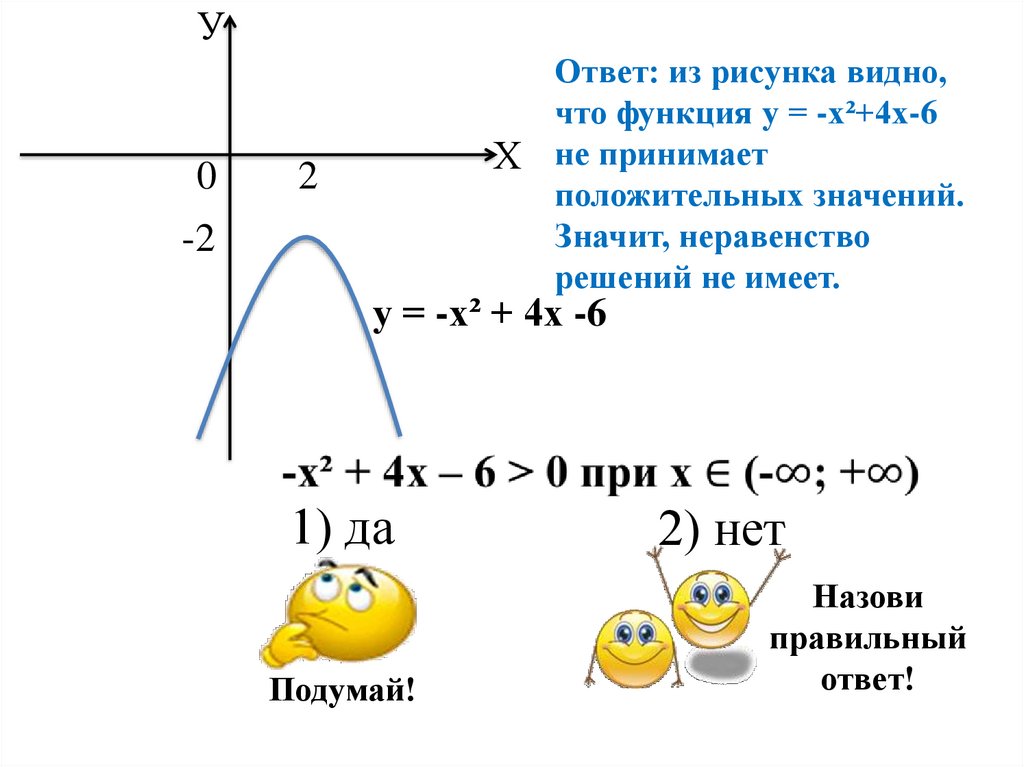
Ответ: из рисунка видно,
что функция у = -х²+4х-6
Х не принимает
положительных значений.
Значит, неравенство
решений не имеет.
у = -х² + 4х -6
1) да
Подумай!
2) нет
Назови
правильный
ответ!

11.

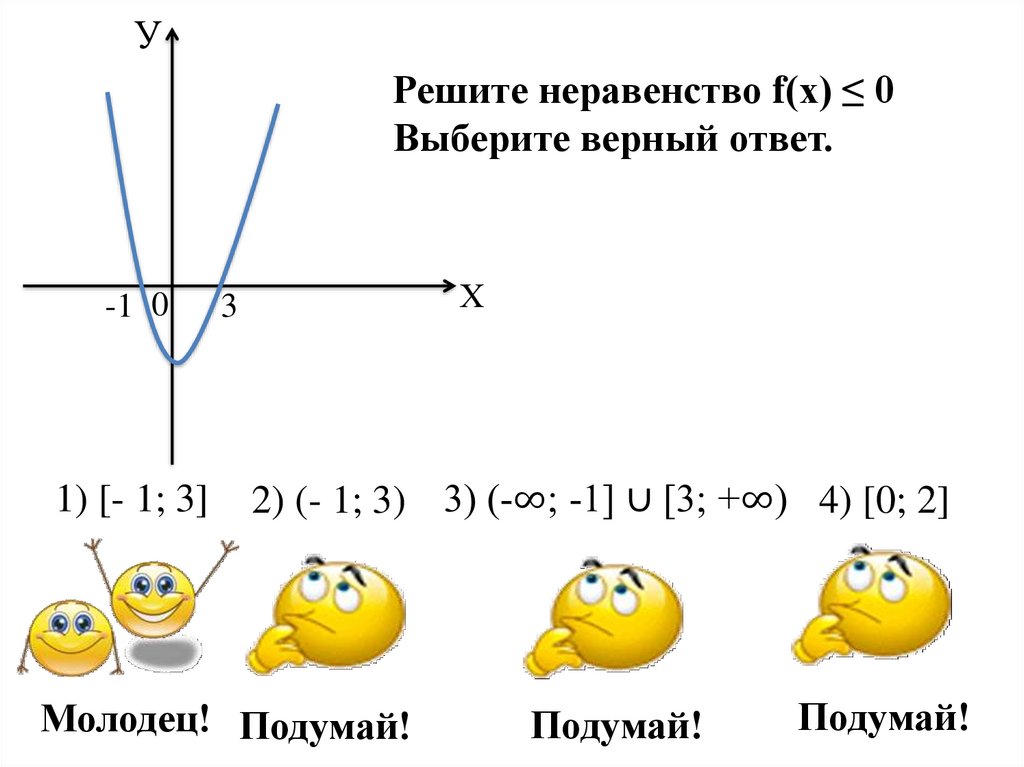
У
Решите неравенство f(х) ≤ 0
Выберите верный ответ.
-1 0
1) [- 1; 3]
Х
3
2) (- 1; 3)
Молодец! Подумай!
4) [0; 2]
Подумай!
Подумай!

12.

У
-2
0
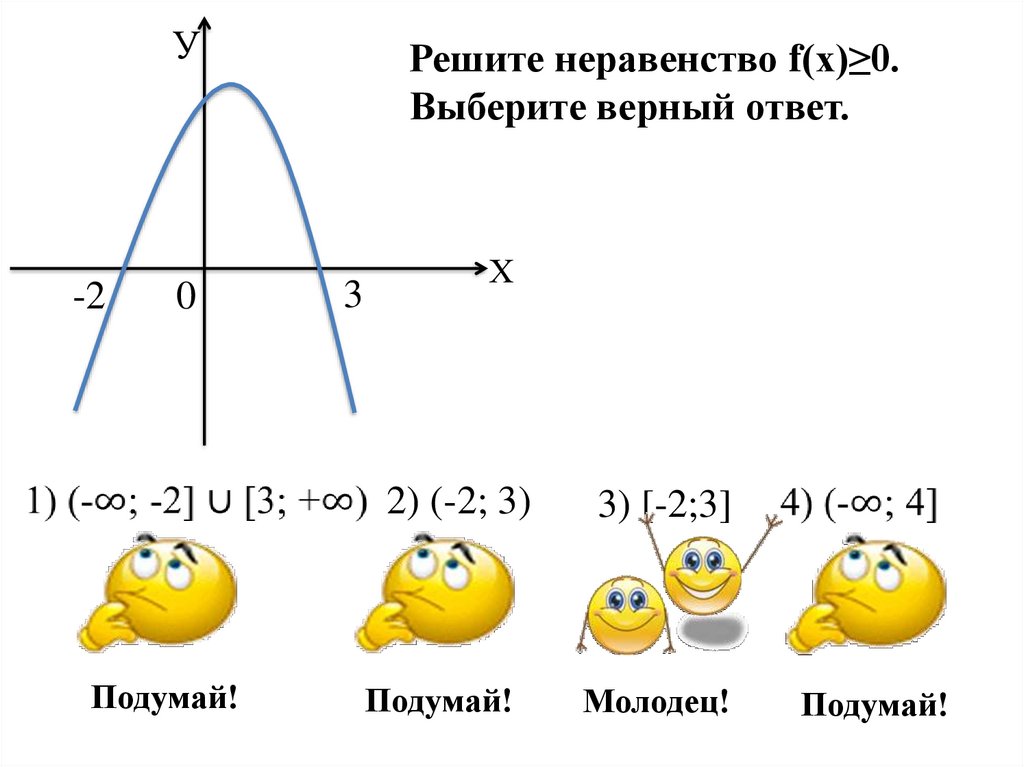
Решите неравенство f(х)≥0.
Выберите верный ответ.
3
Х
2) (-2; 3)
Подумай!
Подумай!
3) [-2;3]
Молодец!
Подумай!

13.

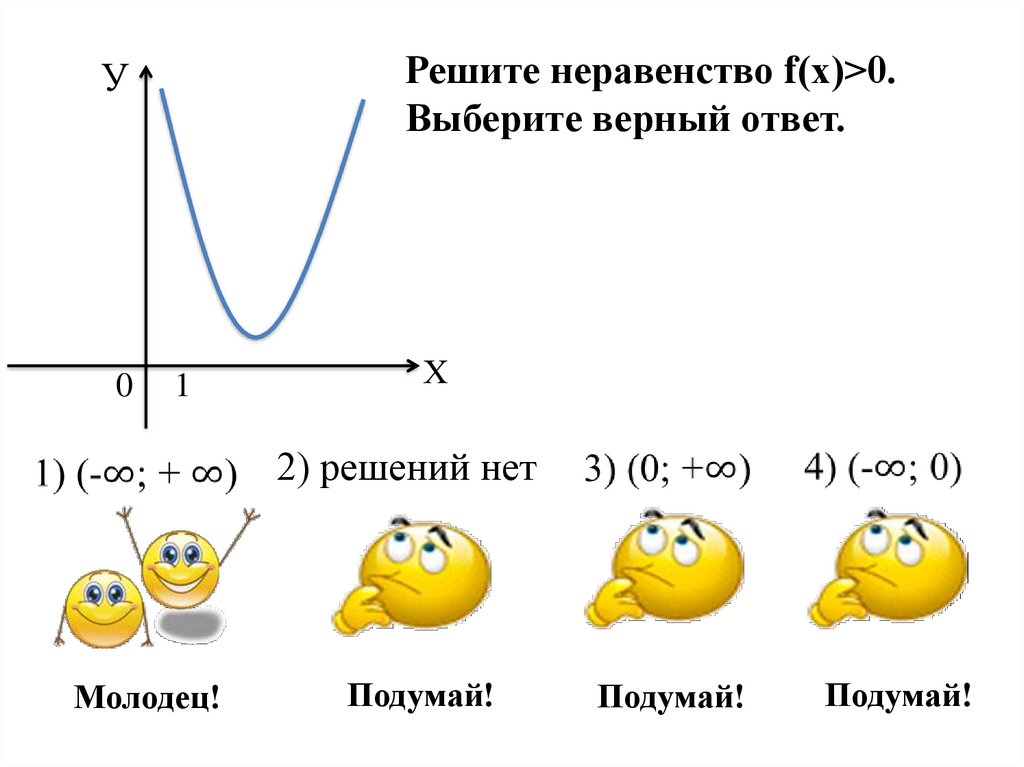
Решите неравенство f(х)>0.
Выберите верный ответ.
У
0
1
Х
2) решений нет
Молодец!
Подумай!
Подумай!
Подумай!

14.

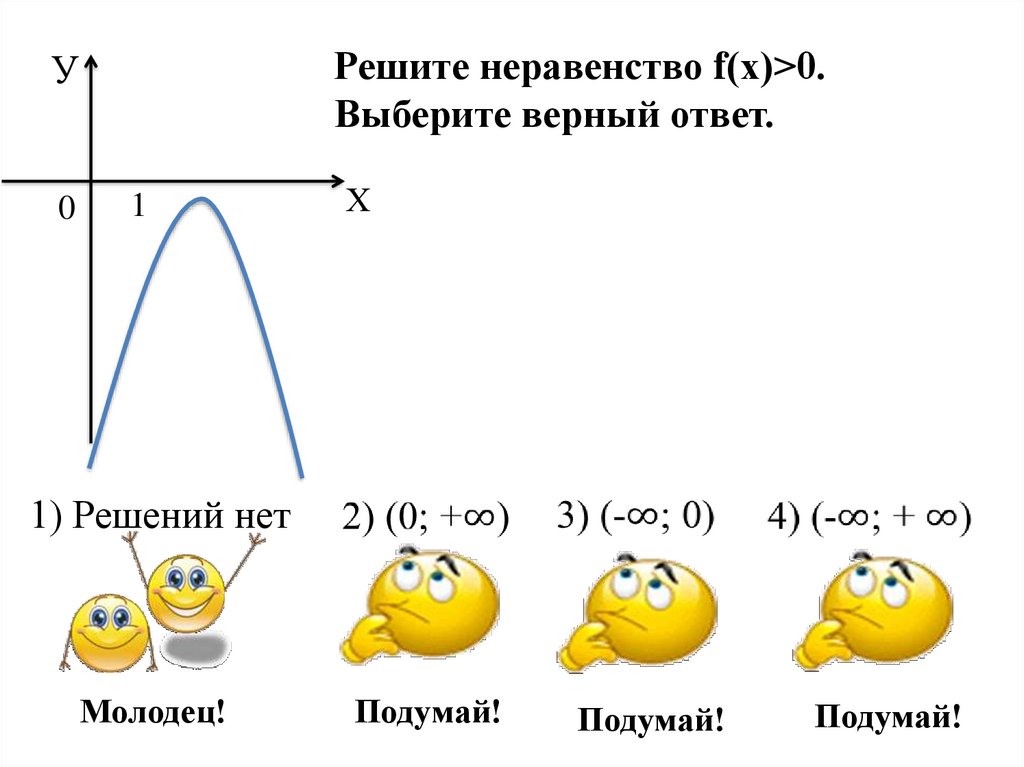
Решите неравенство f(х)>0.
Выберите верный ответ.
У
0
1
Х
1) Решений нет
Молодец!
Подумай!
Подумай!
Подумай!

15.

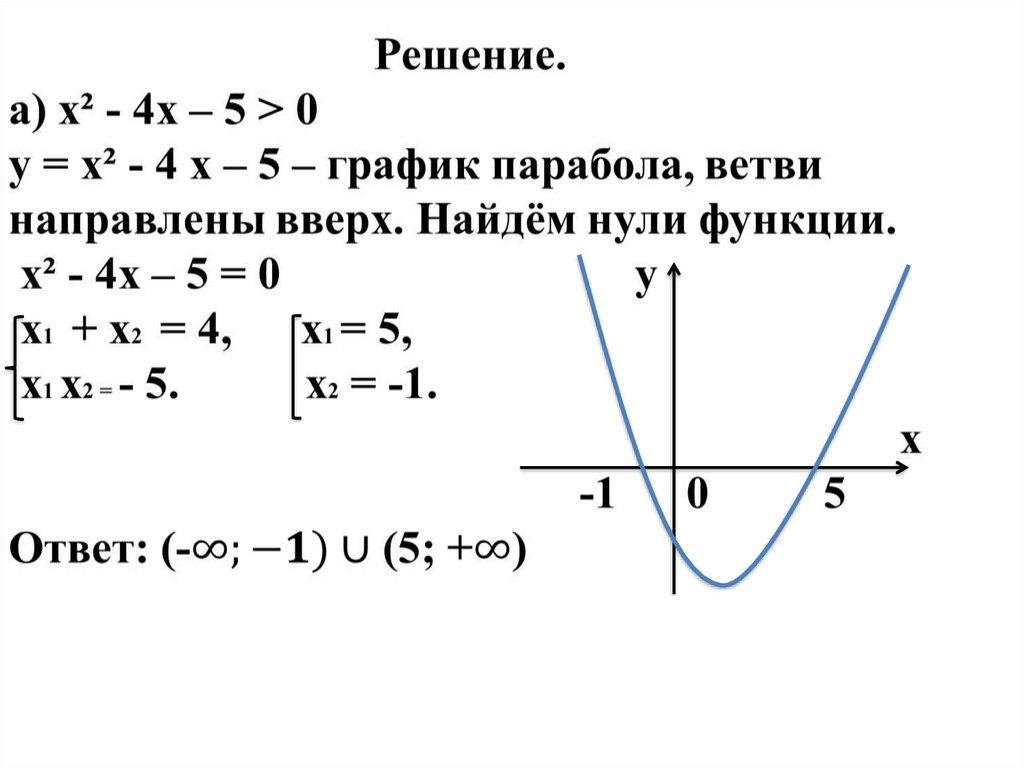
1. Решите неравенства.
а) х² - 4х – 5 > 0;
б) - х² + 8х – 15 ≥ 0.

16.

17.

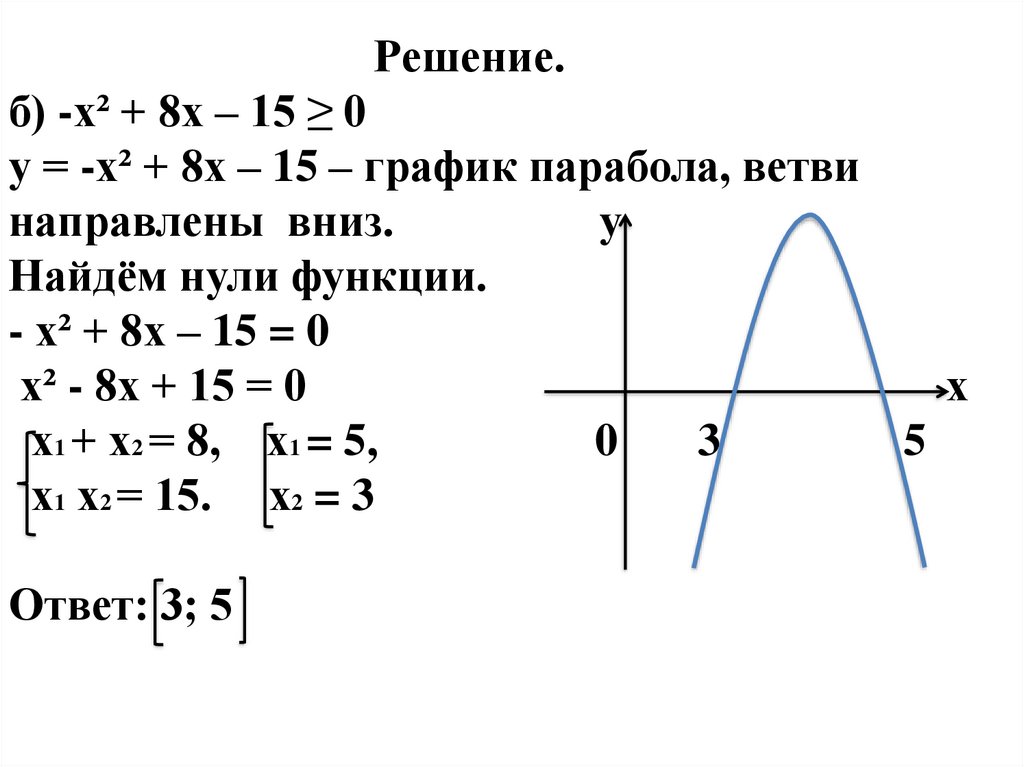
Решение.
б) -х² + 8х – 15 ≥ 0
у = -х² + 8х – 15 – график парабола, ветви
направлены вниз.
у
Найдём нули функции.
- х² + 8х – 15 = 0
х² - 8х + 15 = 0
х
х1 + х2 = 8, х1 = 5,
0
3
5
х1 х2 = 15. х2 = 3
Ответ: 3; 5

18.

Решение неравенств методом интервалов.
Ученику 9 класса Петру Иванову учитель предложил
решить два неравенства методом интервалов. Он решил.
Учитель проверил и сказал ему, что у него есть ошибки в
ответах. Попросил его подумать и исправить.
Давайте, ребята, поможем Петру исправить ошибки.
2. Решите неравенства методом интервалов
а) (х + 2) (х – 7) > 0;
Ученик.
Решение.
а) (х + 2)(х – 7) > 0
Найдем нули функции у = (х + 2) (х – 7).
(х + 2)(х -7) = 0
+
Х + 2 = 0 или х – 7 = 0
-2
Х = -2
х=7
Ответ: (-2; 7)
+
7

19.

б)(х – 5) (х + 3)≤0
Решение.
Найдем нули функции f(х)= (х – 5) (х + 3)
(х – 5) (х + 3) = 0
х – 5 = 0 или х + 3 = 0
х=5
х=-3
+
-3
+
5
Ответ: ( -3; 5).
Правильный ответ: [-3; 5].

20.

1. Решите неравенство в ответ запишите наименьшее
целое решение неравенства
(х – 4) (3х +1) (х -2) > 0

21.

Учебно – методический комплект:
1. Учебник «Алгебра 9 класс». Авторы Ю. Н. Макарычев, Н. Г.
Миндюк, н, Г. Нешков, С. Б. Суворова. Москва «Просвещение»
2013год.
2. Дидактические материалы «Алгебра 9 класс». Авторы Ю. Н.
Макарычев, Н. Г. Миндюк, Л. М. Короткова. Москва «Просвещение»
2005 год.
3. Сборник тестовых заданий для тематического и обобщающего
контроля «Алгебра 9 класс». Автор Крайнева Л. Б. Москва
«Интеллект – Центр» 2007 год.
Интернет - ресурсы
http://smayls.ru/smayliki-emocii_12.html
http://overgraph.ru/smailik-animaciya/