Похожие презентации:
Четные и нечетные числа
1.
События1.Разминка
2.Учимся решать
3.Математический майнинг (группа)
4.Математический майнинг
(индивидуально)
5.Математический бой
2.
1.2.
3.
4.
5.
6.
Правила и установки группы
Каждый может стать учителем
Главное понять решение, а не узнать правильный ответ
Накопление знаний прямо пропорционально росту личного
капитала маткоинов
Тетрадь+ручка+каранадаш+линейка
Запрещено пользоваться телефоном
Запрещено списывать
3.
4.
РАЗМИНКА1)
2)
11
1
72
−
47
72
3
4
97 168
1,8:36+1,2:0,25−
:
160 24
7−6,35 :6,5+4
: 1,25 +
15
40
: 0,358 − 0,108 ∙
19
1,6 −
25
5.
ЧЁТНОСТЬ6.
СВОЙСТВА ЧЁТНОСТИ ДЛЯ ЦЕЛЫХ ЧИСЕЛ1.
2.
3.
4.
5.
6.
7.
8.
9.
Сумма чётных чисел чётна.
Сумма двух нечётных чисел чётна.
Сумма чётного и нечётного чисел нечётна.
Произведение любого числа на чётное — чётно.
Если произведение нечётно, то все сомножители нечётны.
Сумма чётного количества нечётных чисел чётна.
Сумма нечётного количества нечётных чисел нечётна.
Разность и сумма двух данных чисел — числа одной чётности.
Если объекты можно разбить на пары, то их количество чётно.
7.
Задача 1Кузнецу заказали выковать десять мечей. Каждый
меч может стоить 3, 5 или 7 златников. Могут ли они
стоить в сумме 53 златника?
8.
Задача 2Можно ли 7 селений соединить между собой
попарно так, чтобы каждое было соединено
напрямую ровно с тремя другими?
9.
Задача 313 команд мечников участвуют в королевском однокруговом
турнире. Докажите, что в любой момент есть команда, сыгравшая
чётное число встреч. (Однокруговой турнир — когда каждая
команда играет с каждой ровно один раз.)
10.
Задача 4В секции фехтования мальчиков в 14 раз больше, чем девочек, при
этом всего в секции не более 20 человек. Смогут ли они разбиться
на пары?
11.
Чётность как инвариантИнвариант — неизменяемость.
Инвариант — это характеристика некоторого класса
(множества) математических объектов быть неизменными при
преобразованиях конкретного типа.
12.
Задача 5Казначей положил на стол 6 монет, одну из них вверх
орлом, другие — решкой. Можно ли все монеты положить
вверх орлом, если разрешено одновременно
переворачивать две монеты?
13.
Задача 6Можно ли в таблице 5*5 расставить 25 натуральных
чисел, чтобы во всех строках суммы были чётные, а
во всех столбцах — нечётные?
14.
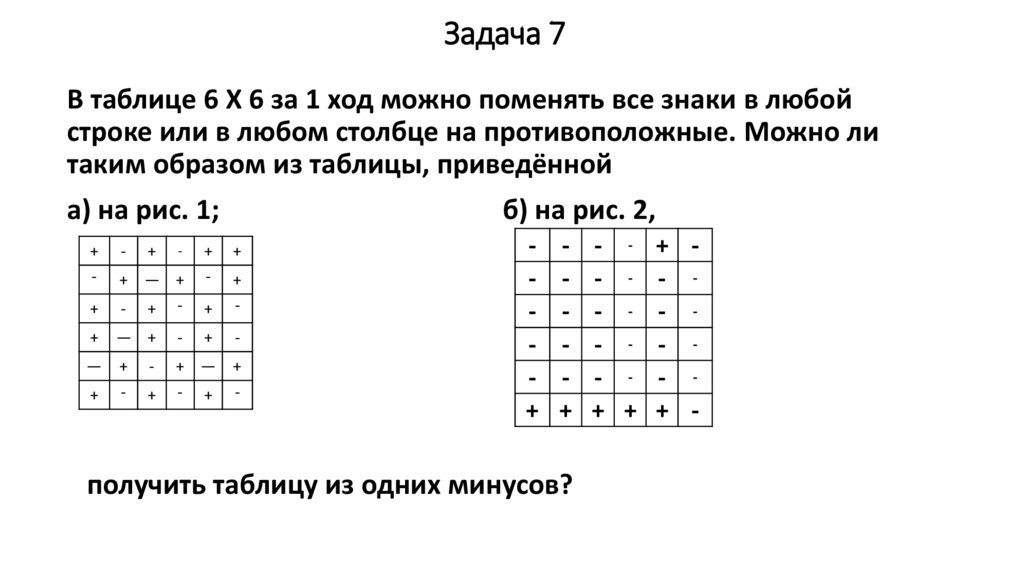
Задача 7В таблице 6 X 6 за 1 ход можно поменять все знаки в любой
строке или в любом столбце на противоположные. Можно ли
таким образом из таблицы, приведённой
а) на рис. 1;
+
-
-
+
-
+
-
б) на рис. 2,
+
+
+ — +
- + -
+
— +
-
—
+
-
+ — +
- + -
+
+
+
+
-
+
-
+
+
получить таблицу из одних минусов?
- - - - - + +
+ - - - - + -
15.
Задача 8На столе стоят 16 кубков, один из них вверх дном.
Можно ли все кубки поставить правильно, если
можно одновременно переворачивать по 4 кубка?
16.
Чётность суммы и произведения чиселЗадача 9
На доске написаны числа 1, 2, 3, ..., 2017, 2018. Разрешается
стереть с доски любые два числа и вместо них записать модуль их
разности. В конце концов на доске останется одно число. Может ли
оно равняться нулю?
17.
Задача 10На доске написаны числа 12, 22, З2, N2. Между ними произвольным
образом расставляют знаки + и — и находят получившуюся сумму.
Может ли такая сумма равняться:
а) 12, если N = 12?
б) 0, если N = 70?
18.
Задача 11На доске написаны последовательные натуральные числа от 1 до
2015, разрешается за одну операцию любые два числа стереть и
вместо них поставить их произведение. Какое наибольшее число
операций можно сделать, прежде чем все числа на доске станут
чётными? Какое наименьшее?

















 Математика
Математика








