Похожие презентации:
Применение производной к исследованию функций. Возрастание и убывание функции
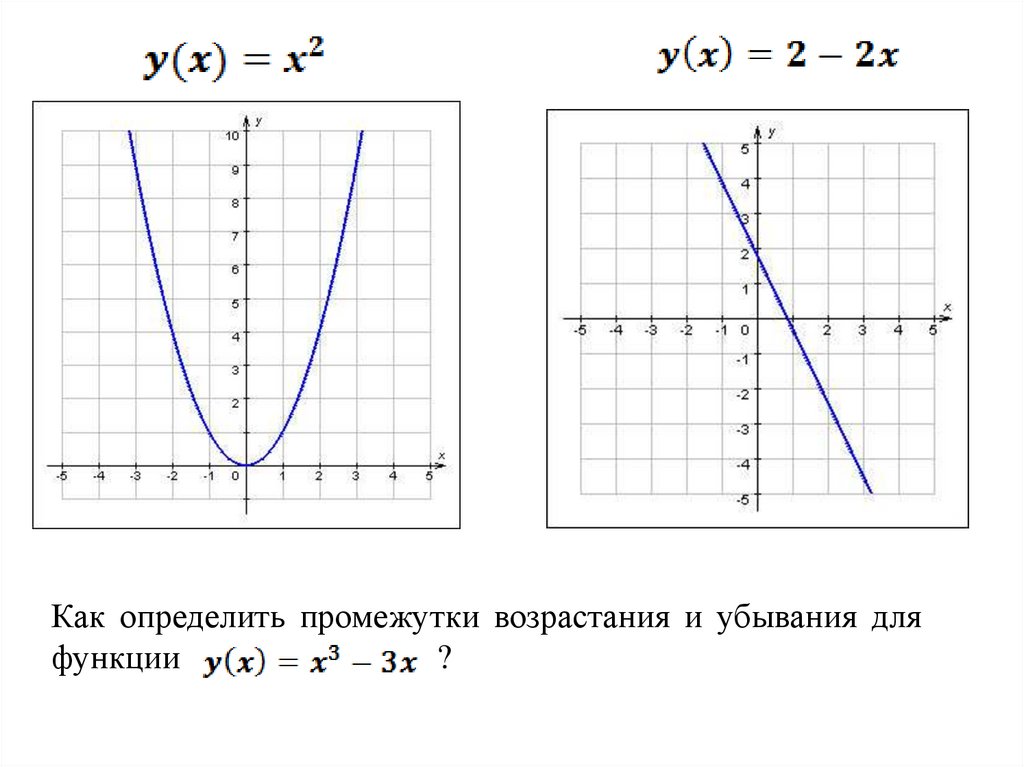
1.
2.
Как определить промежутки возрастания и убывания дляфункции
?
3.
4.
Достаточный признак убывания функцииЕсли f‘(x)<0 в каждой точке интервала (а;b),
то функция f убывает на интервале (а;b).
Достаточный признак возрастания функции
Если f‘(x)>0 в каждой точке интервала (а;b),
то функция f возрастает на интервале (а;b).
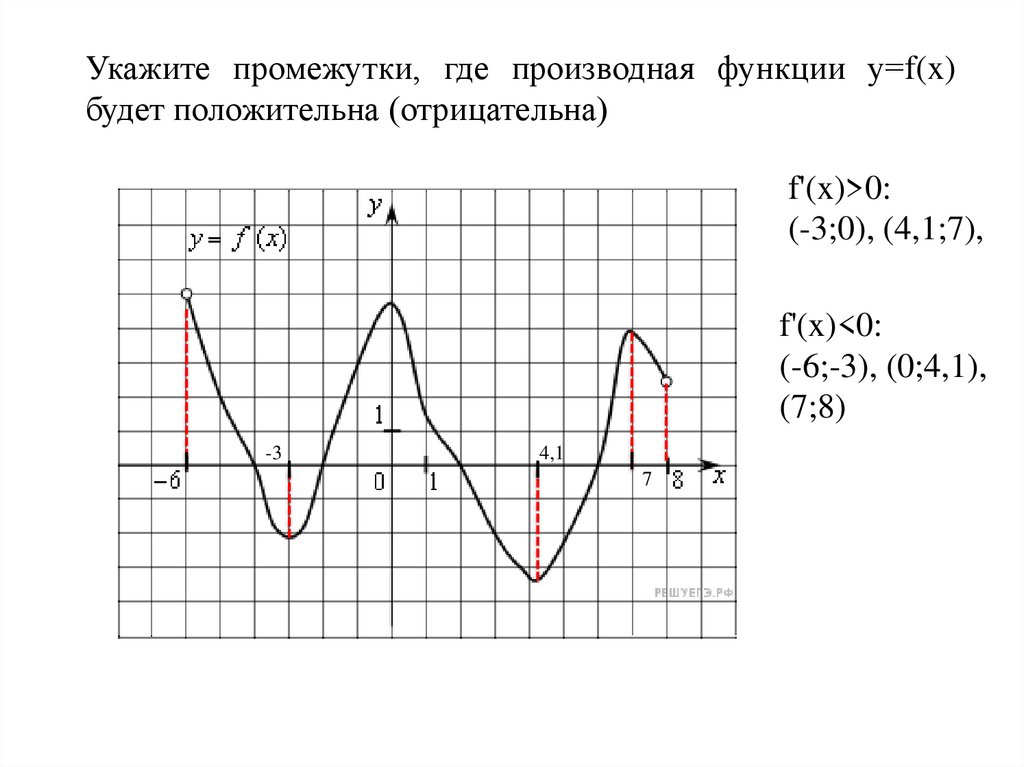
5.
Укажите промежутки, где производная функции у=f(x)будет положительна (отрицательна)
f'(x)>0:
(-3;0), (4,1;7),
у=f(x)
f'(x)<0:
(-6;-3), (0;4,1),
(7;8)
-3
4,1
7
6.
1.Найти область определения функции – D(f).2.Вычислить производную функции – f ' (х).
3.Найти точки, в которых производная равна нулю или не существует.
4.Отметить в области определения функции точки,
в которых производная равна нулю или не существует.
5.Расставить знаки производной в каждом из полученных промежутков.
6.Определить промежутки возрастания и убывания функции f(х).
7. Записать ответ.
7.
ЗАДАНИЕ 1. f ( x) 2 x 3 3x 2 12 x 81) D f ( ; )
2) f 6 x 2 6 x 12
3)6 x 2 6 x 12 0
x2 x 2 0
x1 x2 1
x1 x2 2
-
+
-2
Ответ: функция f(х) возрастает на
(-∞;-2), (1;∞)
функция f(х) убывает на (-2;1)
+
1
x1 1
x2 2
f ( 5) 0
f (0) 0
f ( 2) 0
8.
1 3ЗАДАНИЕ 2. f ( x )
x 4 x 2 12 x 18
3
1) D f ( ; )
2) f x 2 8 x 12
3) x 2 8 x 12 0
x1 x2 8
x1 x2 12
-
+
2
Ответ: функция f(х) убывает на
(2;6)
+
6
x1 6
x2 2
f (7 ) 0
f (3) 0
f (0) 0
9.
Задание 3Задание 4
Найти промежутки
возрастания функции
Найти промежутки
убывания функции








 Математика
Математика








