Параллельность в пространстве

1. Параллельность в пространстве

5 - 9 вопросы
к экзамену
по геометрии

2.

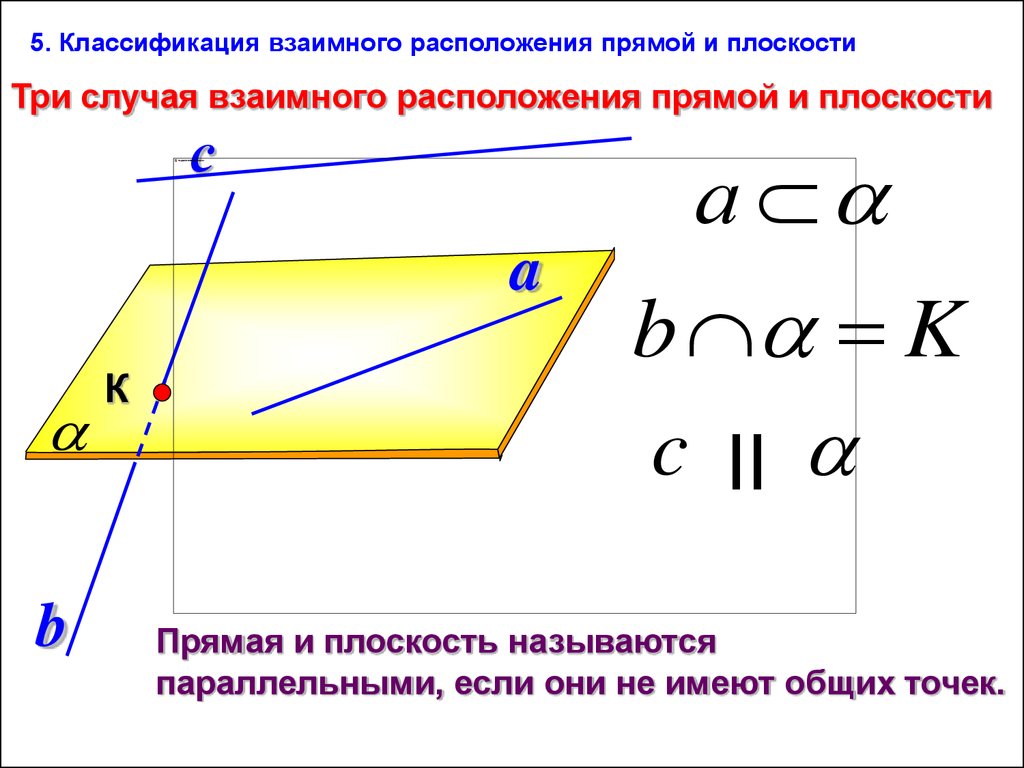
5. Классификация взаимного расположения прямой и плоскости
Три случая взаимного расположения прямой и плоскости
с
а
a
b
К
b K
c II
Прямая и плоскость называются
параллельными, если они не имеют общих точек.

3.

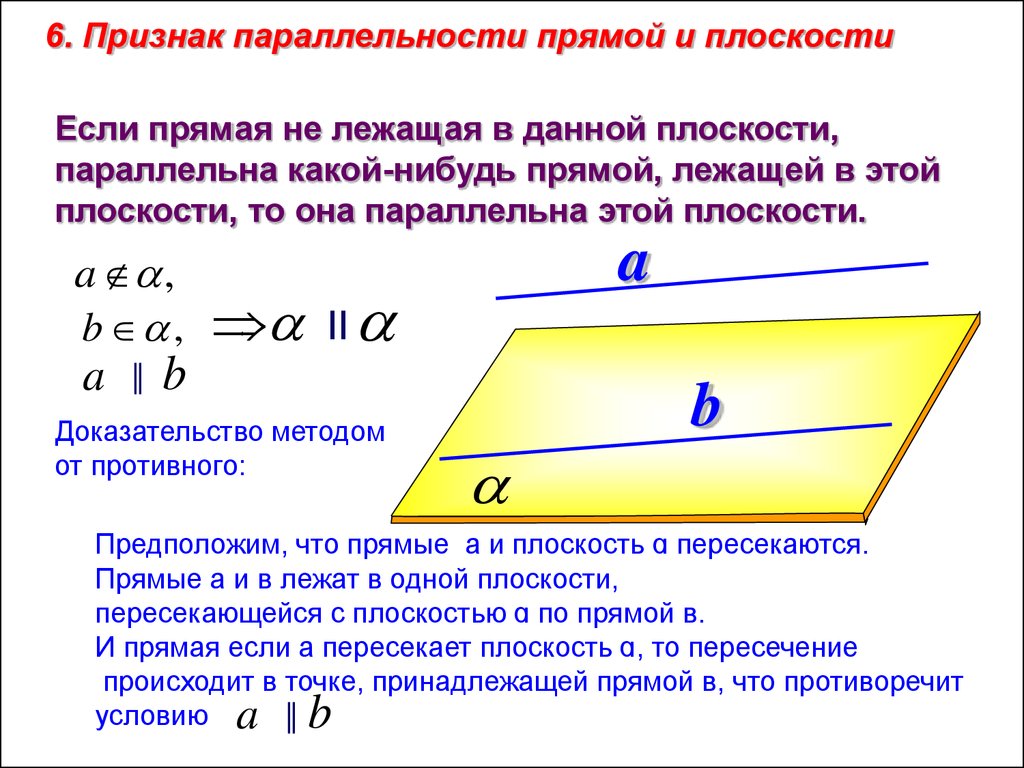
6. Признак параллельности прямой и плоскости
Если прямая не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой
плоскости, то она параллельна этой плоскости.
a ,
b ,
║
a
a
II
,
b
Доказательство методом
от противного:
b
Предположим, что прямые а и плоскость ɑ пересекаются.
Прямые а и в лежат в одной плоскости,
пересекающейся с плоскостью ɑ по прямой в.
И прямая если а пересекает плоскость ɑ, то пересечение
происходит в точке, принадлежащей прямой в, что противоречит
условию a
b
║

4.

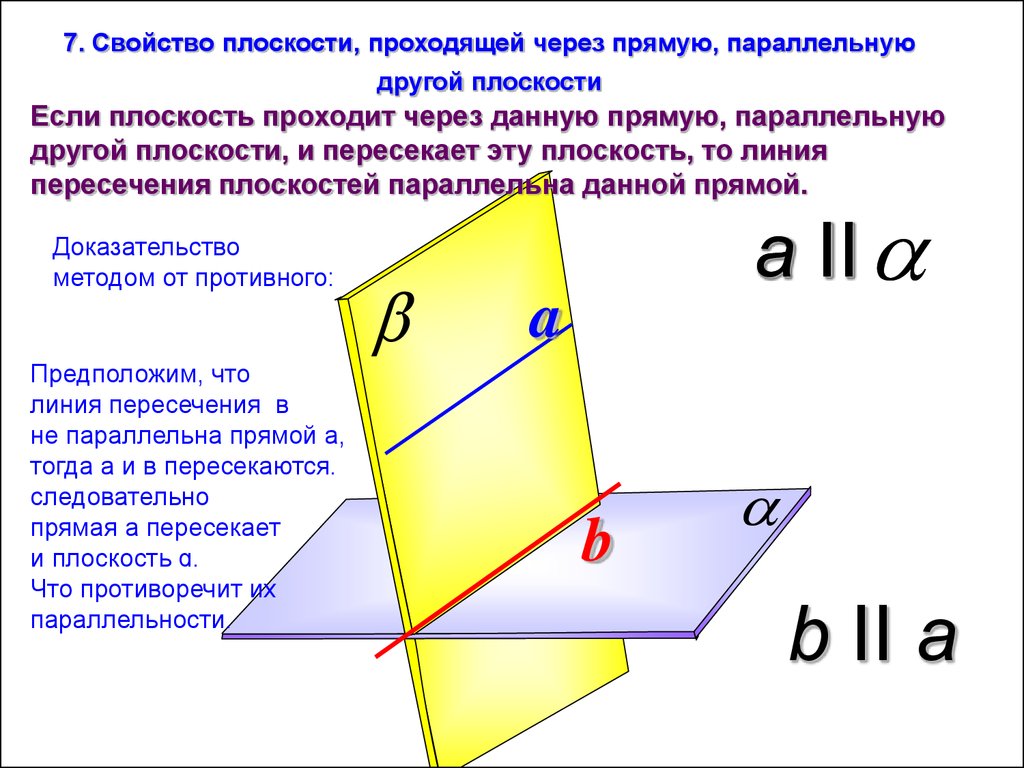
7. Свойство плоскости, проходящей через прямую, параллельную
другой плоскости
Если плоскость проходит через данную прямую, параллельную
другой плоскости, и пересекает эту плоскость, то линия
пересечения плоскостей параллельна данной прямой.
Доказательство
методом от противного:
Предположим, что
линия пересечения в
не параллельна прямой а,
тогда а и в пересекаются.
следовательно
прямая а пересекает
и плоскость ɑ.
Что противоречит их
параллельности.
a II
a
b
b II a

5.

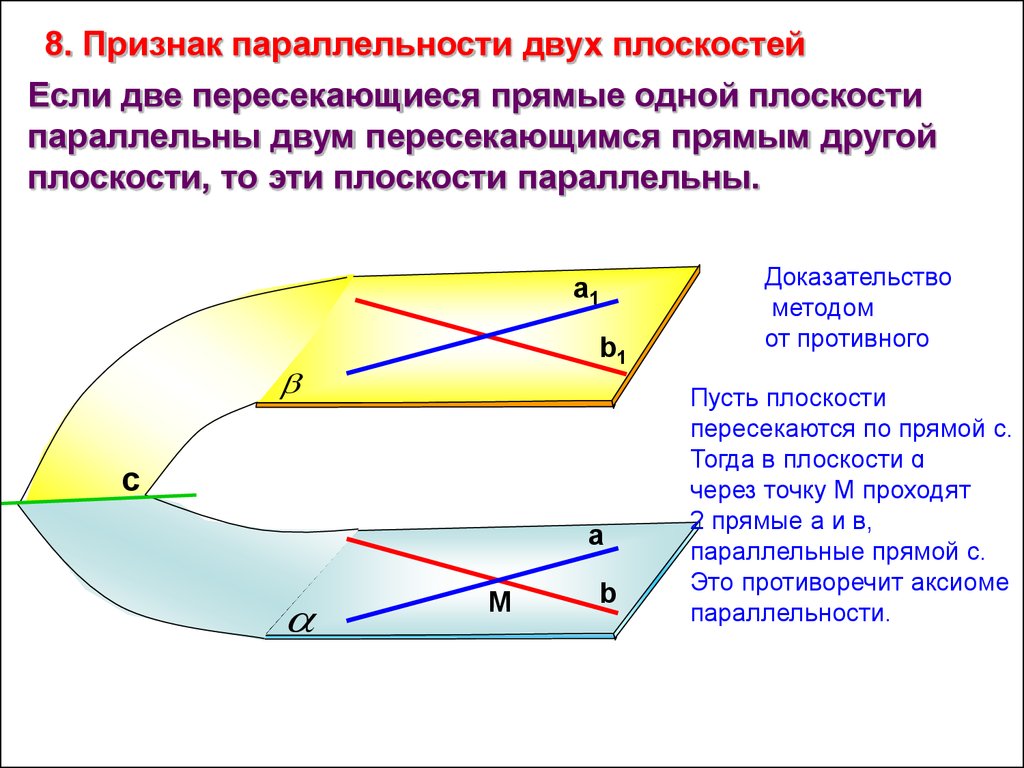
8. Признак параллельности двух плоскостей
Если две пересекающиеся прямые одной плоскости
параллельны двум пересекающимся прямым другой
плоскости, то эти плоскости параллельны.
а1
b1
с
а
M
b
Доказательство
методом
от противного
Пусть плоскости
пересекаются по прямой с.
Тогда в плоскости ɑ
через точку М проходят
2 прямые а и в,
параллельные прямой с.
Это противоречит аксиоме
параллельности.

6.

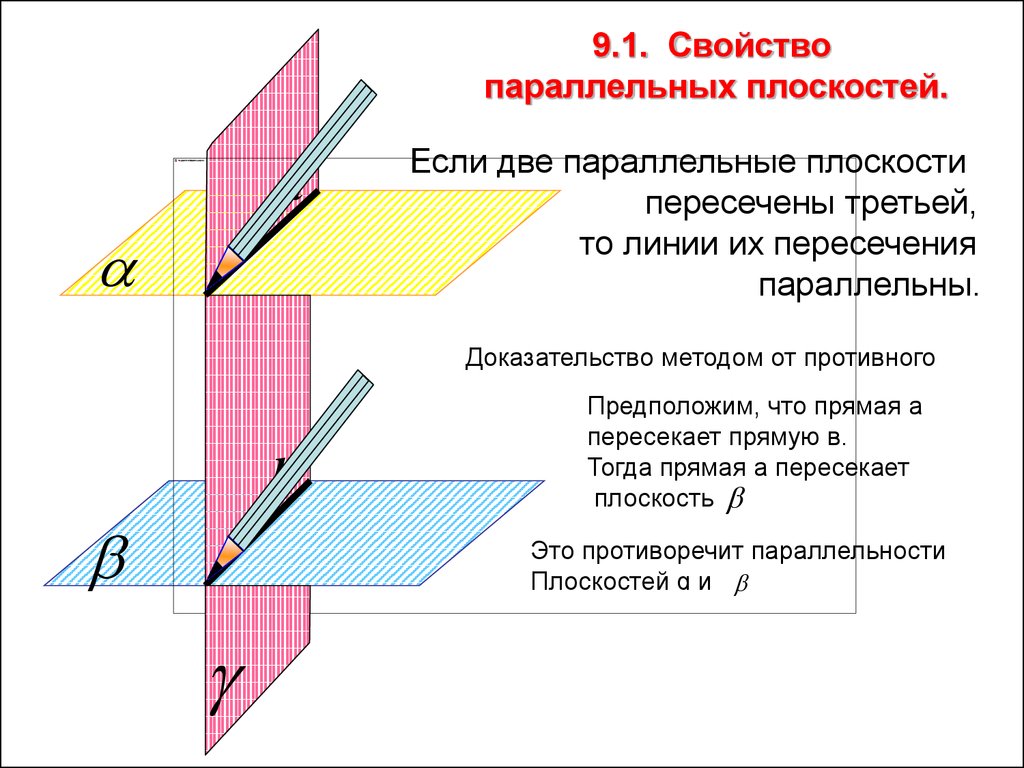
9.1. Свойство
параллельных плоскостей.
а
Если две параллельные плоскости
пересечены третьей,
то линии их пересечения
параллельны.
Доказательство методом от противного
b
Предположим, что прямая а
пересекает прямую в.
Тогда прямая а пересекает
плоскость
Это противоречит параллельности
Плоскостей ɑ и

7.

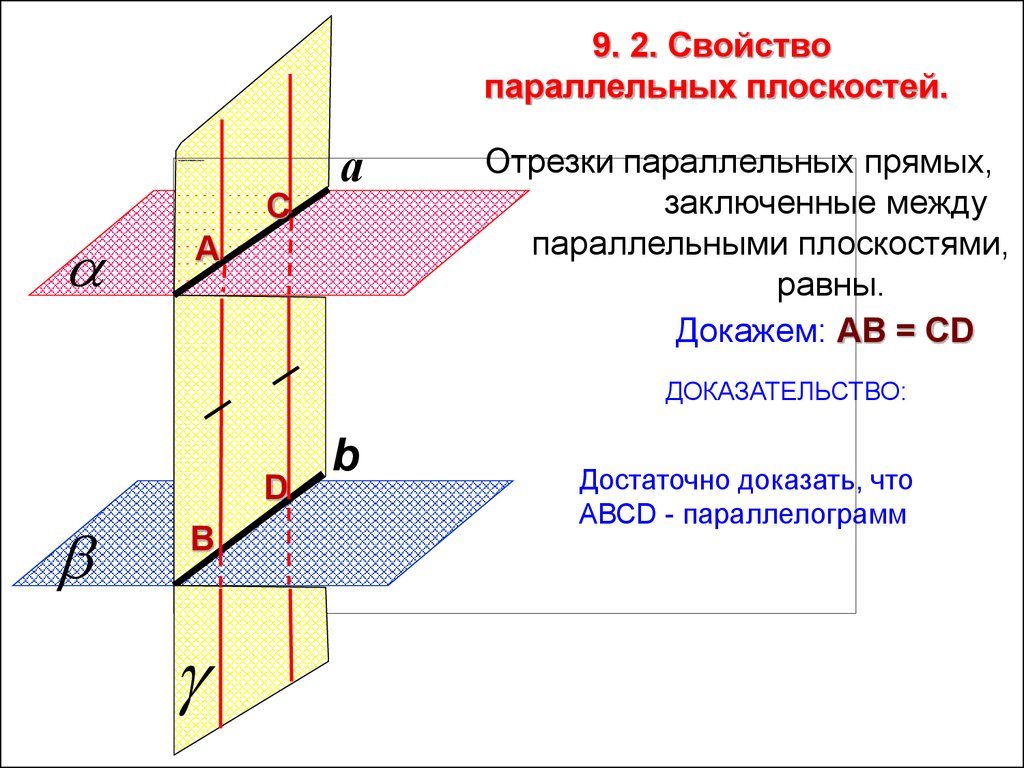
9. 2. Свойство
параллельных плоскостей.
С
а
А
Отрезки параллельных прямых,
заключенные между
параллельными плоскостями,
равны.
Докажем: АВ = СD
ДОКАЗАТЕЛЬСТВО:
D
В
b
Достаточно доказать, что
АВСD - параллелограмм