Похожие презентации:
Второе начало термодинамики. Энтропия
1.
Второе начало термодинамикиЭнтропия
dS
Q
T
2
S 2 S1
1
Q
Для обратимых
(квазистатических,
равновесных) процессов
T
Важнейшее свойство энтропии:
Энтропия замкнутой (теплоизолированной, внешние силы не
совершают работу) макросистемы, не уменьшается – она либо
возрастает, либо остаётся постоянной.
В замкнутых системах:
S 0
Ещё одна формулировка 2-го
начала
В случае обратимых процессов энтропия
замкнутой макросистемы не меняется
В случае необратимых процессов энтропия
замкнутой макросистемы возрастает
S 0
S 0
2.
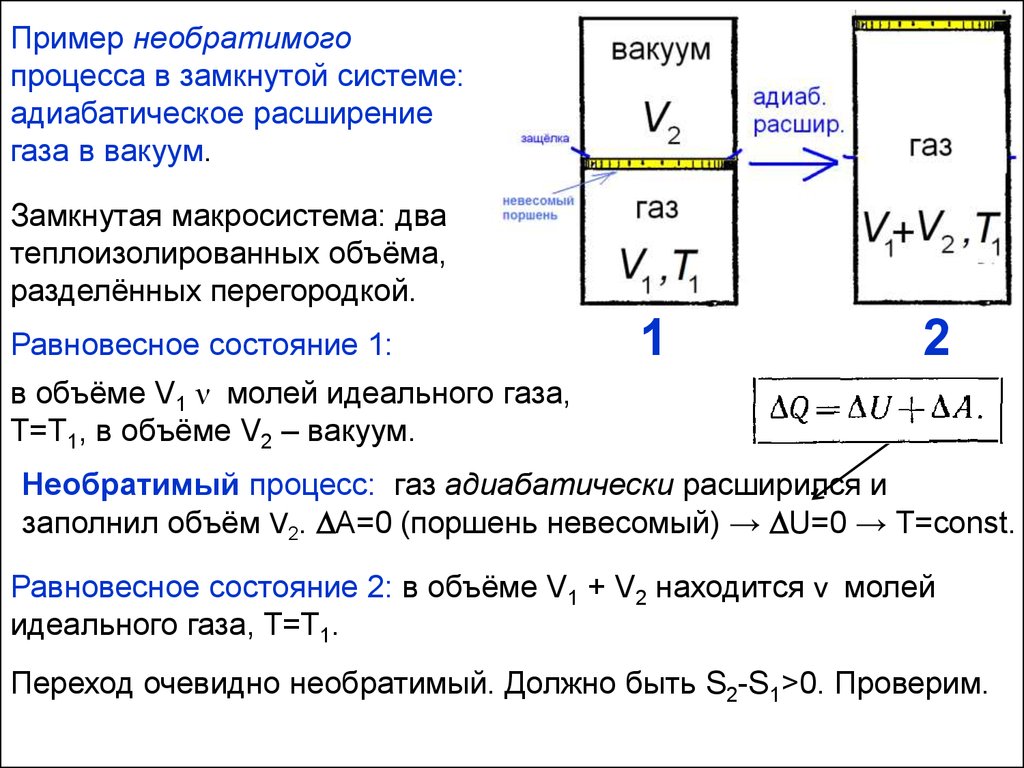
Пример необратимогопроцесса в замкнутой системе:
адиабатическое расширение
газа в вакуум.
Замкнутая макросистема: два
теплоизолированных объёма,
разделённых перегородкой.
Равновесное состояние 1:
1
2
в объёме V1 ν молей идеального газа,
T=T1, в объёме V2 – вакуум.
Необратимый процесс: газ адиабатически расширился и
заполнил объём V2. A=0 (поршень невесомый) → U=0 → Т=const.
Равновесное состояние 2: в объёме V1 + V2 находится ν молей
идеального газа, T=T1.
Переход очевидно необратимый. Должно быть S2-S1>0. Проверим.
3.
2S 2 S1
1
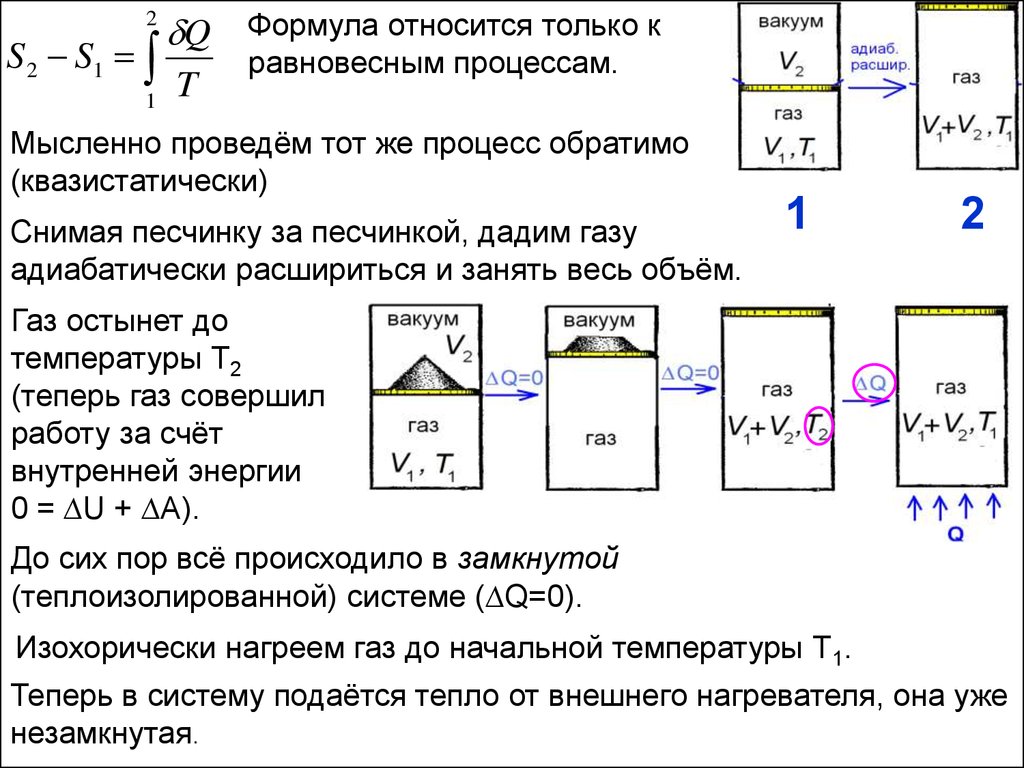
Q Формула относится только к
T
равновесным процессам.
Мысленно проведём тот же процесс обратимо
(квазистатически)
Снимая песчинку за песчинкой, дадим газу
адиабатически расшириться и занять весь объём.
1
2
Газ остынет до
температуры Т2
(теперь газ совершил
работу за счёт
внутренней энергии
0 = ∆U + ∆A).
До сих пор всё происходило в замкнутой
(теплоизолированной) системе (∆Q=0).
Изохорически нагреем газ до начальной температуры Т1.
Теперь в систему подаётся тепло от внешнего нагревателя, она уже
незамкнутая.
4.
2S 2 S1
1
Q
T
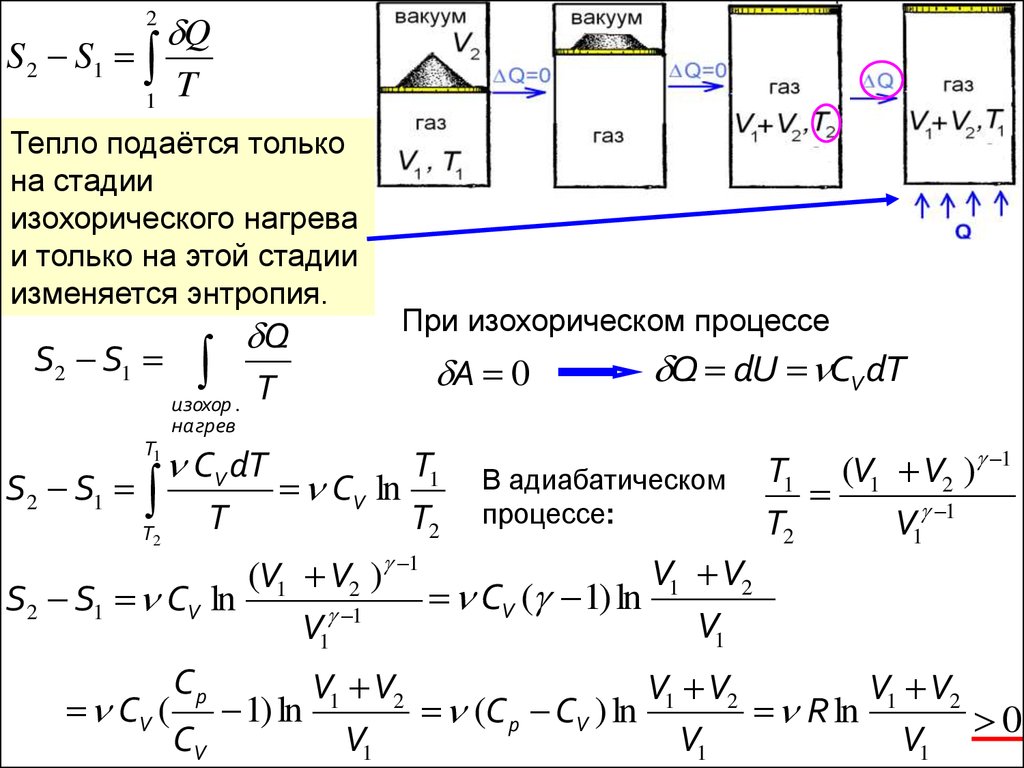
Тепло подаётся только
на стадии
изохорического нагрева
и только на этой стадии
изменяется энтропия.
S2 S1
изохор .
нагрев
T1
S2 S1
T2
Q
T
CV dT
T
При изохорическом процессе
A 0
T1
CV ln
T2
Q dU CV dT
В адиабатическом
процессе:
T1 (V1 V2 ) 1
T2
V1 1
V1 V2
(V1 V2 ) 1
CV ( 1) ln
S2 S1 CV ln
1
V1
V1
Cp
V1 V2
V1 V2
V1 V2
CV ( 1) ln
(C p CV ) ln
R ln
0
V1
V1
CV
V1
5.
Расширение газа в замкнутой системе приводит к росту энтропии.Согласно второму началу (в замкнутых
системах S 0 ), расширение газа в
замкнутой системе – необратимый
процесс.
1
2
Самопроизвольно он может протекать лишь в одну сторону.
Обратный процесс (самопроизвольное сжатие) запрещён вторым
началом (поскольку энтропия при этом снижается).
Таким образом, анализ изменения энтропии указывает, какие
неравновесные процессы в замкнутой системе возможны
(протекают самопроизвольно), а какие нет.
6.
Статистический смысл энтропииВ замкнутых системах:
S 0
Самопроизвольные процессы протекают в направлении роста энтропии.
С другой стороны, макросистема представляет собой ансамбль огромного
числа частиц, поведение которых подчиняется статистическим законам.
Самопроизвольно макросистема переходит в то состояние, которое
наиболее вероятно.
Например, если мысленно разделить объём V,
заполненный газом, пополам, то крайне маловероятно, что
все молекулы соберутся в одной из его частей, а другая
окажется пустой.
И наоборот, если такая ситуация искусственно
создана, когда мы убираем перегородку, газ
немедленно заполняет весь объём, т.е. система
самопроизвольно переходит в более вероятное
состояние (и в то же время увеличивается энтропия).
7.
Статистический смысл энтропииТермодинамическая вероятность (статистический вес).
Макросостояние характеризуется термодинамическими
параметрами p, V, T.
Но, макросистема состоит из громадного числа молекул (или
атомов).
Молекулы газа могут иметь разные импульсы и координаты.
Состояние с определёнными значениями всех координат и
импульсов всех молекул системы называется микросостоянием.
Любому макросостоянию соответствует громадное число
микросостояний.
Чем большим числом способов (микросостояний) может быть
осуществлено данное макросостояние, тем оно более вероятно.
Термодинамическая вероятность данного макросостояния W
равна числу способов (числу микросостояний), которыми может
быть осуществлено данное макросостояние.
8.
Статистический смысл энтропииТермодинамическая вероятность (статистический вес).
Термодинамическая вероятность W – огромное число (это не
математическая вероятность, которая не превосходит 1).
Термодинамическую вероятность называют также статистическим
весом.
Связь термодинамической вероятности состояний идеального
газа с его объёмом.
Число способов, которым можно разместить одну молекулу в
объёме V пропорционально V.
Число способов, которым можно разместить в объёме V N молекул
пропорционально
Термодинамическая вероятность состояния идеального газа:
W~ VN.
9.
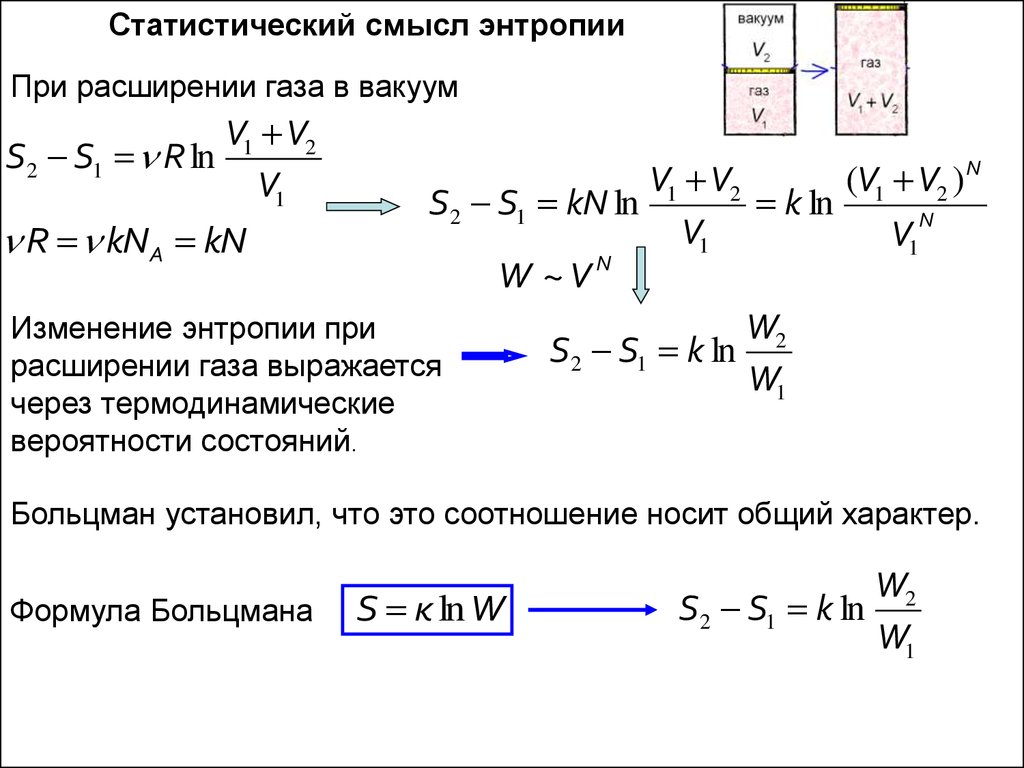
Статистический смысл энтропииПри расширении газа в вакуум
V1 V2
S2 S1 R ln
V1
V1 V2
(V1 V2 ) N
S2 S1 kN ln
k ln
N
V
V1
R kNA kN
1
W ~VN
W2
Изменение энтропии при
S2 S1 k ln
расширении газа выражается
W1
через термодинамические
вероятности состояний.
Больцман установил, что это соотношение носит общий характер.
Формула Больцмана
S к ln W
W2
S2 S1 k ln
W1
10.
Статистический смысл энтропииS к ln W
W2
S2 S1 S k ln
0
W1
В замкнутой системе самопроизвольные процессы совершаются в
направлении более вероятных состояний.
Более вероятные состояния – менее
упорядоченные, более однородные.
Например, самопроизвольные процессы идут в
направлении выравнивания давления и
температуры.
Гипотеза о «тепловой смерти вселенной».
Принцип возрастания энтропии не относится к открытым системам,
например, живым.
11.
Третье начало термодинамикиПри Т = 0 К
система обладает наименьшей возможной энергией,
её внутренняя энергия распределена между составляющими ее
частицами единственным способом, а именно
все электроны в атомах находятся при этом в наинизших
энергетических состояниях,
а атомы располагаются в пространстве определенным образом (в
узлах кристаллической решетки твердого тела).
Благодаря полной упорядоченности этого единственного состояния
его термодинамическая вероятность W = 1.
Нернст 1906, Планк 1911
При абсолютном нуле энтропия тела обращается в нуль.
Возможность определять абсолютное значения энтропии.
12.
Основное уравнение термодинамики для обратимых(квазистатических) процессов (объединяет 1 и 2 начала).
dS
Q
T
Q TdS
Q dU pdV
ТdS dU pdV
Для обратимых процессов
Энтропия идеального газа
Найдём S2 – S1 для двух состояний ν молей идеального газа: V1, T1
и V 2 , T2
dU СV dT ; PV RT
dU p
dT
dV
dS
dV CV
R
T
T
T
V
13.
Энтропия идеального газаdU p
dT
dV
dS
dV CV
R
T
T
T
V
V2
dT
dV ( C ln T2 R ln V2 )
S 2 S1 dS CV
V
R
T1
V1
T
V
1
T1
V1
2
T2
Энтропия возрастает при увеличении V и T (больше беспорядка).
При Т2=Т1
V2
S 2 S1 R ln
V1
Адиабатическое
расширение в вакуум
14.
ДО СИХ Тепловая машина, цикл КарноВторое начало: в замкнутой системе энтропия не может убывать.
В замкнутой системе мы хотим отнять тепло Q1 от нагретого тела
и за счёт этого тепла совершить работу.
Q1
Энтропия этого тела уменьшится на величину : S1
T1
Но энтропия замкнутой системы не может убывать.
Q2
S 2
T2
Q2 Q1
Таким образом этому телу должно быть передано
тепло ∆Q2 и при этом должно быть ∆S2≥ ∆S1, т.е.
T2
T1
Поэтому должно быть другое тело, энтропия
которого возрастёт настолько же или больше.
Тепло, переданное второму телу, ∆Q2 меньше, чем ∆Q1 (иначе не
получить работу).
Поскольку
Q2 Q1 , должно быть Т2<T1.
Нужно более
холодное тело.
15.
Для получения работы необходимо «рабочее тело», котороедолжно
обратимо отнять тепло Q1 от нагревателя,
обратимо отдать часть тепла Q2 холодильнику,
разность Q1 — Q2 передать поршню в виде механической работы
А.
вернуться в исходное состояние, т. е. совершить замкнутый цикл и
далее повторять его.
16.
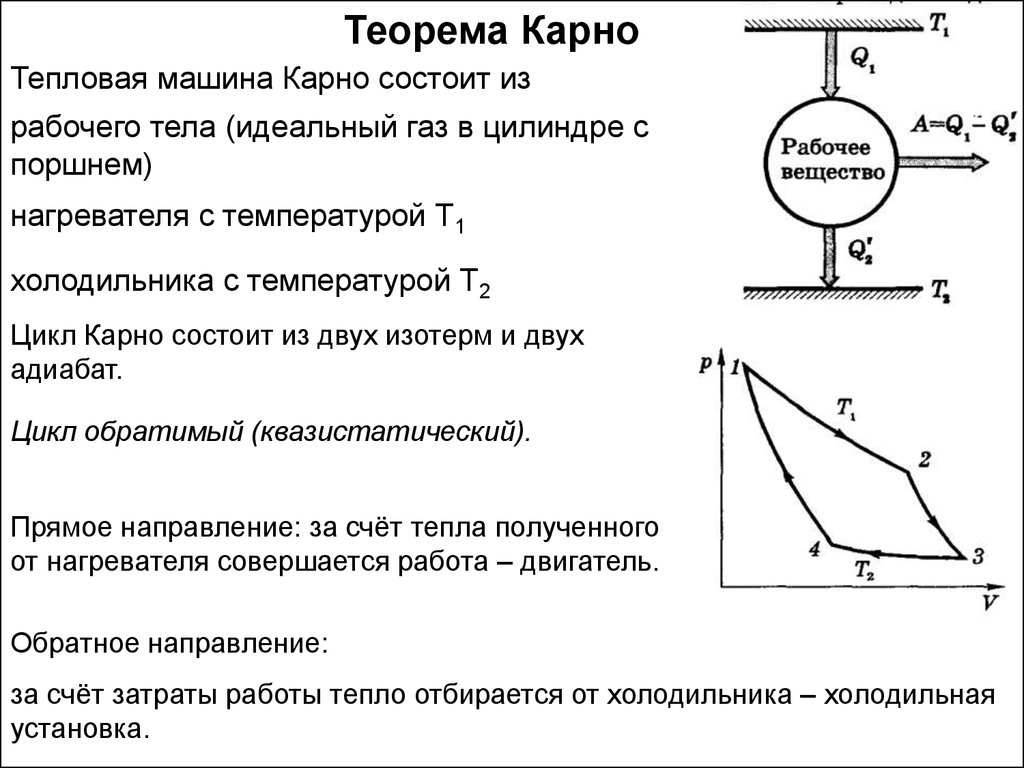
Теорема КарноТепловая машина Карно состоит из
рабочего тела (идеальный газ в цилиндре с
поршнем)
нагревателя с температурой Т1
холодильника с температурой Т2
Цикл Карно состоит из двух изотерм и двух
адиабат.
Цикл обратимый (квазистатический).
Прямое направление: за счёт тепла полученного
от нагревателя совершается работа – двигатель.
Обратное направление:
за счёт затраты работы тепло отбирается от холодильника – холодильная
установка.
17.
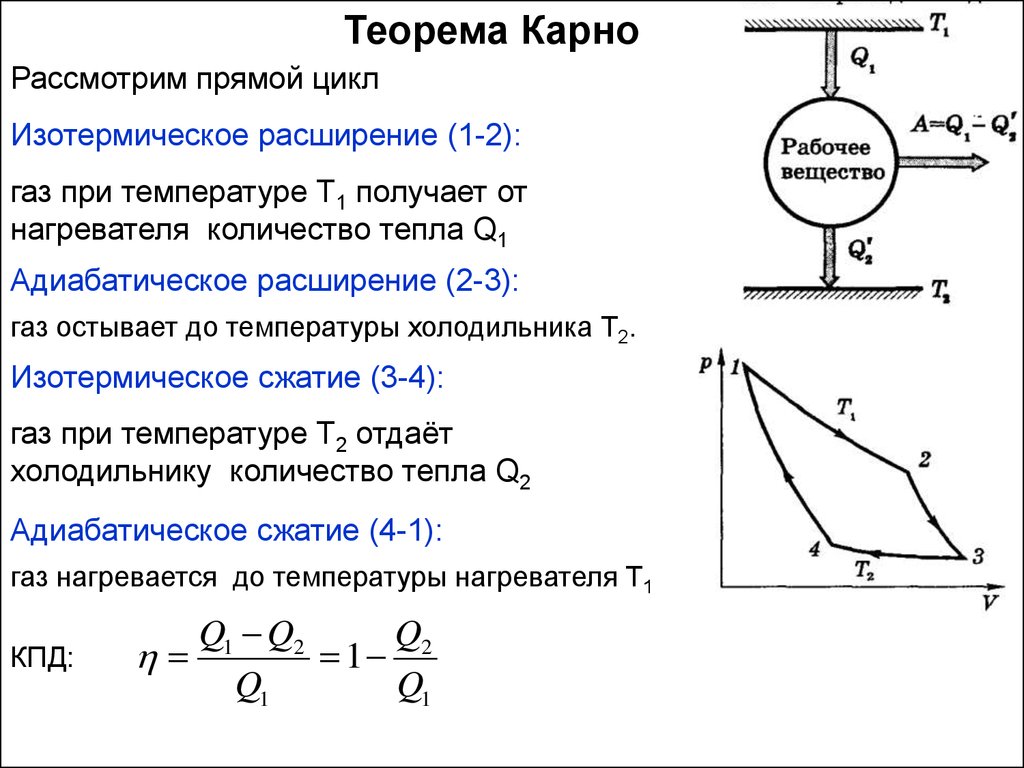
Теорема КарноРассмотрим прямой цикл
Изотермическое расширение (1-2):
газ при температуре Т1 получает от
нагревателя количество тепла Q1
Адиабатическое расширение (2-3):
газ остывает до температуры холодильника Т2.
Изотермическое сжатие (3-4):
газ при температуре Т2 отдаёт
холодильнику количество тепла Q2
Адиабатическое сжатие (4-1):
газ нагревается до температуры нагревателя Т1
КПД:
Q1 Q2
Q2
1
Q1
Q1
18.
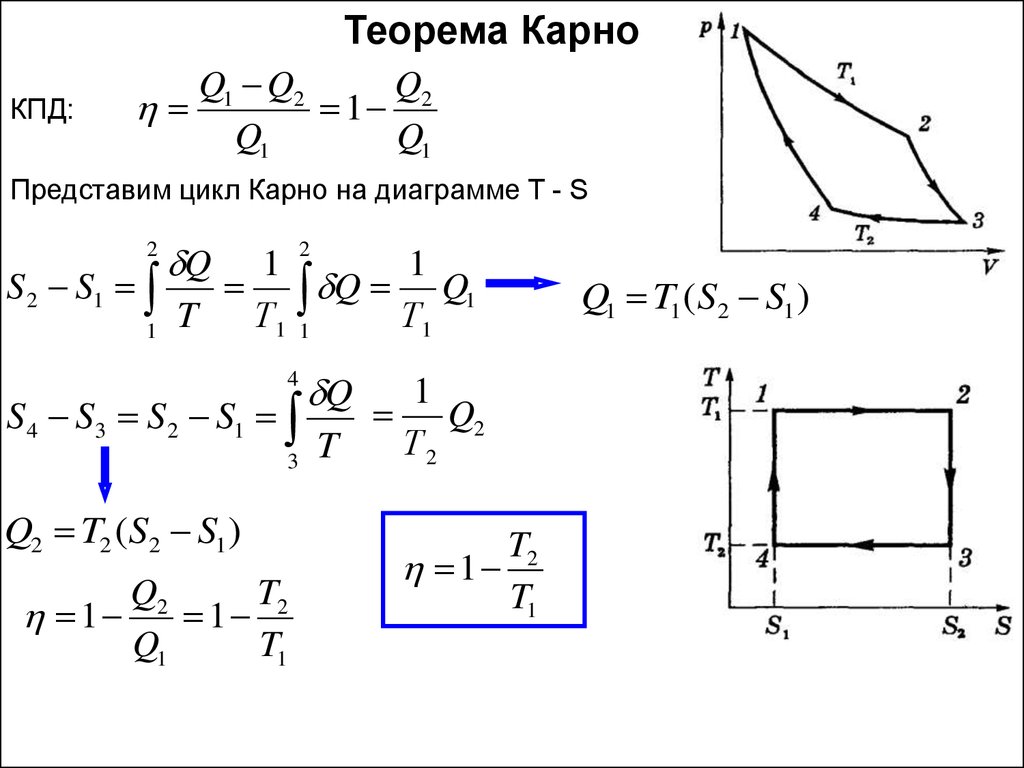
Теорема КарноКПД:
Q1 Q2
Q2
1
Q1
Q1
Представим цикл Карно на диаграмме T - S
2
S 2 S1
1
Q
2
1
1
Q Q1
T
Т1 1
Т1
4
S4 S3 S2 S1
3
Q2 T2 (S2 S1 )
Q2
T2
1
1
Q1
T1
Q
1
Q2
Т2
T
T2
1
T1
Q1 T1 (S2 S1 )
19.
Теорема КарноT2
1
T1
При выводе не делалось никаких предположений о конкретном
устройстве двигателя или вида рабочего вещества.
Теорема Карно:
КПД обратимых двигателей, работающих по циклу Карно,
зависит только от температур Т1 и Т2 – нагревателя и
холодильника, но не зависит ни от устройства двигателя, ни от
вида рабочего вещества.
Можно показать
КПД любой необратимой (реальной) тепловой
машины, работающей с тем же нагревателем и
холодильником, всегда ниже, чем у машины
работающей по обратимому циклу Карно:
T2
1
T1
20.
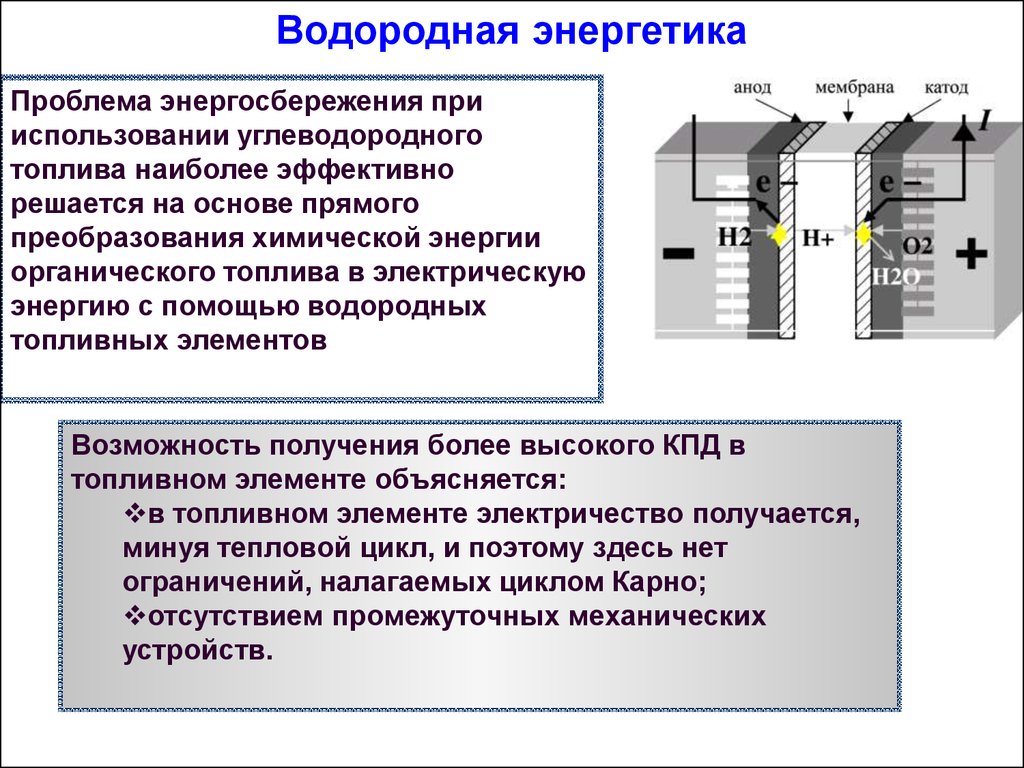
Водородная энергетикаПроблема энергосбережения при
использовании углеводородного
топлива наиболее эффективно
решается на основе прямого
преобразования химической энергии
органического топлива в электрическую
энергию с помощью водородных
топливных элементов
Возможность получения более высокого КПД в
топливном элементе объясняется:
в топливном элементе электричество получается,
минуя тепловой цикл, и поэтому здесь нет
ограничений, налагаемых циклом Карно;
отсутствием промежуточных механических
устройств.
21.
Разработка японской фирмы Casio:источник питания для ноутбука
Первичный источник энергии:
смесь метанола с водой.
Из метанольно-водяной смеси
получается водород.
Водород подаётся на твёрдополимерный топливный элемент.
Не требует источника
электричества для зарядки.
Работает в 4 раза дольше в том же
объёме, что и ионно-литиевая
батарея (включая топливный
картридж).
Напряжение 13.9 В, мощность 19.4 Вт.
Размеры: 65*18*19 мм3 = 22 мл.
Плотность энергии: 882 Вт/л - рекордная!
7
22.
ООО инновационнаякомпания «МЕВОДЕНА»,
резидент СКОЛКОВО (к. 103)
Эксперимент в Российском ядерном
центре (Саров):
отделение трития от гелия с помощью
сверхпроницаемых мембран
13
23.
Эксперимент сосверхпроницаемой
мембраной в
Национальном Институте
Термоядерных
Исследований Японии
Large Helical Device
Мембранная панель разработанная в ГУТ
обращена непосредственно в плазму.
14















 Физика
Физика








