Похожие презентации:
Идеальная (обратимая) тепловая машина, цикл Карно
1.
Идеальная (обратимая) тепловая машина, цикл КарноДля получения работы необходимо «рабочее тело», которое
должно
обратимо отнять тепло DQ1 от нагревателя,
обратимо отдать часть тепла DQ2 холодильнику,
разность DQ1 — DQ2 передать поршню в виде механической работы
DА.
вернуться в исходное состояние, т. е. совершить замкнутый цикл и
далее повторять его.
2.
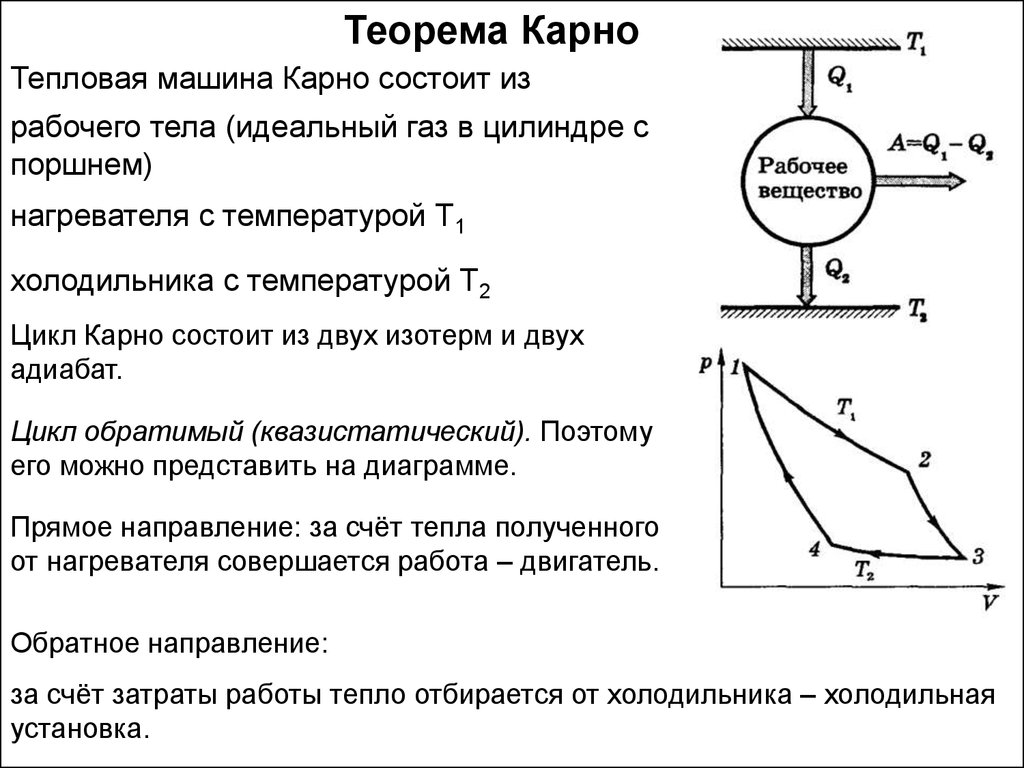
Теорема КарноТепловая машина Карно состоит из
рабочего тела (идеальный газ в цилиндре с
поршнем)
нагревателя с температурой Т1
холодильника с температурой Т2
Цикл Карно состоит из двух изотерм и двух
адиабат.
Цикл обратимый (квазистатический). Поэтому
его можно представить на диаграмме.
Прямое направление: за счёт тепла полученного
от нагревателя совершается работа – двигатель.
Обратное направление:
за счёт затраты работы тепло отбирается от холодильника – холодильная
установка.
3.
Теорема КарноРассмотрим прямой цикл
Изотермическое расширение (1-2):
газ при температуре Т1 получает от
нагревателя количество тепла Q1
Адиабатическое расширение (2-3):
газ остывает до температуры холодильника Т2.
Изотермическое сжатие (3-4):
газ при температуре Т2 отдаёт
холодильнику количество тепла Q2
Адиабатическое сжатие (4-1):
газ нагревается до температуры нагревателя Т1
КПД:
Q1 Q2
Q2
1
Q1
Q1
4.
Теорема КарноКПД:
Q1 Q2
Q2
1
Q1
Q1
Представим цикл Карно на диаграмме T - S
2
S 2 S1
1
Q
2
1
1
Q Q1
T
Т1 1
Т1
4
S4 S3 S2 S1
3
Q2 T2 (S2 S1 )
Q2
T2
1
1
Q1
T1
Q
1
Q2
Т2
T
T2
1
T1
Q1 T1 (S2 S1 )
5.
Теорема КарноT2
1
T1
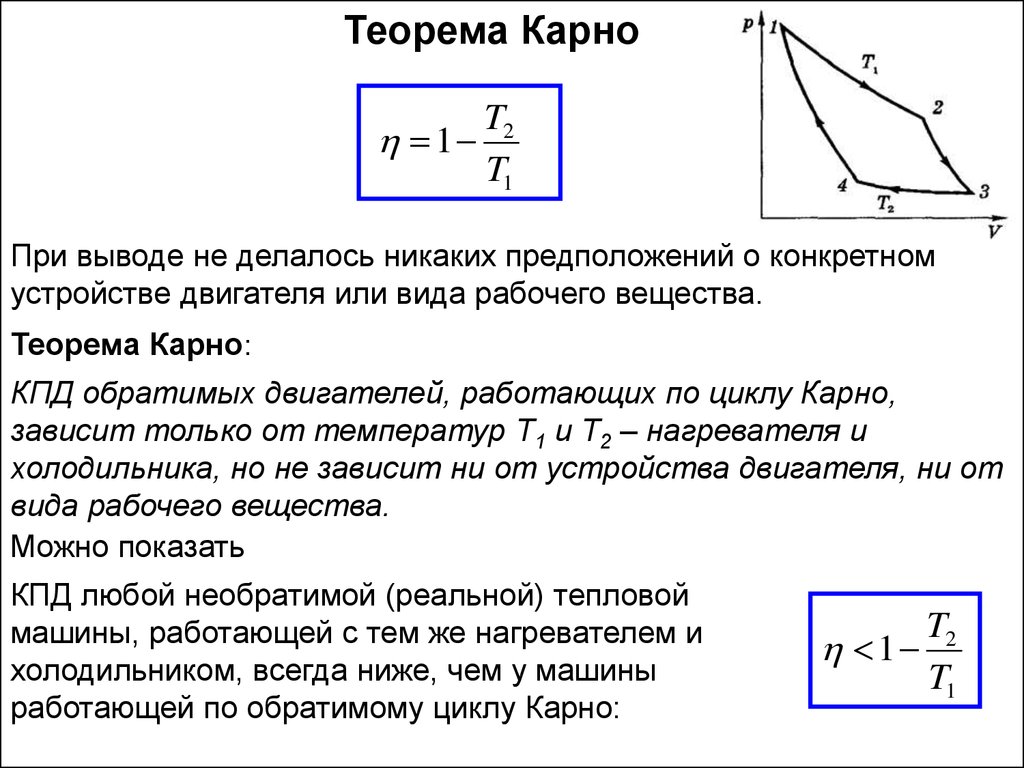
При выводе не делалось никаких предположений о конкретном
устройстве двигателя или вида рабочего вещества.
Теорема Карно:
КПД обратимых двигателей, работающих по циклу Карно,
зависит только от температур Т1 и Т2 – нагревателя и
холодильника, но не зависит ни от устройства двигателя, ни от
вида рабочего вещества.
Можно показать
КПД любой необратимой (реальной) тепловой
машины, работающей с тем же нагревателем и
холодильником, всегда ниже, чем у машины
работающей по обратимому циклу Карно:
T2
1
T1
6.
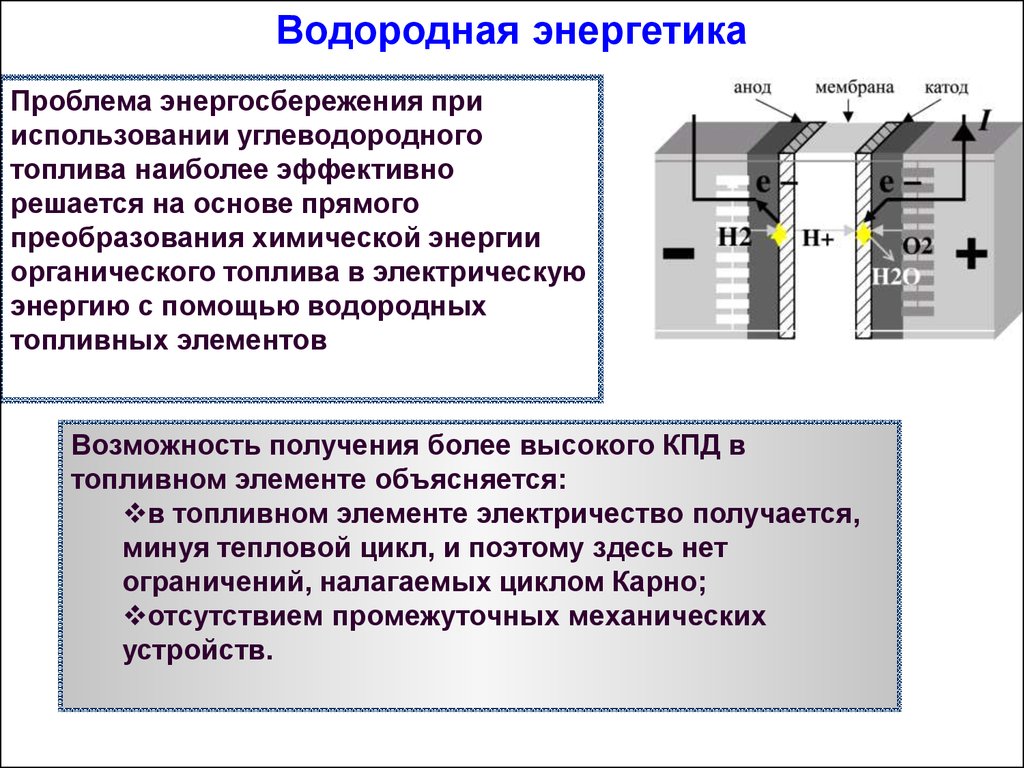
Водородная энергетикаПроблема энергосбережения при
использовании углеводородного
топлива наиболее эффективно
решается на основе прямого
преобразования химической энергии
органического топлива в электрическую
энергию с помощью водородных
топливных элементов
Возможность получения более высокого КПД в
топливном элементе объясняется:
в топливном элементе электричество получается,
минуя тепловой цикл, и поэтому здесь нет
ограничений, налагаемых циклом Карно;
отсутствием промежуточных механических
устройств.
7.
Разработка японской фирмы Casio:источник питания для ноутбука
Первичный источник энергии:
смесь метанола с водой.
Из метанольно-водяной смеси
получается водород.
Водород подаётся на твёрдополимерный топливный элемент.
Не требует источника
электричества для зарядки.
Работает в 4 раза дольше в том же
объёме, что и ионно-литиевая
батарея (включая топливный
картридж).
Напряжение 13.9 В, мощность 19.4 Вт.
Размеры: 65*18*19 мм3 = 22 мл.
Плотность энергии: 882 Вт/л - рекордная!
7
8.
ООО инновационнаякомпания «МЕВОДЕНА»,
резидент СКОЛКОВО (к. 103)
Эксперимент в Российском ядерном
центре (Саров):
отделение трития от гелия с помощью
сверхпроницаемых мембран
13
9.
Эксперимент сосверхпроницаемой
мембраной в
Национальном Институте
Термоядерных
Исследований Японии
Large Helical Device
Мембранная панель разработанная в ГУТ
обращена непосредственно в плазму.
14
10.
ОПТИЧЕСКИЕ ЯВЛЕНИЯ11.
Историческая дискуссия о природе света:Свет - это поток частиц или это волны (в мировом эфире)?
Трёхвековая дискуссия
Корпускулярно-волновой дуализм (Луи де Бройль) : свет обладает
одновременно волновыми и корпускулярными свойствами .
В некоторых проявлениях свет ведёт себя как волна
(электромагнитная): интерференция, дифракция.
В других – как поток частиц (фотонов): фотоэффект, эффект
Комптона
Согласно современным представлениям не только фотоны, но и
электроны и любые другие частицы материи наряду с
корпускулярными обладают также волновыми свойствами.
12.
ЯВЛЕНИЯ ВОЛНОВОЙОПТИКИ
13.
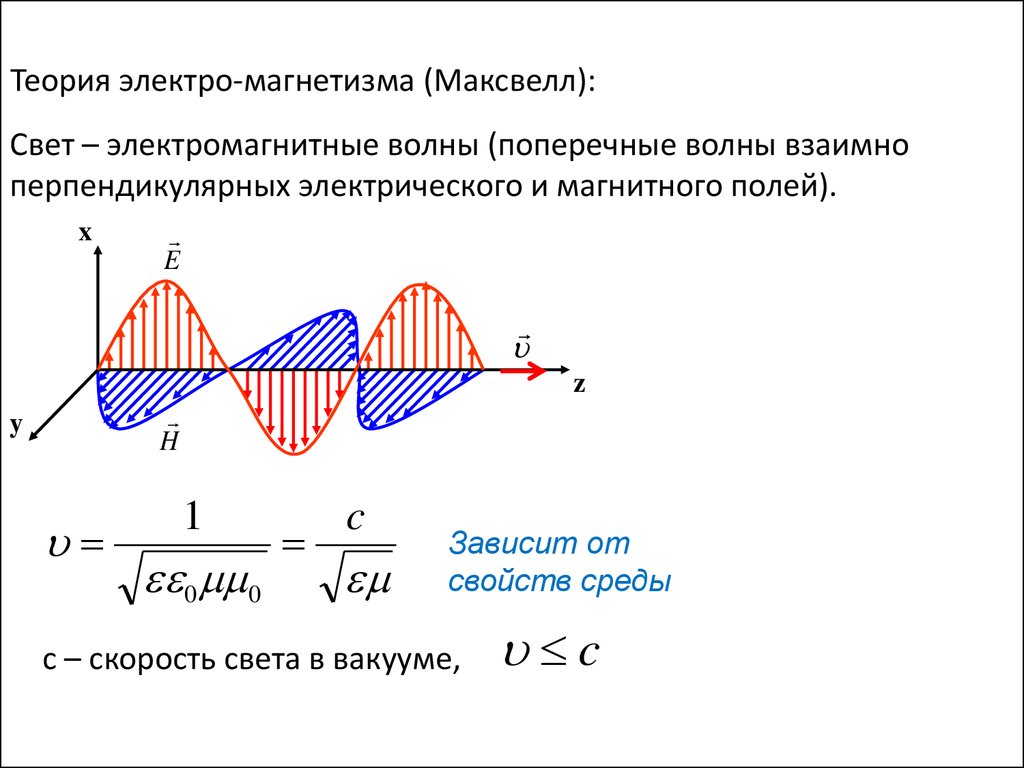
Теория электро-магнетизма (Максвелл):Свет – электромагнитные волны (поперечные волны взаимно
перпендикулярных электрического и магнитного полей).
x
E
z
H
y
1
0 0
c
Зависит от
свойств среды
с – скорость света в вакууме,
c
14.
ШКАЛА ЭМВ1мкм 10 м 10 А
6
9
1нм 10 м 10 A
10
10
м 1A
4
15.
16.
17.
Суперпозиция 2-х волн одинаковой частоты и одинаковогонаправления колебаний, распространяющихся в однородной среде
r1
Р
S1
r2
От источника S1 в точку Р приходят колебания :
1 a1 cos( t kr1 1 ) a1 cos( t 1 )
От источника S2 в точку Р приходят колебания :
2 a2 cos( t kr2 2 ) a2 cos( t 2 )
S2
Результирующее колебание в точке Р:
Сложение
однонаправленных
колебаний одной частоты
1 2 a cos( t ) , где tg a1 sin 1 a2 sin 2
a1 cos 1 a2 cos 2
a 2 a12 a22 2a1a2 cos( 1 2 )
I1 , I 2 , I - Интенсивности колебаний, приходящих в точку Р от 1-го и 2-го
источника, и результирующая интенсивность колебаний
соответственно.
I1 a12
I2
a22
I
a2
I I1 I 2 2 I1I 2 cos( 1 2 )
18.
I I1 I 2 2 I1I 2 cos( 1 2 )Интерференционный
член
Волны одинаковой частоты и одинакового направления
колебаний называются когерентными, если
1 2 const.
разность фаз
(начальных) колебаний
постоянна во времени
Некогерентные волны: разность фаз непрерывно меняется
cos( 1 2 ) 0
I I1 I 2
Монотонное распределение
интенсивности
Когерентные волны, 1 2 const. Пусть I1 I 2
1 2 2m , I 4I 1;
1 2 (2m 1) , I 0
Чередование максимумов и минимумов интенсивности
Интерференция, результат суперпозиции когерентных волн
19.
Проблема когерентности в волновой оптике:Волны естественного света не когерентны!
Причина: световые волны излучаются атомами
1) излучение света атомом носит случайный характер;
2) длительность спонтанного излучения одного атома порядка
10 наносекунд;
3) одновременно свет излучается большим числом атомов;
4) излучение света не монохроматическое.
20.
ПРОСТРАНСТВЕННАЯ И ВРЕМЕННАЯ КОГЕРЕНТНОСТЬ1 a1 cos( t kr1 1 )
2 a2 cos( t kr2 2 )
Основная проблема: в естественной световой волне
образом меняется во времени и пространстве.
беспорядочным
Временная когерентность: разность фаз двух колебаний в
данной точке пространства остаётся неизменной во времени:
( t kr2 2 ) ( t kr1 1 ) const (t )
2 1 const (t )
Время когерентности t: время за которое случайное изменение фазы (α)
достигает значения ≈ .
Поскольку световые волны испускаются атомами, t - время спонтанного
излучения атома
t ≈10-8 сек
21.
ПРОСТРАНСТВЕННАЯ И ВРЕМЕННАЯ КОГЕРЕНТНОСТЬ1 a1 cos( t kr1 1 )
2 a2 cos( t kr2 2 )
Основная проблема: в естественной световой волне
образом меняется во времени и пространстве.
беспорядочным
Пространственная когерентность: определяется расстоянием l вдоль волновой
поверхности, на котором случайное изменение фазы достигает значения ≈ .
Разные участки нагретых тел излучают независимо. Вблизи поверхности такого
источника света l ≈ λ.
Волны естественного света (в отличие от волн испускаемых
лазерами!) не обладают ни временной, ни пространственной
когерентностью.
Решение для естественного света:
Использование одного
монохроматического источника для
формирования 2-х когерентных волн.
1 2
22.
Связь оптической разности хода лучей и разности фаз колебанийT
0 Tc
Длина волны в среде.
Длина волны в вакууме
1
0 c n
1 a1 cos( t kr1 1 )
0
,
0
n
1
фаза в точке Р
2
фаза в точке Р
2 a2 cos( t kr2 2 )
1 2 одна разделённая волна
1 2
2
0
D
оптическая разность хода
23.
Оптическая разность хода, дающая максимумы и минимумы интенсивностиI I1 I 2 2 I1I 2 cos( 1 2 )
Интерференционный
член
Условие максимума
1 2 2m
1 2
2
0
D
D m 0 2 m
0
при I1 = I2
2
I 4I 1
Условие минимума
1 2 (2m 1)
1 2
2
0
D (2 m 1)
D
Не когерентные источники:
0
2
при I1 = I2
I 0
cos( 1 2 ) 0 I I1 I 2
24.
25.
Интерференция от двухкогерентных источников света
Когерентные
источники - нити
Когерентные
цилиндрические
волны
поле
интерференции
Найдём положение максимумов на экране
d
r l x
2
2
d
r l x
2
2
2
1
2
2
2
r22 r12 2 xd
2
(r2 r1 )(r2 r1 ) 2 xd
(обычно d<<l )
r2 r1
щель
D
n
r2 r1 2l
l
D
x
D
2l 2 xd
nd
Положение n
максимума
D max 2m 0
2
l
l
m 0,1,2,...
xmax m 0 m
nd
d
Dxmax
l
l
0
nd
d
26.
Распределение интенсивности света на экране.Положение максимумов
интенсивности
xmax
l
l
m 0 m
nd
d
Расстояние между
максимумами
Dxmax
m 0,1,2,...
Условия наилучшего наблюдения…
Естественный свет…
Способ измерения длины волны света
l
l
0
nd
d
27.
СОЛНЕЧНЫЙ СВЕТСхема опыта Юнга
28.
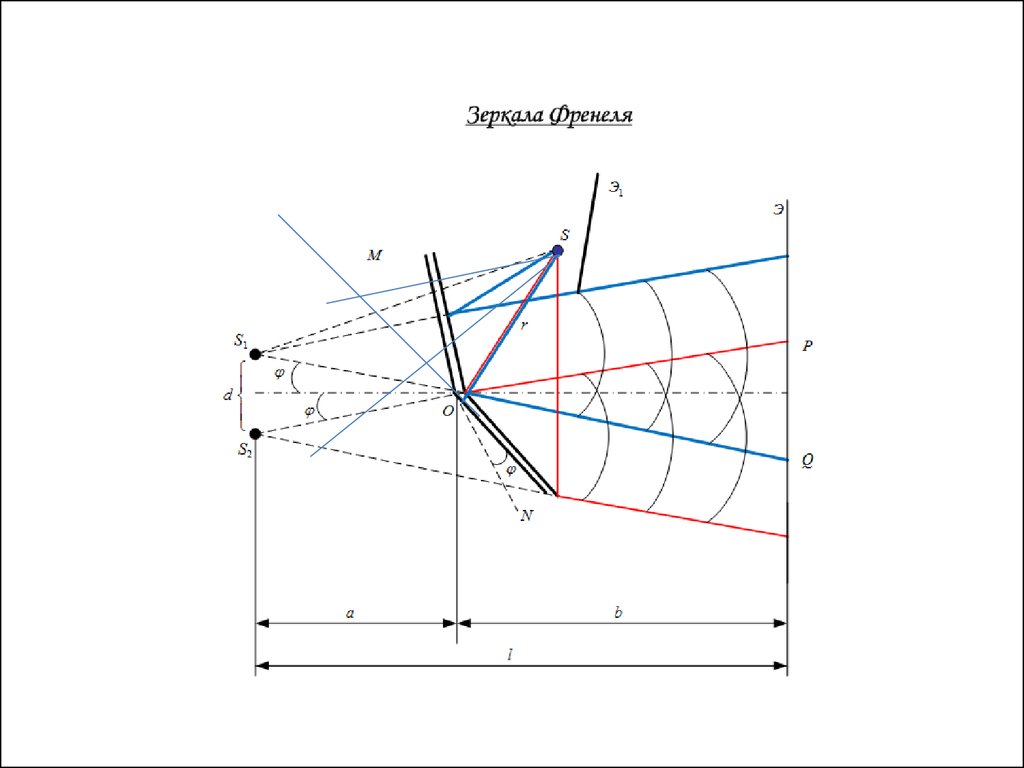
Зеркала ФренеляДва плоских зеркала под
малым углом ϕ.
Два мнимых изображения
(S1 и S2) протяжённого
источника S, закрытого
экраном Э1 – когерентные
источники световых волн.
Dxmax
l
l
0
nd
d
Dxmax
Самостоятельно, Савельев т.3.
r b
0
2r
29.
Бипризма ФренеляДве прозрачные призмы с
малым углом преломления (β)
с общим основанием .
Линейный источник света
(наклённая нить, светящаяся щель)
Преломлённвые каждой призмой
лучи дают два мнимых
изображения источника (S1 и S2) когерентные источники световых
волн.
l
l
Dxmax
0
nd
d
Самостоятельно, Савельев т.3.
Dxmax
r b
0
2r
30.
Самостоятельно, Савельев т.3.Интерференция света отражённого
от тонких пластинок (плёнок)
Полосы равной толщины
Интерференция на клине
Кольца Ньютона
31.
32.
1629-16951788-1827
Дифракция – явление огибания волнами препятствий,
проникновения колебаний в область геометрической тени и
другие подобные отступления от геометрической оптики.
33.
Принцип ГюйгенсаКаждую точку волнового фронта в момент времени t
можно рассматривать как точечный источник
вторичных волн.
Огибающая вторичных волн, испущенных за время ∆ t,
дает положение фронта волны в момент времени t + ∆ t .
Принцип Гюйгенса - Френеля
t+ t
Принцип Гюйгенса + представление об
интерференции вторичных волн
34.
Принцип Гюйгенса – ФренеляКаждый элемент волновой поверхности площадью dS служит
источником вторичной сферической волны, от которой в некоторую
точку Р приходят колебания:
d K ( )
Волновая поверхность
(все точки колеблются в
одинаковых фазах)
r Р
dS
t 0
a0
- фаза колебаний в точках
волновой поверхности S
- амплитуда колебаний в том
месте, где находится dS .
K ( )
n
K (
S
a0 dS
cos( t kr 0 )
r
- коэффициент, убывающий при
увеличении
) 0
2
Результирующее колебание в точке Р – суперпозиция колебаний,
приходящих от всех dS волновой поверхности S :
a0 dS
K ( )
cos( t kr 0 )dS
r
S
Принцип Гюйгенса – Френеля
в аналитической форме.
35.
Не очень понятно почему К(ϕ) убывет с ростом ϕ, если вторичная волнасферическая. У Савельева это аргументировано просто ссылкой на Френеля (см
ниже). Значит он тоже видит эту проблему (?).
Во всяком случае это противоречит
картинке:
Савельев:
36.
Принцип Гюйгенса – Френеляr Р
dS
n
Результирующее колебание в точке Р –
суперпозиция колебаний, приходящих от всех dS
волновой поверхности S :
K ( )
S
a0 dS
cos( t kr 0 )dS
r
S
Трудная вычислительная задача!
При высокой степени симметрии задача легко решается
приближённым методом зон Френеля.
37.
38.
Построение зон Френеля (инструкция).Рассмотрим точечный источник волн, находящийся в однородной,
изотропной среде.
S – точечный источник света.
P – произвольная точка пространства.
- длина волны в среде.
P
1)
S
волновая
поверхность
39.
P2)
S
SP
O
О – точка пересечения SP с волновой поверхностью
40.
3)P
Точка О – центр кольцевых зон,
построенных так, что расстояния
от краев каждой зоны до точки Р
отличаются на величину, равную
2
O
S
b 3
2
b 2
2
b
2
4)
P
O
b
S
Расстояние от внешнего
края т-ой зоны до точки Р :
bm b m
1-я зона
2-я зона
3-я зона
и т.д.
2
m 1, 2, 3,....
41.
42.
Свойства зон Френеля, прямолинейностьраспространения света
1. Колебания, приходящие в точку Р от
аналогичных точек двух соседних зон,
находятся в противофазе. Результирующие
колебания, приходящие в точку Р от соседних
зон Френеля, будут отличаться по фазе на
2. Площадь т-ой зоны Френеля
ab
DSm
a b
DSm - не зависит от т
3. Внешние радиусы зон
Френеля
Вывод ∆Sm и rm -cамостоятельно!
Савельев т. 3
ab
rm
a b
rm
a b 1m
0.5mkm
0.5 мм
m
пропорционален
m
43.
4. Принцип Гюйгенса – Френеля:С увеличением «т»
a0 dS
dA K ( )
r
ДО СИХ
Амплитуды колебаний, приходящих
в точку Р , от зон Френеля
образуют монотонно убывающую
последовательность:
A1 A2 A3 A4 ...
DSm
практически не меняется;
r bm
угол
f
медленно растут
растет,
a0 const.
K ( уменьшается
)
Фазы колебаний, приходящих в точку
Р , от соседних зон Френеля отличаются
на
π
.
Амплитуда результирующего
колебания в точке Р может быть
найдена алгебраически:
A A1 A2 A3 A4 ...
44.
Фазы колебаний, приходящих в точкуР , от соседних зон Френеля отличаются
на
π
.
A A1 A2 A3 A4 ...
можно представить в
виде
Am
Am 1 Am 1
2
A1
2
Вторичные волны гасят друг друга в результате
интерференции
A
A1
2
Действие всей волновой поверхности эквивалентно половине действия одной лишь
центральной зоны (доли мм).
Свет от точки S к точке P распространяется как бы в пределах узкого прямого канала, т.е.
практически прямолинейно.
45.
Как изменится интенсивность света в точке Р, если перегородить часть световогопотока непрозрачным экраном?
перекрыты все
нечётные зоны
Френеля
перекрыты все
чётные зоны
Френеля
Зонные пластинки
Френеля
A
A A2 A4 A6 .... 1
2
Перекрывание ≈ половины светового
потока пластинкой Френеля
Свет распространяется не прямолинейно!
Метод зон Френеля
показывает
A1
A A1 A3 A5 ....
2
Резкое увеличение интенсивности в
точке P
(эффект собирающей линзы, но линзы
нет, среда однородна!)
(1) почему несмотря на волновую природу света наблюдается
его прямолинейное распространение,
(2) что благодаря волновой природе свет может
распространяться в однородной, изотропной среде
непрямолинейно.
46.
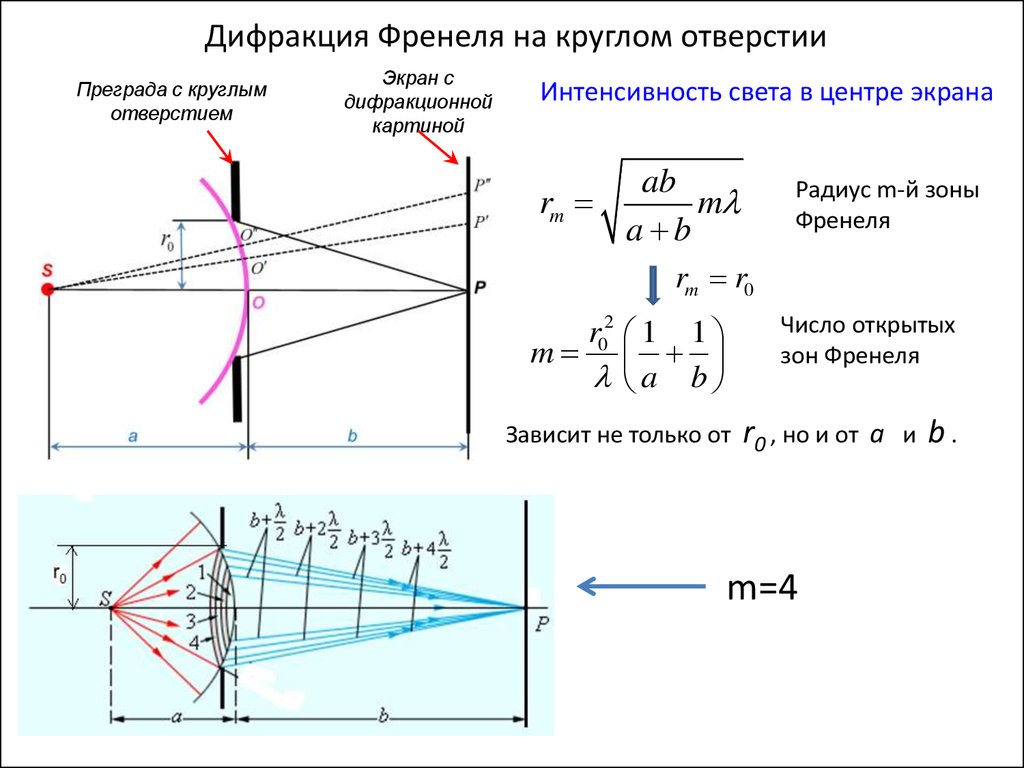
Дифракция Френеля на круглом отверстииПреграда с круглым
отверстием
Экран с
дифракционной
картиной
Интенсивность света в центре экрана
ab
rm
m
a b
Радиус m-й зоны
Френеля
rm r0
r02 1 1
m
a b
Число открытых
зон Френеля
Зависит не только от r0 , но и от a и
m=4
b.
47.
Дифракция Френеля на круглом отверстииИнтенсивность света в центре экрана
r02 1 1
m
a b
A A1 A2 A3 A4 A5 A6 ...
m – чётное
A 0
m – нечётное
A Am
Число открытых
зон Френеля
Амплитуда колебаний в точке P
В центре экрана темно несмотря на отверстие!
A1
Если m невелико Am A1 2
2
Преграда с отверстием, открывающая
небольшое чётное число зон Френеля,
увеличивает амплитуду в центре экрана в ≈ 2,
а интенсивность в ≈4 раза!
Удаление или приближение экрана (b) меняет освещённость в его центре при том же
радиусе отверстия.
48.
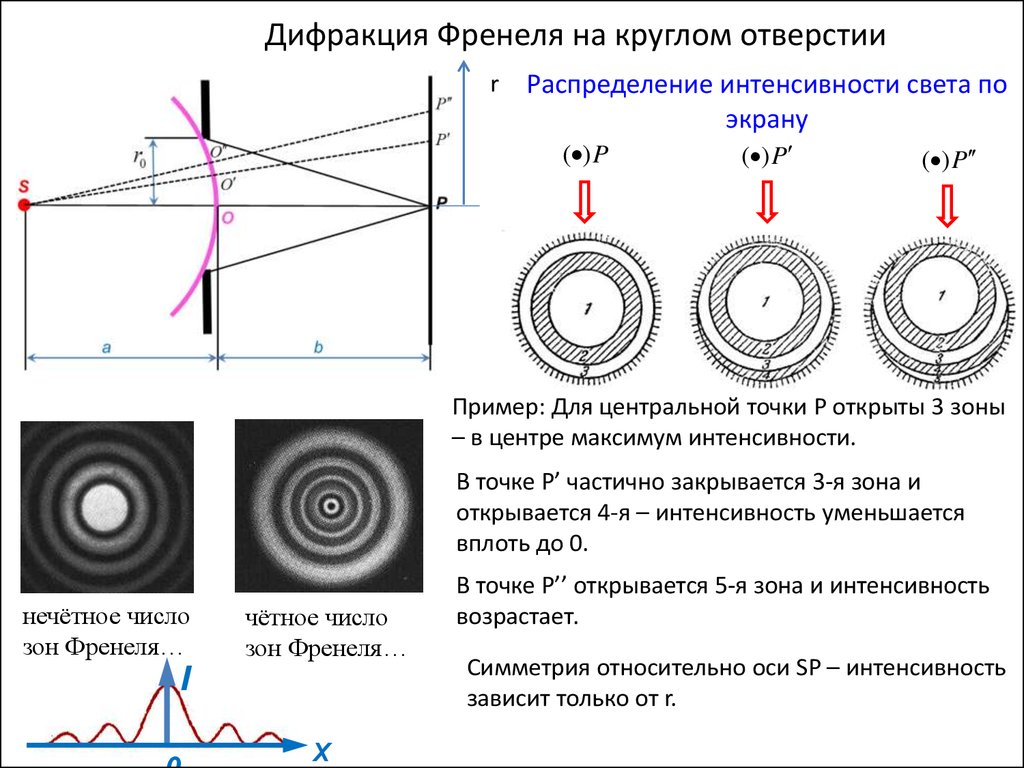
Дифракция Френеля на круглом отверстииr
Распределение интенсивности света по
экрану
( )P
( )P
( )P
Пример: Для центральной точки Р открыты 3 зоны
– в центре максимум интенсивности.
В точке Р’ частично закрывается 3-я зона и
открывается 4-я – интенсивность уменьшается
вплоть до 0.
нечётное число
зон Френеля…
чётное число
зон Френеля…
X
В точке Р’’ открывается 5-я зона и интенсивность
возрастает.
Симметрия относительно оси SP – интенсивность
зависит только от r.
49.
Дифракция лазерного луча с длиной волны 650 нм,прошедшего через отверстие диаметром 0,2 мм
50.
Дифракция Френеля от круглого дискаПусть диск закрывает «т»
первых зон Френеля.
Амплитуда в точке Р:
Таким образом, A
Am 1
0
2
В точке Р всегда светло!! Свет проходит в
область тени!
Дискуссия о природе света, франц академия, 1818
Если m велико (например, большой диск),светлое пятно в
центре исчезает.
Как мал должен быть диск? Несколько зон Френеля, т.е.
диаметр несколько мм. Отнюдь не масштаба λ!!
51.
Дифракция от края преграды.52.
ФРАУНГОФЕР, ЙОЗЕФ(1787–1826)
53.
Оптическая схема для наблюдения дифракции Фраунгофера(дифракция в параллельных лучах) от одной щели.
На бесконечно длинную щель (b<<L) падает плоская монохроматическая
световая волна…
Щель, расположенная
Собирательная линза.
перпендикулярно рисунку.
0
b
Экран, расположенный в
фокальной плоскости линзы.
С
0
b - ширина
щели
54.
Анализ распределения интенсивности света на экране.Р
0
b
О
0
0
По пр.Гюйгенса-Френеля колебания, приходящие на экран от вторичных точечных источников,
расположенных в плоскости щели, в направлении 0 , имеют одинаковую фазу и усиливают
друг друга. Поэтому в центре экрана всегда наблюдается максимум в виде светлой полосы,
параллельной щели.
Лучам от вторичных точечных источников, расположенных в плоскости щели, в направлении 0
соответствует на экране геометрическое место точек (на рис. точка Р ), в виде линии,
параллельной щели. Результирующая интенсивность зависит от соотношения фаз или от
оптической разности хода для лучей рассматриваемого направления.
55.
Рассмотрим параллельные лучи, идущие в направлении 0 Р .Волновую поверхность в плоскости щели разобьем на равные по ширине зоны такие, что разность хода лучей от
краев каждой зоны будет равна половине длины волны («зоны Френеля» в виде полосок).
BC AB sin
n
А
D nb sin
b
С
В
2
2
Опт.разность хода
от краев щели для
рассматриваемого
направления.
Пусть n=1










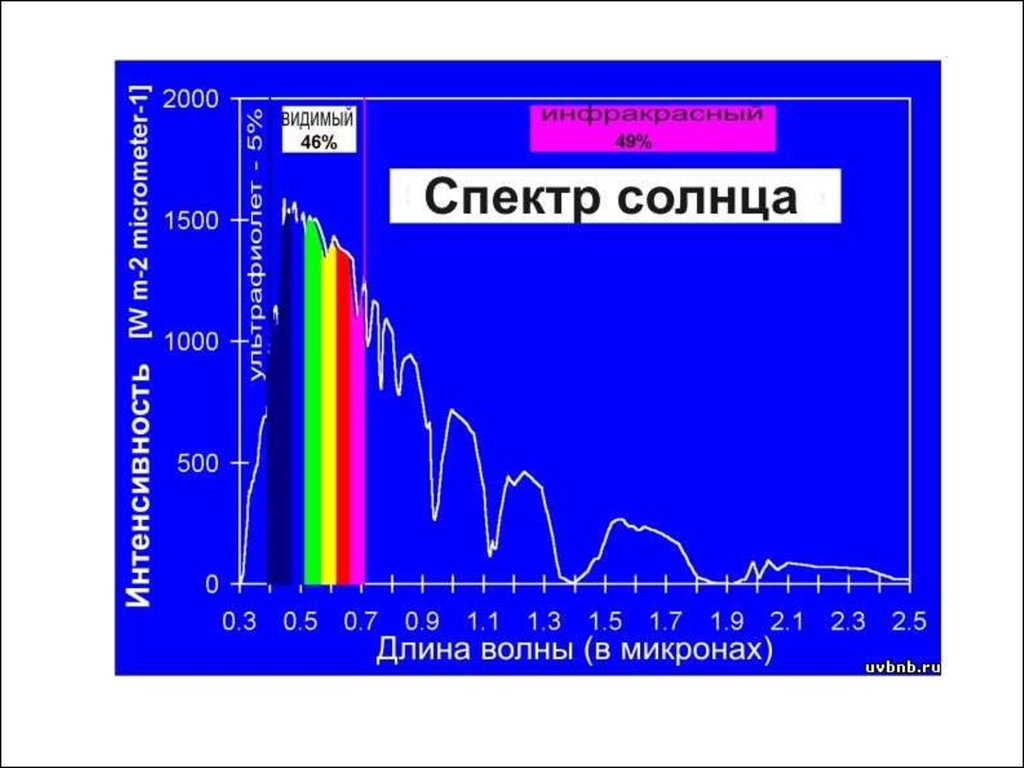





































 Физика
Физика








