Похожие презентации:
Графики тригонометрических функций
1. Графики тригонометрических функций
1. Функция у = sin x, еесвойства
2.Преобразование
графиков
тригонометрических
функций путем
параллельного
переноса
3.Преобразование
ГБОУ СПО НАМТ
Выполинил студент
графиков
группы 14-3 ЭО Алёшин
тригонометрических
Егор
функций путем
сжатия и расширения
2.
Графиком функции у = sin x является синусоидаСвойства функции:
1. D(y) =R
2. Периодическая (Т=2p)
3. Нечетная (sin(-x)=-sin x)
4. Нули функции:
у=0, sin x=0 при х = pn, n Z
y=sin x
3.
Свойства функции у = sin x5. Промежутки знакопостоянства:
У>0 при х (0+2pn; p+2pn), n Z
У<0 при x (-p+2pn; 0+2pn), n Z
y = sin x
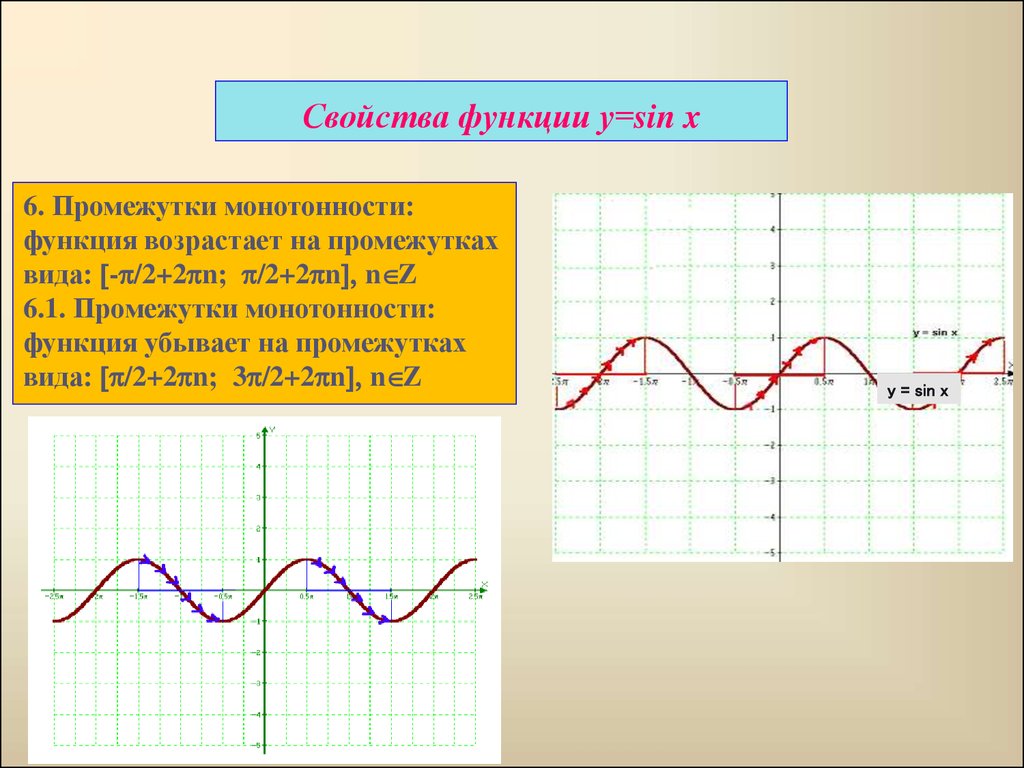
4. Свойства функции у=sin x
6. Промежутки монотонности:функция возрастает на промежутках
вида: [-p/2+2pn; p/2+2pn], n Z
6.1. Промежутки монотонности:
функция убывает на промежутках
вида: [p/2+2pn; 3p/2+2pn], n Z
тригонометрические
функции
y = sin x
5. Свойства функции у =sin x
7. Точки экстремума:Хмах= p/2 +2pn, n Z
Хмin= -p/2 +2pn, n Z
8. Область значений:
Е(у) = [-1;1]
тригонометрические
функции
y=sin x
6. Преобразование графиков тригонометрических функций
График функции у = f (x+в) получается из графика функцииу=f(x) параллельным переносом на (-в) единиц вдоль оси абсцисс
График функции у = f (x)+а получается из графика функции
у=f(x) параллельным переносом на (а) единиц вдоль оси ординат
7.
Графиком функции у = cos x является косинусоидаsin(x+p/2)=cos x
8. Преобразование графиков тригонометрических функций путем сжатия и растяжения
График функции у =k f (x) получается из графика функции у=f(x)путем его растяжения в k раз (при k>1) вдоль оси ординат.
График функции у = k f (x) получается из графика функции
у=f(x) путем его сжатия в k раз (при 0<k<1) вдоль оси ординат.
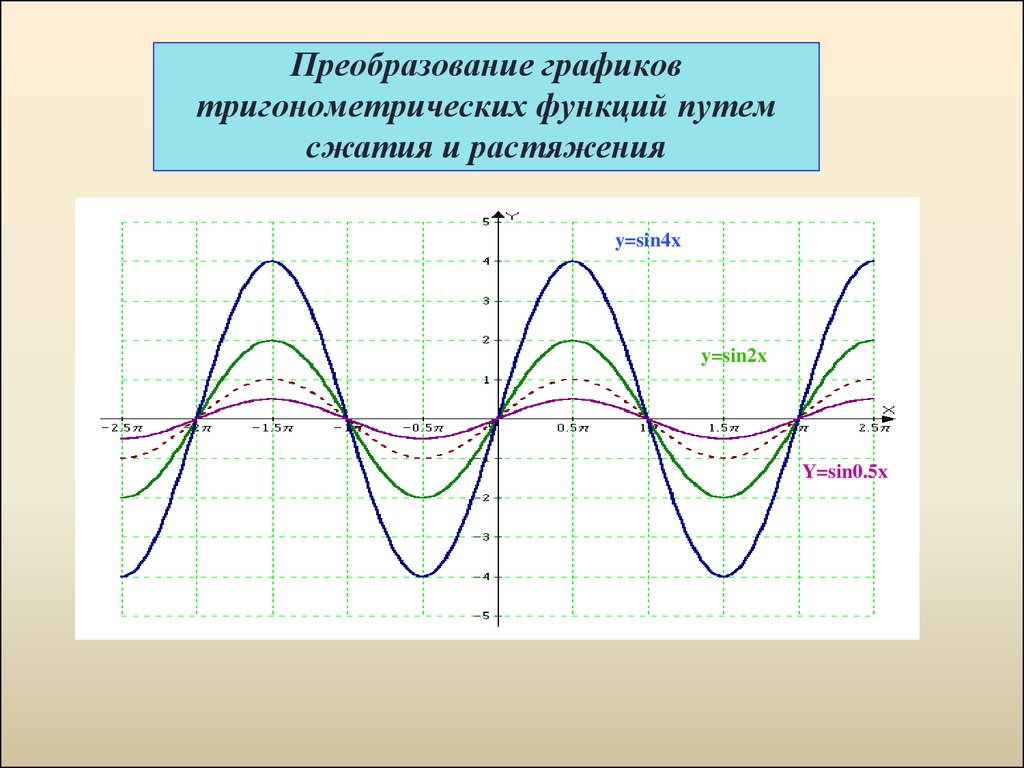
9. Преобразование графиков тригонометрических функций путем сжатия и растяжения
y=sin4xy=sin2x
Y=sin0.5x







 Математика
Математика








