Динамика вращательного движения

1. Динамика вращательного движения

2.

Различают два основных вида вращательного
движения твердого тела:
1. вращение вокруг неподвижной точки О, при
котором все точки тела движутся по поверхностям
концентрических сфер с центром в точке О;
2. вращение вокруг неподвижной оси , при
котором все точки тела вращаются по
окружностям, центры которых лежат на одной
прямой, являющейся осью вращения .

3.

Динамические характеристики поступательного
движения:
1. Сила
F
2. Импульс
p
3. Масса
m
Динамические характеристики вращательного
движения:
1. Момент
2. Момент
3. Момент
силы
импульса
инерции
M
L
J
F
M
p
L
m
J

4. Момент силы -

Момент силы мера воздействия на вращающееся тело.
Момент силы М относительно неподвижной точки
О
равен
векторному
произведению:
M R, F
Направление M совпадает с направлением
поступательного движения правого винта при
вращении его головки от R к F .

5.

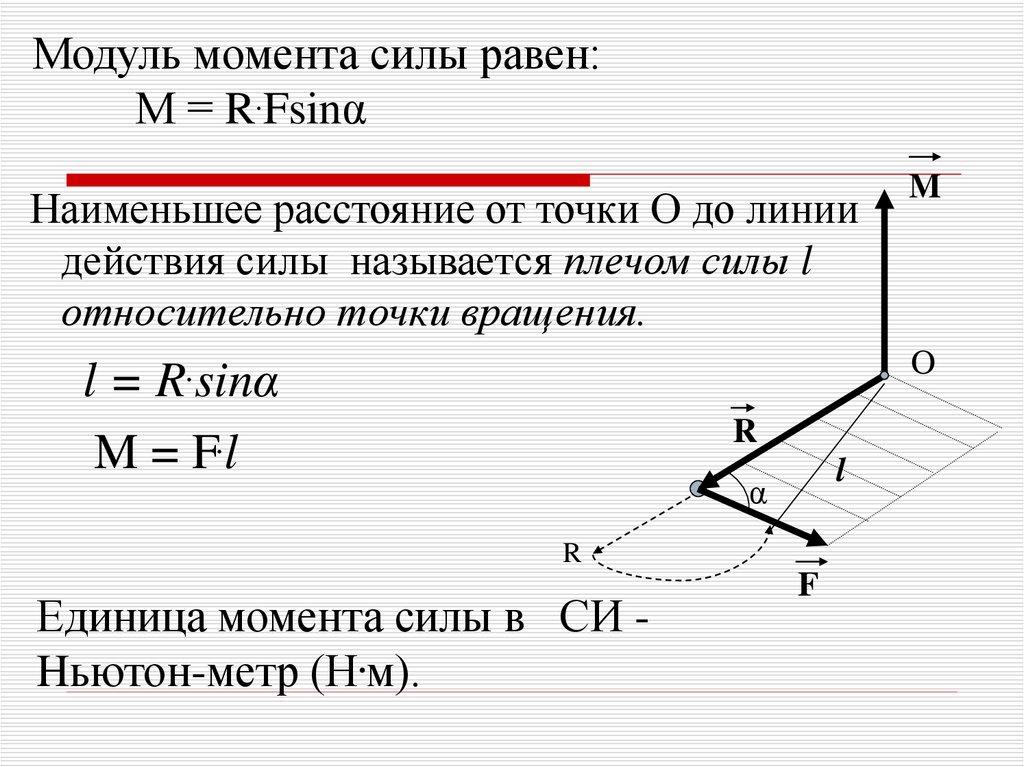
Модуль момента силы равен:
М = R.Fsinα
Наименьшее расстояние от точки О до линии
действия силы называется плечом силы l
относительно точки вращения.
M
O
R.sinα
l=
M = F.l
R
l
α
R
Единица момента силы в СИ Hьютон-метр (Н.м).
F

6.

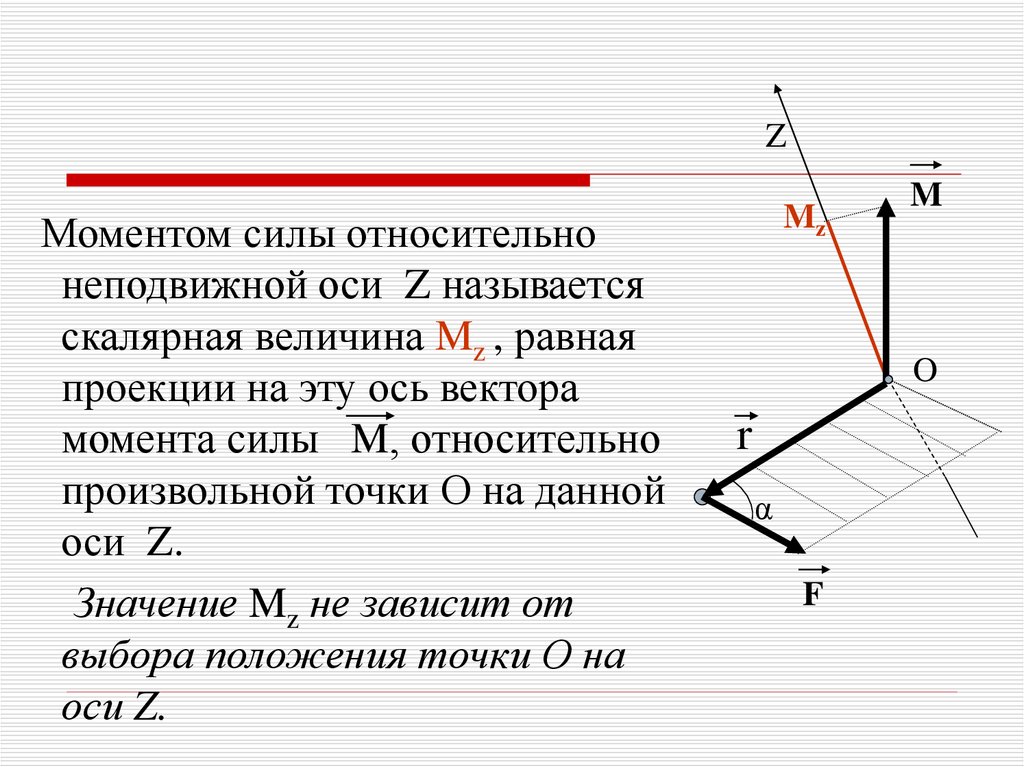
Z
Моментом силы относительно
неподвижной оси Z называется
скалярная величина Mz , равная
проекции на эту ось вектора
момента силы M, относительно
произвольной точки О на данной
оси Z.
Значение Mz не зависит от
выбора положения точки О на
оси Z.
Mz
M
O
r
α
F

7. Момент импульса

Момент импульса – количественная мера
механического движения при вращении тела.
Момент импульса L относительно неподвижного
центра вращения равен векторному произведению
радиуса-вектора на импульс:
L = [ R, mυ ] = [ R,p]
Модуль момента импульса равен:
L= R.m υ.sinα
Единица момента импульса в СИ – кг .м2/с

8.

Моментом импульса
относительно
неподвижной оси Z
называют проекцию
Lz на эту ось момента
импульса относительно
точки O, произвольно
выбранной на этой оси.
Z
L
Lz
R
υ
O

9. Момент инерции

Момент инерции J – мера инертности
вращающегося тела.
Для материальной точки: J = mr2
Для системы материальных точек:
J = ∑mi ri2
Для любого тела:
J = ∫ r2dm

10. Моменты инерции некоторых тел

Момент инерции однородного обруча
Δ
mi
1
2
2
J = (mR1 mR2 ),
2
RR
R
2
При R1 ≈ R2
J mR
Моменты инерции стержня относительно осей,
перпендикулярных стержню и проходящих через центр
масс С и через один из концов стержня А:
С
А
2
ml
JC
;
12
1 2
J A ml
3
ℓ 2

11.

Момент инерции диска:
1
J=
mr2
2
r
Теорема Штейнера: Момент инерции
тела J относительно произвольной оси,
не проходящей через центр масс тела,
равен моменту инерции J0 относительно
l
оси, параллельной данной и проходящей
через центр масс тела O, сложенному с произведением
массы тела m на квадрат расстояния l между осями .
J = Jo + ml2
O

12. Основное уравнение динамики вращательного движения

Cкорость изменения вектора момента импульса
тела относительно неподвижного центра вращения
равна действующему на тело результирующему
вектору момента внешних
сил,
относительно
того
же центра:
dL
М=
dt
L = Jω
(сравни: р = mυ ), следовательно:
d J
М=
dt

13.

При вращении вокруг неподвижной оси:
d
Мz =
( J z )
dt
Для системы тел, вращающихся вокруг
неподвижного центра:
d n
М ( J i i )
dt i 1

14. Закон сохранения момента импульса

Если М = 0 (система замкнута):
d n
М ( J i i ) = 0
dt i 1
n
d
( J i i ) 0,
J i i const
dt
i 1
В замкнутой системе суммарный момент
импульса есть величина постоянная

15. Работа при вращении твердого тела. Кинетическая энергия вращающегося тела

Если под действием внешней силы Fτ тело поворачивается на
угол dφ, то элементарная работа этой силы
A F rd Md
Полная работа при повороте на угол φ
А Мd
0
Кинетическая энергия вращающегося тела вычисляется по
формуле
J 2
Wк
2
Работа равна изменению кинетической
энергии:
2
2
J 2 J 1
А = ∆Wк =
2
2

16. Кинетическая энергия тела катящегося без проскальзывания

Кинетическая энергия катящегося тела
mv 2 J 2
Wкатящ c c
2
2
где т — масса катящегося тела;
vс — скорость центра масс тела;
J с - момент инерции тела относительно
оси, проходящей через его центр масс;
- угловая скорость тела.