Свойства функции

1.

1 0 . 4 . 1 . 4
У М Е Т Ь
З А Д А Н Н О М У
О П И С Ы ВАТ Ь
Г РАФ И К У
П О
ФУ Н К Ц И И
С ВО Й СТ ВА
С ВО Й СТ ВА
ФУНКЦИИ
Е Ё

2.

1) ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ;
2 ) О БЛ АСТ Ь З Н АЧ Е Н И Й ФУ Н К Ц И И ;
3) НУЛИ ФУНКЦИИ;
4) ПЕРИОДИЧНОСТЬ ФУНКЦИИ;
5) ПРОМЕЖУТКИ МОНОТОННОСТИ
ФУНКЦИИ;
6) ПРОМЕЖ УТКИ ЗНАКОПОСТОЯНСТВА
ФУНКЦИИ;
7) НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ
З Н АЧ Е Н И Я ФУ Н К Ц И И ;
8) ЧЕТНОСТЬ, НЕЧЕТНОСТЬ ФУНКЦИИ;
9 ) О Г РА Н И Ч Е Н Н О СТ Ь ФУ Н К Ц И И ;
10) НЕПРЕРЫВНОСТЬ ФУНКЦИИ;
11) ЭКСТРЕМУМЫ ФУНКЦИИ

3.

Определение функции
Зависимость между двумя переменными х и у,
при котором каждому значению переменной х соответствует
единственное значение переменной у называют функцией .
Обозначают у = f(х),
у
у
где х – независимая
переменная (аргумент),
у
у2
у = f(x) – зависимая переменная (функция).у1
хо
у1
хо
О
у2
Не является функцией
х1
О
х
х
у1
О
х2
х
у2
Не является функцией
Является функцией

4.

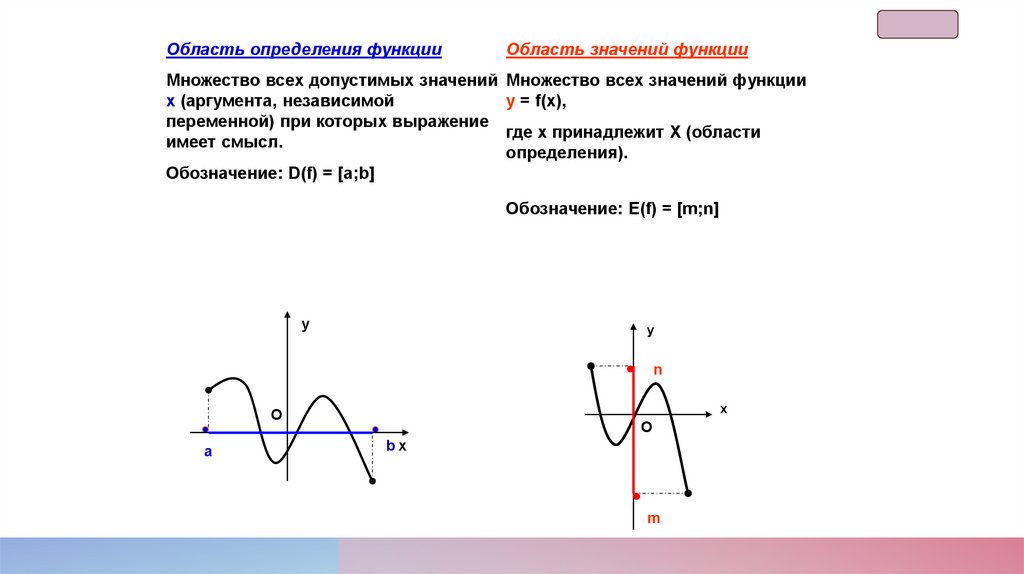
Область определения функции
Область значений функции
Множество всех допустимых значений Множество всех значений функции
х (аргумента, независимой
у = f(х),
переменной) при которых выражение
где х принадлежит Х (области
имеет смысл.
определения).
Обозначение: D(f) = [а;b]
Обозначение: Е(f) = [m;n]
у
у
n
х
О
a
О
bх
m

5.

Функция, заданная в виде многочлена

6.

Дробно-рациональная функция

7.

Иррациональная функция

8.

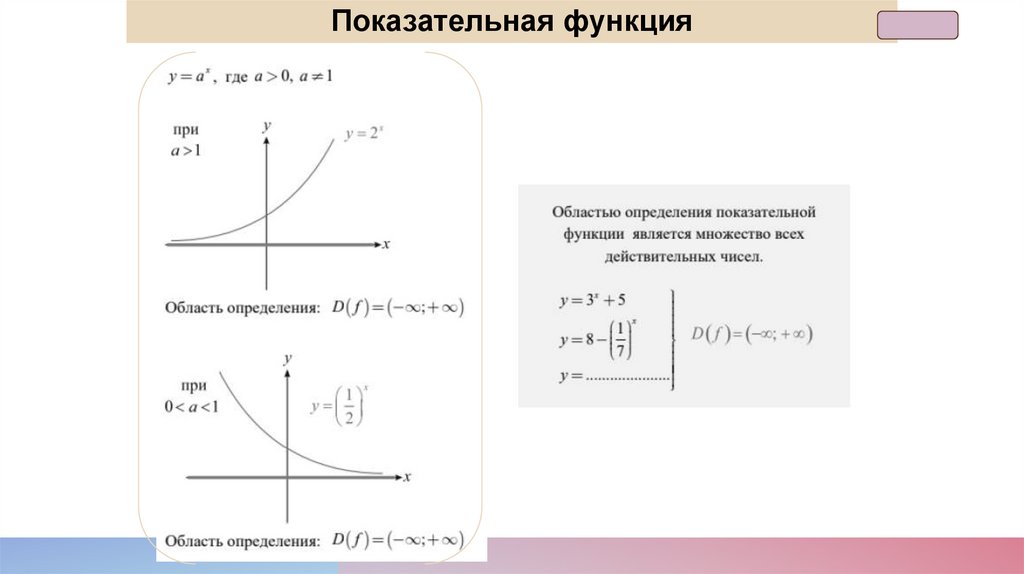
Показательная функция

9.

Тригонометрические функции

10.

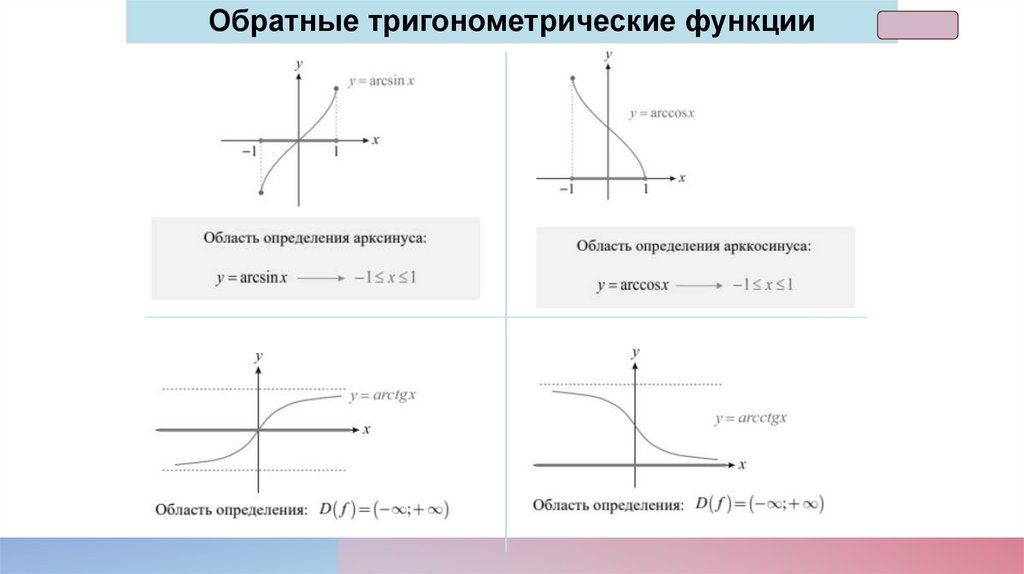
Обратные тригонометрические функции

11.

12.

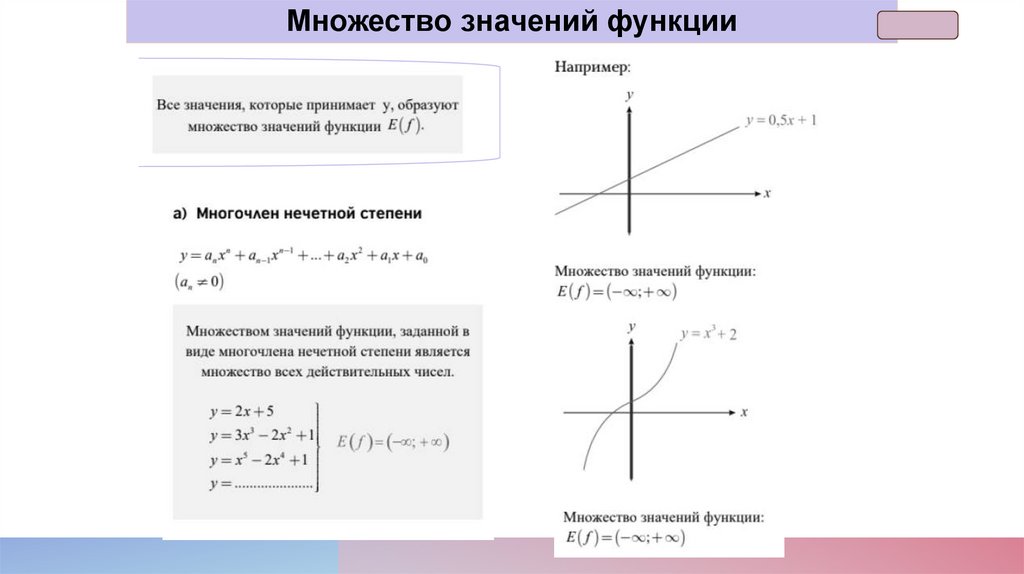
Множество значений функции

13.

Множество значений функции

14.

Множество значений функции

15.

Множество значений функции

16.

Множество значений функции

17.

18.

СВО Й СТВА ФУНКЦ И И
•Возрастание
•Убывание
Функцию у = f(x) называют
возрастающей на множестве D(f), если
для любых двух точек х1 и х2 области
определения, таких, что х1 < х2 ,
выполняется неравенство f(x1 ) < f(x2).
Функцию у = f(x) называют убывающей
на множестве D(f), если для любых
двух точек х1 и х2 области
определения, таких, что
х1 < х2 ,
выполняется неравенство f(x1 ) > f(x2).
(Если большему значению аргумента
соответствует большее значение
функции)
(Если большему значению аргумента
соответствует меньшее значение
у
функции)
у
О
О
x
x
Термины «возрастающая», «убывающая» функция объединяют
общим названием МОНОТОННАЯ ФУНКЦИЯ.

19.

ОГРАНИЧЕННОСТЬ
ФУНКЦИИ
• Функцию у = f(x) называют
ограниченной снизу на множестве
D(f), если все значения функции на
области определения больше
некоторого числа.
• Функцию у = f(x) называют
ограниченной сверху на множестве
D(f), если все значения функции на
области определения меньше
некоторого числа.
(Если существует число m такое, что для
(Если существует число m такое, что для
любого значения х области определения
выполняется неравенство f(x) < m.)
любого значения х области определения
выполняется неравенство f(x) > m.)
у
m
у
О
m
x
О
Если функция ограничена снизу, то ее
график целиком расположен выше
некоторой горизонтальной прямой
у = m.
x
Если функция ограничена сверху, то
ее график целиком расположен ниже
некоторой горизонтальной прямой
у = m.
Если функция ограниченна и сверху и снизу, то ее называют
ограниченной.

20.

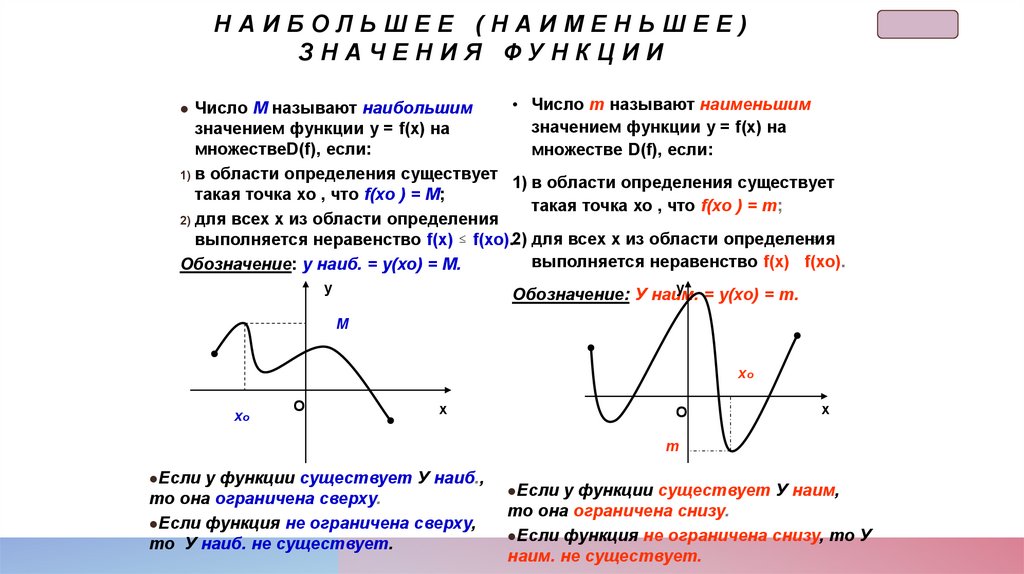
НАИБОЛЬШЕЕ (НАИМЕНЬШЕЕ)
ЗНАЧЕНИЯ ФУНКЦИИ
Число M называют наибольшим
• Число m называют наименьшим
значением функции у = f(x) на
множестве D(f), если:
значением функции у = f(x) на
множествеD(f), если:
1) в области определения существует
1) в области определения существует
такая точка хо , что f(хо ) = M;
такая точка хо , что f(хо ) = m;
2) для всех х из области определения
выполняется неравенство f(x) f(хо).2) для всех х из области определения
выполняется неравенство f(x) f(хо).
Обозначение: у наиб. = у(хо) = M.
у
у
Обозначение: У наим.
= у(хо) = m.
M
хо
хо
О
х
О
х
m
Если у функции существует У наиб.,
то она ограничена сверху.
Если функция не ограничена сверху,
то У наиб. не существует.
Если у функции существует У наим,
то она ограничена снизу.
Если функция не ограничена снизу, то У
наим. не существует.

21.

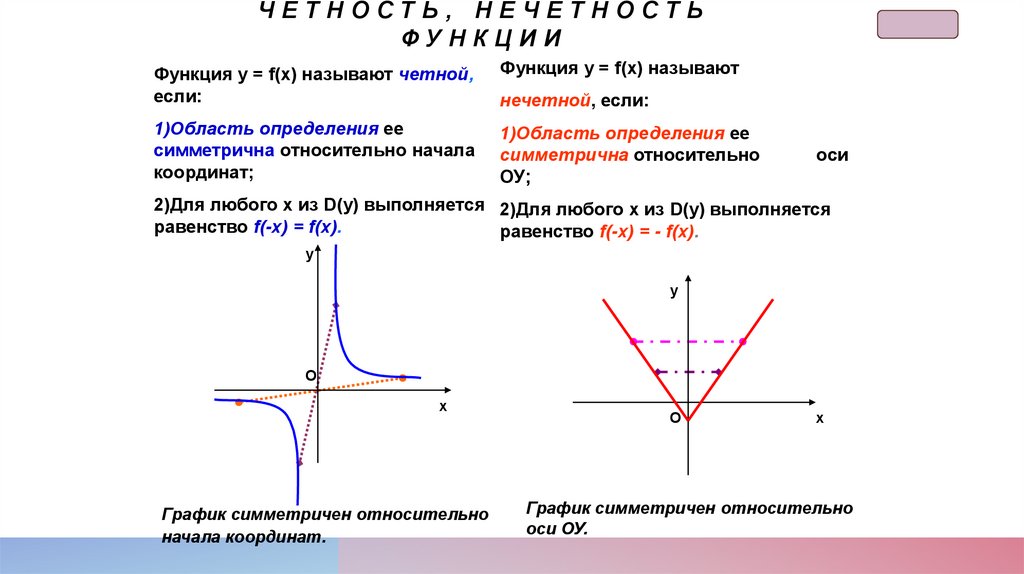
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ
ФУНКЦИИ
Функция у = f(х) называют четной,
если:
Функция у = f(х) называют
1)Область определения ее
симметрична относительно начала
координат;
1)Область определения ее
симметрична относительно
ОУ;
нечетной, если:
оси
2)Для любого х из D(у) выполняется 2)Для любого х из D(у) выполняется
равенство f(-x) = f(x).
равенство f(-x) = - f(x).
у
у
О
x
График симметричен относительно
начала координат.
О
x
График симметричен относительно
оси ОУ.

22.

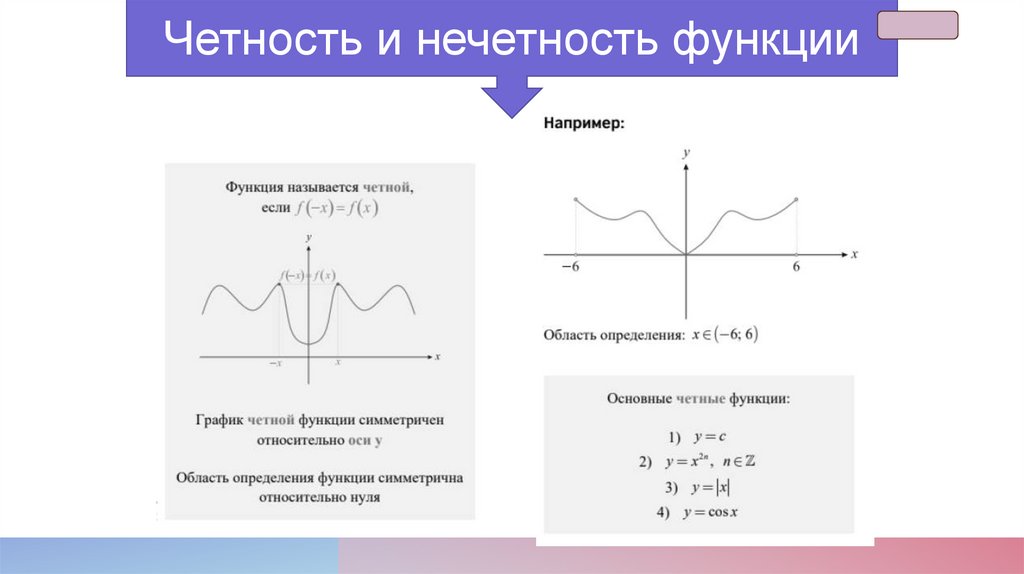
Четность и нечетность функции

23.

Четность и нечетность функции

24.

Четность и нечетность функции

25.

10/18/2024
25

26.

Л И Н Е Й Н А Я Ф У Н К Ц ИyЯ kx m( k 0)
K>0
у
1. D(f) = R;
2. Не является ни четной ни
нечетной;
m
О
3. Если k > 0, возрастает,
если k < 0 убывает;
х
4. Не ограничена ни снизу, ни
сверху;
5. Нет ни наибольшего, ни
наименьшего значения;
у
K<0
m
6. Функция
Е( f ) непрерывна;
,0 0,
7.
8. Не имеет выпуклости.
О
х

27.

ФУНКЦИЯ
D( f ) ,0 0,
1.
k
y
x
у
K>0
2. Нечетная функция;
3. Если k > 0, то функция убывает на D(f),
О
если k < 0, то функция возрастает на D(f);
x
4. Не ограничена ни сверху, ни снизу;
5. Нет ни наименьшего, ни наибольшего значений;
6. Функция терпит разрыв в точке х = 0;
7.
у
Е( f ) ,0 0,
K<0
8. Если k > 0, то функция выпукла вверх при х < 0,
и выпукла вниз при х > 0;
Если k < 0, то функция выпукла вверх при х > 0,
и выпукла вниз при х < 0.
О
х

28.

y x
ФУНКЦ И Я
1. D(f) = [0; + ∞);
у
2. Не является ни четной ни нечетной;
3. Возрастает;
4. Не ограничена ни снизу, ни сверху;
5. Наибольшего значения нет, наименьшее
значение 0, при х = 0;
6. Функция непрерывна;
7. Е(f) = [0; + ∞)
8. Выпукла вверх.
О
х

29.

y x
ФУНКЦ И Я
1. D(f) = R;
2. Функция четная;
у
3. Возрастает на [0; + ∞);
убывает ( - ∞; 0]
4. Не ограничена сверху,
ограничена снизу;
5. Наибольшего значения нет,
наименьшее значение 0, при х = 0;
6. Функция непрерывна;
7. Е(f) = [0; + ∞)
8. Выпукла вниз.
О
х

30.

ФУНКЦ И Я
у ах
1. D(f) = R;
2. Функция четная;
3. Возрастает на [0; + ∞); убывает (
- ∞; 0]
4. Не ограничена сверху,
ограничена снизу;
5. Наибольшего значения нет,
наименьшее значение 0,
при
х = 0;
6. Функция непрерывна;
7. Е(f) = [0; + ∞)
8. Выпукла вниз.
у
2
1. D(f) = R;
2. Функция четная;
3. Убывает на [0; + ∞);
возрастает ( - ∞; 0]
4. Не ограничена снизу,
ограничена сверху;
5. Наименьшего значения нет,
наибольшее значение 0,
при х = 0;
6. Функция непрерывна;
7. Е(f) = ( - ∞; 0];
8. Выпукла вверх.
О
у
х
a>0
a<0
О
х

31.

ИССЛЕДУЙТЕ ФУНКЦИЮ ПО
Г РАФ И К У

32.

Периодичность функции

33.

Периодичность функции

34.

Периодичность функции

35.

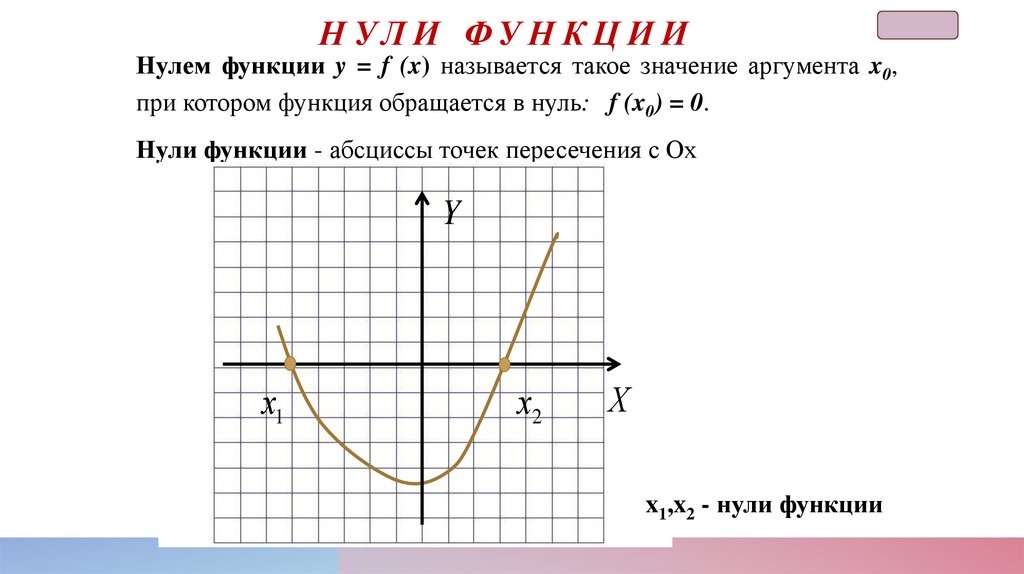
Н УЛ И ФУ Н К Ц И И
Нулем функции y = f (x) называется такое значение аргумента x0,
при котором функция обращается в нуль: f (x0) = 0.
Нули функции - абсциссы точек пересечения с Ох
Y
х1
х2
Х
x1,x2 - нули функции

36.

ПРОМЕЖУТКИ
ЗНАКОПОСТОЯНСТВА
Промежутки, на которых непрерывная функция сохраняет свой
знак и не обращается в нуль, называются
промежутками знакопостоянства.
y > 0 (график расположен
выше оси ОХ)
при х (- ∞; 1) U (3; +∞),
y<0 (график расположен
ниже OX) при х (1;3)
y
1
0 1
x