Предел функции в точке

1. Понятие предела функции в точке

2. Основные вопросы:

• Определение предела функции в точке,
бесконечно малой и бесконечно большой
функции в точке. Связь между
б/малыми и б/большими функциями в
точке.
• Основные теоремы о пределах функций
(суммы, произведения и частного).
21.09.2021
2

3. Предел функции

–
одно
из
основных
понятий
математического анализа. Понятие предела использовалось
еще Ньютоном во второй половине XVII века и математиками
XVIII века, такими как Эйлер и Лагранж, однако они понимали
предел интуитивно. Первые строгие определения предела дали
Больцано в 1816 году и Коши в 1821 году.

4.

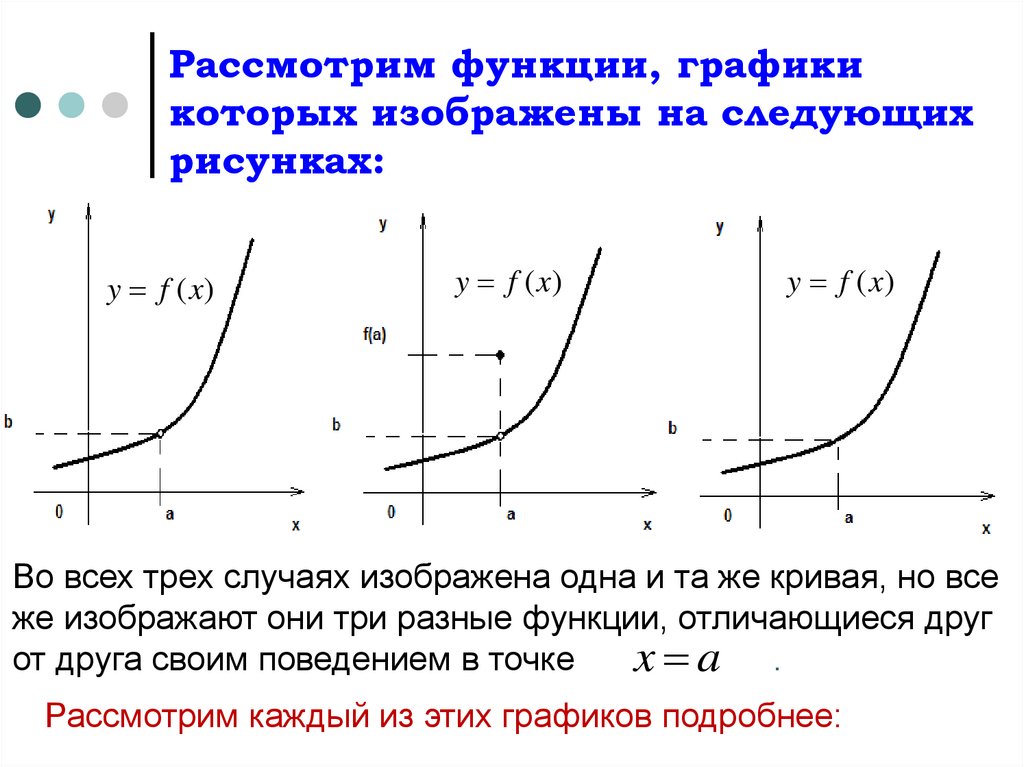
Рассмотрим функции, графики
которых изображены на следующих
рисунках:
y f (x)
y f (x)
y f (x)
Во всех трех случаях изображена одна и та же кривая, но все
же изображают они три разные функции, отличающиеся друг
от друга своим поведением в точке
x a .
Рассмотрим каждый из этих графиков подробнее:

5.

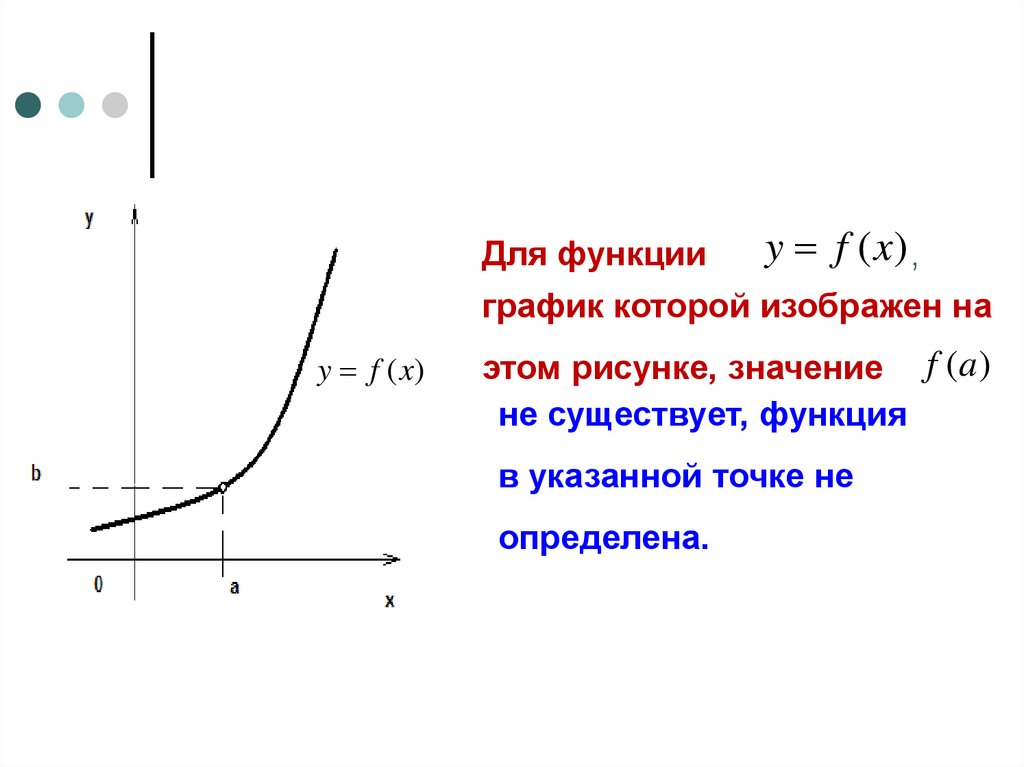
Для функции
y f (x) ,
график которой изображен на
y f (x)
этом рисунке, значение f (a )
не существует, функция
в указанной точке не
определена.

6.

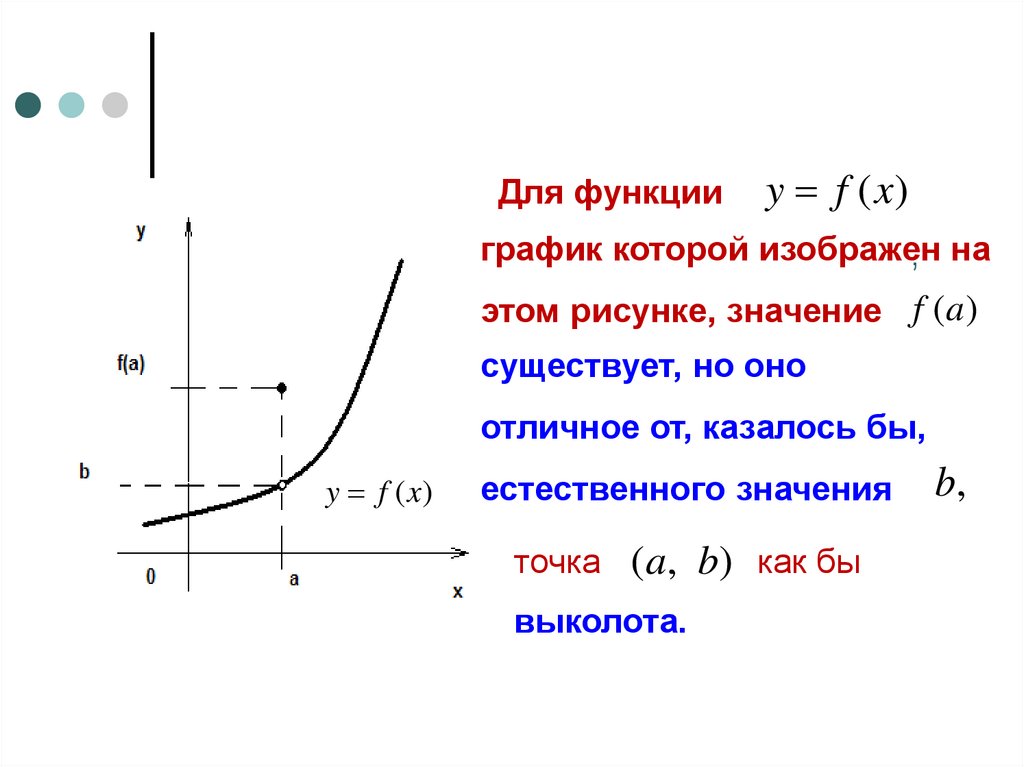
Для функции
y f (x)
график которой изображен
, на
этом рисунке, значение f (a )
существует, но оно
отличное от, казалось бы,
y f (x)
естественного значения
точка (a, b) как бы
выколота.
b,

7.

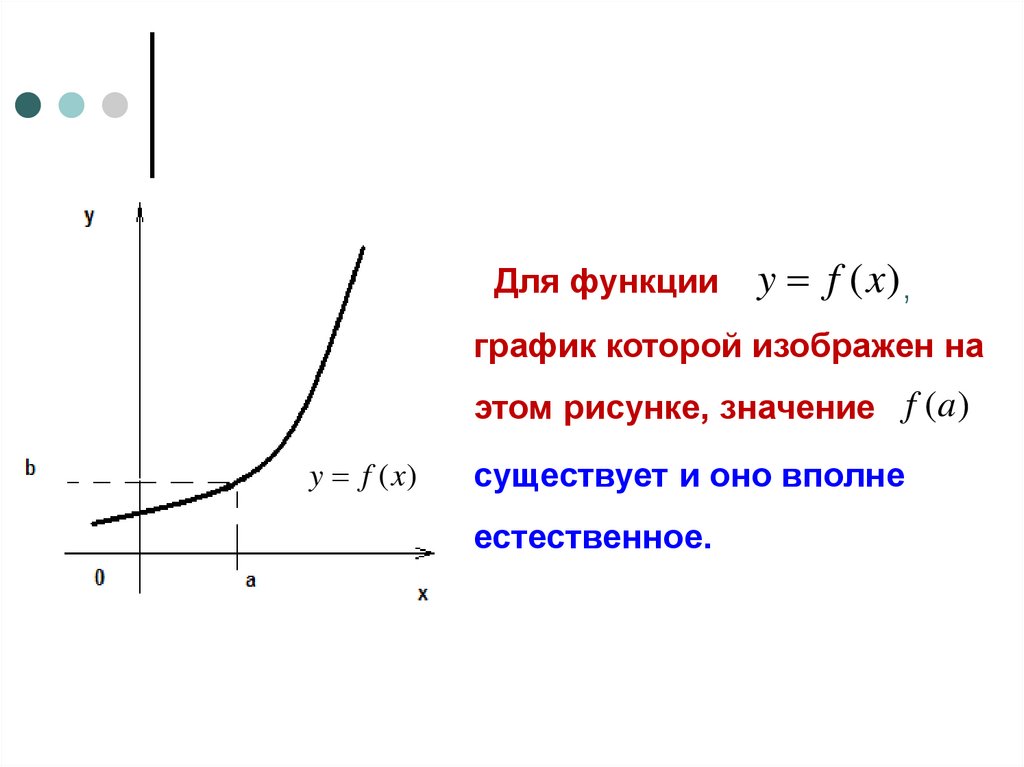
Для функции
y f (x) ,
график которой изображен на
этом рисунке, значение f (a )
y f (x)
существует и оно вполне
естественное.

8.

Для всех трех случаев используется одна и
та же запись:
lim f ( x) b,
x а
которую читают: «предел функции y f (x) при
стремлении x к a равен b ».
Содержательный смысл этой фразы следующий: если значения
аргумента выбирать все ближе и ближе к значению
x a, то значения функции все меньше и меньше
отличаются от предельного значения b.
Или можно сказать так: в достаточно малой окрестности
точки a справедливо приближенное равенство:
f ( x) a
При этом сама точка
x a исключается из рассмотрения.

9. Предел функции в точке

Число В называется пределом
функции в точке а, если для всех
значений х , достаточно близких к а
и отличных от а, значение функции
f (x) сколь угодно мало отличается
от В.
lim f ( x ) b
x a

10. Предел функции в точке

Пусть функция y = f(x) определена в некоторой окрестности точки
x0, кроме, быть может самой точки x0.
Число А называют пределом функции в точке x0 (или при x x0),
если для любого положительного ε найдется такое положительное
число δ, что для всех х из δ – окрестности точки x0 справедливо
неравенство:
f (x) A
0; 0; x : x x0 f ( x ) A
lim f ( x ) A
x x0

11. Предел функции в точке

0; 0; x : x x0 f ( x ) A
ε окрестность точки А
y
2
А
0
х0
х
δ окрестность точки x0
Геометрический смысл предела: для всех х из δ – окрестности точки
x0 точки графика функции лежат внутри полосы, шириной 2ε,
ограниченной прямыми: у = А + ε , у = А - ε .

12. Односторонние пределы

В определении предела функции
lim f ( x ) A
x x0
предполагается, что x стремится к x0 любым способом: оставаясь
меньше, чем x0 (слева от x0), большим, чем x0 (справа от x0), или
колеблясь около точки x0.
Бывают случаи, когда способ приближения аргумента x к x0
существенно влияет на значение предела, поэтому вводят понятия
односторонних пределов.
Число А1 называют пределом функции слева в точке x0, если для
любого ε > 0 найдется такое δ >0, что для всех
x ( x0 ; x0 )
справедливо неравенство:
f ( x ) A1
Предел слева записывают так:
lim f ( x ) A1
x x0 0

13. Односторонние пределы

Число А2 называют пределом функции справа в точке x0, если
0; 0; x x0 ; x0 f ( x ) A2
Предел справа записывают так:
Пределы функции слева и
справа называют
односторонними пределами.
y
А2
А1=А2=А
А1
0
lim f ( x ) A2
x x0 0
Очевидно, если существует
х0
х
lim f ( x ) A
x x0
то существуют и оба
односторонних предела,
причем А = А1 = А2

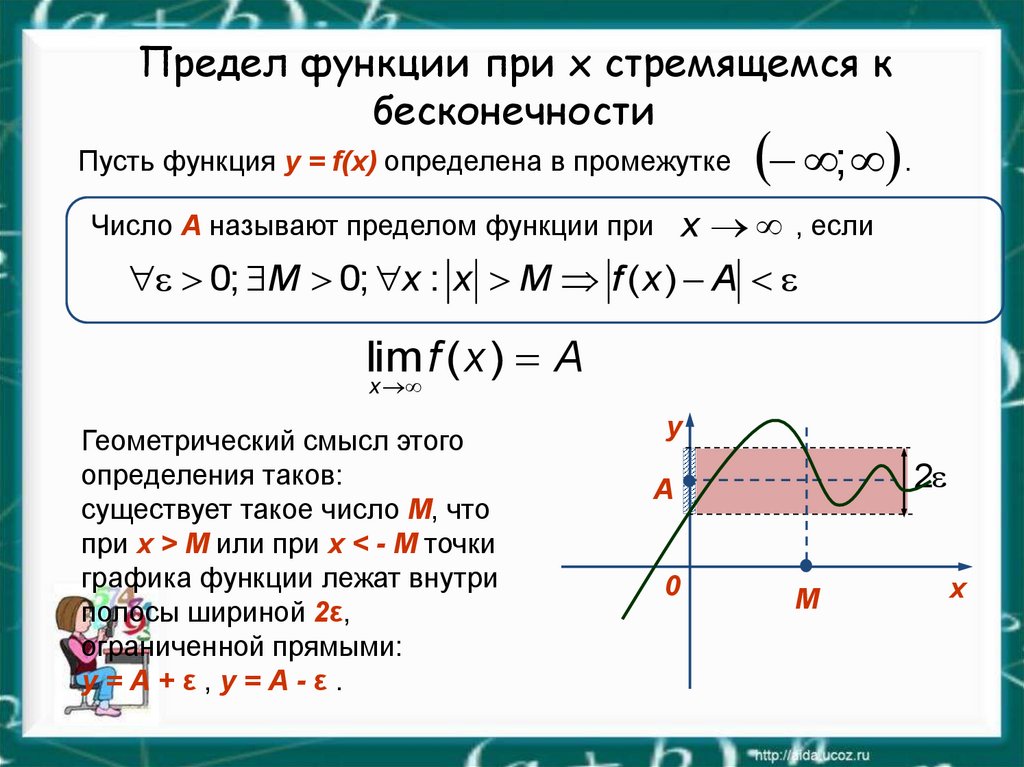
14. Предел функции при x стремящемся к бесконечности

Пусть функция y = f(x) определена в промежутке
; .
x
Число А называют пределом функции при
, если
0; M 0; x : x M f ( x ) A
lim f ( x ) A
x
Геометрический смысл этого
определения таков:
существует такое число М, что
при х > M или при x < - M точки
графика функции лежат внутри
полосы шириной 2ε,
ограниченной прямыми:
у=А+ε,у=А-ε.
y
2
А
0
М
х

15. Теорема.

15

16. Бесконечно малая функция и бесконечно большая функция.

• Функция α (x) называется бесконечно
малой при x → a (здесь a – конечное число
или ∞), если
• Функция f(x) называется бесконечно
большой функцией (или бесконечно
большой величиной) при х→а, если
lim f ( x)
x a
16

17. Графическая иллюстрация

• х →0
х
1
х
1
у 0
х
Таким образом, величина, обратная
бесконечно малой, есть бесконечно
большая, и наоборот.
17

18.

lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0

19.

lim C C
x x0

20.

lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0

21.

lim f ( x)
f ( x) x x0
lim
, если _ lim g ( x) 0
x x0 g ( x)
x x0
lim g ( x)
x x0

22.

lim (k f ( x)) k lim f ( x)
x x0
x x0

23.

lim ( z ) (lim z)
n
x a
x a
n

24. Вычисление пределов

Вычисление
lim f ( x ) A
x x0
предела:
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому
числу.
3x 1 3 1 1 2
lim
2
2
x 1
1
x
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0

25. Вычислить пределы:

lim ( x 2 7 x 4) 32 7 3 4 8;
x 3
x 4
( x 2)( x 2)
x 2
lim 2
lim
lim
2;
x 2 x 2 x
x 2
x 2
x( x 2)
x
3
2
(
x
2
)(
x
)
2
(0 / 0)
2x 7x 6
2x 3
2
lim
lim
lim
;
2
2
x 2
x 2
x 2 x 2
( x 2)
( x 2)
2

26.

Примеры

27. Вычисление пределов

Часто при подстановке предельного значения x0 в функцию f(x)
получаются выражения следующих видов:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ; 0 ;
Эти выражения называются неопределенности, а вычисление
пределов в этом случае называется раскрытие
неопределенности.

28. Методы вычисления пределов на неопределенность

3x 2 x 0 0 0
lim 2
x 0 2 x 5 x
0 0 0
2
0 с с
, ,
0 0

29.

• В большинстве случаев, чтобы раскрыть
0
неопределенность вида
,
0

30.

3x 2 x 0
lim 2
x 0 2 x 5 x
0
2
Разложим числитель и знаменатель на
множители:
x 3x 2
3x 2 2
lim
lim
x 0 x 2 x 5
x 0 2 x 5
5

31.

lim 4 x
4x
4*0
0
x 0
lim 2
2
x 0 3 x 2 x
lim 3x 2 x 3 * 0 2 * 0 0
x 0
4x
4
4
lim
lim
2.
x 0 x 3 x 2
x 0 3 x 2
3* 0 2

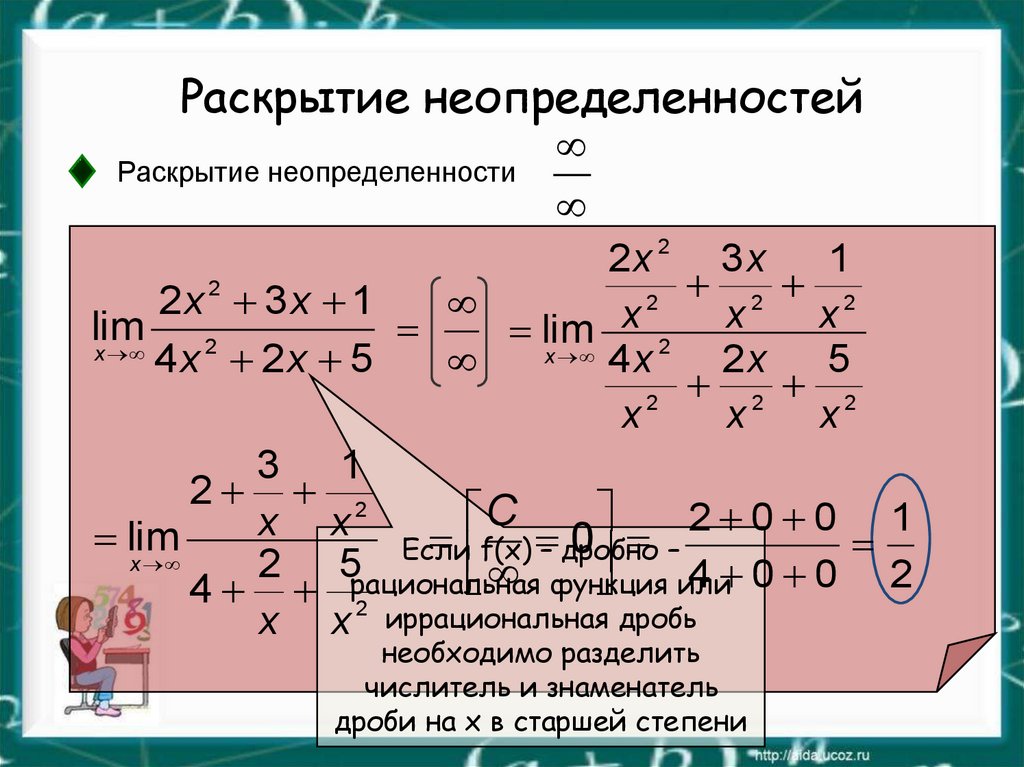
32. Раскрытие неопределенностей

Раскрытие неопределенности
0
0
x 2 14 x 32
0
x 2 x 16
lim 2
lim
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Если f(x) – дробно –
рациональная
x 1 1 x 1 1
0
x 1 1 функция,
наlim Если f(x) – иррациональная
lim необходимо разложить
x 0
0
множители
числитель
иx 0 дробь, x
x
x 1 умножить
1
необходимо
знаменатель дроби
числитель и знаменатель
x 1 1
1дроби на выражение,
1
lim
lim
числителю.
x 0
x 0
сопряженное
x x 1 1
x 1 1 2

33. Раскрытие неопределенностей

Раскрытие неопределенности
2x 2 3 x 1
2 2
2
2x 2 3 x 1
x
x
x
lim 2
lim
x
x 4 x 2
2x 5
4 x 2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
f(x) – дробно
0 –
Если
x
2 5рациональная
4 0 0 2
функция
или
4 2
x x иррациональная дробь
необходимо разделить
числитель и знаменатель
дроби на x в старшей степени

34.

• Чтобы раскрыть неопределенность
данного вида, зависящую от
иррациональности,

35. Раскрытие неопределенностей

Раскрытие неопределенности
lim x 2 1 x 2 1
x
lim
x
lim
x
x 1 x 1
2
2
2
Умножим и разделим
2
1)
функцию
на
сопряженное
lim
2
x
2
выражение.
x 1 x 1
2
2
0
2
x2 1 x2 1
( x 1) ( x
2
x 1 x 1
2
x 1 x 1
2

36. Первый замечательный предел

Функция
sin x
x
не определена при x = 0.
Найдем предел этой функции при
М С
x
О В А
OA 1
x 0
0 x
2
Обозначим:
S1 - площадь треугольника OMA,
S2 - площадь сектора OMА,
S3 - площадь треугольника OСА,
Из рисунка видно, что S1< S2 < S3
1
1
1
S1 OA MB OA 0M sin x sin x
2
2
2

37. Первый замечательный предел

М С
x
О В А
1
1
S2 OA AM x
2
2
1
1
S3 OA AC 1 tgx
2
2
1
1
1
sin x x tgx
2
2
2
x tgx
x sin x
sin x x tgx
sin x
cos x x
sin x
1
x
sin x
cos x
1
x

38. Первый замечательный предел

sin x
cos x
1
x
lim cos x cos 0 1
x 0
lim1 1
sin x
lim
1
x 0
x
x 0
Формула справедлива также при x < 0
Следствия:
x
lim
1
x 0
sin x
tgx
lim
1
x 0
x
x
lim
1
x 0
tgx
sin kx
lim
1
x 0
kx

39. Первый замечательный предел

0
1 cos 4 x
2 sin 2x
sin 2 x
lim
lim
2 lim
2
2
x 0
x
0
x
0
0
x
x
x
2
2
sin 2 x 2 lim 2 sin 2 x
x 0
2 lim
2x
x 0 x
2
2
sin 2 x
2
2 2 lim
2 2 1 8
x 0
2x
2