Множества

1.

Способы задания множества
1) перечисление всех его элементов
A={1,5};
2) с помощью характеристического свойства его элементов
A={x | x – четное число}.
Пустое множество – –
множество, не содержащее ни одного элемента.
Универсальное множество или универсум – U –
множество, содержащее все элементы, находящиеся в рассмотрении.
«a A» «элемент a принадлежит множеству A»
«для элемента a выполняется
характеристическое свойство множества A».
«a A» «элемент a не принадлежит множеству A» или
«для элемента a не выполняется
характеристическое свойство множества A».
1

2.

«A B» « B A» «A подмножество B»
«все элементы множества A принадлежат множеству B»
и B – несобственные подмножества множества B,
остальные подмножества – собственные.
«A=B» « A и B равные (совпадающие) множества »
«B A и A B»
Булеан множества A – P A ={B|B A} –
совокупность всех подмножеств множества A.
2

3.

Операции теории множеств
На булеане P U определяются операции над множествами
A P U и B P U .
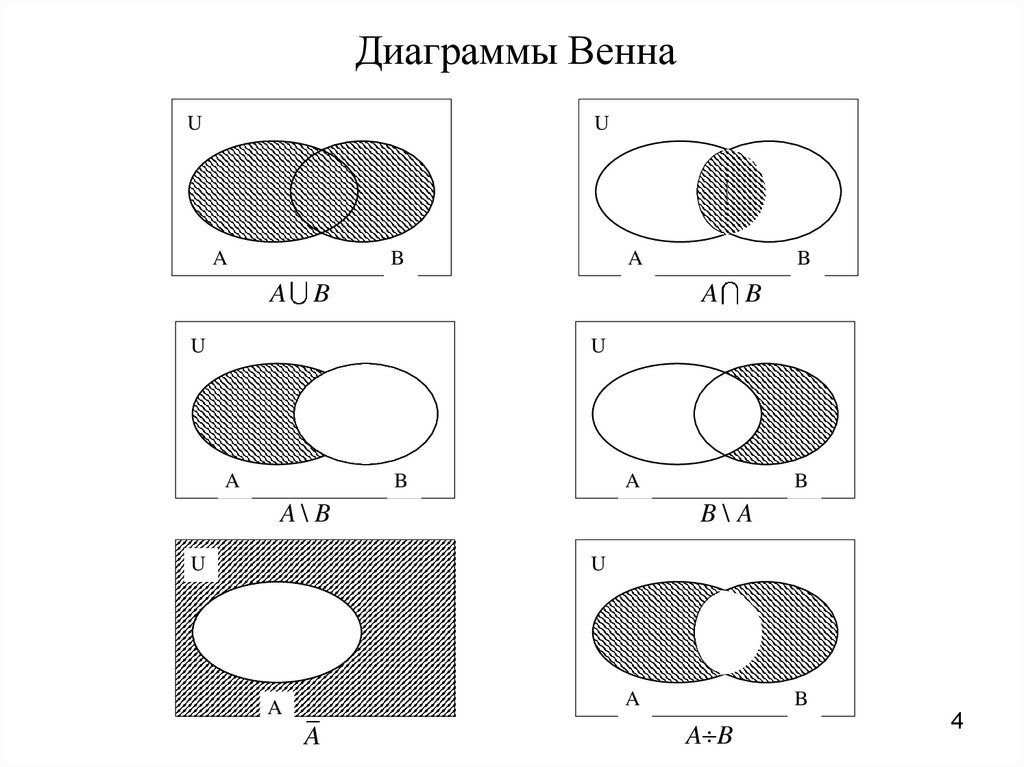
Объединением множеств A и B – A B={x|x A или x B}.
\
Пересечением множеств A и B – A B={x|x A и x B}.
Разностью множеств A и B – A\B={x | x A и x B}.
Симметрической разностью множеств A и B –
A B={x | x A и x B или x A и x B}=(A\B) (B\A).
Дополнением к множеству A – A =U\A.
1
3

4.

Диаграммы Венна
U
U
A
B
A
A
B
B
A
U
B
U
A
B
A
A\ B
U
B
B\A
U
A
A
A
B
A B
4

5.

Объединение некоторой совокупности (более двух элементов) множеств:
а)
A – объединение всех множеств,
A S
являющихся элементами множества S;
Ai – объединение множеств Ai ,
b)
i I
индекс i пробегает все значения множества I;
k
c)
i 1
Ai – объединение множеств Ai ,
индекс i пробегает все значения от 1 до k;
d)
Ai – объединение бесконечного количества множеств.
i 1
k
Аналогично определеяются:
A,
A S
Ai ,
i I
Ai ,
i 1
Ai
i 1
5

6.

Обозначения наиболее часто используемых
числовых множеств
– множество всех натуральных чисел;
– множество всех целых чисел;
– множество всех рациональных чисел;
– множество всех действительных чисел;
x x
и x 0 ,
x x
и x 0 ;
x x
и x 0 ,
x x
и x 0 ;
x x
и x 0 ,
x x
и x 0 .
6

7.

П р и м е р . Доказать, что для произвольных множеств A и B, если A B , то B A .
Пусть a B .
Тогда по определению дополнения a U \ B , где U – универсальное множество.
По определению разности множеств, из того, что a U \ B , следует, что
a U и a B .
По условию задачи известно, что A B , т.е., что все элементы множества A
есть в множестве B. Так как a B , то элемента a в множестве B нет, а следовательно, его нет и в множестве A, т.е. a A .
Итак, мы установили, что a U и a A , а значит, a A .
Аналогично доказывается обратное утверждение: если B A , то A B .
a B
df "дополнения"
a U и a B
т.к. A B
a U и a A
df "дополнения"
a A .
7

8.

Основные законы теории множеств
1. Коммутативность операций и :
а) A B=B A;
б) A B=B A
2. Ассоциативность операций и :
а) A (B C)=(A B) C;
б) A (B C)=(A B) C
3. Законы идемпотентности операций и :
а) A A=A;
4. Законы дистрибутивности:
а) A (B C)=(A B) (A С);
5. Законы поглощения:
а) A (A B)=A;
б) A A=A
б) A (B C)=(A B) (A С)
б) A (A B)=A
6. Законы де Моргана:
а) A B A B ;
б) A B A B
7. Законы пустого и универсального множеств:
A = A
A =
A A =
U
A U=U
A U= A
8. Закон двойного отрицания: A A
A A =U
U
8

9.

Теорема об единственности дополнения. Относительно заданного
универсального множества U дополнение A любого множества A U ,
единственно.
Докажем от противного. Пусть существует два множества B и C,
каждое из которых удовлетворяет требованиям дополнения множества A:
а) B
A ;
б) C
A ;
в) B
A U ;
г) C
A U .
г)
B B U B B
C
B B C
A
B
B
закон
дистрибутивности
C
A B C
B
A
а)
A B B C B C.
Аналогично исходя из условий в), б) получим:
C C U C
B
A C
B
C
A C
Итак, мы получили, что B B C и C C
B C
B.
B , а значит, в силу ком-
мутативности пересечения B C , что и требовалось доказать.
9

10.

Декартово произведение и отношение
Декартовым или прямым произведением множеств A1, A2, ... , An называется
множество
n
A1 A2 ... An= Ak ={(x1,x2,...,xn)|x1 A1, x2 A2, ... , xn An}.
k 1
Если A1=A2=...=An, то множество A1 A2 ... An =An называется n-й декартовой
степенью множества A.
По определению A0= .
Если хотя бы одно из множеств Ai пусто, то A1 A2 ... An= .
N-местным отношением (соответствием) P, или n-местным предикатом P
на множествах A1, A2, ... , An, называется некоторое подмножество прямого произведения A1 A2 ... An.
Если A1=A2=...=An=A, т.е. P An, то чаще используется термин «отношение»:
« P – n-местное отношение (предикат) на множестве A».
Если же A1 A2 ... An, то обычно используют термин «соответствие».
При n = 1 отношение P является подмножеством множества A и называется унарным (одноместным) отношением (или свойством) на множестве A.
При n = 2 отношение P называется бинарным (двухместным) отношением. 10

11.

Способы задания бинарных отношений
Аналитические
P A B, A={6,7,8}, B={5,6,7,8,9}
1. Перечислением элементов
3. (n,m)-матрицей
P={(6,5), (7,5), (7,6), (8,5), (8,6), (8,7)}
P 5 6 7 8
2. Характеристическим свойством
6 1 0 0 0
P={(a,b) | a A, b B и a>b}
7 1 1 0 0
8 1 1 1 0
Графические
4 B
3
2
1
4. Множество точек на плоскости (A и B – числовые множества)
A
1
2
3
A
4
1
b
2
c
3
a
b
f
P A B, A={1,2,3,4,5}, B={1,2,3,4},
P={(2,1), (1,2), (2,2), (3,2), (4,2), (1,3), (2,4)}.
5
B
a
c
9
0
0
0
d
5. В виде диаграммы
P A B, A={a, b, c}, B={1, 2, 3},
P={(a,2), (a,3), (b,1), (c,1)}.
6. В виде графа (A=B)
P A B, A={a, b, c, d, f},
P={(a,c), (c,a), (b,a), (b,b),(a,d)}
11

12.

Пусть P – некоторое бинарное отношение.
Область определения P
P={x|(x,y) для некоторого y}.
Область значений P
P={y|(x,y) для некоторого x}.
Обратное к P отношение
P–1={(y,x)|(x,y) }.
Композиция бинарных отношений P1 A B и P2 B C
P3= P1 P2 ={(x,y) | x A, y C и найдется z B такой, что (x,z) P1 и (z,y) P2}.
Образ множества X относительно P
P(X)={y|(x,y) для некоторого x X}.
Прообраз множества Y относительно P
P-1(Y)={x|(x,y) для некоторого y Y}.
12

13.

Пример.
Найти P , P , P 1 , P P , P 1 P , P P 1 , если для отношения
P
x, y x, y
, y делится на x
1) P .
а) P по определению P ;
б) P , так как для произвольного x
например, y = x, такой, что x, y P .
2) P .
а) P по определению P ;
б) P , так как для произвольного y
например, x = y, такой, что x, y P .
можно подобрать y,
можно подобрать x,
3) P 1 x, y x, y , x делится на y
13

14.

P
4) P P 1 2
а) P P 1
x, y x, y
2
, y делится на x
по определению;
б) x, y 2 x, y и найдется z , например, z xy ,
который делится на x и на y
x, y
и найдётся z , такой, что x, z P и z, y P 1
x, y P P 1 .
5) P 1 P 2
а) P 1 P
2
по определению;
б) x, y 2 x, y
и найдется, например, z 1 такой,
что x и y будут кратны z
x, y
и найдется z, такой, что x, z P 1 и z , y P
x, y P 1 P.
14

15.

P
x, y x, y
, y делится на x
6) P P P
а) x, y P P x, y
и нашелся z
такой, что x, z P и
x, y
и нашелся z
,
z, y P
,
такой, что z делится на x и y делится на z
и y делится на x x, y P .
x, y
б) x, y P x, y
x, y
и y делится на x
и найдется z
, например, z x , такой,
что z делится на x и y делится на z
x, y
и найдется z
такой, что x, z P и z, y P
x, y P P.
15

16.

П р и м е р . Найти относительно множества P образ множества X и
прообраз множества Y, если:
x, y x, y , y делится на x ,
X={2,3}, Y y y N , 5 y 10 ;
а) P
б) P
x, y x, y
, y x 1 ,
X x x , 4 x 9 ,
Y y y , 17 y 26 .
а) P X y y , и y делится на 2 или на 3
y y и для некоторого m
верно, что y 2m или y 3m ,
P 1 Y 1,2,3,4,5,6,7,8,9 x x , x 10
б) P X P 4,9 y y , 3 y 4 ,
P 1 Y P 1 17,26 162 ,252 x x , 162 x 252
16

17.

Специальные бинарные отношения
Отношение обладает(+), не
обладает (-) свойством:
рефлексивности
иррефлексивности
Определение
+
Если (x,x) P для всех x A
–
Если существует x A, такой, что (x,x) P
+
Если (x,x) P для всех x A
–
Если существует x A, такой, что (x,x) P
+
симметричности
–
антисимметричности
P A2, A
+
–
+
транзитивности
–
Если для всех x,y A
из того, что (x,y) P, следует, что (y,x) P
Если существуют x,y A,
такие, что (x,y) P, (y,x) P
Если для всех x,y A
из того, что (x,y) P и (y,x) P, следует x=y
Если существуют x,y A, такие, что (x,y) P, (y,x) P, x y
Если для всех x,y,z A
из того, что (x, y) P и (y, z) P, следует, что (x,z) P.
Если существуют x,y,z A,
такие, что (x, y) P, (y, z) P, (x,z) P
17

18.

транзитивность
антисимметричность
симметричность
иррефлексивность
рефлексивность
P A2, A={1, 2, 3}
1) P={(1,1), (2,2), (3,3), (1,2), (2,1)}
2) P={(1,2), (2,3), (1,3)}
3) P={(1,1), (2,3), (3,1)}
4) P={(2,1), (1,2)}
P L2, L– множество людей
6) P x, y x, y L, x моложе y
7) P x, y x, y L, x не моложе y
8) P x, y x, y L, x знает адрес y
5) P x, y x, y L, x живет в одном городе с y
18

19.

Специальные бинарные отношения
Отношение обладает(+), не
обладает (-) свойством:
+
рефлексивности
–
иррефлексивности
Если (x,x) P для всех x A
Если существует x A, такой, что (x,x) P
Если (x,x) P для всех x A
–
Если существует x A, такой, что (x,x) P
симметричности
–
+
–
+
транзитивности
–
P A2, A={1, 2, 3}
Определение
+
+
антисимметричности
P A2, A
Если для всех x,y A
из того, что (x,y) P, следует, что (y,x) P
Если существуют x,y A,
такие, что (x,y) P, (y,x) P
Если для всех x,y A
из того, что (x,y) P и (y,x) P, следует x=y
Если существуют x,y A, такие, что (x,y) P, (y,x) P, x y
Если для всех x,y,z A
из того, что (x, y) P и (y, z) P, следует, что (x,z) P.
Если существуют x,y,z A,
такие, что (x, y) P, (y, z) P, (x,z) P
1) P={(1,1), (2,2), (3,3), (1,2), (2,1)}
2) P={(1,2), (2,3), (1,3)}
19

20.

Специальные бинарные отношения
Отношение обладает(+), не
обладает (-) свойством:
+
рефлексивности
–
иррефлексивности
Если (x,x) P для всех x A
Если существует x A, такой, что (x,x) P
Если (x,x) P для всех x A
–
Если существует x A, такой, что (x,x) P
симметричности
–
+
–
+
транзитивности
–
P A2, A={1, 2, 3}
Определение
+
+
антисимметричности
P A2, A
Если для всех x,y A
из того, что (x,y) P, следует, что (y,x) P
Если существуют x,y A,
такие, что (x,y) P, (y,x) P
Если для всех x,y A
из того, что (x,y) P и (y,x) P, следует x=y
Если существуют x,y A, такие, что (x,y) P, (y,x) P, x y
Если для всех x,y,z A
из того, что (x, y) P и (y, z) P, следует, что (x,z) P.
Если существуют x,y,z A,
такие, что (x, y) P, (y, z) P, (x,z) P
3) P={(1,1), (2,3), (3,1)}
4) P={(2,1), (1,2)}
20

21.

Специальные бинарные отношения
Отношение обладает(+), не
обладает (-) свойством:
+
рефлексивности
–
иррефлексивности
Определение
Если (x,x) P для всех x A
Если существует x A, такой, что (x,x) P
+
Если (x,x) P для всех x A
–
Если существует x A, такой, что (x,x) P
+
симметричности
–
антисимметричности
P A2, A
+
–
+
транзитивности
Если для всех x,y A
из того, что (x,y) P, следует, что (y,x) P
Если существуют x,y A,
такие, что (x,y) P, (y,x) P
Если для всех x,y A
из того, что (x,y) P и (y,x) P, следует x=y
Если существуют x,y A, такие, что (x,y) P, (y,x) P, x y
Если для всех x,y,z A
из того, что (x, y) P и (y, z) P, следует, что (x,z) P.
–
P L2, L– множество людей
Если существуют x,y,z A,
такие, что (x, y) P, (y, z) P, (x,z) P
6) P x, y x, y L, x моложе y
5) P x, y x, y L, x живет в одном городе с y
21

22.

Специальные бинарные отношения
Отношение обладает(+), не
обладает (-) свойством:
+
рефлексивности
–
иррефлексивности
Определение
Если (x,x) P для всех x A
Если существует x A, такой, что (x,x) P
+
Если (x,x) P для всех x A
–
Если существует x A, такой, что (x,x) P
+
симметричности
–
антисимметричности
P A2, A
+
–
+
транзитивности
Если для всех x,y A
из того, что (x,y) P, следует, что (y,x) P
Если существуют x,y A,
такие, что (x,y) P, (y,x) P
Если для всех x,y A
из того, что (x,y) P и (y,x) P, следует x=y
Если существуют x,y A, такие, что (x,y) P, (y,x) P, x y
Если для всех x,y,z A
из того, что (x, y) P и (y, z) P, следует, что (x,z) P.
–
P L2, L– множество людей
Если существуют x,y,z A,
такие, что (x, y) P, (y, z) P, (x,z) P
x, y x, y L, x не моложе y
8) P x, y x, y L, x знает адрес y
7) P
22

23.

P A2, A
idA={(x,x)|x A} – тождественное отношение ( или диагональ)
uA=A2 – универсальное отношение (или полное отношение).
P – отношение
эквивалентности
(эквивалентность)
P – отношение
нестрогого порядка
P – отношение
строгого порядка
рефлексивно, симметрично, транзитивно
антисимметрично,
транзитивно,
рефлексивно
иррефлексивно
Отношение P эквивалентности разбивает множество A, на непересекающиеся
подмножества (классы эквивалентности):
a, b P «Элементы a и b из одного подмножества».
Элементы a A и b A сравнимы по отношению P на множестве A, если
a, b P или b, a P .
Множество A, на котором задано отношение порядка
– полностью упорядоченно, если любые два элемента множества A
сравнимы по отношению P,
– частично упорядоченно, в противном случае.
23

24.

П р и м е р . Доказать, что если отношения P и S симметричны, то симметричны
и отношения P S , P 1 .
Пусть
x, y
произвольная пара бинарного отношения P S . Тогда из
определения операции объединения следует, что
« x, y P или x, y S »:
1) если x, y P , то в силу симметричности P y, x P ,
2) если x, y S , то в силу симметричности S y, x S .
Таким образом, взяв произвольную пару x, y множества P S , мы показали, что в одном из множеств P или S, а значит, в множестве P S , будет присутствовать пара y, x , что и требовалось доказать.
x, y P
S x, y P или x, y S
df
P и S симметричны
y , x P или y , x S y , x P S .
df
x, y P
1
df P 1
y, x P
P симметрично
x, y P
df P 1
y, x P
1
.
24

25.

П р и м е р . Доказать, что для произвольного бинарного отношения P
композиция P P 1 является симметричным отношением.
df
x, y P P найдется такой z, что x, z P и z, y P
1
найдется такой z, что z, x P
1
1
df P 1
df
и y , z P y , x P P 1.
П р и м е р . Доказать, что если отношение P симметрично и антисимметрично одновременно, то оно транзитивно.
x, y P,
y, z P.
P симметрично
P антисимметрично
x, y P, y, x P,
y, z P, z, y P.
x, y P, y, x P, x y
x, z P .
y, z P, z, y P, y z.
25

26.

Функции
f : A1 A2 ... An B
Бинарное
отношение
называется
n-местной
функцией
(функциональным
отношением,
однозначным
отношением),
действующей
из
A A1 A2 ... An в B, если f A , f B и для всех x x1 , x2 ,..., xn , из того, что x, y1 f и
x, y2 f , следует
y1 y2 .
Если f – функция, то вместо
x , x ,..., x , y f
1
2
n
принято писать y f x1 , x2 ,..., xn .
Если f A , то f – всюду определенная функция,
иначе f – частично определенная функция.
Функция f называется
– инъекцией, если для всех x1, x2 из того, что x1 x2 , следует, что f x1 f x2 ;
– сюръекцией, если f B .
– биекцией (взаимно однозначным соответствием между A и B), если она является инъекцией и сюръекцией одновременно.
«f есть отображение A в B», если функция f : A B всюду определена;
«f есть отображение A на B», если функция f : A B всюду определена и сюръекция
Отображение f : A A часто называют преобразованием множества A.
Функциональное отображение f : A A часто называют перестановкой на множестве27
A.

27.

1, если x A,
Характеристическая функция множества A: A x
0, если x A.
Функции f и g равны, если:
1) совпадают их области определения;
2) для любого элемента a из области определения f a g a .
Функция f 1 : B A называется обратной функцией к функции f : A B .
Функция h : A C называется композицией функций f : A B и g : B C , если
h x f g g f x , где x A .
Суперпозицией
функций
f1 , f 2 ,..., f n
называется
функция,
полученная
из
f1 , f 2 ,..., f n некоторой подстановкой их друг в друга и переименованием аргументов.
Выражение, описывающее эту суперпозицию, называется формулой суперпозиции.
28

28.

Операции
Операция – функция, все аргументы которой принадлежат одному и тому же
множеству. Если и значения операции принадлежат этому же множеству, то
говорят, что множество замкнуто относительно операции.
n-местная функция : An A называется n-арной операцией на множестве A
(n
1 –унарная операция, n 2 – бинарная операция.
Свойства бинарных операций
1) – коммутативна, если для любых a, b: a b b a .
2) – ассоциативна, если для любых a, b, c:
a b
c a b c .
3) – дистрибутивна слева относительно операции , если для любых a, b, c:
a b c a b a c ,
– дистрибутивна справа относительно операции , если для любых a, b, c:
a b
c a c b c ;
4) – идемпотентна, если для любых a:
a a a.
29