Похожие презентации:
Теория множеств и бинарные отношения
1.
Модуль 1Теория множеств и
бинарные отношения
Занятие 1.3. Функции и
операции
2020 г.
2.
Содержание1.
2.
3.
4.
5.
6.
7.
Связи между понятиями
Бинарное отношение
Определение функции
Виды функций
Операции
Построение функций
Свойства бинарных отношений
3.
Связи между понятиямиБинарное
отношение
Декартово
произведение
Функция
Операция
4.
.Бинарное отношение
Бинарным отношением Т(М)
на множестве М называется
подмножество M 2 M M ,
T(M) M
2
Инфиксная форма записи
бинарного отношения
a T b ={( a, b ) /( a, b ) T M M }
5.
Виды бинарныхотношений
Обратное отношение
1
R {( x, y ) /( y, x ) R}
Дополнительное отношение
R {( x , y ) /( x , y ) R}
6.
Виды бинарныхотношений
Тождественное отношение
U {( x , x ) / x M }
Универсальное отношение
I {( x , y ) / x M _ и _ y M }
7.
Обратное отношениеОбратное отношение
1
R {( x, y ) /( y, x ) R}
8.
Дополнительноеотношение
Дополнительное отношение
R {( x , y ) /( x , y ) R}
9.
Тождественноеотношение
Тождественное отношение
U {( x , x ) / x M }
10.
Универсальноеотношение
Универсальное отношение
I {( x , y ) / x M _ и _ y M }
11.
ФункцияF X Y
называется функцией, если
для каждого элемента х найдется не
более одного элемента у такого, что
(x, y) F
, т.е. выполняется свойство
однозначности полученного результата
Множество X - область определения
функции, и множество Y - область
значений функции
Х и У могут не иметь общих элементов
12.
Построение функцииДаны множества X={a, b, c, d} и Y={x, y, z}.
Построить функцию F: X=> Y таким образом,
что ( a , x ) F
a
X={a, b, c, d}
b
c
d
x
y
z
Y={x, y, z}
13.
ИнъекцияФункция F: X →Y называется
инъективной (инъекцией или
вложением), если она переводит
разные элементы Х в разные У,
то есть
x X _ и _ z X , x z F ( x ) F ( z )
14.
Построение инъекцииДаны множества X={x1, x2, x3}
Y={y1, y2}. Построить инъекцию
F: X →Y
x1
X={x1, x2, x3}
y1
Y={y1, y2}
x2
x3
y2
15.
СюръекцияФункция F: X → Y называется
сюръективной (сюръекцией или
наложением), если множество ее
значений есть все Y, т.е.
y Y _ x X , _ y F ( x )
16.
Построение сюръекцииДаны множества X={x1, x2, x3} и
Y={y1, y2}. Построить сюрьекцию
F: X →Y
x1
X={x1, x2, x3}
y1
Y={y1, y2}
x2
x3
y2
17.
БиекцияФункция F: X →Y называется
биекцией или взаимно
однозначным соответствием,
если она одновременно является
инъекцией и сюръекцией
(вложением и наложением), т.е.
x X _ и _ z X , x z F ( x ) F ( z )
y Y _ x X , _ y F ( x )
18.
Построение биекцииДаны множества X={x1, x2, x3} и Y={y1,
y2}. Построить биекцию F: X →Y
x1
X={x1, x2, x3} x2
x3
y1
Y={y1, y2, y3}
y2
y3
19.
ОперацияЧастным случаем функции является
операция О
В этом случае область значения Х и
область определения У совпадают,
т.е
O M , x M ! y ,( x , y ) O
2
20.
ОперацияДано множество X={x1, x2, x3}.
Построить операцию F: X →X
x1
X={x1, x2, x3}
x1
X={x1, x2, x3}
x2
x3
x2
x3
21.
Решение задачДано множество натуральных чисел N. Укажите,
какие из арифметических действий (сложение,
вычитание, умножение, деление) всегда
выполнимы на этом множестве?
22.
Решение задачДано множество натуральных чисел N. Укажите,
какие из арифметических действий (сложение,
вычитание, умножение, деление) всегда
выполнимы на этом множестве?
Решение
сложение
умножение
Результат операций должен принадлежать
множеству натуральных чисел N
23.
Решение задачНа множестве натуральных чисел задана О
операция. Какой может быть эта операция?
а) a О b = ab;
б) a О b = a + b;
в) a О b = a – b.
24.
Решение задачНа множестве натуральных чисел задана О
операция. Какой может быть эта операция?
а) a О b = ab;
б) a О b = a + b;
в) a О b = a – b.
Решение
возведение в степень
сложение
Результат операций должен принадлежать
множеству натуральных чисел N
25.
Решение задачНа множестве рациональных чисел задана О
операция . Какой может быть эта операция?
а) a О b = a ^ b;
б) a О b = a + b;
в) a О b = a – b;
26.
Решение задачНа множестве рациональных чисел задана О
операция . Какой может быть эта операция?
а) a О b = a ^ b;
б) a О b = a + b;
в) a О b = a – b;
Решение
сложение
вычитание
Результат операций должен принадлежать
множеству рациональных чисел N
27.
РефлексивностьБинарное отношение T(M),
называется рефлексивным тогда
и только тогда, когда для каждого
M
элемента пара (х, х) принадлежит
этому бинарному отношению, т.е.
x M _ ( x , x ) T ( M )
M ,T
28.
ИррефлексивностьБинарное отношение T(M)
называется иррефлексивным
тогда и только тогда, когда для
каждого элемента пара (х, х) не
принадлежит этому бинарному
отношению, т.е.
x M _( x , x ) T ( M )
M ,T
29.
НерефлексивностьЕсли бинарное отношение T(M)
не обладает ни свойством
рефлексивности, ни свойством
иррефлексивности, то оно
является нерефлексивным
30.
Примерырефлексивности
а
b
а
b
а
b
c
d
c
d
c
d
рефлексивно
иррефлексивно
нерефлексивно
31.
СимметричностьБинарное отношение T(M) называется
симметричным тогда и только тогда,
когда для каждой пары различных
элементов (х, у) и x≠y из Т, обратная
пара (у, х) также принадлежит этому
бинарному отношению, т.е.
( x , y ) T ( M ) _ ( y , x ) T ( M )
M 1 ,T
32.
АнтисимметричностьБинарное отношение T(M) называется
антисимметричным тогда и только
тогда, когда для каждой пары различных
элементов (х, у) и x≠y из Т, пара (у, х) не
принадлежит этому бинарному
отношению, т.е.
( x , y ) T ( M ) _( y , x ) T ( M )
M 1 ,T
33.
Другое определениеантисимметричности
Бинарное отношение T(M) называется
антисимметричным тогда и только
тогда, когда из того, что (x, y) T(M)
и
(y, x) T(M) следует, что
x y
34.
НесимметричностьЕсли бинарное отношение T(M)
не обладает ни свойством
симметричности, ни свойством
антисимметричности, то оно
является несимметричным
35.
Примерысимметричности
а
b
а
b
а
b
c
d
c
d
c
d
симметрично
несимметрично
антисимметрично
36.
ТранзитивностьБинарное отношение T(M) называется
транзитивным тогда и только тогда,
когда для каждых двух пар различных
элементов (х,у) и (у, z), принадлежащих
бинарному отношению, пара (x, z) также
принадлежит этому бинарному
отношению, т.е.
( x , y ),( y , z ) T ( M ) _ ( x , z ) T ( M )
M 2, T 2
37.
ИнтранзитивностьБинарное отношение T(M) называется
интранзитивным тогда и только тогда,
когда для каждых двух пар различных
элементов (х, у) и (у,z),
принадлежащих бинарному отношению
, пара (x, z) не принадлежит этому
бинарному отношению, т.е.
( x , y ),( y , z ) T ( M ) _ ( x , z ) T ( M )
M 2, T 2
38.
НетранзитивностьЕсли бинарное отношение T(M)
не обладает ни свойством
транзитивности, ни свойством
интранзитивности, то оно
является нетранзитивным
39.
Примерытранзитивности
а
b
а
b
а
b
c
d
c
d
c
d
транзитивно
интранзитивно
нетранзитивно
40.
Определение свойствбинарных отношений
b
f
e
a
c
d
41.
Определение свойствбинарных отношений
b
f
e
a
c
d
• нерефлексивность (часть вершин имеет петли, часть –нет)
• несимметричность (есть симметричные и
антисимметричные дуги)
• интранзитивность (бинарное отношение обладает
несколькими путями длины 2, но нет ни
одного транзитивного замыкания)
42.
Определение свойствбинарных отношений
b
f
e
a
c
d
43.
Определение свойствбинарных отношений
b
f
e
a
c
d
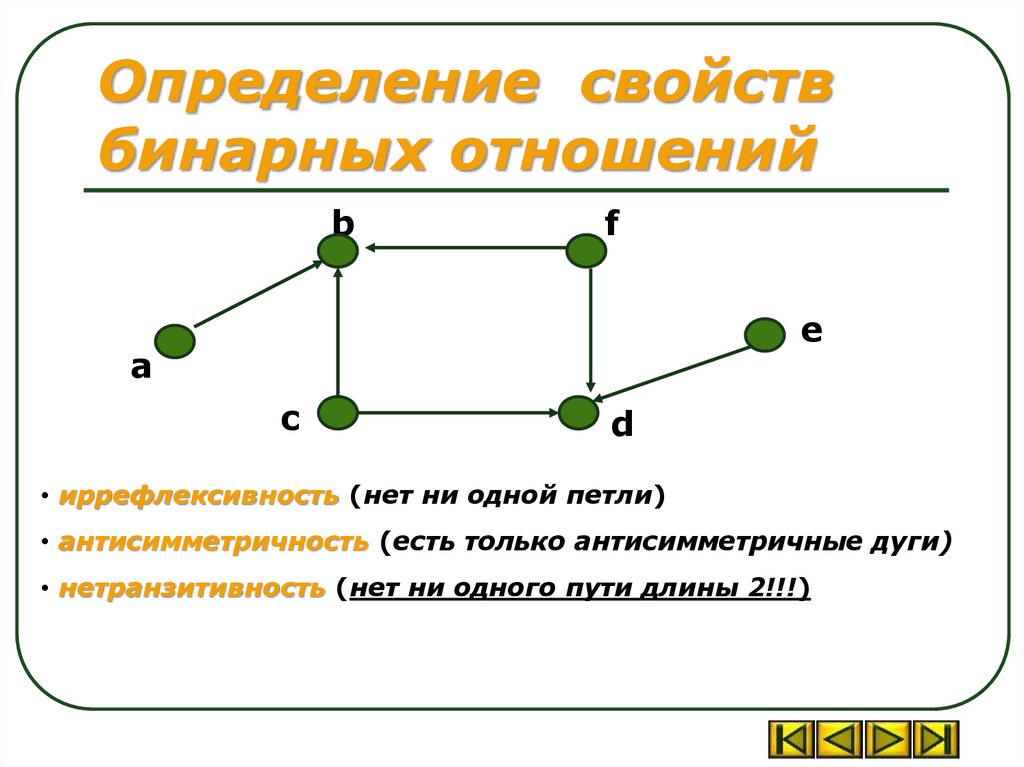
• иррефлексивность (нет ни одной петли)
• антисимметричность (есть только антисимметричные дуги)
• нетранзитивность (нет ни одного пути длины 2!!!)
44.
Определение свойствбинарных отношений
b
f
e
a
c
d
45.
Определение свойствбинарных отношений
b
f
e
a
c
d
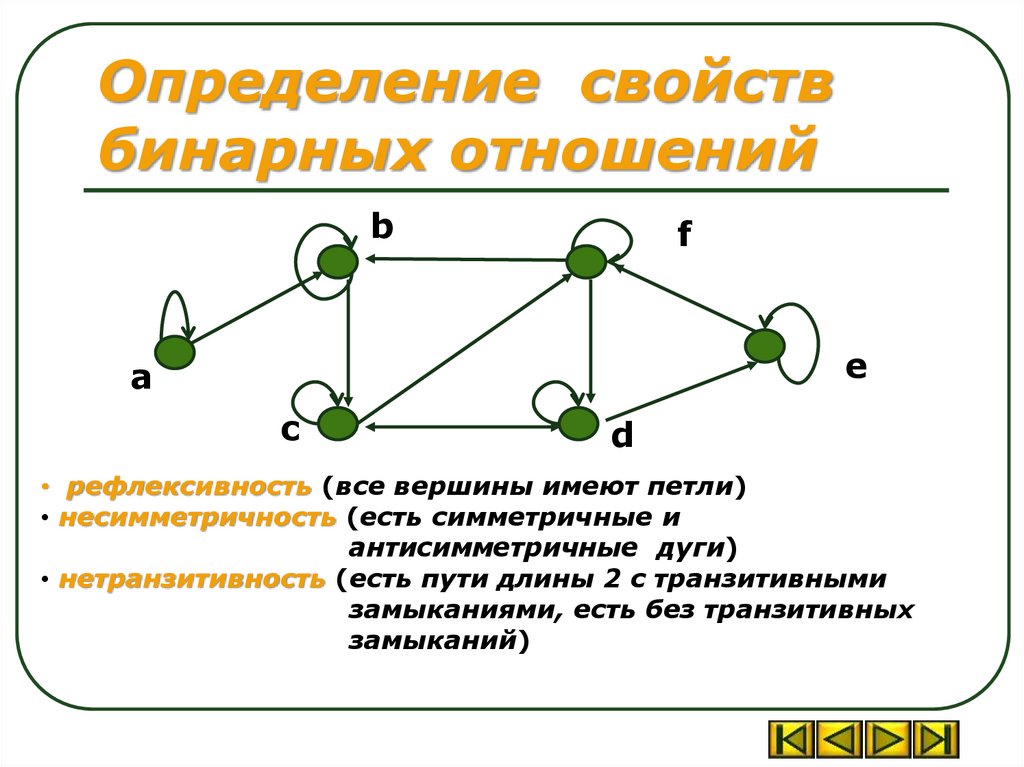
• рефлексивность (все вершины имеют петли)
• несимметричность (есть симметричные и
антисимметричные дуги)
• нетранзитивность (есть пути длины 2 с транзитивными
замыканиями, есть без транзитивных
замыканий)
46.
Определение свойствбинарных отношений
На множестве натуральных чисел задано
отношение равенства (а=b). Какими свойствами
(рефлексивность, симметричность,
транзитивность) обладает это отношение?
1
2
...
n
...
• рефлексивность (число равно a самому себе, a=a )
• несимметричность (нет ни одной дуги между различными
элементами a и b!!! )
• нетранзитивность (нет ни одного пути длины 2!!!)
47.
Определение свойствбинарных отношений
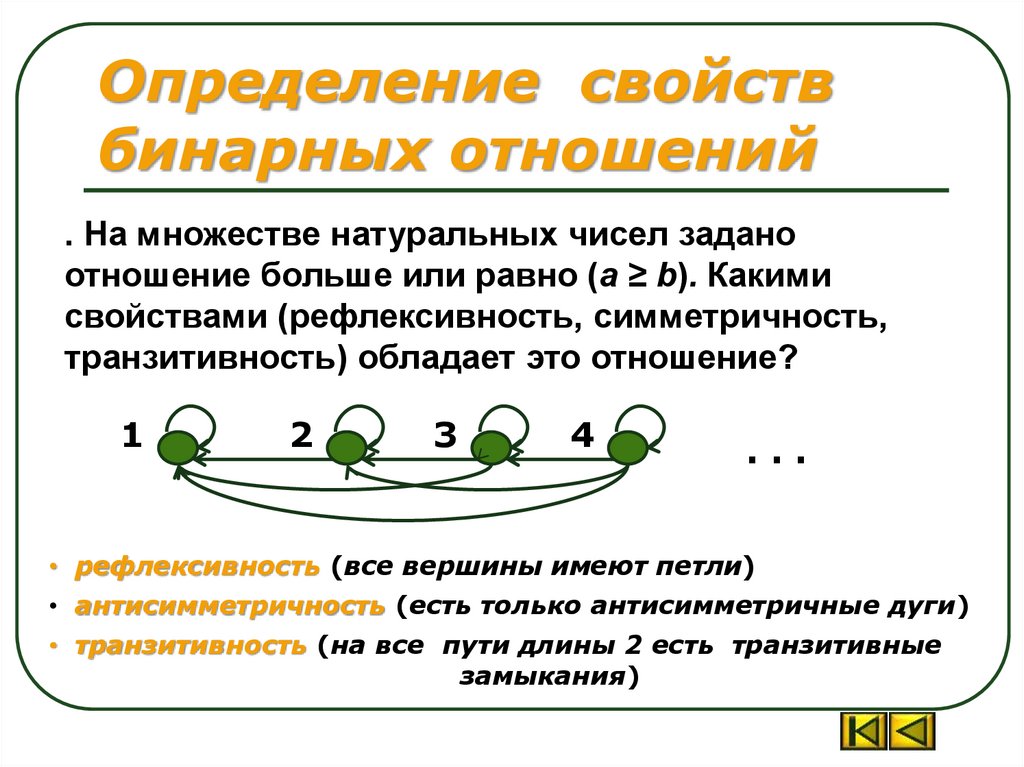
. На множестве натуральных чисел задано
отношение больше или равно (а ≥ b). Какими
свойствами (рефлексивность, симметричность,
транзитивность) обладает это отношение?
1
2
3
4
...
• рефлексивность (все вершины имеют петли)
• антисимметричность (есть только антисимметричные дуги)
• транзитивность (на все пути длины 2 есть транзитивные
замыкания)












































 Математика
Математика








