Динамика. Первый закон Ньютона

1. Динамика

2. Первый закон Ньютона

Существуют такие системы отсчета,
относительно которых тело сохраняет
состояние покоя или равномерного и
прямолинейного движения до тех пор, пока
воздействие со стороны других тел не
заставит его изменить это состояние.
Свойство тел сохранять состояние покоя
или равномерного и прямолинейного
движения при отсутствии воздействия со
стороны других тел называется инерцией.

3. Инерциальные системы отсчета

Системы отсчета, относительно которых
выполняется 1 закон Ньютона, называются
инерциальными. Инерциальной системой
отсчета (ИСО)является такая система, которая
либо покоится, либо движется равномерно и
прямолинейно относительно какой-то другой
инерциальной системы отсчета.
Системы отсчета, в которых первый закон
Ньютона не выполняется, называются
неинерциальными.

4. Сила, масса, импульс

Сила - это мера воздействия одного тела на другое в
результате которого тела приобретают ускорения,
или деформируются, или имеет место то и другое
одновременно.
Сила величина векторная.
О наличии и действии сил мы можем судить:
1. по их динамическому проявлению, т.е. по тем
ускорениям,
которые
они
сообщают
взаимодействующим телам;
2. по статическому проявлению сил - по деформациям,
которые возникают во взаимодействующих телах.

5.

Масса – мера инертности тела, а также
мера его гравитационных свойств.
m = m0 /
m – масса движущегося тела
m0 – масса покоящегося тела
1 2 с2
При
υ<< с
m0 = m
Импульс
–
количественная
мера
механического движения, которое может
быть передано от одной материальной точки
другой.
2
~с
υ <<с
р = m0 /
р m
1-
c2

6. Второй закон Ньютона

Скорость изменения импульса материальной
точки
равна
результирующей
всех
сил,
действующих на эту точку:
d
m
F
dt
Fdt d ( m )
Fdt - элементарный импульс силы
F∆t = m∆υ ,
F∆t = ∆р
Импульс силы за время её действия ∆t равен
изменению импульса материальной точки за это же
время.

7. Второй закон Ньютона (продолжение)

При
m=const
d
F m
ma
dt
F
a
m
Ускорение, приобретаемое материальной точкой,
пропорционально
вызывающей
его
силе,
совпадает с ней по направлению и обратно
пропорционально массе материальной точки
(тела).

8. Третий закон Ньютона:

Силы взаимодействия двух материальных
точек равны по модулю, противоположны
по направлению и направлены вдоль линии,
соединяющей эти точки:
F12 F21
1
F12
F21
2

9. Механическая система

Совокупность взаимодействующих между
собой тел образует механическую систему.
Силы,
действующие
между
телами,
образующими
систему,
называются
внутренними силами.
Силы, действующие на тела системы, со
стороны тел, не входящих в данную систему,
называются внешними силами.

10. Пример

F2
F1
f12
1
f21
f13
2
f23
f32
f31
3
F3
fik – внутренние силы, Fi – результирующие внешних
сил

11.

Рассмотрим систему n материальных точек с массами m1,m2, m3,…,
mn.
r , r , r ,..., r .
1 , 2 ,момент
, nвремени
Их радиус-векторы в некоторый
Их мгновенные скорости
1
Центром масс ( или центром
инерции) системы материальных
точек, называется точка, радиус
вектор которой
определяется
выражением:
mi ri
n
rC
i 1
n
mi
1
М
mi ri
n
i 1
i 1
M –масса всей системы
2
3
n
mi
m1
mk ri
r1
mn
rk
●O
rn

12. Скоростью центра масс называется величина, определяемая выражением:

n
mi i
1
i 1
C
mi М
n
m
i 1
i i
i
n
М c mi i
n
m
i 1
i 1
- полный (суммарный) импульс механической системы
Суммарный импульс механической системы равен
импульсу её центра масс.
i i

13. Движение центра масс

M c mi i
Взяв производную по времени от обеих частей равенства,
получим
d ( M с ) d ( mi i)
F
dt
dt
(1)
(1)
–
2-ой
закон
Ньютона
для
системы
материальных
точек
F - результирующая всех внешних сил, действующих на
систему.
Сумма внутренних сил по 3-ему закону Ньютона равна 0:
i
k
f i ,k = 0

14. Закон сохранения импульса

По II закону Ньютона:
d ( M c) d ( mi i)
F
dt
dt
Система называется изолированной, если результирующая
внешних сил, действующих на систему равна нулю: F =0, тогда:
n
mi i const
i 1
(2)
В изолированной системе материальных тел суммарный импульс
системы есть величина постоянная.
(2) – закон сохранения импульса.
d mi i Fdt
n
При наличии внешних сил:
i 1

15. Энергия и работа

Энергия - универсальная количественная
мера различных форм движения и взаимодействия.
Она учитывает возможность перехода движения из
одной формы в другую.
Энергия – функция состояния, т.е. в данном состоянии
она принимает одно вполне определённое значение,
независимо от того, как система пришла в это состояние
Работа – одна из форм передачи механического
движения от одного тела к другому.
Работа–функция процесса. Она зависит от того, каким
способом система переходит из одного состояния в
другое.
При переходе из одного состояния в другое совершаемая
работа численно равна изменению энергии

16. Работа переменной силы

Элементарной работой силы F на перемещении dr
называется скалярная величина
δA= ( F,dr ) = Fdr.cos = FdS.cos = FS dS,
где dS = |dr | - элементарный путь;
- угол между направлениями элементарного
перемещения dr и силы F,
Fs - проекция силы на направление перемещения.
Полная работа на пути S:
A = ∫ FS dS
(S)

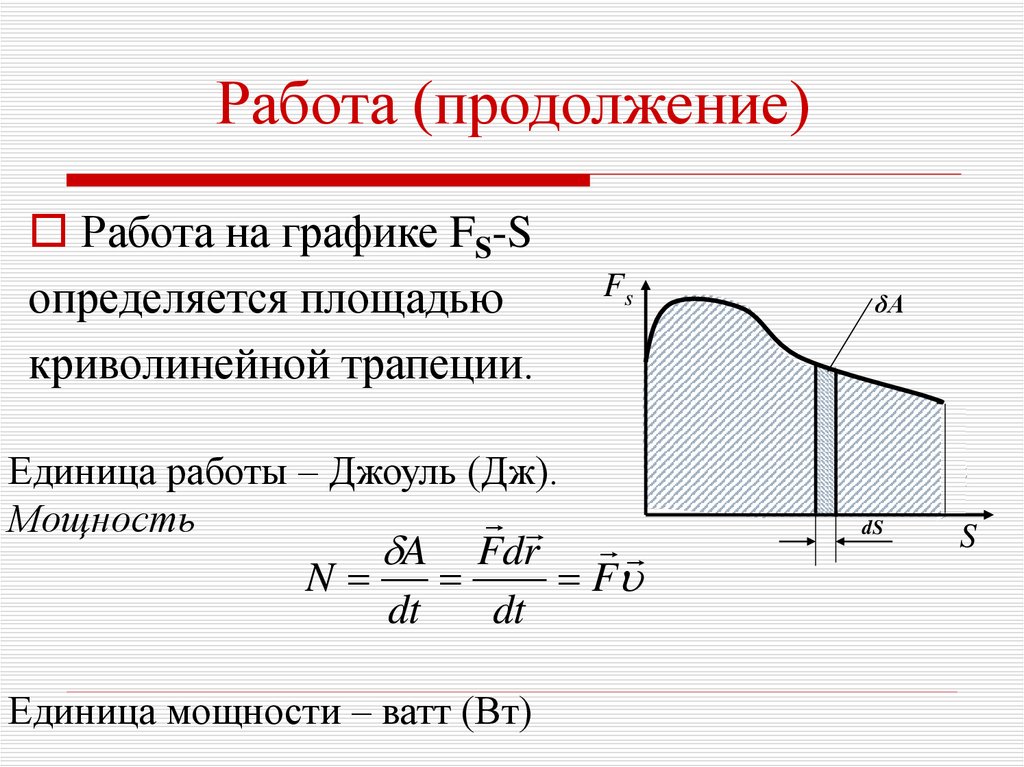
17. Работа (продолжение)

Работа на графике FS-S
определяется площадью
криволинейной трапеции.
Fs
Единица работы – Джоуль (Дж).
Мощность
A Fdr
N
F
dt
dt
Единица мощности – ватт (Вт)
δΑ
dS
S

18. Кинетическая энергия

Механическая энергия
В механике различают два вида энергии :
кинетическую и потенциальную.
Кинетическая энергия
Кинетической
называется
энергия
движущегося тела, зависящая от его скорости.
Она измеряется работой, которую может
совершить тело при торможении до полной
0
остановки:
0
m 2
A madr m d
Wк = mυ2/ 2
2

19. Консервативные и диссипативные силы

□
Силы, работа которых не зависит от формы пути, а зависит
лишь от начального и конечного положения системы,
называются консервативными или потенциальными.
□
А1а2 = А1в2
а
1
Системы, в которых действуют только
консервативные силы, называются
консервативными
или потенциальными.
в
Силы, работа которых зависит от того, как система
переходит из одного состояния в другое, называются
диссипативными .
2

20.

Рассмотрим перемещение материальной точки
в консервативном поле.
А1а2 = А1в2
А1а2 =-А2в1
1
1
а
а
в
в
2
2
А1а2 + А2в1= 0
Работа консервативных сил по замкнутому
контуру равна нулю.
( F , dl ) 0

21. Потенциальная энергия

Если система консервативная, то её можно охарактеризовать
потенциальной энергией.
Потенциальная энергия - это энергия взаимодействия
тел, определяемая их взаимным расположением и
характером сил между ними.
Потенциальная энергия измеряется работой по
переводу системы тел из данного взаимного
расположения в другое, потенциальная энергия
которого условно принята за ноль.

22. Потенциальная энергия в частных случаях

□ Если в потенциальном поле система переходит из состояния
1 в состояние 2, совершаемая при этом работа может быть
выражена через убыль потенциальной энергии.
А01 + А12 + А20 = 0
-Wn1 + A12 + Wn2 = 0
1
А12 = Wn1 - Wn2 = - ∆Wn
Сравнить: А12 = ∆Wк = Wк2 - Wк1
2
О
□ Потенциальная энергия в частных случаях
1) Потенциальная энергия в поле центральных сил:
1
Wn m M
r
2) Потенциальная энергия в поле силы тяжести:
Wn = mgh
3) Потенциальная энергия упруго деформированного тела:
W n = k x2 / 2

23. Закон сохранения механической энергии

В консервативном поле работа равна:
А12 = Wn1 –Wn2 = - ∆Wn ,
или:
А12 = Wк2 –Wк12 = ∆Wк
Wn1 –Wn2 = Wк2 –Wк1
Wn1 + Wк1 = Wк2 –Wn2
W1 = W2
В консервативной системе полная механическая энергия есть
величина постоянная.
В неконсервативной системе изменение полной механической
энергии при переходе из одного состояния в другое равно
работе, совершенной при этом внешними неконсервативными
силами.