Похожие презентации:
Принцип относительности в классической механике. Преобразования Галилея. Силы инерции
1.
ЛЕКЦИЯ № 4Принцип относительности в
классической механике.
Преобразования Галилея.
Силы инерции.
200
1
2.
ВОПРОСЫ11. Принцип относительности в
механике. Инерциальные системы
отсчёта. Преобразования Галилея.
12. Неинерциальные системы
отсчёта. Сила инерции.
13. Силы инерции во вращающихся
неинерциальных системах и
системах. Принцип эквивалентности
масс.
200
2
3.
Вопрос № 11.Принцип относительности в
механике.
Преобразования Галилея.
Инерциальные системы отсчёта.
200
3
4.
Инерциальные системыРассмотрим две системы отсчёта,
одна покоится (K), другая (K/)
движется относительно другой со
скоростью V0.
200
4
5.
2005
6.
Запишем связь между координатами(x, y, z) и (x/, y/, z/) точки «P» в
системах (K) и (K/).
Полагаем, что время в системах
одинаково: t = t/,
в начальный момент t = 0, x = x/.
200
6
7.
Получаем четыре уравненияx x v0t
y y
z z
t t
это преобразование Галилея,
используем его если V0 << c, иначе
надо использовать преобразование
Лоренца.
200
7
8.
Дифференцируем по времени:x x v0
y y
z z
200
8
9.
Или в следующем виде(напоминаем, что только для
выбранной схемы, рисунка)
vx v x v0
v y v y
vz v z
200
9
10.
Перейдём к векторамv v v0
Дифференцируем
v v a a
или для уравнения движения
ma ma F F
200
10
11.
Уравнения динамики не изменяютсяпри переходе от одной
инерциальной системы отсчёта к
другой, то есть они инвариантны.
Сила и ускорение инвариантны
(неизменны) относительно
преобразования Галилея.
200
11
12.
Итак, все инерциальные системыотсчёта инвариантны: Уравнения
движения выглядят одинаково
(дифференциальные уравнения), но
движения разные, так как разные
начальные условия (V0, r0).
200
12
13.
20013
14.
12. Неинерциальные системыотсчёта. Сила инерции.
200
14
15.
Неинерциальные системыРассмотрим две системы отсчёта,
одна инерциальная, вторая –
неинерциальная, Имеется некоторое
тело, которое движется с ускорением
ai относительно инерциальной
системы, an – относительно
неинерциальной системы.
200
15
16.
Разность ускорений тела винерциальной и неинерциальной
системах отсчёта
(для поступательного
движения)
ai an a
a – одинаково во всех точках
пространства неинерциальной
системы (a = const) и представляет
собой ускорение неинерциальной
системы отсчёта.
200
16
17.
Через 2-й закон Ньютона представимускорения.
Инерциальная система:
F
ai
m
Неинерциальная система:
F
an ai a a
m
m – масса тела.
200
17
18.
Отсюда, при F = 0 тело будетдвигаться, в неинерциальной
системе отсчёта с ускорением –a, как
если бы была сила –ma.
Введём силу инерции
Fi m ai an ma
2-й закон Ньютона в неинерциальной
системе отсчёта
man F Fi
200
18
19.
Пример: платформа с грузом(a = 0)
T
mg
200
19
20.
Платформа с грузом, наблюдательстоит рядом, ma T mg
T
ma
mg
.
.
a
200
20
21.
Платформа с грузом, наблюдательна платформе, mai T mg 0
Fi ma i
T
mg
a
200
21
22.
Все силы в физике обусловленывзаимодействием тел, то есть одно
тело действует на другое, и силы
зависят от вида взаимодействия.
Силы инерции обусловлены
свойствами системы отсчёта, в
которой рассматриваются
механические явления. В этом
смысле их можно назвать
фиктивными силами.
200
22
23.
20023
24.
13. Силы инерции во вращающихсянеинерциальных системах и
системах. Принцип эквивалентности
масс.
200
24
25.
Рассмотрим движение тела поокружности.
В инерциальной системе тело
удерживается на окружности
центростремительной силой.
В качестве центростремительной
силы могут быть следующие силы:
центростремительная сила, сила
натяжения, сила гравитационного
взаимодействия, электромагнитное
взаимодействие.
200
25
26.
ωʋ
Fцб
Fцс
143
R
26
27.
Если наблюдать из инерционнойсистемы отсчёта (наблюдатель
находится рядом, не двигается), то
необходимо использовать силу
центростремительную Fцс, которая
направлена к центру окружности и
изменяет направление движения
(модуль скорости не изменяется).
2
Fцс maцс mω R
200
27
28.
Если наблюдать из неинерционнойсистемы отсчёта (наблюдатель
двигается по окружности радиусом R
с угловой скоростью ω), то для
описания состояния вращающегося
тела необходимо ввести силу
инерции – центробежную силу Fцб,
которая будет противодействовать
силе центростремительной.
2
Fi Fцб mω R Fцс
200
28
29.
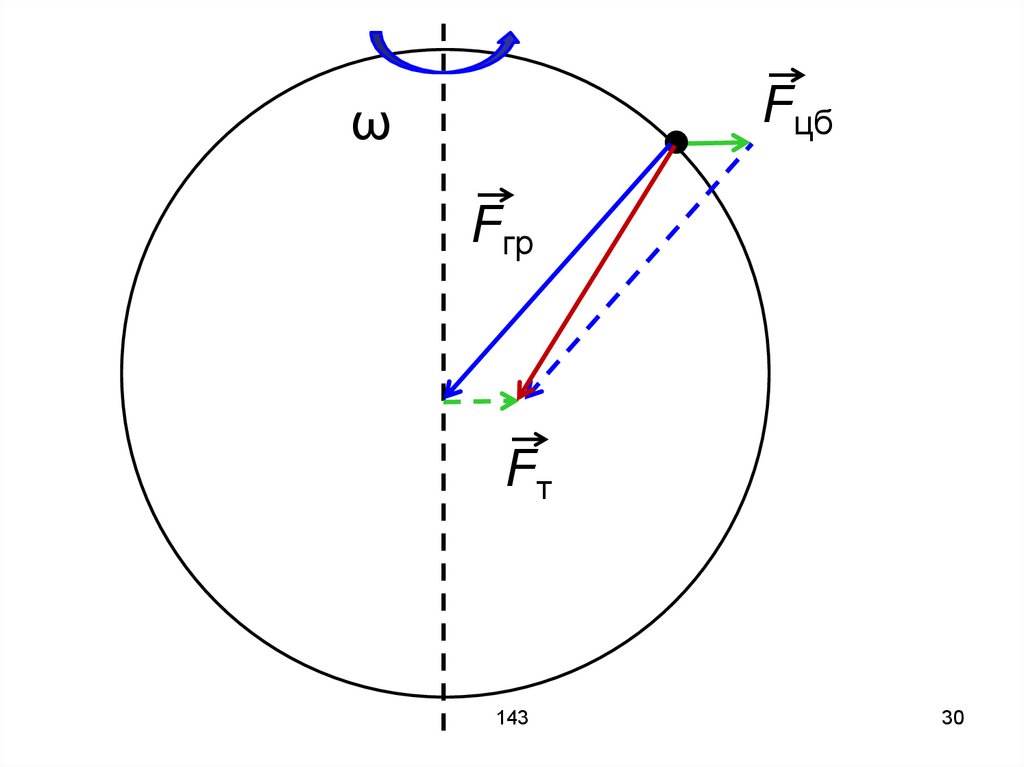
Влияние центробежной силы на силутяжести.
Сила гравитационного
взаимодействия притягивает тела на
поверхности Земли к центру Земли.
Центробежная сила направлена от
оси вращения.
Векторная сумма этих двух сил есть
сила тяжести.
200
29
30.
Fцбω
Fгр
Fт
143
30
31.
Центробежная сила на экваторе засчёт вращения Земли вокруг своей
оси:
aцб = 3,4 см/с2.
Центробежная сила за счёт
вращения Земли вокруг Солнца:
aцб = 0,6 см/с2.
200
31
32.
При движении тела относительновращающейся системы отсчёта,
кроме центробежной силы инерции,
появляется ещё одна сила,
называемая силой Кориолиса или
кориолисовой силой инерции.
FК 2m отн ω
Рассмотри случай, когда ʋотн ןω и
ʋотн II R: Fк = 2mʋотнω.
200
32
33.
20033
34.
20034
35.
Если ʋотн II ω и ʋотн ןR: Fк = 0.При движении параллельно оси
вращения, силы Кориолиса нет.
Если ʋотн ןω и ʋотн II R: Fк II Fцб.
При движении по параллелям на
запад или восток, сила Кориолиса
будет уменьшать или увеличивать
центробежную силу, соответственно.
200
35
36.
Принцип эквивалентности масс.Все физические явления в
гравитационном поле происходят
совершенно так же, как и в поле сил
инерции, если напряженности обоих
полей совпадают в соответствующих
точках пространства, а начальные
условия одинаковы для всех тел
изолированной системы.
200
36
37.
(Или) масса гравитационнаяравняется массе инерционной
F
mi
a
2
FR
mg
GM
200
37
38.
Пустили фотон с некоторой частотойν сверху вниз.
Энергия и масса фотона:
Eф = mc2, m = h ν /c2.
На высоте H (в опыте было H = 20м)
hν
hν mgH hν 2 gH
c
внизу:
hν
hν hν 2 gH
c
200
38
39.
Изменение частоты:gHν
ν 2
c
что и было зафиксировано. Точность
измерений была:
ν
15
2 10
ν
200
39
40.
20040
41.
ЛЕКЦИЯ № 5Элементы релятивистской механики
200
41
42.
ВОПРОСЫ14. Предпосылки появления
специальной теории
относительности (СТО).
15. Преобразования Лоренца.
Следствия из преобразований
Лоренца. Причинно-следственная
связь в СТО.
16. Закон сложения скоростей в СТО.
Релятивистский импульс.
200
42
43.
14. Предпосылки появленияспециальной теории
относительности (СТО).
200
43
44.
Классическая физика рассматриваетдвижение макротел с медленными
скоростями.
Описание взаимодействия тел с
помощью потенциальной энергии
предполагает мгновенное
распространение.
Причем скорость этого
распространения может быть сколь
угодно большой.
200
44
45.
Однако это противоречитэкспериментальным данным,
которые появились к концу XIX века.
По Эйнштейну существует
максимальная конечная скорость
распространения взаимодействий –
скорость света в вакууме с 3 108
м/с.
200
45
46.
В связи с механическим принципомотносительности Галилея возникает
вопрос:
равноправны ли все инерциальные
системы отсчета при рассмотрении
тепловых, электрических, магнитных,
световых и других физических
явлений, кроме механических?
200
46
47.
Как показал, Эйнштейн принципотносительности распространяется
на любые физические явления, а не
только механические.
200
47
48.
Позднее им была созданаспециальная теория
относительности (СТО) для
движения тел и частиц со
скоростями ʋ, близкими к скорости
света в вакууме (1905г.). В этой
теории предполагается, как и в
классической физике, что
пространство изотропное и
однородное и время однородное.
200
48
49.
Позднее Эйнштейн создал общуютеорию относительности (1916г.),
которая учитывает большие
гравитационные поля.
Но рассмотрим только специальную
теорию, без гравитационных полей.
200
49
50.
1-й постулат (релятивистскийпринцип относительности):
в любых инерциальных системах
отсчета все физические явления при
одних и тех же условиях протекают
одинаково, т. е. никакими
физическими опытами невозможно
установить движется данная
инерциальная система отсчёта
равномерно и прямолинейно или
покоится.
200
50
51.
Следовательно, все физическиезаконы инвариантны (независимы)
по отношению к выбору
инерциальной системы отсчета.
200
51
52.
2-й постулат (принципинвариантности скорости света в
вакууме):
Скорость света в вакууме не
зависит от вида движения источника
света, приемника и не зависит от
направления в пространстве.
200
52
53.
Эти принципы приводят к тому, чтособытия одновременные в
классической механике в
релятивистской становятся
относительными.
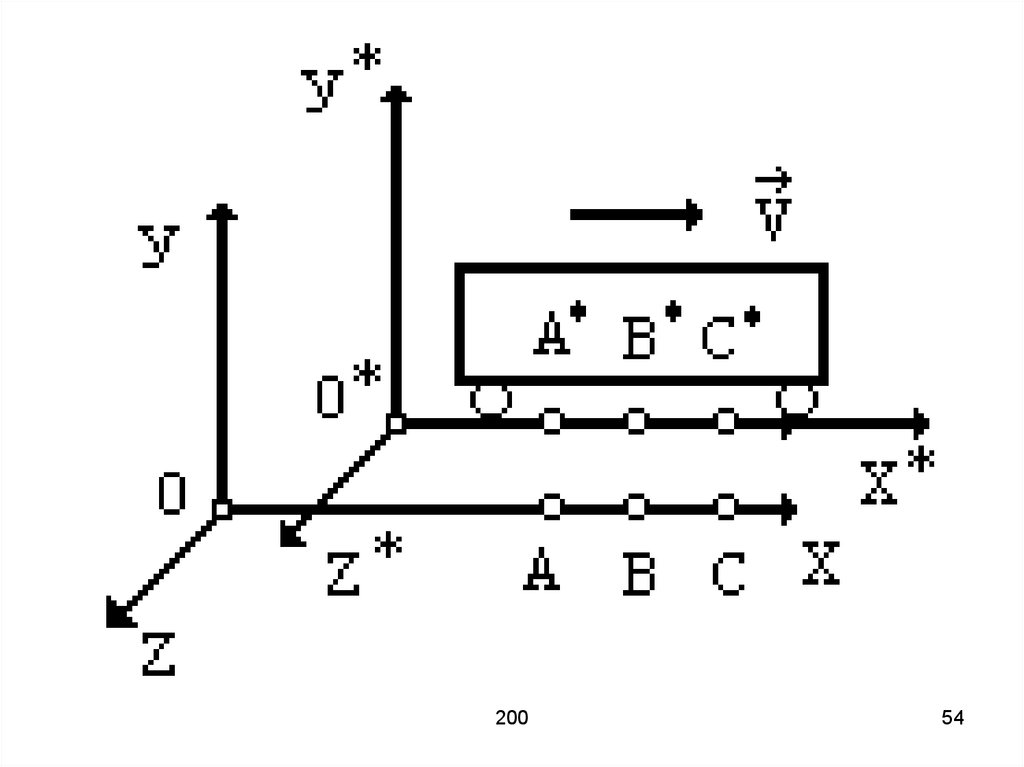
Пример: перрон – система K,
движущийся вагон со скоростью
ʋ = const – система K'.
200
53
54.
20054
55.
Для вагона точки обозначим черезА*, С* и В*, причем А*В*= В*С*. В тот
момент, когда одноименные точки
совпадают, в точках А и С
происходят два события, например
вспышка света. Из-за изотропности
пространства свет от точек А и С
дойдет до точки В одновременно.
200
55
56.
Наблюдатель же в точке В*,движущийся в направлении точки С*,
заметит вначале вспышку,
произведенную в точке С* и позднее
в точке А*.
200
56
57.
Наблюдатель на Земле, находясь вточке В увидит два пространственно
разделенных события,
произошедшие одновременно, тогда
как наблюдатель в точке В* заметит,
что событие в точках А* и С*
произойдут не одновременно.
200
57
58.
Следовательно, понятиеодновременности относительно, т. е.
два пространственно разделенных
события, одновременные в одной
ИСО не будут одновременными в
другой ИСО, движущейся
относительно первой равномерно и
прямолинейно со скоростью
ʋ = const.
200
58
59.
Это относится лишь к событиям,между которыми отсутствуют
причинно-следственная связь.
Причинно связанные события ни в
одной ИСО не будут
одновременными, так как во всех
ИСО событие, являющееся
причиной, всегда будет
предшествовать следствию.
200
59
60.
20060
61.
15. Преобразования Лоренца.Следствия из преобразований
Лоренца: сокращение длины
движущихся тел и замедление темпа
хода движущихся часов. Причинноследственная связь в СТО.
200
61
62.
Для описания движения в СТОиспользуют преобразования
Лоренца, позволяющие переходить
от координат одной инерциальной
системы отсчета к другой,
движущейся относительно первой
равномерно и прямолинейно и
обратно.
200
62
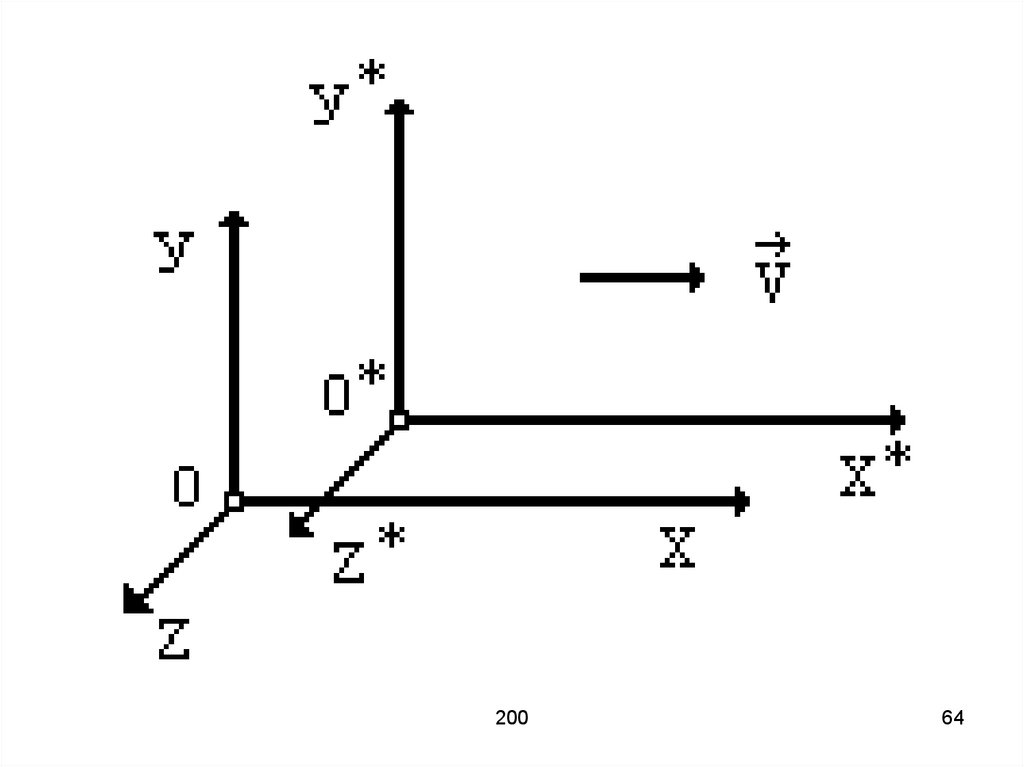
63.
Преобразования Лоренца имеютнаиболее простой вид в случае,
когда сходственные оси декартовых
координат неподвижной К и
движущейся К' инерциальных систем
отсчета попарно параллельны, и
если система К' движется
относительно системы К равномерно
и прямолинейно со скоростью
ʋ = const вдоль, например, оси Х.
200
63
64.
20064
65.
Начало отсчета времени выбираетсяв тот момент, когда координаты
начала 0 и 0' обеих инерциальных
систем отсчета К и К' совпадают,
т. е. t = 0 и t' = 0.
С учетом этого преобразования
Лоренца записываются в виде:
200
65
66.
x tx
;
2
1 ( / c)
y = y′;
x t
x
;
2
1 ( / c)
y′ = y;
z = z′;
z′ = z;
t x / c
t x / c
t
;
t
.
2
2
1 ( / c)
1 ( / c)
2
2
200
66
67.
Следствия преобразований Лоренца.Одновременность событий в разных
системах отсчёта.
В системе К в точках x1 и x2
происходят одновременно два
события в момент времени t1 = t2 = b;
200
67
68.
Но в системе К′ эти событияпроизойдут моменты времени:
b x1 / c
b x2 / c
t1
;
t
.
2
2
2
1 ( / c)
1 ( / c)
2
2
Но если события причинно
связанные, ни в одной из систем
следствие не произойдёт раньше
причины.
200
68
69.
Промежуток времени междусобытиями.
Существуют события, вызванные
причинно-следственной связью.
Например, чтобы камень упал в
воду, его нужно бросить.
200
69
70.
Бросок является причиной, ападение камня в воду – следствием.
1) сначала происходит событие,
являющееся причиной, а затем
происходит событие, являющееся
следствием первого;
2) если устранить событие,
являющееся причиной, то не
последует и другого события.
200
70
71.
В связи с этим в СТО, хотя время ипреобразуется, но
последовательность во времени
между причиной и следствием
сохраняется. Например, в ИСО,
связанной с Землей произошел
выстрел в момент времени t1 в точке
с координатой х1, а пуля попала в
мишень с координатой х2 в момент
времени t2.
200
71
72.
Тогда скорость пулиx x1
u
.
t2 t1
2
Используя преобразования Лоренца
найдем промежуток времени между
этими же событиями в ИСО системы
К′:
200
72
73.
(t2 t1 ) ( x2 x1 ) / ct2 t1
2
1 ( / c)
(t2 t1 ) u
1 2 ,
2
c
1 ( / c)
2
где скорости u и ʋ << c.
Так как t2 > t1, то и t′2 > t′1.
200
73
74.
Поэтому(t2 t1 )
t2 t1
2
1 ( / c)
если событие происходит в одной и
той же точке, т. е. х1 = х2.
Следовательно,
2
t t 1 ( / c) ,
200
74
75.
т. е. промежуток времени междудвумя событиями имеет меньшее
значение в ИСО, связанной с точкой,
где происходит событие.
В любой другой ИСО этот временной
интервал будет больше.
Вывод: В движущейся ИСО время
течёт медленнее.
200
75
76.
Промежуток времени Δt –собственное время тела, в системе,
где тело покоится. Собственное
время всегда меньше, чем время,
отсчитанное по часам, движущимся
относительно тела. Собственное
время – величина инвариантная.
200
76
77.
Эксперименты подтвердилиполученный результат.
Например, время жизни покоящихся
мюонов 2 мкс.
Мюоны же в потоках космических
лучей движутся относительно Земли
со скоростью ʋ = 0,991·c и успевают
пролететь расстояние не распадаясь
6 км, т. е. их время жизни с точки
зрения земного наблюдателя в
десятки раз больше.
200
77
78.
Длина тел в разных системах.Длина стержня в ИСО равна
разности координат его концов.
Например, λ = х2 – х1, причем
координаты х1 и х2 измеряются
одновременно (наблюдатель
покоится относительно стержня).
200
78
79.
Однако результат изменяется, когданаблюдатель и стержень движутся
относительно друг друга. Понятие
одновременности относительно и
события одновременные в одной
ИСО не будут одновременны в
другой ИСО, поэтому длина стержня
будет неодинаковой в различных
ИСО.
200
79
80.
Для вычисления длины стержняиспользуют преобразования
Лоренца.
Например, пусть некоторый
стержень расположен параллельно
оси Х в ИСО К, относительно
которой он покоится.
200
80
81.
В ИСО К′, движущейся относительноИСО К равномерно и прямолинейно
со скоростью ʋ = const длина этого
стержня:
λ′ = х′2 – х′1.
200
81
82.
Используя преобразования Лоренца,имеем
x1 t1
x1
;
2
1 ( / c)
x 2 t2
x2
,
2
1 ( / c)
то есть
( x 2 x1 ) υ(t2 t1 )
λ x2 x1
2
1 (υ/c)
200
82
83.
Если координаты концов отрезка вИСО К′ измерены одновременно
(так как t′2 = t′1.), то
λ
2
λ
;
λ
λ
1
(
υ
/
c
)
.
2
1 (υ/c)
λ – собственная длина, длина
измеренная в системе, где тело
покоится.
200
83
84.
Следовательно, длина отрезка влюбой ИСО, относительно которой
он движется, меньше длины отрезка
в неподвижной ИСО.
Однако это не означает, что
стержень деформируется в
движущейся ИСО.
200
84
85.
20085
86.
16. Закон сложения скоростей в СТО.Релятивистский импульс. Энергия
релятивистской частицы.
Инварианты преобразования
Лоренца. Интервал.
200
86
87.
ИнтервалЛюбые события характеризуются
точкой, где оно произошло, имеющей
координаты х, у, z и временем t, т. е.
каждое событие происходит в
четырехмерном пространствевремени с координатами х, у, z, t.
200
87
88.
В обычной механике рассматриваютпространственные координаты
отдельно от времени и расстояние
между двумя точками
( x2 x1 ) ( y2 y1 ) ( z2 z1 )
2
2
2
является инвариантной величиной
(не изменяется при переходе из
одной ИСО в другую ИСО).
200
88
89.
В релятивистской механике этавеличина не является инвариантной.
Приходится учитывать четвёртую
величину – время.
В четырёхмерном
пространстве-времени вводят
понятие интервал:
c (t2 t1 ) ( x2 x1 ) ( y2 y1 ) ( z2 z1 )
2
2
2
2
Интервал является инвариантом.
200
89
2
90.
Релятивистский закон сложенияскоростей:
u x
ux
ux
, u x
.
u x
u x
1 2
1 2
c
c
где ux – скорость м. т. (тела) в ИСО
К; u′x′ – скорость м. т. (тела) в К′; ʋ –
относительная скорость движения
ИСО К и К′. Все эти скорости
параллельны оси X.
200
90
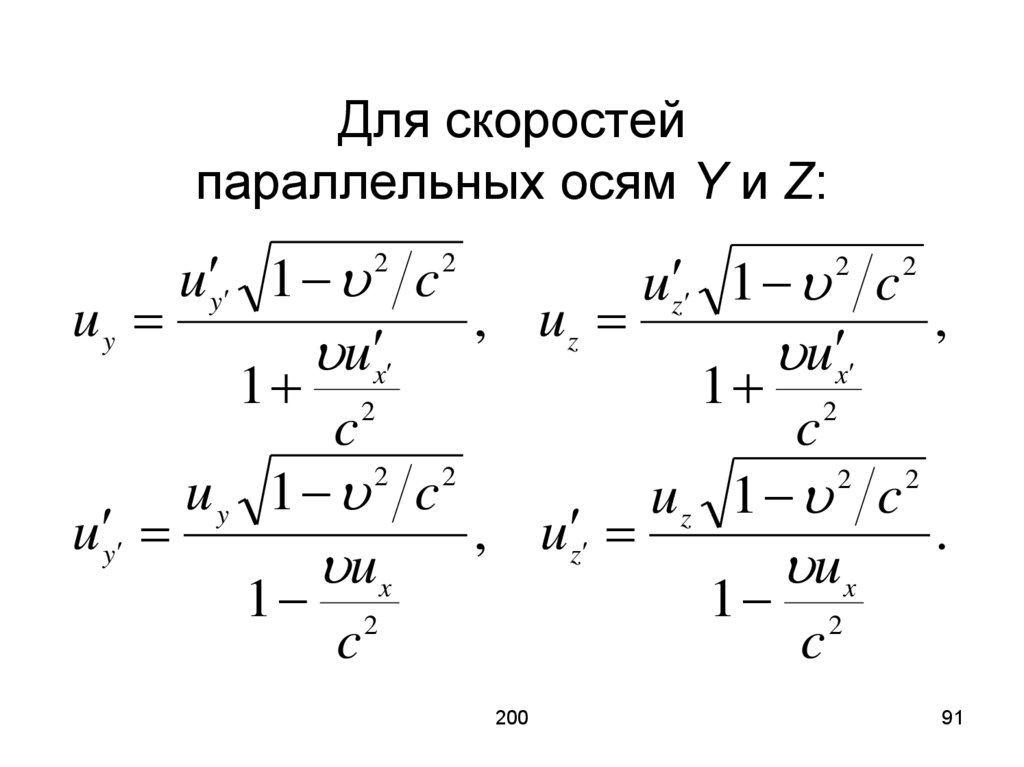
91.
Для скоростейпараллельных осям Y и Z:
2
2
u y 1 c
u z 1 c
uy
, uz
,
u x
u x
1 2
1 2
c
c
2
2
2
2
uy 1 c
uz 1 c
u y
, u z
.
u x
u x
1 2
1 2
c
c
2
2
200
91
92.
Релятивистский импульс в видеdr
p m0
dt
обеспечивает инвариантность
закона сохранения импульса по
отношению к преобразованиям
Лоренца,
200
92
93.
здесь dr – перемещение частицы(материальной точки) в той ИСО, в
которой определяется её импульс;
dt – время, определяемое по часам,
движущихся вместе с частицей
(собственное время).
200
93
94.
Так как,2
dt dt 1 ( / c) ,
то
m0dr
p
2
dt 1 ( / c)
где
dr
.
dt
200
94
95.
Следовательно, релятивистскийимпульс частицы
m0
p
2
1 ( / c)
200
95
96.
Уравнение динамикиdυ
m0
F m0
m0 a
a
2
dt
1 с
200
96
97.
ЭнергияЭнергия покоя
E0 = m0c2,
Энергия релятивистской частицы
E E0
2
1
m0c
2
2
1 ( /c)
1 ( /c)
m0 – масса покоя.
200
97
98.
Кинетическая энергиярелятивистской частицы
2
m0c
2
T
m
c
E
E
0
0
2
1 ( /c)
p c T T 2m0c
2 2
200
2
98
99.
Полная энергияE c p m c m0c 1 p m0c
2
2
0
2
2
2
E m0c p 2m0 m0c T
2
2
2
200
99
100.
Инварианта энергии и импульсаE p c m c inv
2
2
2
2
0
4
2
E
2
2
2
2 2
px p y pz m0 c inv
2
c
Величина E/c, px, py, pz образует
четырёхвектор (вектор энергииимпульса).
200
100
101.
Рассмотрим неупругое соударениедвух тел массой m каждое.
Относительно системы К′ тела
движутся навстречу друг другу со
скоростью ʋ1 = – ʋ2 = ʋ0.
К′
mʋ1
К
mʋ2
ʋ0
x′
x
200
101
102.
Система К′ движется относительносистемы К со скоростью ʋ0.
В системе К′
p1 p 2 0
В системе К
p1 p2 p1 ,
200
p2 0.
102
103.
Согласно переходу1 x 0 0 0
2 0
1x
2
0 1 x
0 0
0
1 2
1 2
1 2
c
c
c
0 0
2 x
0
0 0
1
2
c
импульс до удара будет
2m 0
m 1x m 2 x
2
2
1 0 c
200
103
104.
Илиm 1
p1
2
1 ( 1/c)
заменяя скорость ʋ1 на ʋ0:
2m 0 1 /c
p1
2
2
( 0 c)
1
1
1
2
2
1 0 /c
с
m 1
2
0
200
2
m 0
0
1
с
2
104
105.
Но должно быть2m 0
p
2
1 ( 0 c)
200
105
106.
Такой результат получили, так как неучли массу системы
2m
2
M
,
2
m
M
1
(
c
)
.
0
2
1 ( 0 c)
200
106
107.
Это обусловлено тем, чтокинетическая энергия частиц
превратилась в эквивалентное
количество энергии покоя, а это в
свою очередь привело к
возрастанию массы на Δm = ΔE0/c2.
Изменение массы связано с
энергией. Сама же масса является
инвариантной величиной.
200
107
108.
200108
109.
ЛЕКЦИЯ № 6Элементы механики твёрдого тела.
200
109
110.
ВОПРОСЫ17. Условия равновесия твёрдого
тела. Мгновенная ось вращения.
18. Кинетическая энергия
вращающегося твёрдого тела.
Работа момента силы.
200
110
111.
19. Основной закон динамикивращательного движения твёрдого
тела. Момент инерции, его свойства.
Теорема Штейнера (теорема о
параллельных осях).
20. Закон сохранения момента
импульса изолированной системы.
Изотропность пространства и закон
сохранения момента импульса.
Гироскоп.
200
111
112.
17. Условия равновесия твёрдоготела. Мгновенная ось вращения.
200
112
113.
В случае описания положения и/илидвижения материальной точки
достаточно 3-х степеней свободы.
Степень свободы – число
независимых координат,
требующихся для однозначного
определения положения тела.
200
113
114.
Для абсолютно твёрдого тела (тело,деформациями которого можно
пренебречь) необходимо 6 степеней
свободы: 3 – положение в
пространстве, 3 – ориентация в
пространстве.
Запишем уравнения твёрдого тела в
векторном виде
(2 уравнения вместо 6).
200
114
115.
Уравнение динамики движенияцентра
масс
d
m
Fвнеш
dt
Уравнение динамики вращательного
движения
dL
M внеш
dt
200
115
116.
Если Fвнеш и Mвнеш равны нулю, тотело будет находиться в равновесии.
Условия равновесия твёрдого тела:
d
m
Fвнеш
dt
dL
0,
M внеш 0.
dt
200
116
117.
Не всегда можно пользоватьсямоделью абсолютно твёрдого тела.
Пример: рассмотрим балку на 3-х
опорах. Для данной системы можно
записать только два уравнения
равновесия
F1 + F2 + F3 = P,
F2 · ℓ + F3 · x = P · ℓ · 1/2.
200
117
118.
F1F3
F2
P
x
ℓ
Здесь два уравнения и три
неизвестных: F1, F2, F3 .
200
118
119.
Данная задача оказаласьнеопределённой, решить её можно,
если придать одной из сил
произвольное значение.
Механические системы, подобные
данной, называются статически
неопределёнными.
200
119
120.
Физики про себя шутят: если им датьзадачу о равновесии стола на 4
ножках, то они, почти сразу, выдадут
ответ о столе на 1 ножке, спустя
некоторое время о столе с
бесконечным числом ножек, и будут
бесконечно долго решать задачу о
равновесии стола на 4 ножках.
200
120
121.
Любое движение твёрдого теламожет быть представлено как
наложение двух типов движения:
поступательного и вращательного;
соответственно скорость тела можно
представить в виде
0 0 ω r
ʋ0 – поступательная скорость, ʋ/ –
скорость, обусловленная
вращением
ω r
200
121
122.
Элементарное перемещениетвёрдого тела при плоском движении
всегда можно представить как
поворот вокруг некоторой оси,
называемой мгновенной осью
вращения. Мгновенная ось может
находиться как в самом теле, так и
вне его. Мгновенная ось меняет своё
положение относительно тела и
относительно неподвижной системы
отсчёта.
200
122
123.
Пример: катящийся цилиндр.Плоское движение твёрдого тела
можно рассматривать как ряд
последовательных элементарных
вращений вокруг мгновенных осей.
Пример неплоского движения:
пропеллер самолёта совершает
вращение вокруг своей оси и
поступательное движения вдоль
этой оси.
200
123
124.
ωdφ
ʋ
ʋ
O/
O
200
124
125.
200125
126.
18. Кинетическая энергиявращающегося твёрдого тела.
Работа момента силы.
200
126
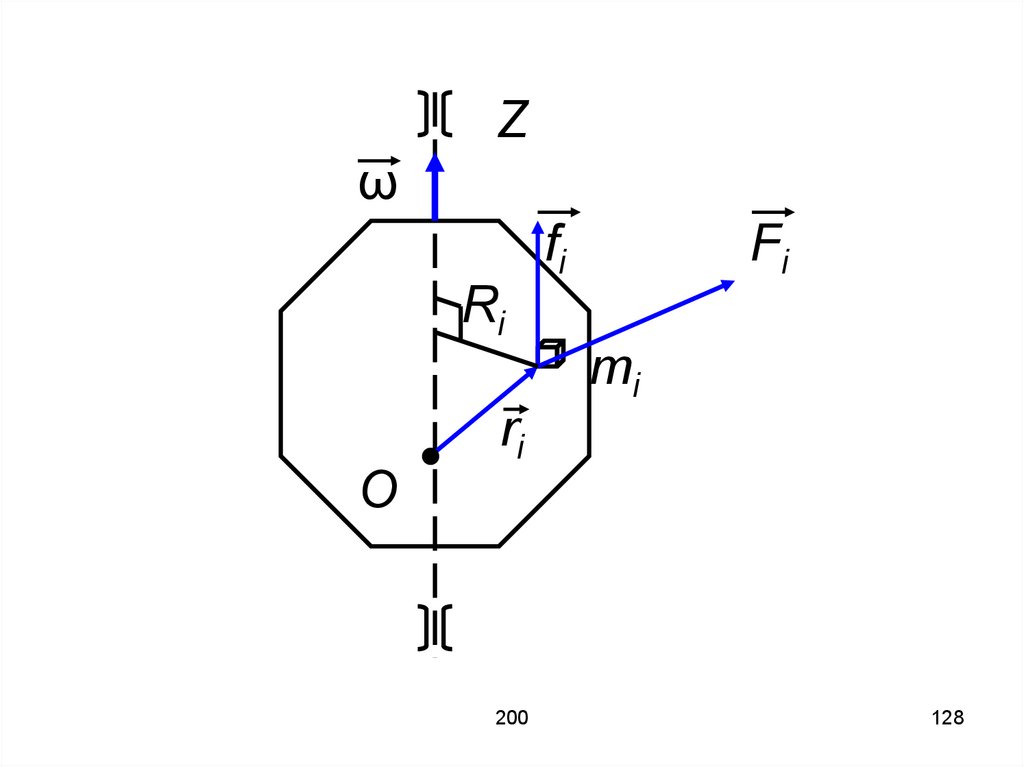
127.
Получим выражение длякинетической энергии вращающегося
тела. Рассмотрим вращение тела
вокруг неподвижной оси Z.
Линейная скорость элементарной
массы mi равна ʋi = ωRi, Ri –
расстояние от массы mi до оси Z, ω –
угловая скорость вращения.
200
127
128.
Zω
fi
Fi
Ri
mi
ri
O
200
128
129.
Кинетическая энергия элементарноймассы mi:
mi
1
2 2
Eki Ti
mi ω Ri
2
2
2
i
Кинетическая энергия всего тела:
1 2
1 2
Iω
2
T Ti ω mi Ri ω I
2
2
2
i
200
2
129
130.
Рассмотрим силы, действующие наэлементарную массу mi: внешние Fi,
внутренние fi (эти силы
перпендикулярны оси вращения,
иначе будет сдвиг вдоль оси Z).
Сумма моментов внутренних сил
равна нулю. Суммарный момент
внешних сил приведёт к совершению
работы.
200
130
131.
dAr F ωdt Mωdt M ωωdt M ωd
С другой стороны, работа внешних
сил идёт на приращение
кинетической энергии вращения:
Iω
d A dT d
Iωdω
2
Iωεdt Mωdt
2
200
131
132.
Так, мяч или обруч, брошенныйгоризонтально без вращения,
раскрутится. Кинетическая энергия
вращения получится за счёт
действия силы трения, точнее за
счёт действия пары сил: силы трения
и силы инерции. Произойдёт
частичный переход энергии
кинетической энергии
поступательного движения в
кинетическую энергию вращения.
200
132
133.
И наоборот, раскрученный обруч,опущенный на горизонтальную
опору, приобретёт горизонтальную
скорость за счёт работы силы
трения. При движении без
проскальзывания выполняется
соотношение: ʋ = ωR. Если сила
трения равна нулю, то в первом
случае тело будет скользить без
вращения, во втором – крутиться на
одном месте.
200
133
134.
Теперь вычислим кинетическуюэнергию, поступательную и
вращательную при плоском
движении.
Скорость i-й элементарной
массы
i 0 ω ri
ʋ0 – поступательная скорость
некоторой точки О, связанной с
телом, например, центра масс.
ri – радиусвектор i-й элементарной
массы относительно точки О.
200
134
135.
Получим выражение длякинетической энергии твёрдого тела:
2
mi
1
Eki Ti
mi 0 ω ri
2
2
2
1
2
mi 0 2 0 ω ri ω ri ,
2
2
i
200
135
136.
Отметим следующее:ω ri ω Ri
Ri – расстояние от точки с массой mi
до оси вращения.
2 0 ω ri 2 0 ω ri
Запишем кинетическую энергию
всего тела с учётом приведённых
замечаний:
200
136
137.
здесь Σmi = m – масса всего тела,mi ri mrc
если в качестве точки О взять центр
масс, то rc = 0.
Момент инерции относительно
центра масс (наименьший при
данной ориентации):
m R
i
2
i
I0 Ic
200
137
138.
В итоге получили выражениекинетической энергии
поступательного и вращательного
движения (ось вращения проходит
через центр масс):
m
I cω
Ek T
2
2
2
c
200
2
138
139.
200139
140.
19. Основной закон динамикивращательного движения твёрдого
тела. Момент инерции, его свойства.
Теорема Штейнера (теорема о
параллельных осях).
200
140
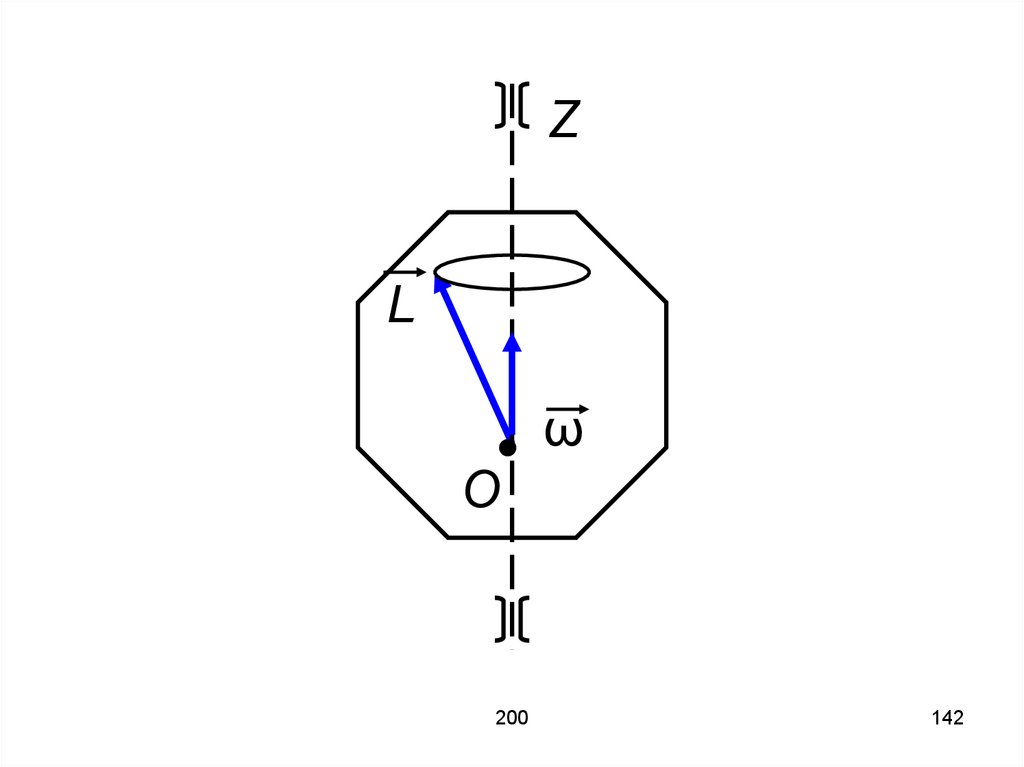
141.
Рассмотрим вращение тела вокругнеподвижной оси
dL
M внеш
dt
dLZ
M Zвнеш Iε Z
dt
В общем случае вектор L не
совпадает по направлению с осью
вращения Z и поворачивается
вместе с телом вокруг этой оси,
описывая конус.
200
141
142.
ZL
ω
O
200
142
143.
В случае однородного тела,симметричного относительного оси
вращения, момент импульса
относительно точки O, лежащей на
оси вращения, совпадает по
направлению с осью. В этом случае
L LZ ωI
случай вращения вокруг оси
симметрии,
LZ ω Z I
в общем случае.
200
143
144.
Момент инерции зависит от выбораоси.
Свободная ось – ось, положение
которой в пространстве остаётся
неизменным при вращении вокруг
неё тела в отсутствии внешних сил.
Главные оси – для любого тела
существует 3 взаимно
перпендикулярных свободных оси,
проходящие через центр масс.
200
144
145.
200145
146.
Вычислим момент инерцииоднородного шара. Разобьём его на
бесконечно тонкие сферические
слои толщиной dr.
Масса шара m. Радиус шара R.
Масс сферического слоя
dm = m · dV/V.
Объём сферического слоя
dV = 4πr2 · dr.
Момент инерции сферического слоя
dI = 2/3 dm · r.
200
146
147.
Rdr
200
147
148.
Момент инерции шара складываетсяиз моментов инерции сферических
слоёв:
R
R
R
4
2 2
r
I dI r dm 2m 3 dr
R
0
0 3
0
5 R
R
2m 4
2m r
2
2
3 r dr 3
mR
R 0
R 50 5
200
148
149.
Если происходит параллельныйперенос оси вращения, то момент
инерции увеличивается, согласно
теореме Штейнера:
I I c ma
2
IC – момент инерции тела,
относительно оси, проходящей через
центр масс, это минимальный
момент инерции при данной
ориентации, m – масса тела, a –
расстояние между осями.
200
149
150.
Моменты инерции:момент инерции кольца (обруча)
mR
2
2mR
200
2
mR
2
2
150
151.
Момент инерции дискаmR
2
2
3mR
2
200
2
mR
4
2
151
152.
Момент инерции шара и сферы2
2
mR
5
2
2
mR
3
200
152
153.
Момент инерции стержня1
2
mL
12
1 2
mL
3
200
153
154.
200154
155.
20. Закон сохранения моментаимпульса изолированной системы.
Изотропность пространства и закон
сохранения момента импульса.
Гироскоп.
200
155
156.
Из основного уравнения динамикивращательного движения
L M
Можно получить закон сохранения
момента импульса (аналогично
закону сохранения импульса).
В замкнутой системе (M = 0)
суммарный момент импульса
остаётся
постоянным.
L const
143
156
157.
Пространство однородно,следовательно, параллельный
перенос системы из одного места в
другое не изменяет свойств системы
– закон сохранения импульса
нарушаться не будет.
143
157
158.
Пространство изотропно,следовательно, поворот замкнутой
системы как целого не отражается
на её механических свойствах –
закон сохранения момента импульса
нарушаться не будет.
143
158
159.
Как правило, момент инерции неизменяется (I = const),
следовательно, в силу закона
сохранения импульса угловая
скорость тоже остаётся постоянной
ω = const.
200
159
160.
Если же момент инерции можноизменять, то угловая скорость тоже
изменяется. Например, можно
увеличить скорость вращения
стержня, перемещая грузы на
стержне к оси вращения.
200
160
161.
Гироскоп (волчок) – массивноесимметричное тело, вращающееся с
большой скоростью вокруг оси
симметрии (ось гироскопа).
При попытке вызвать поворот
гироскопа наблюдается
гироскопический эффект: поворот
вокруг оси параллельной
направлению действия сил, т.е.
перпендикулярно оси поворота.
200
161
162.
dLF1
L/
L
dφ
M
Z
Y
F2
X
200
162
163.
Пара сил F1 и F2 (F1 = F2)перпендикулярны плоскости рисунка
(ось X), пытаются повернуть тело
(или придать вращение) вокруг
горизонтальной оси (ось Y), момент
сил M направлен влево,
следовательно, приращение
момента импульса dL будет также
направлено влево.
200
163
164.
Поскольку момент импульса L былнаправлен вертикально вверх
(ось Z), а его приращение
направлено влево, то получается что
вектор момента импульса L, будет
поворачиваться вокруг оси X против
часовой стрелки (вектор L переходит
в вектор L′).
200
164
165.
В самом делеdL M dt , dL M ,
L L dL.
200
165
166.
Угол поворота и угловая скоростьповорота оси вращения:
dL
dt
d
M
L
L
d M
ω
M ω L .
dt
L
200
166
167.
Момент силы, вызывающий поворотоси гироскопа, угловая скорость
поворота и момент инерции связаны
следующим выражением
M ω L
200
167
168.
Например, волчок, раскрученный вполе тяжести Земли будет
испытывать поворот оси вращения.
В поле сил тяжести ось гироскопа с
неподвижной точкой поворачивается
вокруг вертикальной оси, описывая
конус. Такое движение называется
прецессией.
200
168
169.
200169
170.
ЛЕКЦИЯ № 7Элементы динамики сплошных
сред.
200
170
171.
ВОПРОСЫ21. Элементы гидродинамики.
Идеальная несжимаемая жидкость.
Уравнение неразрывности струи.
Уравнение Бернулли. Основное
уравнение гидростатики. Уравнение
Эйлера.
22. Течение вязкой несжимаемой
жидкости в трубе. Формула
Пуазейля. Ламинарное и
турбулентное течение.
200
171
172.
200172
173.
Основные определенияС точки зрения механики жидкости и
газы могут быть определены как
такие среды, в которых при
равновесии касательные
напряжения существовать не могут.
Pτ = 0
Pn ≠ 0
200
173
174.
Газы занимают весьпредоставленный объём. Жидкость
обладает собственным объёмом,
который изменяется лишь
незначительно с изменением
внешнего давления.
Идеальная жидкость – жидкость, в
которой внутреннее трение
(вязкость) полностью отсутствует.
200
174
175.
Для описания движения жидкостиуказывают для каждой точки
пространства вектор скорости как
функцию времени.
200
175
176.
Совокупность векторов ʋ, заданныдля всех точек пространства,
образует поле вектора скорости.
Линии тока – линии, касательные к
которым совпадают с векторами ʋ.
Густота линий пропорциональна
модулю скорости.
Стационарное течение – если вектор
скорости в каждой точке остаётся
постоянным.
200
176
177.
200177
178.
Векторные поляГрадиент – вектор, направленный в
сторону наибольшего изменения
поля.
Если каждой точке P с координатами
x, y, z, сопоставляется значение
скалярной величины φ = φ(x, y, z),
говорят, что задано скалярное поле
φ.
grad i
j
k
y
z
x
200
178
179.
Поток вектораS cosα,
d dS cosα dSn
dS
200
n
α
179
180.
Можно сравнить с потоком жидкости:V
1
S cosα t
t
t
Поток вектора «a» через
поверхность S
a adSn andS
S
S
Если вектор входит в область,
ограниченную поверхностью S, то
ставят знак «+», если выходит –
ставят знак «–».
200
180
181.
Дивергенция (divergentia (лат) расхождение) – величина, численноравная плотности точек, в которых
начинаются (+)
либо оканчиваются (–) линии поля.
200
181
182.
adiva
,
V
1
diva lim adS .
V 0
VS
Рассмотрим дивергенцию некоторой
точки с точки зрения трёхмерного
пространства. Выделим некоторую
точку, объём которой равен
Δx·Δy·Δz.
200
182
183.
aΔZ
Z
Y
ΔY
X
200
ΔX
183
184.
a ax y z a y x z az x yax a y az
V
x y z
ax a y az
V
a
z
y
x
a ax a y az
diva
V x y z
200
184
185.
Теорема Остроградского-Гаусса(Теорема Гаусса):
Поток вектора a сквозь замкнутую
поверхность S равен алгебраической
сумме источников поля (дивергенция
вектора a) заключённых внутри этой
поверхности в объёме V.
Дивергенция – мощность источников
поля, отнесённая е единице объёма.
200
185
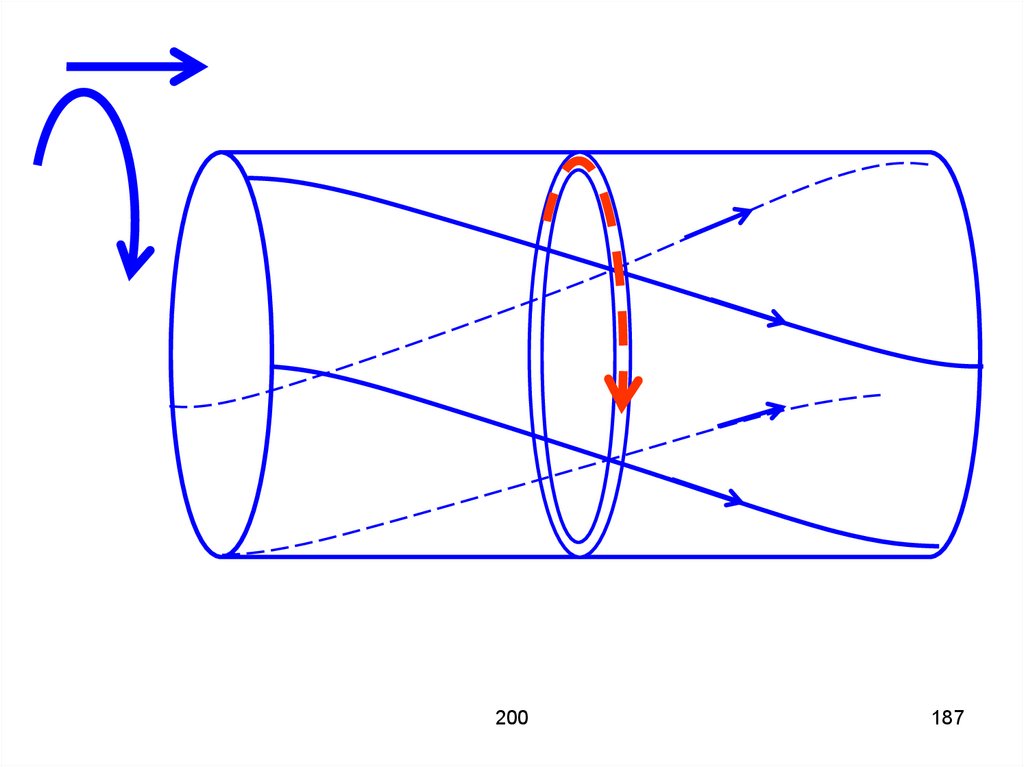
186.
ЦиркуляцияРассмотрим какой-нибудь канал в
потоке. Если весь поток заморозить,
оставить только этот канал, то в нём
может сохраниться движение.
Циркуляция – это произведение
скорости жидкости на длину контура.
a
d
a
d
L
L
200
186
187.
200187
188.
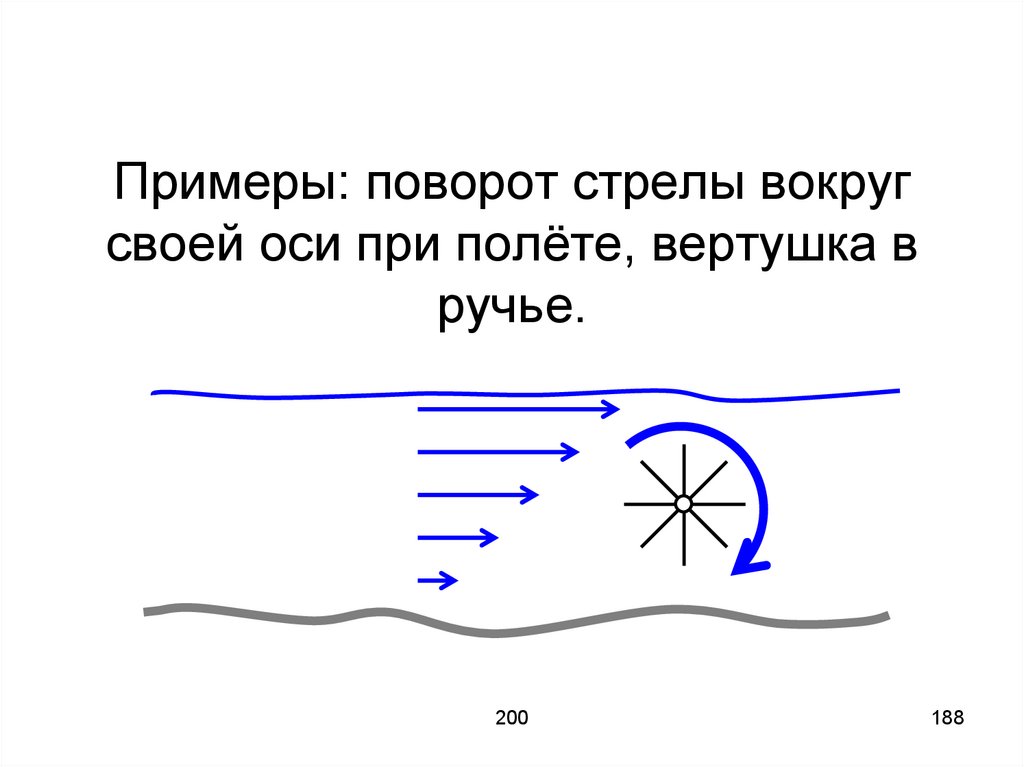
Примеры: поворот стрелы вокругсвоей оси при полёте, вертушка в
ручье.
200
188
189.
Ротор – плотность порожденияциркуляции.
1
rota n lim
ad
S 0
S L
200
189
190.
az a yrota x ,
y
z
ax az
rota y ,
z
x
a y ax
rota z .
x y
200
190
191.
irota
x
ax
200
j
y
ay
k
z
az
191
192.
Теорема Стокса:Циркуляция вектора a по
произвольному контуру L равна
потоку вектора rota через
произвольную поверхность S,
ограниченную данным контуром.
a
d
rot
a
d
S
n
L
200
192
193.
200193
194.
21. Элементы гидродинамики.Идеальная несжимаемая жидкость.
Уравнение неразрывности струи.
Уравнение Бернулли. Основное
уравнение гидростатики. Уравнение
Эйлера.
200
194
195.
Рассмотрим идеальную жидкость(жидкость, в которой внутреннее
трение (вязкость) полностью
отсутствует). Также, будем считать,
что жидкость несжимаемая.
200
195
196.
Рассмотрим бесконечно малыйобъём жидкости в виде цилиндра,
ось цилиндра II оси X.
dx
P(x)
P(x+dx)
200
196
197.
Силы давления на боковуюповерхность не учитываем, так как
их проекция на ось X равна нулю.
Остаётся давление, действующее на
основания, вычислим суммарную
силу давления
[P(x) – P(x+dx)]dS.
200
197
198.
Разность в скобках можно заменитьдифференциалом:
dP
P
P x P x dx dS dxdS dV
dx
x
P
– частная производная
x
(y, z, t = const).
200
198
199.
Таким образом, на единицу объёмабудут действовать сила F:
P
P
P
Fx , Fy , Fz
x
y
z
или
F gradP.
200
199
200.
В состоянии равновесия сила F(сила давления) должна
уравновешиваться силой f
(сила f – объёмная плотность
массовых сил, то есть зависит от
массы, пример f = ρg – сила
тяжести).
200
200
201.
Основное уравнение гидростатики:f grad P
Уравнение Эйлера:
d
ρ
f gradP
dt
200
201
202.
Основное уравнение гидростатикиgradp = f,
здесь p – давление жидкости, f –
объёмная плотность массовых сил.
Пример – сила тяжести
Fт mg
f
ρg
V
V
здесь V – объём, m – масса, g –
ускорение свободного падения,
ρ – плотность жидкости.
200
202
203.
Уравнение ЭйлераdV
ρ
f gradp
dt
здесь dV – дифференциал скорости
потока жидкости, dV/dt – ускорение
жидкости в данной точке
пространства.
Для равновесия жидкости
необходимо, чтобы силовое поле, в
котором она находится, было
консервативным.
200
203
204.
Условие неразрывности жидкостиРассмотрим стационарный поток
идеальной несжимаемой жидкости,
рассмотрим некоторую трубку тока,
ограниченную линиями тока,
например, трубу с переменным
сечением.
200
204
205.
Поскольку жидкость несжимаема,объём входящий равен объёму
выходящему, но поперечное сечение
изменяется, это приводит к
изменению скорости:
V1 = V2,
S1 · ʋ1 · t = S2 · ʋ2 · t = const,
S · ʋ = const.
Это и есть условие неразрывности
жидкости.
200
205
206.
S1S2
1
2
линии тока
трубка тока
200
206
207.
Уравнение БернуллиЕщё раз рассмотрим некоторую
трубку тока.
В силу неразрывности
ΔV1 = ΔV2 = ΔV.
200
207
208.
200208
209.
Так как нет сил трения, топриращение энергии выделенного
объёма равно:
2
2
ρ V 1
ρ V 2
E
ρ Vgh1
ρ Vgh2
2
2
и работа сил давления на площадки
S1 и S2
A p1S1 1 p2 S2 2 p1 p2 V
равна изменению энергии.
200
209
210.
Приравниваем ΔE и A, делим на ΔV,получаем уравнение Бернулли:
ρ
ρ
ρgh1 p1
ρgh2 p2 const
2
2
2
1
2
2
200
210
211.
Уравнение Бернулли объясняетразность давления в трубке тока с
переменным сечением.
200
211
212.
200212
213.
200213
214.
22. Течение вязкой несжимаемойжидкости в трубе. Формула
Пуазейля. Ламинарное и
турбулентное течение.
200
214
215.
Рассмотрим две плоские пластины,S – площадь пластинок,
ℓ – длина пластинок,
d – расстояние между пластинами.
Одна движется со скорость ʋ под
действием некоторой силы F.
Динамометр у нижней пластины,
неподвижной, спустя некоторое
время покажет усилие, действующие
на неподвижную пластину, равное F.
200
215
216.
ZS
ʋ
F
F
108
216
217.
Сила передаётся за счёт трениямежду слоями жидкости
(вязкое трение)
d
F η S
dz
η – коэффициент вязкости или
внутреннего трения (динамическая
вязкость),
размерность – Па·с (СИ),
Пуаз (СГС),
1 Па·с = 10 П.
108
217
218.
Стационарное течение вязкойжидкости
Ламинарное течение – течение
жидкости как бы отдельными
слоями, которые не
перемешиваются.
Турбулентное течение – течение,
при котором происходит энергичное
перемешивание слоёв жидкости.
200
218
219.
При течении в трубе (радиус трубыR) в центре трубы (r = 0) скорость
максимальна ʋmax. На стенке трубы
скорость равна нулю (r = R).
Зависимость скорости вязкой
жидкости от радиуса r (расстояние от
оси трубы):
p1 p2 2 2
R r
4ηL
200
219
220.
здесь p1 и p2 – давление на входе ивыходе трубы, η – коэффициент
вязкости, L – длина трубы, ρ –
плотность жидкости.
L
R
p1
r
p2
200
220
221.
Поток жидкости через трубу за однусекунду (формула Пуазейля)
p1 p2 4
Q π
R
8ηL
200
221
222.
Формула Пуазейля справедлива дляламинарного течения. Если число
Рейнольдса меньше определённого
значения, то течение жидкости
считают ламинарным, если значение
больше, то течение турбулентное.
Число Рейнольдса:
ρ 0 0
Rе
η
ν
ν η ρ – кинематическая вязкость.
200
222
223.
200223






























































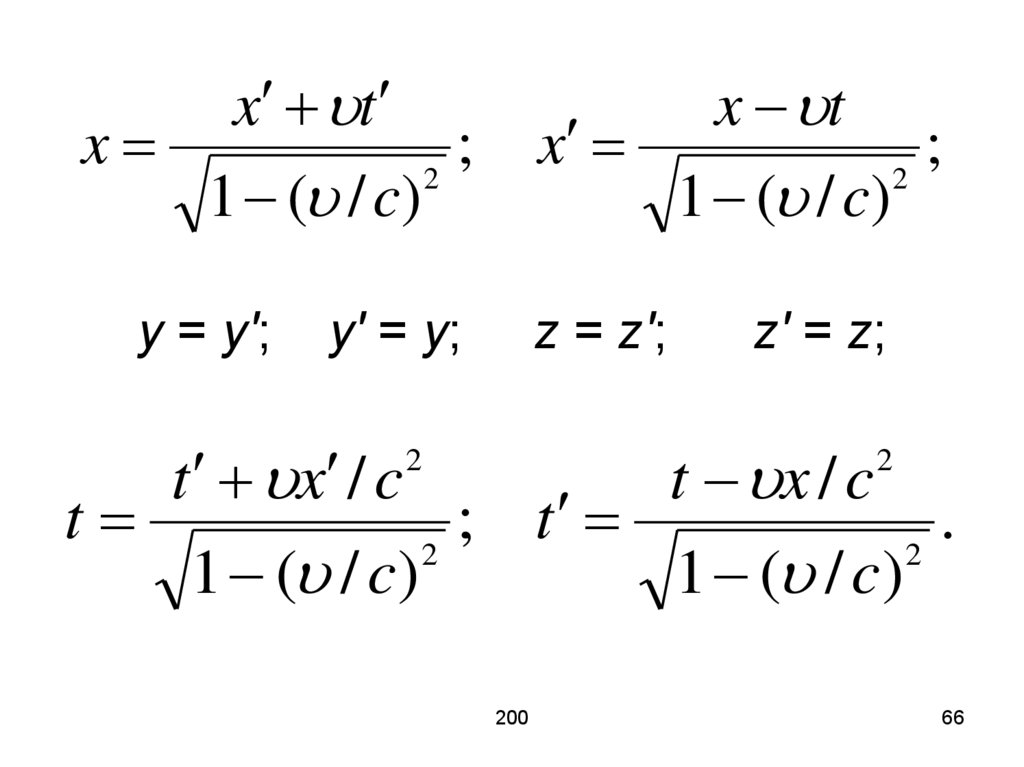






















































































































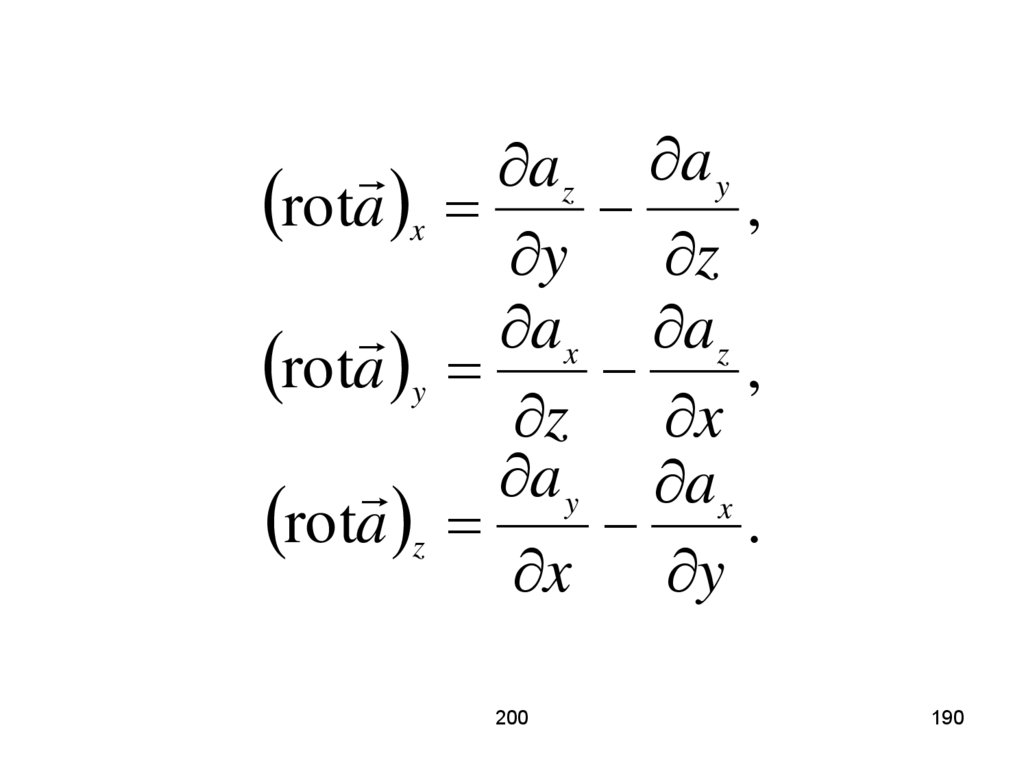

































 Физика
Физика








