Углы с сонаправленными сторонами. Угол между прямыми

1.

Жизнь не спросит,
что ты учил.
Жизнь спросит,
что ты знаешь.

2.

3.

4.

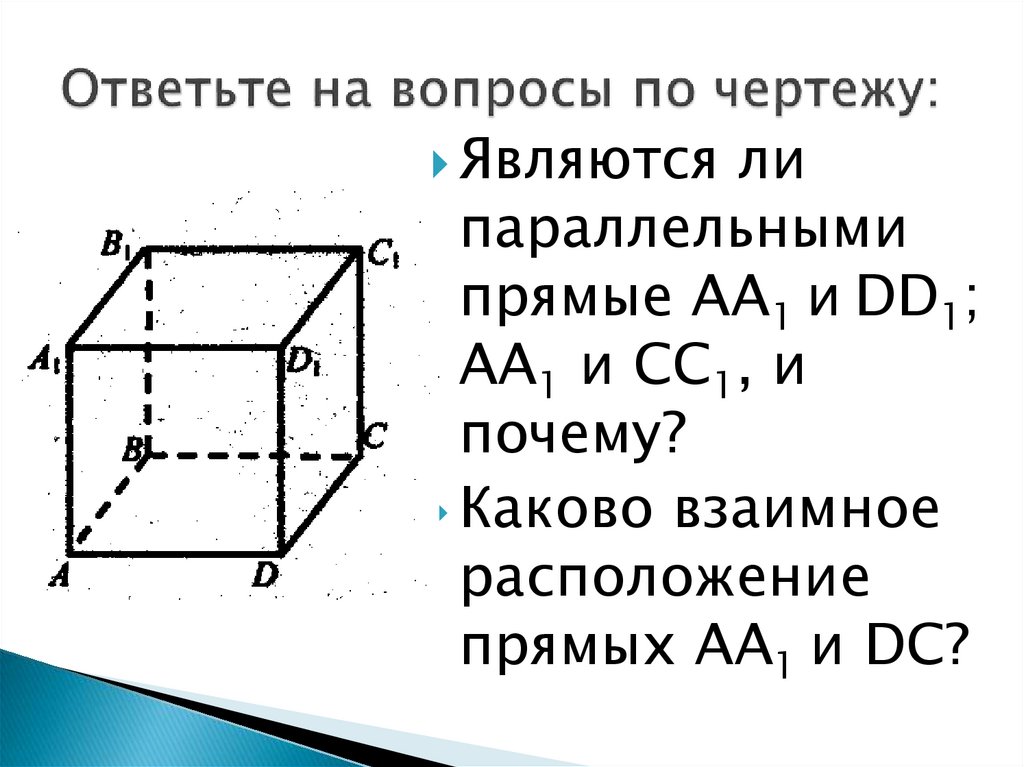
Являются
ли
параллельными
прямые АА1 и DD1;
АА1 и CC1, и
почему?
Каково взаимное
расположение
прямых AA1 и DС?

5.

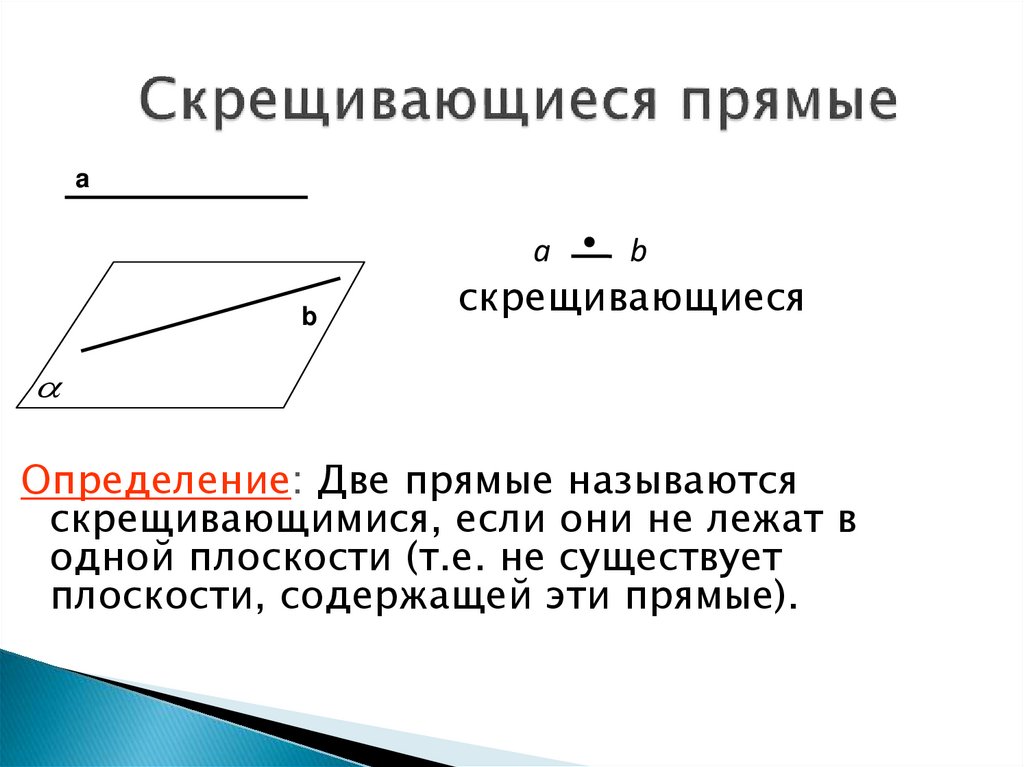
a
a
b
b
скрещивающиеся
Определение: Две прямые называются
скрещивающимися, если они не лежат в
одной плоскости (т.е. не существует
плоскости, содержащей эти прямые).

6.

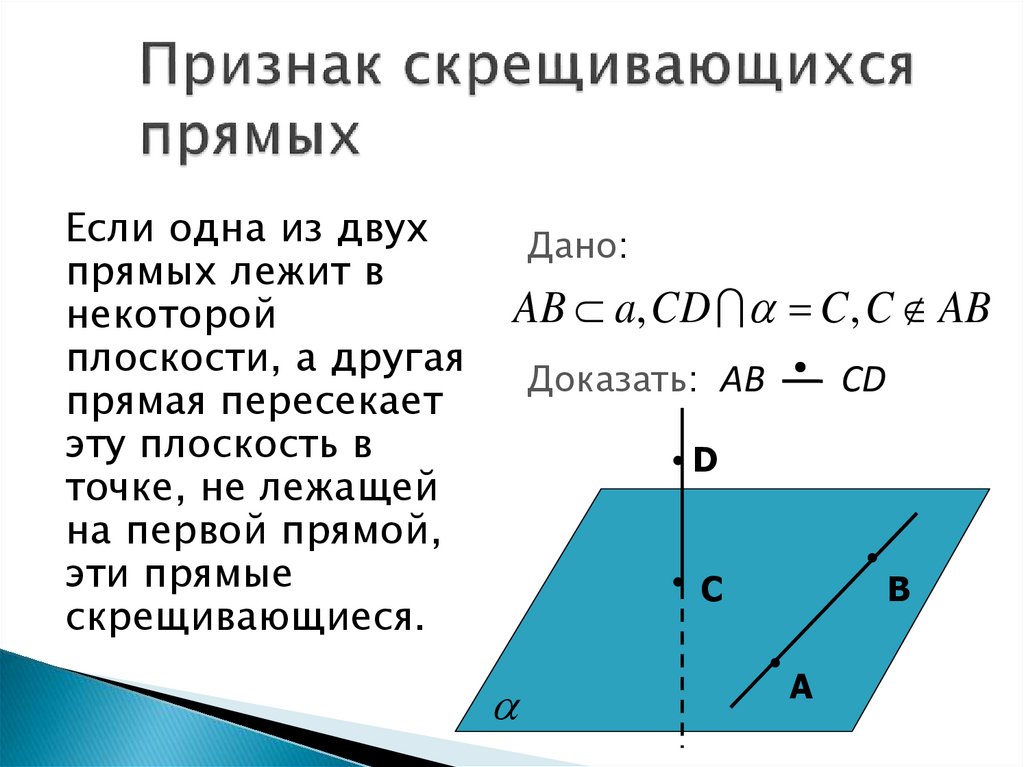
Если одна из двух
прямых лежит в
некоторой
плоскости, а другая
прямая пересекает
эту плоскость в
точке, не лежащей
на первой прямой,
эти прямые
скрещивающиеся.
Дано:
AB a, CD C , C AB
Доказать: AB
CD
D
C
B
A

7.

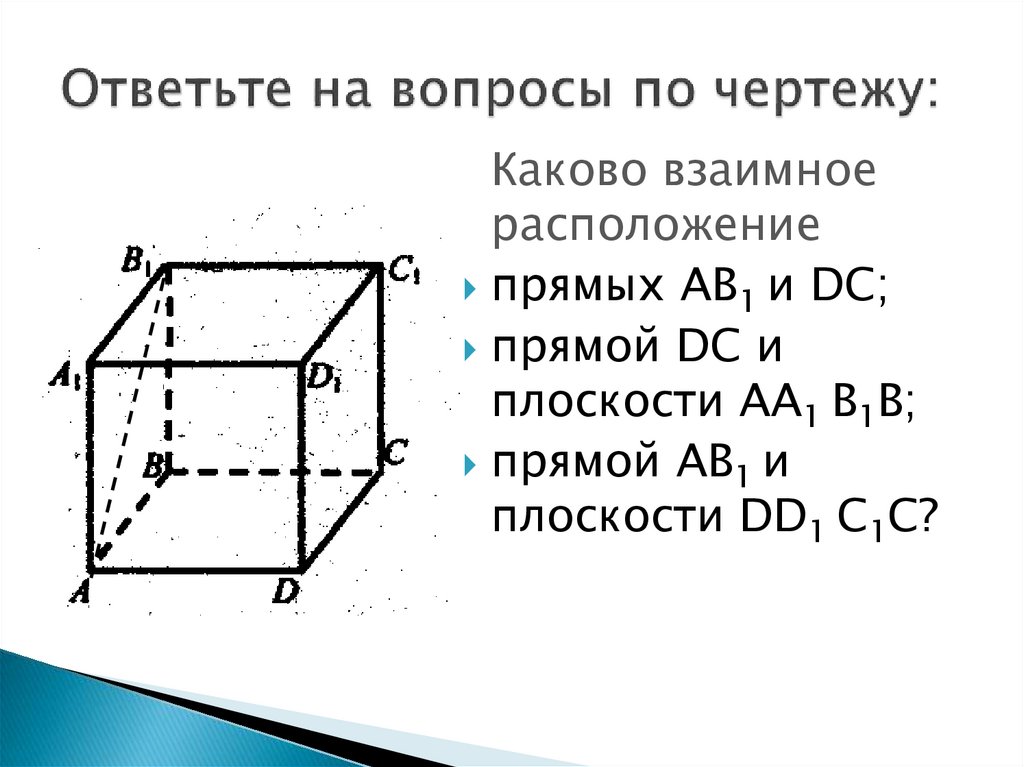
Каково взаимное
расположение
прямых AB1 и DС;
прямой DС и
плоскости AА1 B1В;
прямой AB1 и
плоскости DD1 C1C?

8.

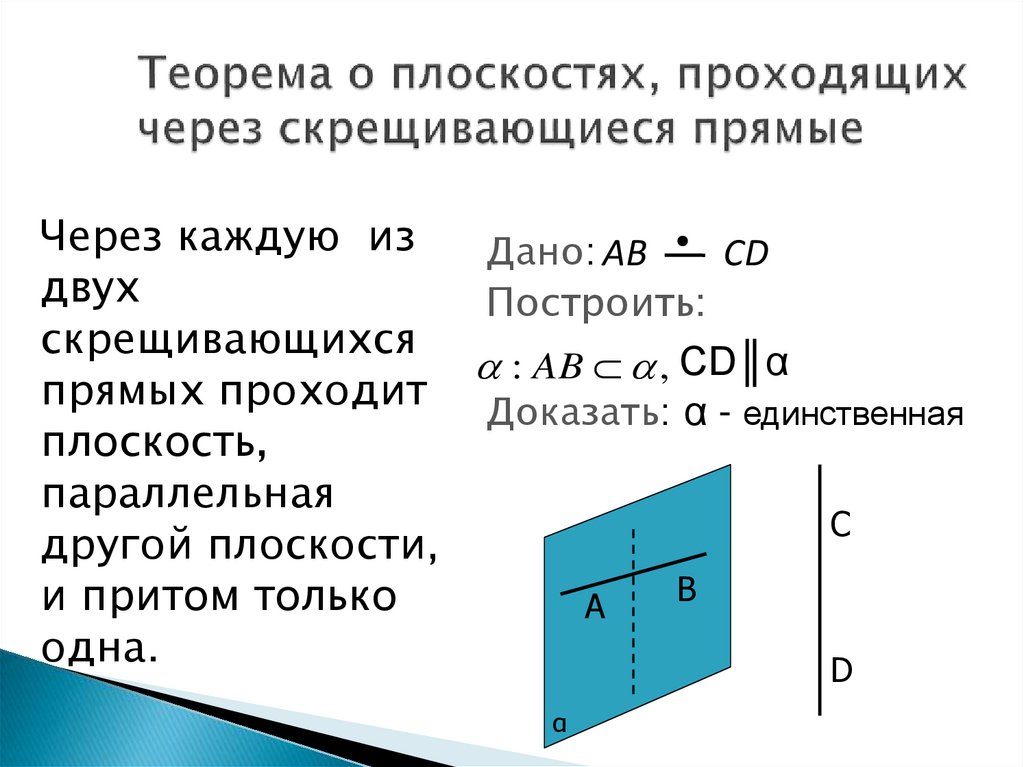
Через каждую из
Дано: AB
CD
двух
Построить:
скрещивающихся
: AB , CD║α
прямых проходит Доказать: α - единственная
плоскость,
параллельная
С
другой плоскости,
В
и притом только
А
одна.
D
α

9.

⋁
Аксиомы взаимного расположения точек, прямых и
плоскостей.
Аксиомы наложения и равенства.
Аксиомы измерения отрезков.
⋁
Аксиома параллельных.

10.

1.1. На каждой прямой и в каждой плоскости
имеются точки.
1.2. Имеются по крайней мере три точки, не
лежащие на одной прямой, и по крайней мере
четыре точки, не лежащие в одной плоскости.
1.3. Через любые две точки проходит прямая, и
притом только одна.
1.4. Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и притом
только одна.
1.5. Если две точки прямой принадлежат
плоскости, то и все точки прямой лежат в этой
плоскости.

11.

1.6. Если две плоскости имеют общую точку, то они имеют общую
прямую, на которой лежат все общие точки этих плоскостей.
1.7. Из трех точек прямой одна и только одна лежит между двумя
другими.
1.8. Каждая точка прямой разделяет ее на две части (два луча) так,
что любые две точки одного и того же луча лежат по одну сторону
от данной точки, а любые две точки разных лучей лежат по разные
стороны от данной точки.
1.9. Каждая прямая, лежащая в плоскости, разделяет эту плоскость
на две части (две полуплоскости) так, что любые две точки одной и
той же полуплоскости лежат по одну сторону от данной прямой, а
любые две точки разных полуплоскостей лежат по разные стороны
от данной прямой.
1.10. Каждая плоскость разделяет пространство на две части (два
полупространства) так, что две точки одного и того же
полупространства лежат по одну сторону от данной плоскости, а
любые две точки разных полупространств лежат по разные
стороны от данной плоскости.

12.

13.

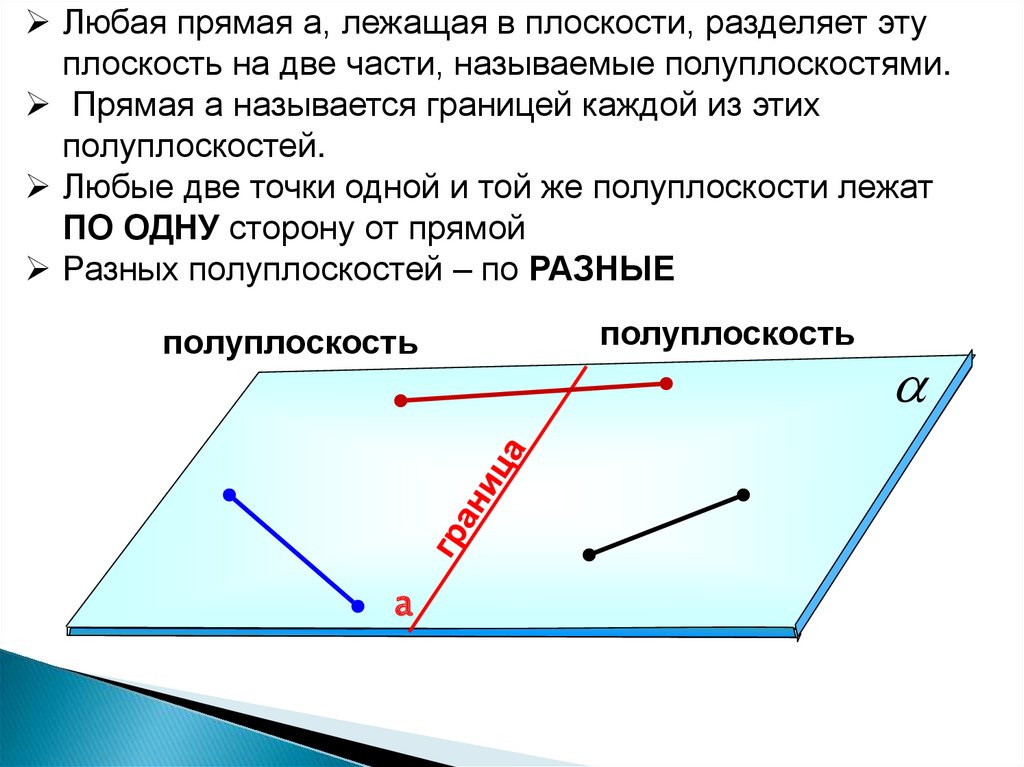
Любая прямая а, лежащая в плоскости, разделяет эту
плоскость на две части, называемые полуплоскостями.
Прямая а называется границей каждой из этих
полуплоскостей.
Любые две точки одной и той же полуплоскости лежат
ПО ОДНУ сторону от прямой
Разных полуплоскостей – по РАЗНЫЕ
полуплоскость
а
полуплоскость

14.

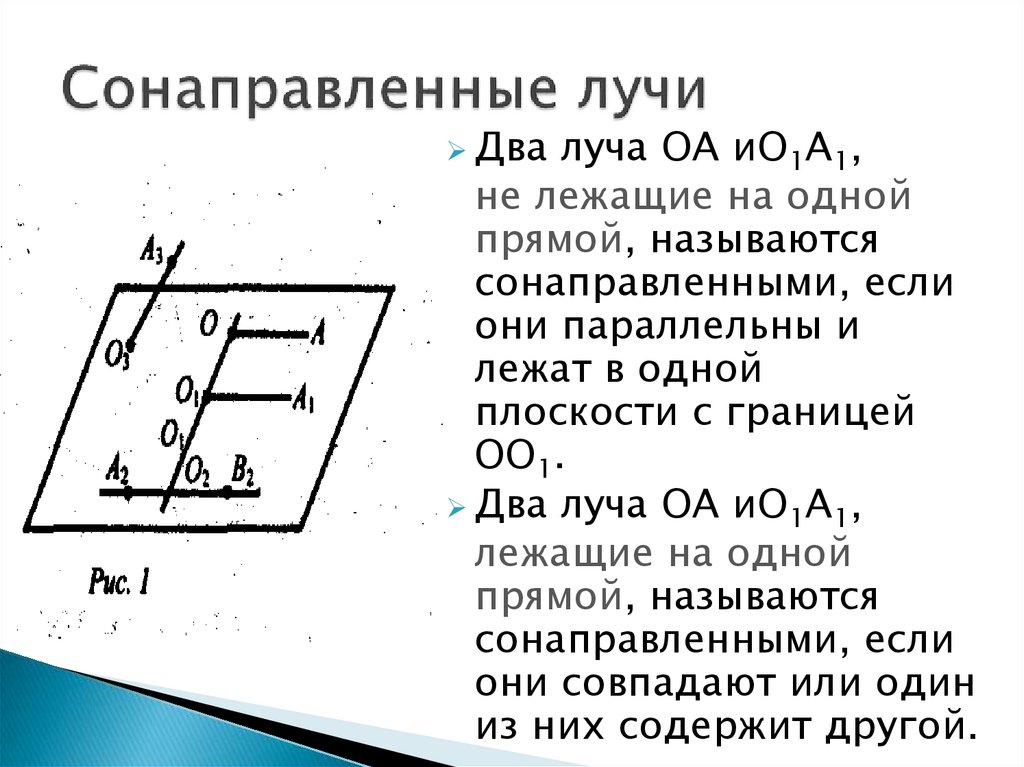
Два
луча ОА иО1А1,
не лежащие на одной
прямой, называются
сонаправленными, если
они параллельны и
лежат в одной
плоскости с границей
ОО1.
Два луча ОА иО1А1,
лежащие на одной
прямой, называются
сонаправленными, если
они совпадают или один
из них содержит другой.

15.

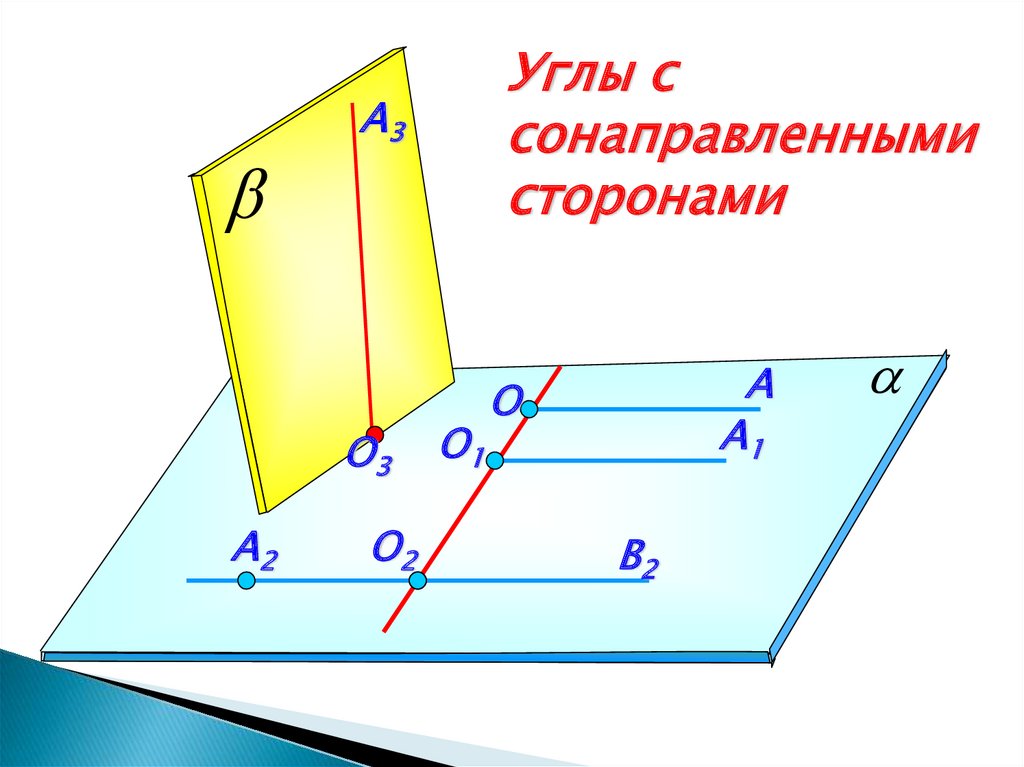
A3
О3
A2
Углы с
сонаправленными
сторонами
О2
О1
A
A1
О
В2

16.

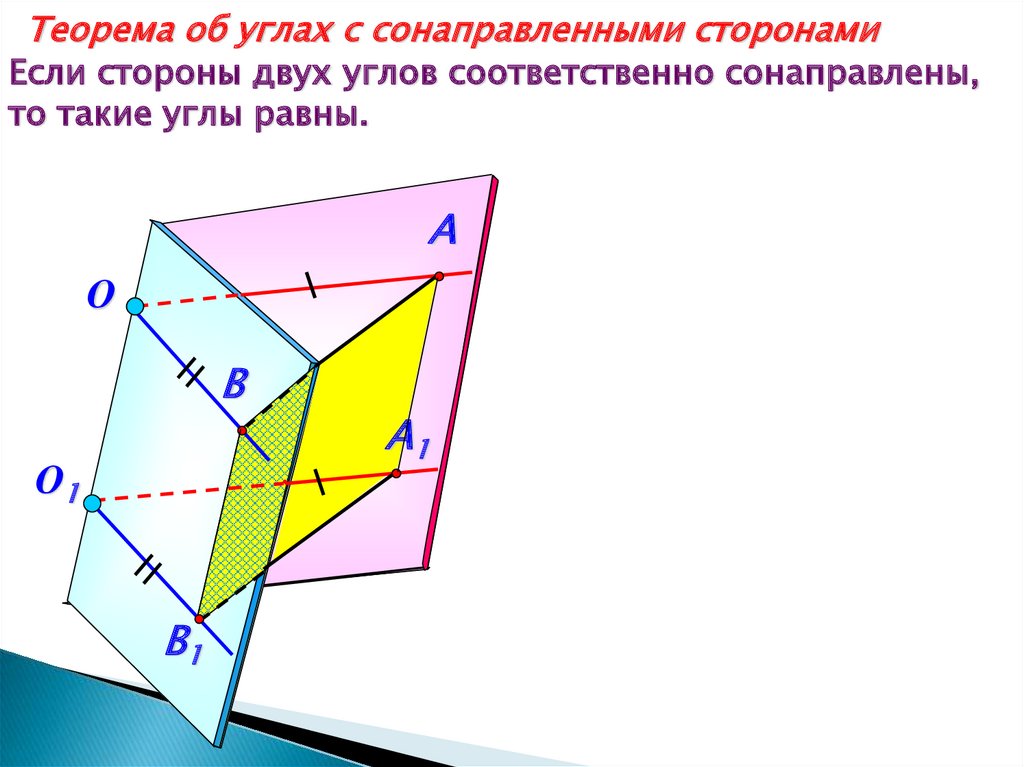
Теорема об углах с сонаправленными сторонами
Если стороны двух углов соответственно сонаправлены,
то такие углы равны.
A
О
B
О1
B1
A1

17.

18.

19.

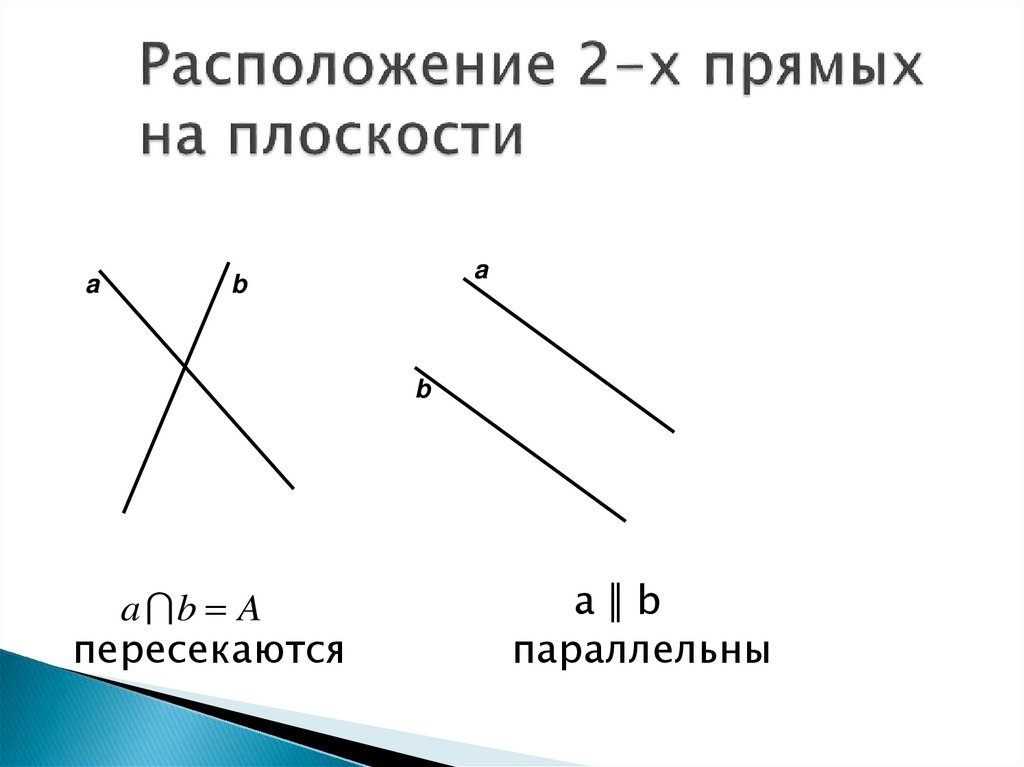
Как могут быть расположены прямые в
пространстве?
Прямые в пространстве могут быть
пересекающимися, параллельными,
скрещивающимися.
Какие прямые в пространстве называются
параллельными?
Две прямые в пространстве называются
параллельными, если они лежат в одной
плоскости и не пересекаются.

20.

a
a
b
b
a b A
пересекаются
а║b
параллельны

21.

22.

Верно ли утверждение: если две прямые не
имеют общих точек, то они не пересекаются
Да, они параллельны или скрещиваются
Точка М не лежит на прямой а. Сколько
прямых, не пересекающих прямую а, проходит
через точку М? Сколько из них параллельны
прямой а?
Бесконечно много. Одна
Каким может быть взаимное расположение двух
прямых, одна из которых лежит в плоскости, а
другая параллельна этой плоскости?
Параллельны или скрещиваются

23.

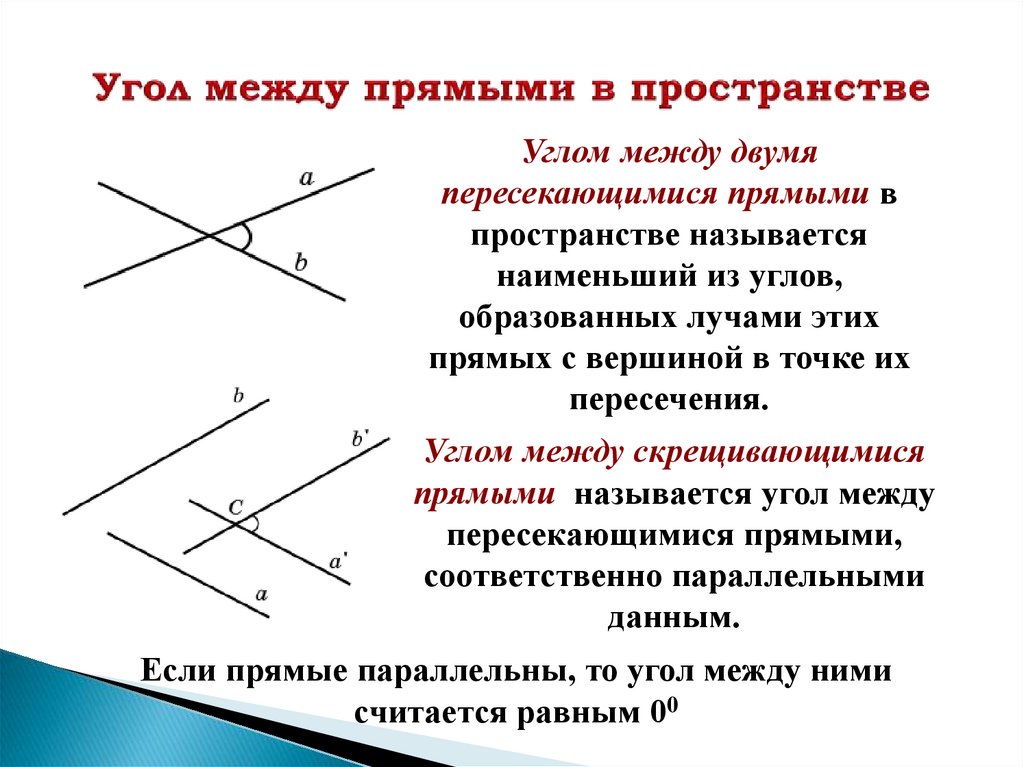
Углом между двумя
пересекающимися прямыми в
пространстве называется
наименьший из углов,
образованных лучами этих
прямых с вершиной в точке их
пересечения.
Углом между скрещивающимися
прямыми называется угол между
пересекающимися прямыми,
соответственно параллельными
данным.
Если прямые параллельны, то угол между ними
считается равным 00

24.

Угол между прямыми – это градусная мера,
а не геометрическая фигура.
Угол между скрещивающимися прямыми АВ
и CD определяется как угол между
пересекающимися прямыми А1В1║АВ и
C1D1║CD (от выбора точки М1 или М2
величина угла φ не зависит)

25.

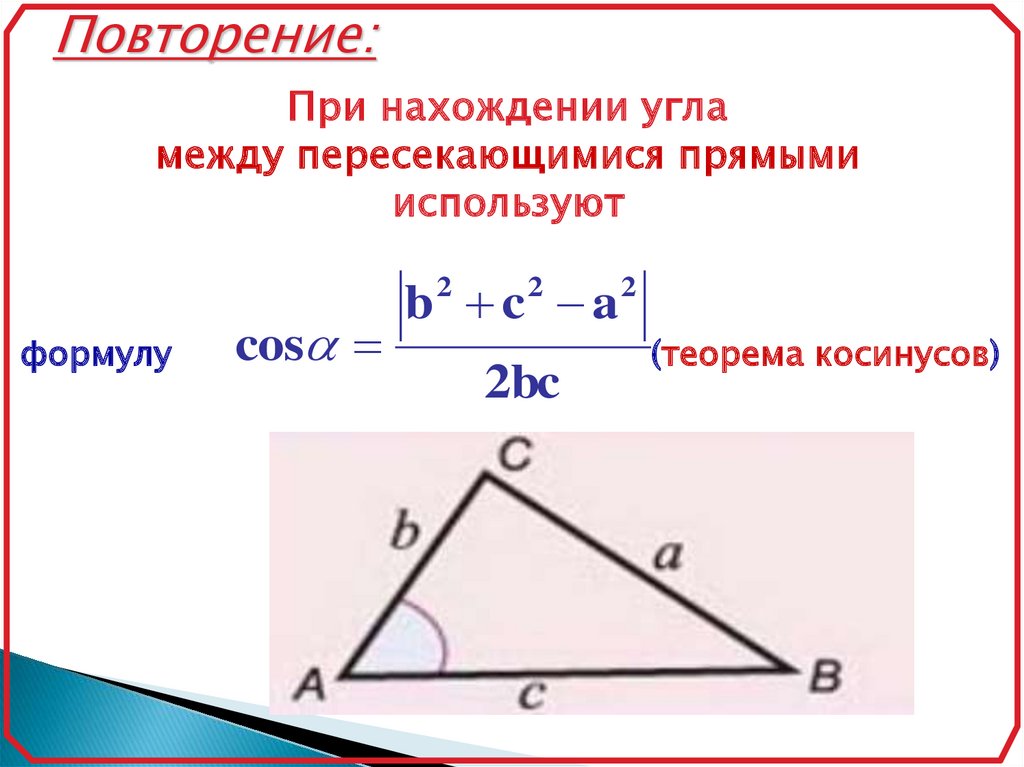
Повторение:
При нахождении угла
между пересекающимися прямыми
используют
b c a
2
формулу
cos
2
2bc
2
(теорема косинусов)

26.

27.

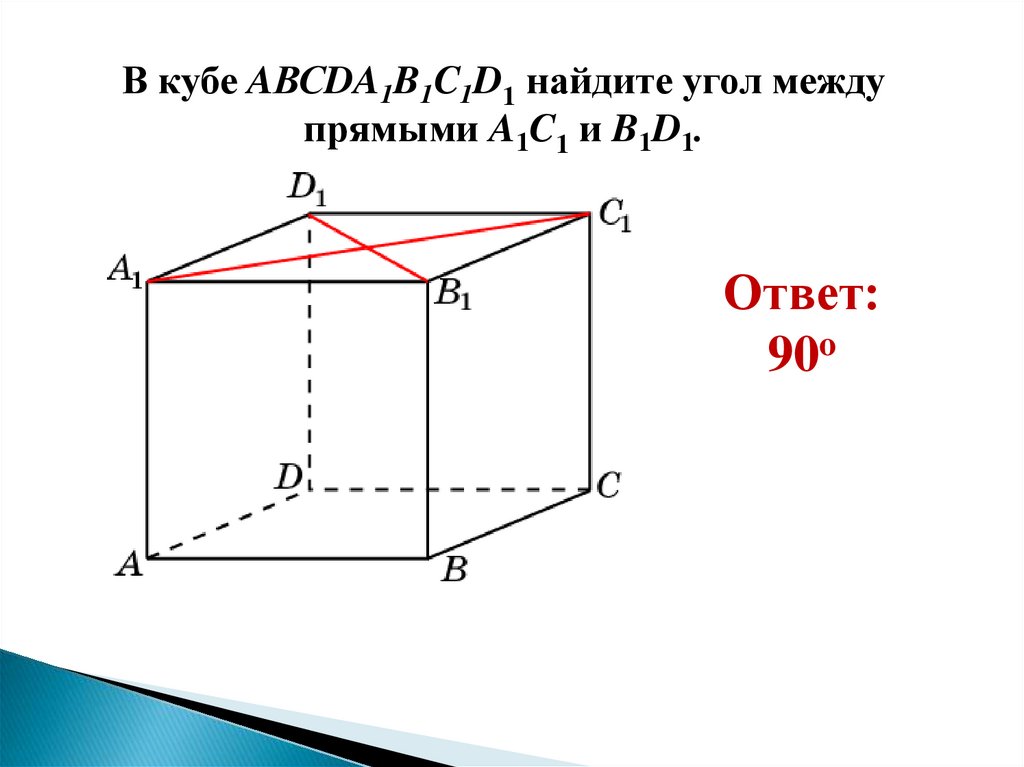
В кубе AВСDA1B1C1D1 найдите угол между
прямыми A1C1 и B1D1.
Ответ:
90o

28.

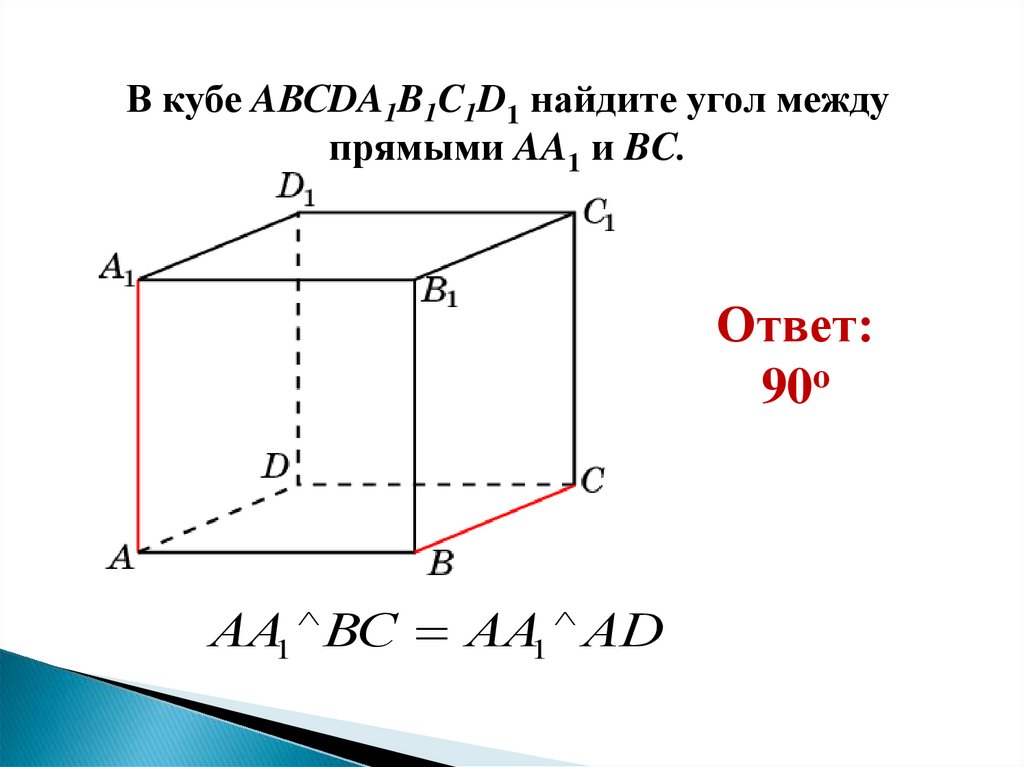
В кубе AВСDA1B1C1D1 найдите угол между
прямыми AA1 и BC.
Ответ:
90o
АА1 ВС АА1 АD

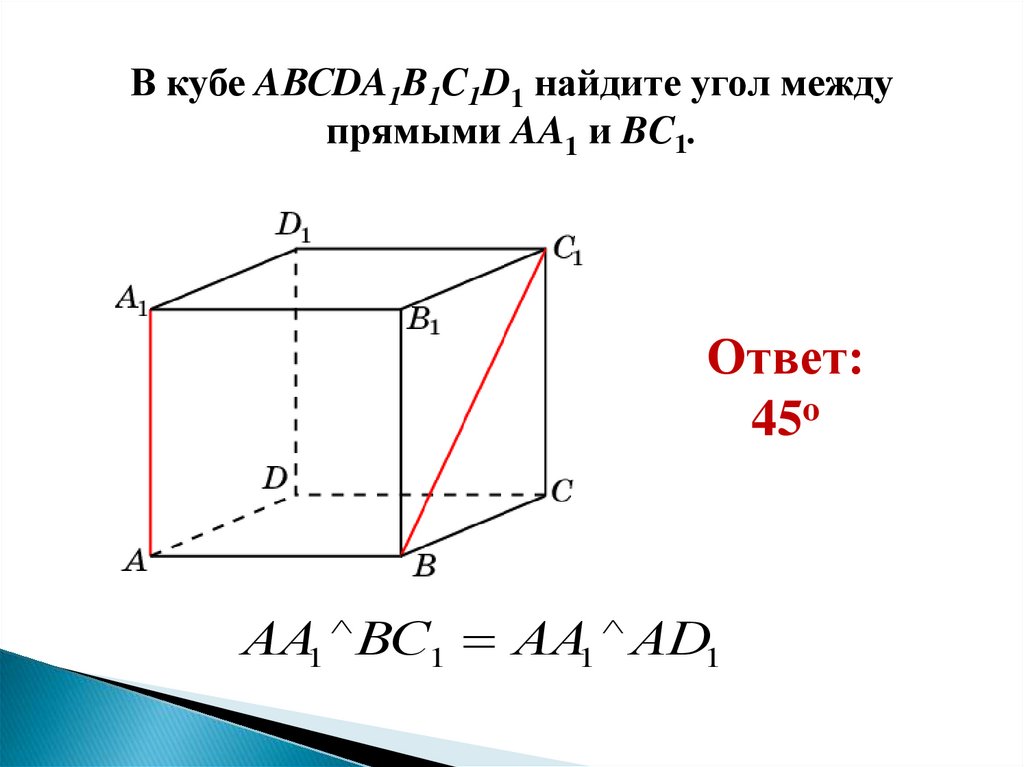
29.

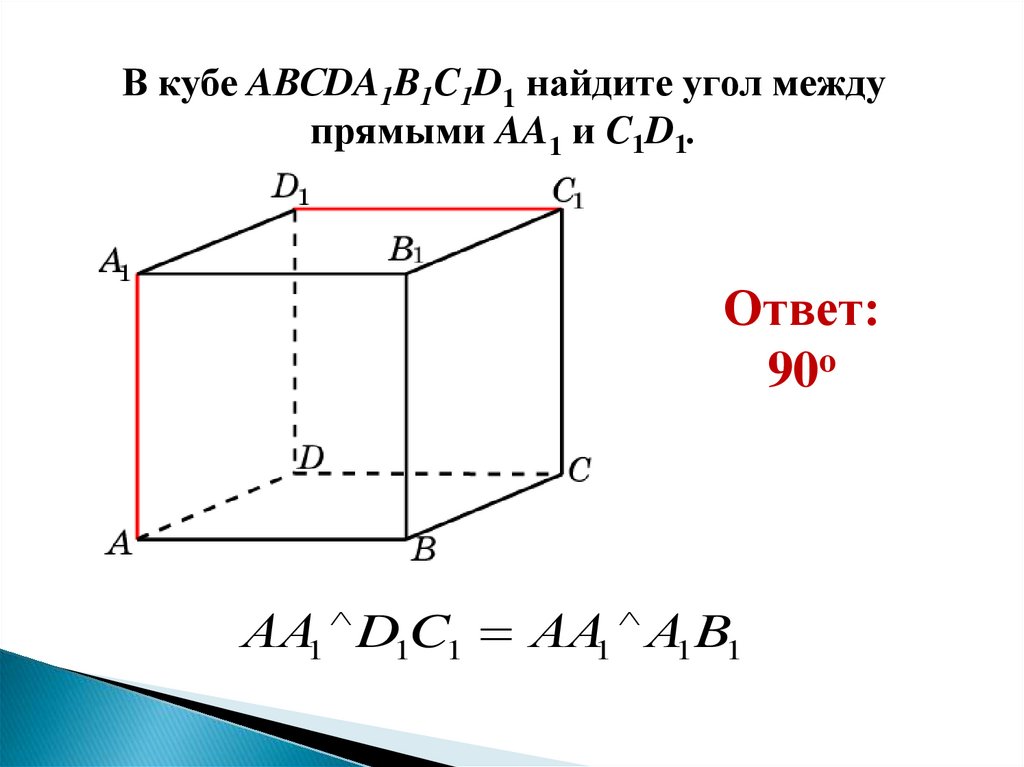
В кубе AВСDA1B1C1D1 найдите угол между
прямыми AA1 и C1D1.
Ответ:
90o
АА1 D1C1 АА1 А1 B1

30.

В кубе AВСDA1B1C1D1 найдите угол между
прямыми AA1 и BC1.
Ответ:
45o
АА1 ВС1 АА1 АD1

31.

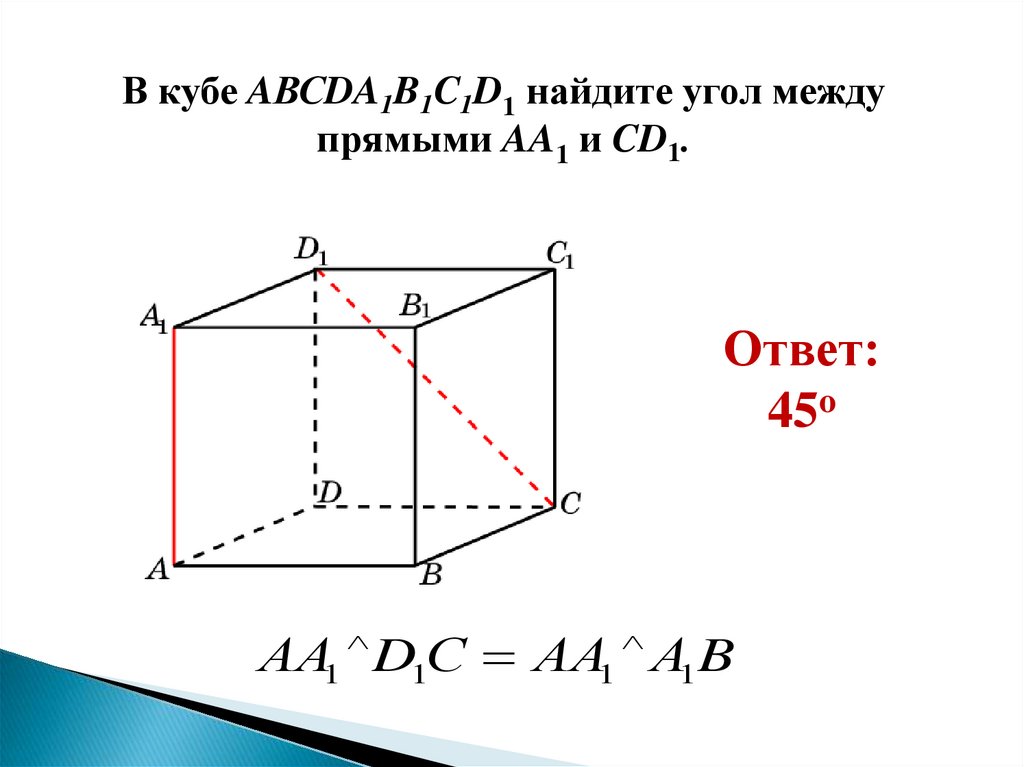
В кубе AВСDA1B1C1D1 найдите угол между
прямыми AA1 и CD1.
Ответ:
45o
АА1 D1С АА1 А1 B

32.

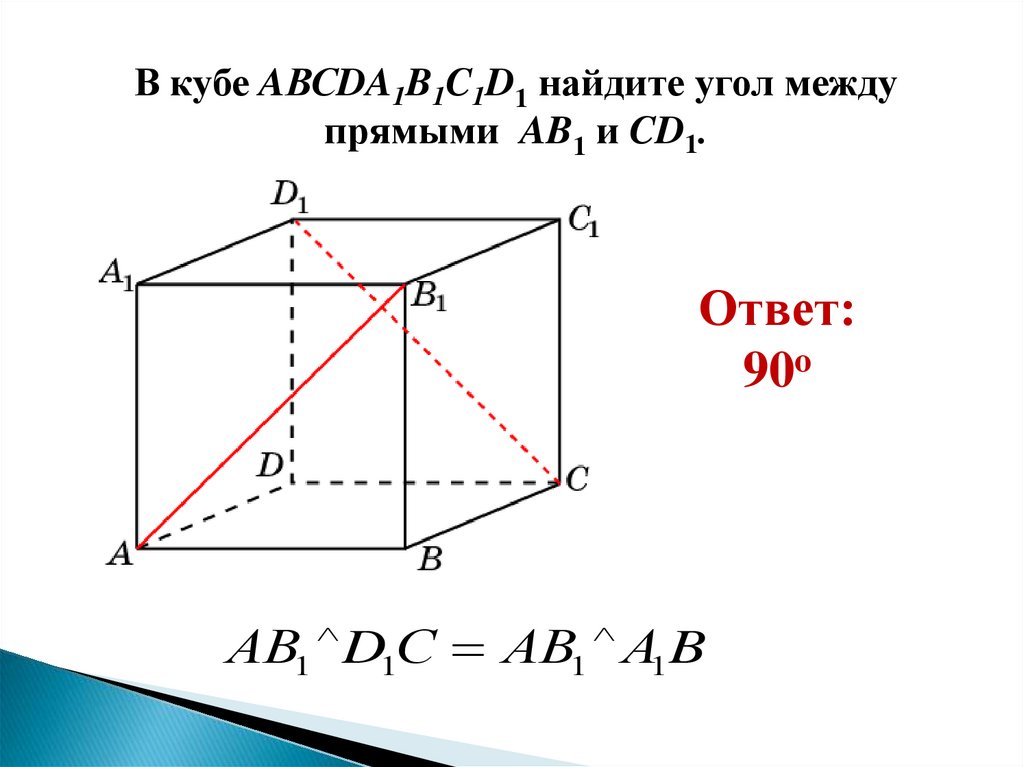
В кубе AВСDA1B1C1D1 найдите угол между
прямыми AB1 и CD1.
Ответ:
90o
АВ1 D1С АВ1 А1 B

33.

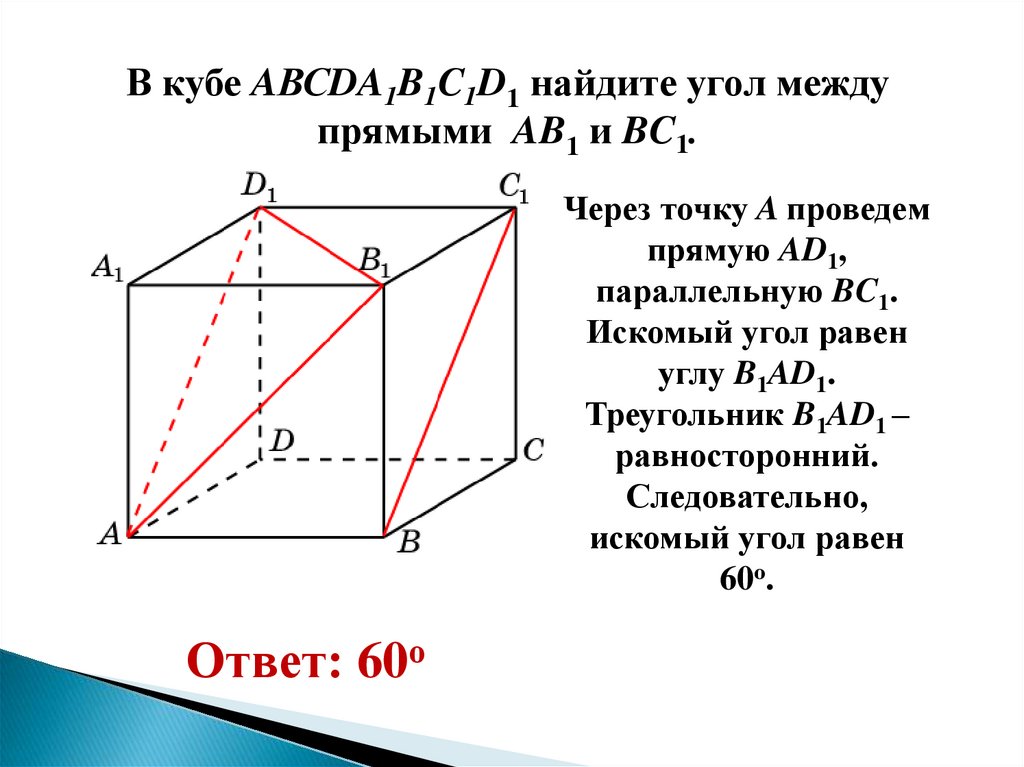
В кубе AВСDA1B1C1D1 найдите угол между
прямыми AB1 и BC1.
Через точку A проведем
прямую AD1,
параллельную BC1.
Искомый угол равен
углу B1AD1.
Треугольник B1AD1 –
равносторонний.
Следовательно,
искомый угол равен
60о.
Ответ: 60о

34.

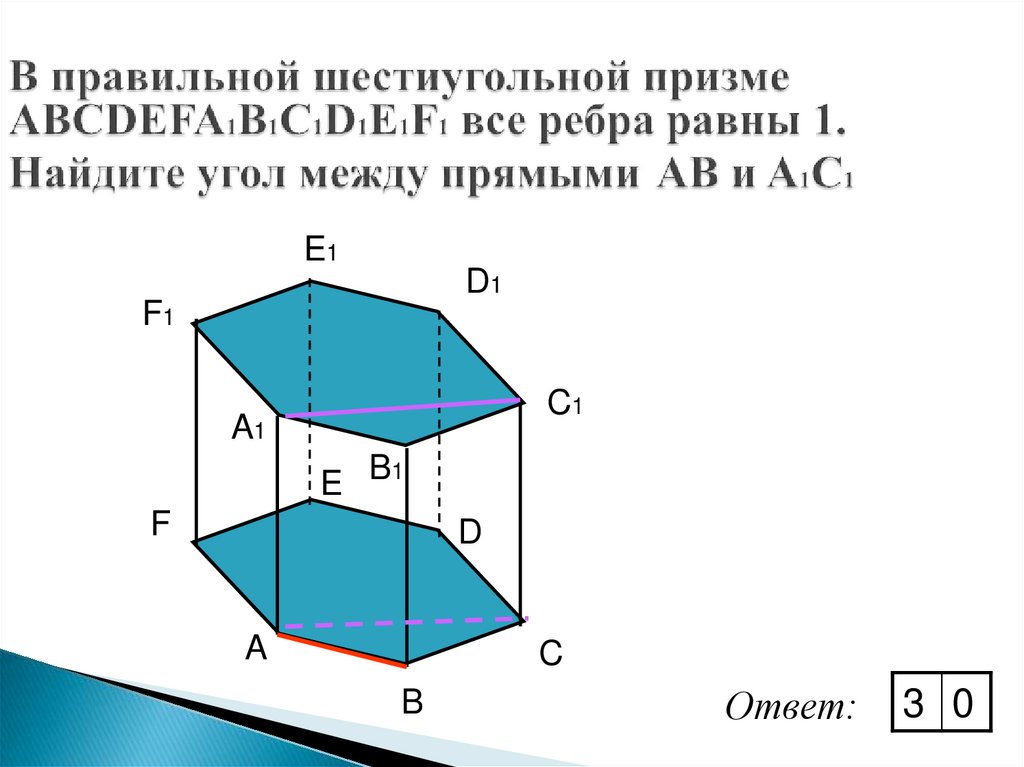
E1
D1
F1
C1
A1
E B1
F
D
A
C
B
Ответ:
3 0

35.

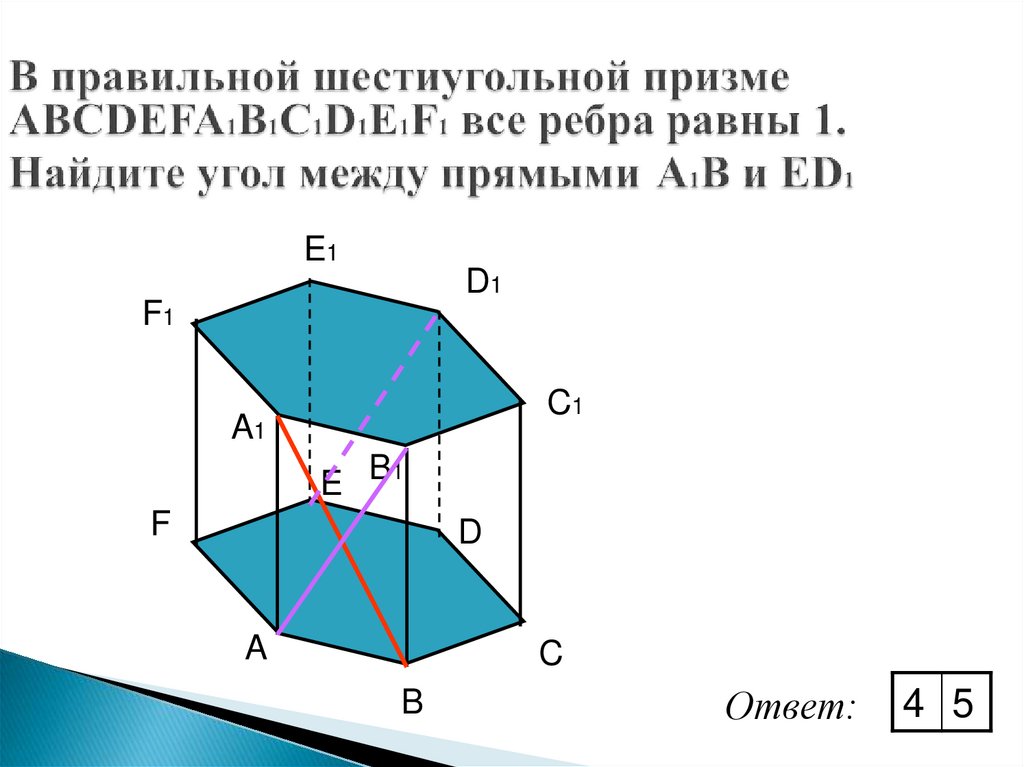
E1
D1
F1
C1
A1
E B1
F
D
A
C
B
Ответ:
4 5

36.

37.

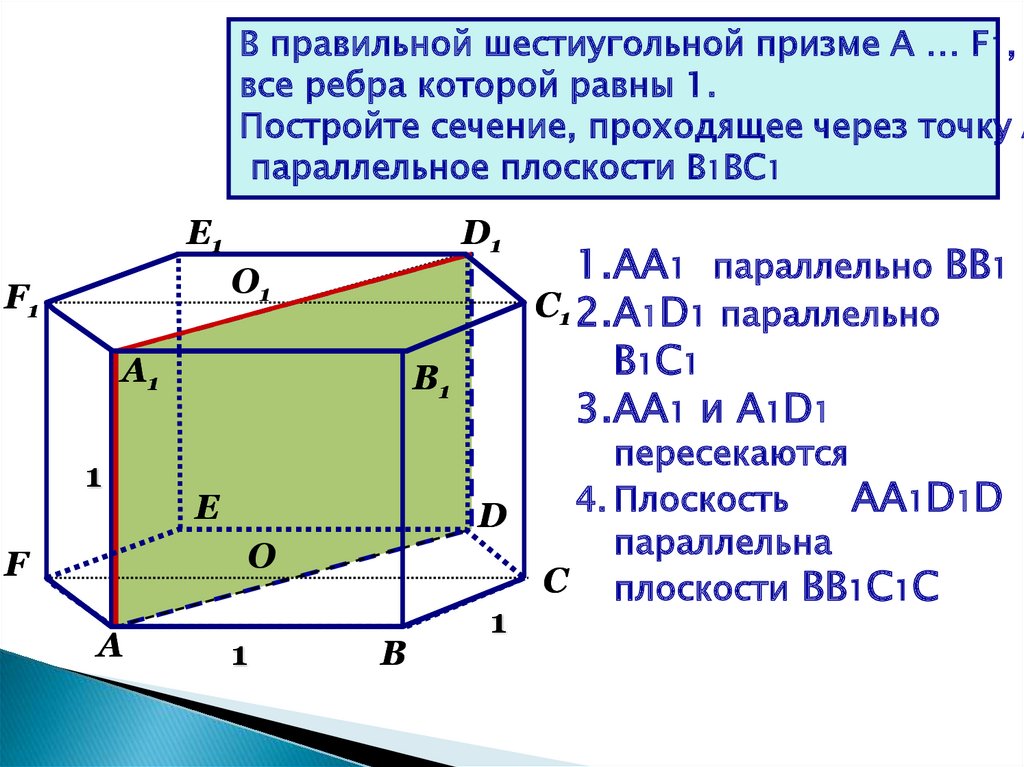
В правильной шестиугольной призме A … F1,
все ребра которой равны 1.
Постройте сечение, проходящее через точку А
параллельное плоскости В1ВС1
Е1
D1
О1
F1
А1
1
В1
Е
D
О
F
А
1
В
1
1.АА1 параллельно ВВ1
С1 2.А1D1 параллельно
В1С1
3.АА1 и A1D1
пересекаются
4. Плоскость
АА1D1D
параллельна
С плоскости ВВ1С1С

38.

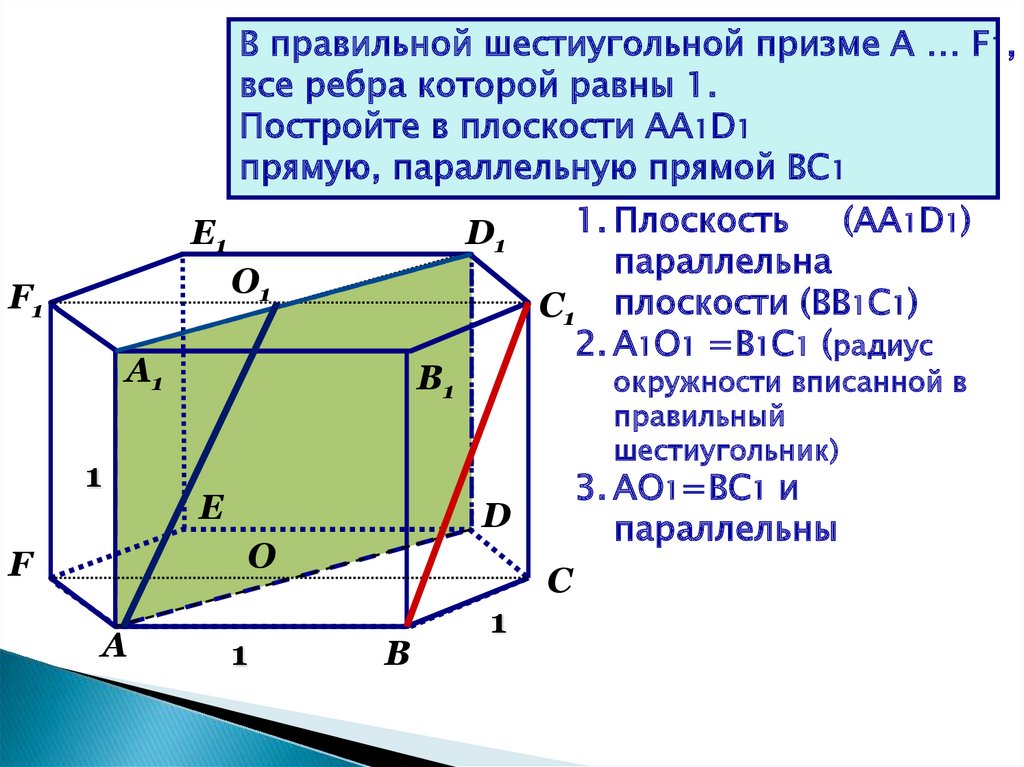
В правильной шестиугольной призме A … F1,
все ребра которой равны 1.
Постройте в плоскости АА1D1
прямую, параллельную прямой ВС1
Е1
D1
О1
F1
А1
1
В1
Е
окружности вписанной в
правильный
шестиугольник)
А
3. АО1=ВС1 и
параллельны
D
О
F
1. Плоскость
(АА1D1)
параллельна
С1 плоскости (ВВ1С1)
2. А1О1 =В1С1 (радиус
1
С
В
1

39.

В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1,
все ребра которой равны 1,
найдите косинус угла
между прямыми
AB1 и BC1

40.

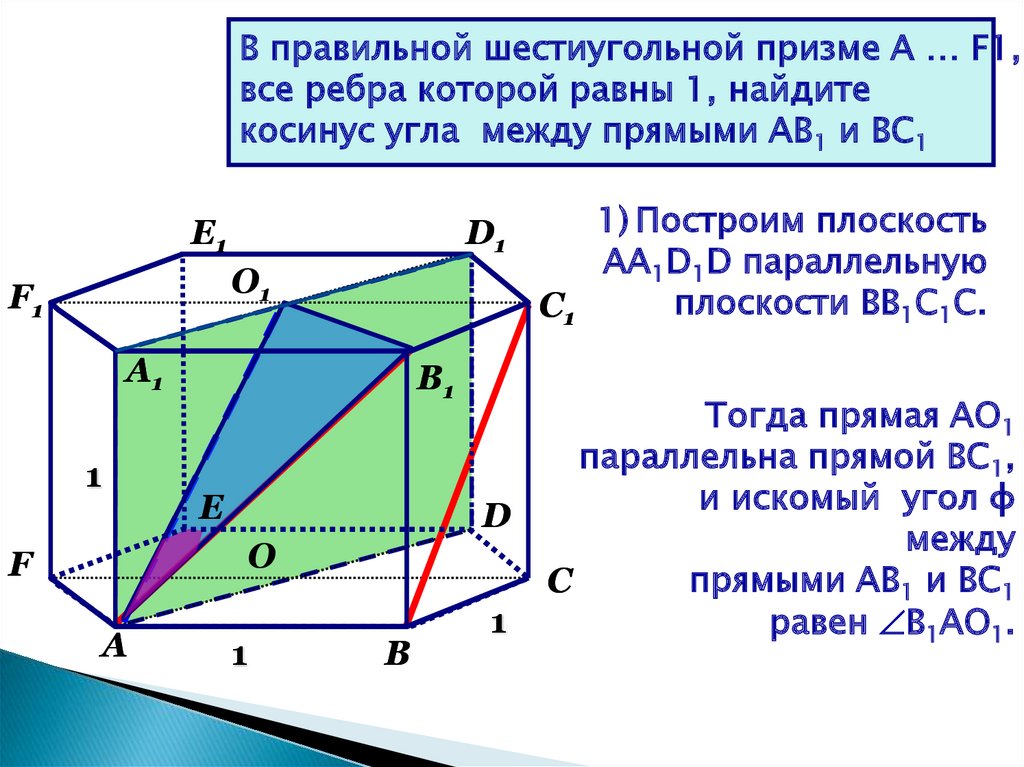
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите
косинус угла между прямыми AB1 и BC1
Е1
D1
О1
F1
А1
1
В1
Е
D
О
F
А
1
В
1
1) Построим плоскость
АА1D1D параллельную
плоскости ВВ1С1С.
С1
Тогда прямая AO1
параллельна прямой BC1,
и искомый угол φ
между
прямыми AB1 и BC1
С
равен B1AO1.

41.

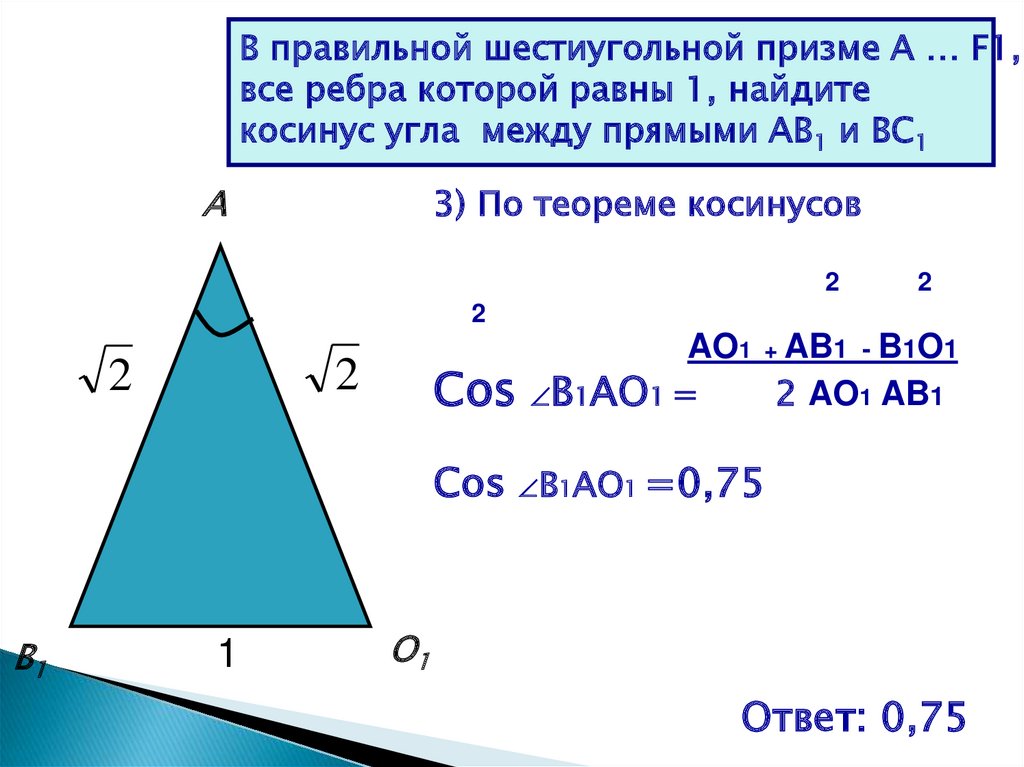
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите
косинус угла между прямыми AB1 и BC1
А
3) По теореме косинусов
2
2
2
Cos
2
2
AO1 + AB1 - B1O1
B1AO1 =
2 AO1 AB1
2
Cos B1AO1 =0,75
В1
1
О1
Ответ: 0,75

42.

43.

С помощью параллельного переноса
№1
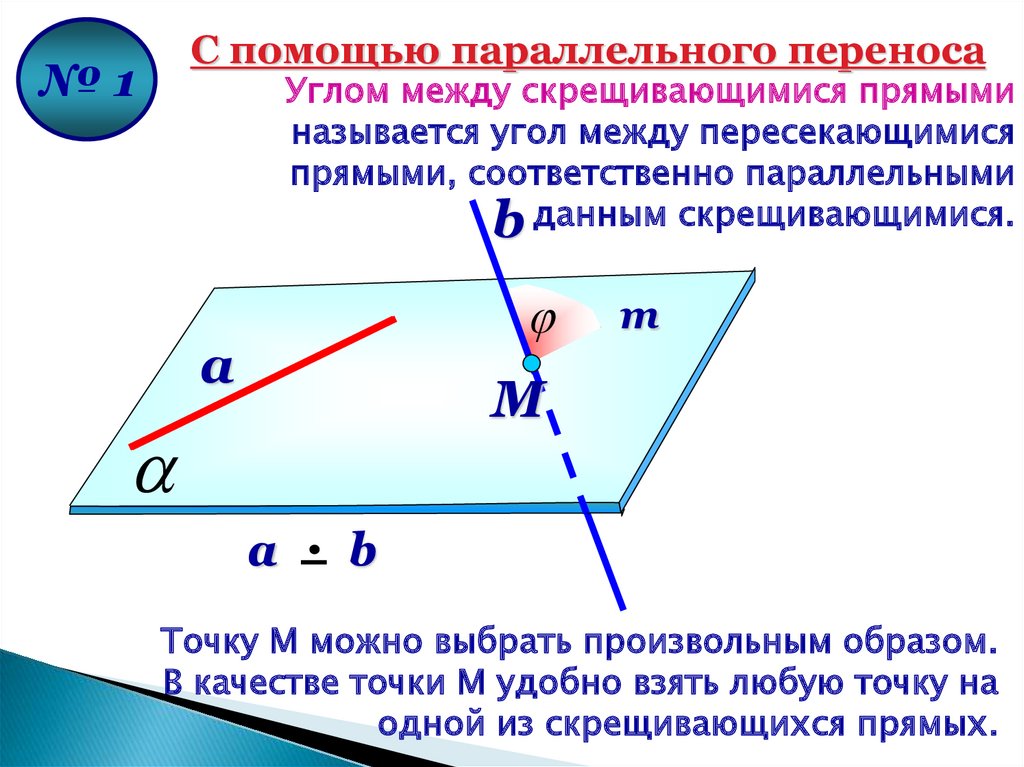
Углом между скрещивающимися прямыми
называется угол между пересекающимися
прямыми, соответственно параллельными
b данным скрещивающимися.
a
m
M
a
b
Точку М можно выбрать произвольным образом.
В качестве точки М удобно взять любую точку на
одной из скрещивающихся прямых.

44.

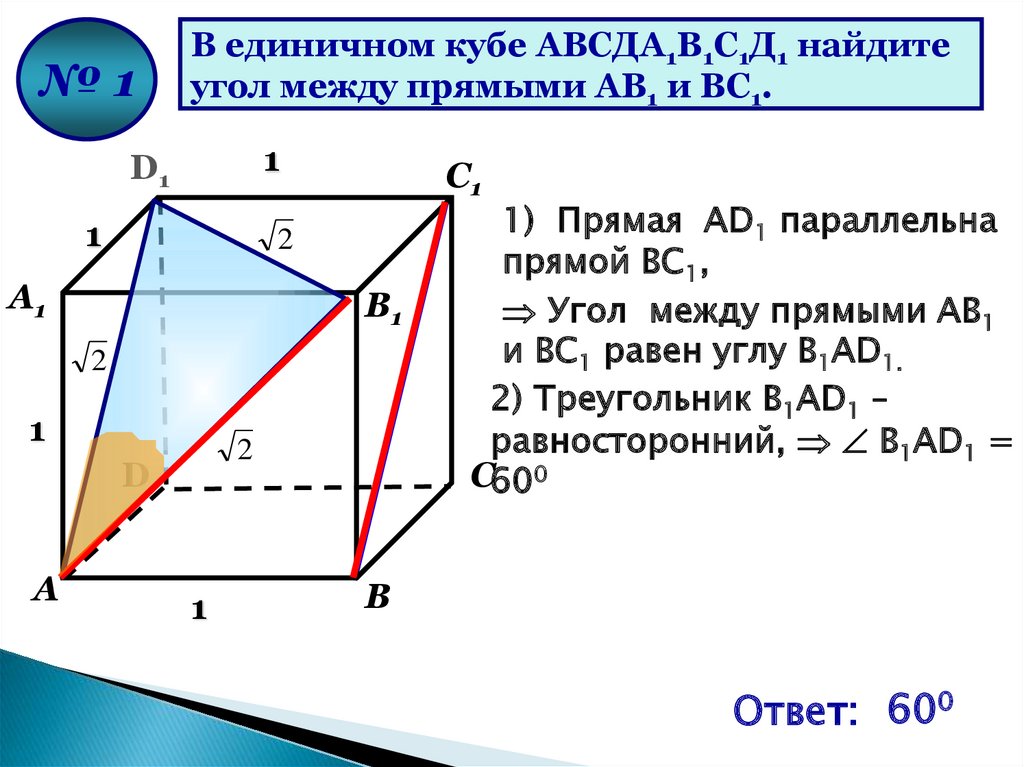
№1
В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми АВ1 и ВС1.
1
D1
1
С1
2
А1
В1
2
1
2
D
А
1
1) Прямая AD1 параллельна
прямой ВС1,
Угол между прямыми АВ1
и ВС1 равен углу В1AD1.
2) Треугольник В1AD1 –
равносторонний, В1AD1 =
С600
В
Ответ: 600

45.

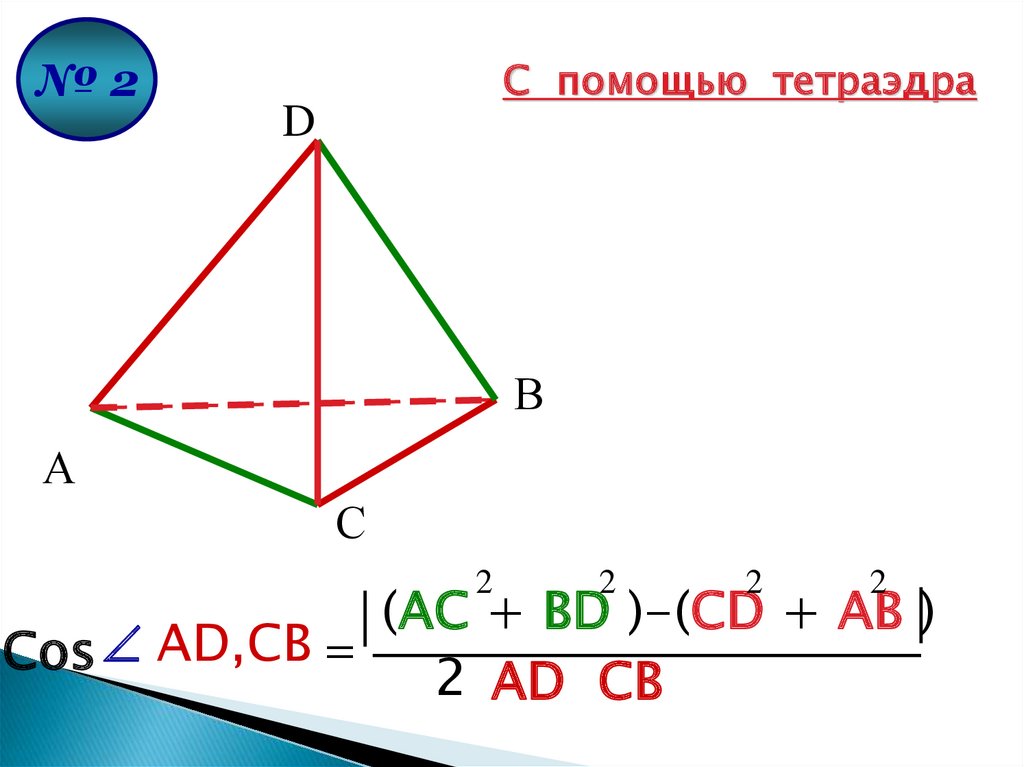
№2
С помощью тетраэдра
D
В
А
С
2
2
2
2
(AC + BD )-(CD + AB )
Cos AD,CB
2 AD CB

46.

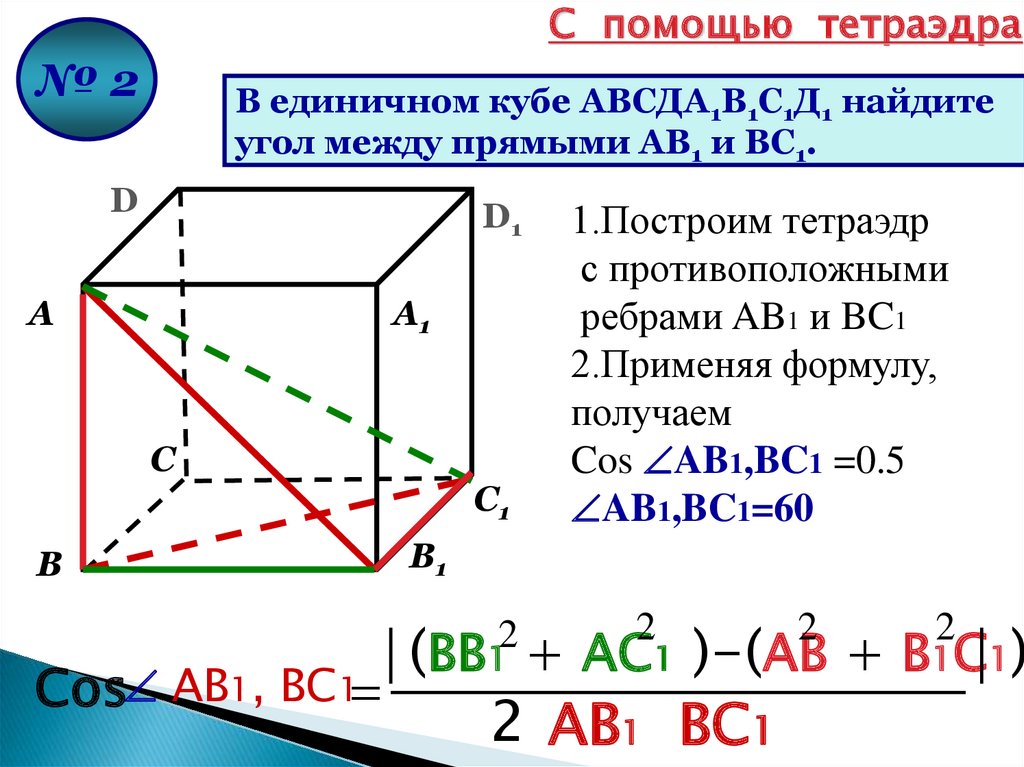
С помощью тетраэдра
№2
В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми АВ1 и ВС1.
D
D1
А
А1
С
С1
В
1.Построим тетраэдр
с противоположными
ребрами AB1 и BC1
2.Применяя формулу,
получаем
Cos AB1,BC1 =0.5
AB1,BC1=60
В1
(BB1 + AC1 )-(AB + B1C1)
Cos AB1, BC1
2 AB1 BC1
2
2
2
2

47.

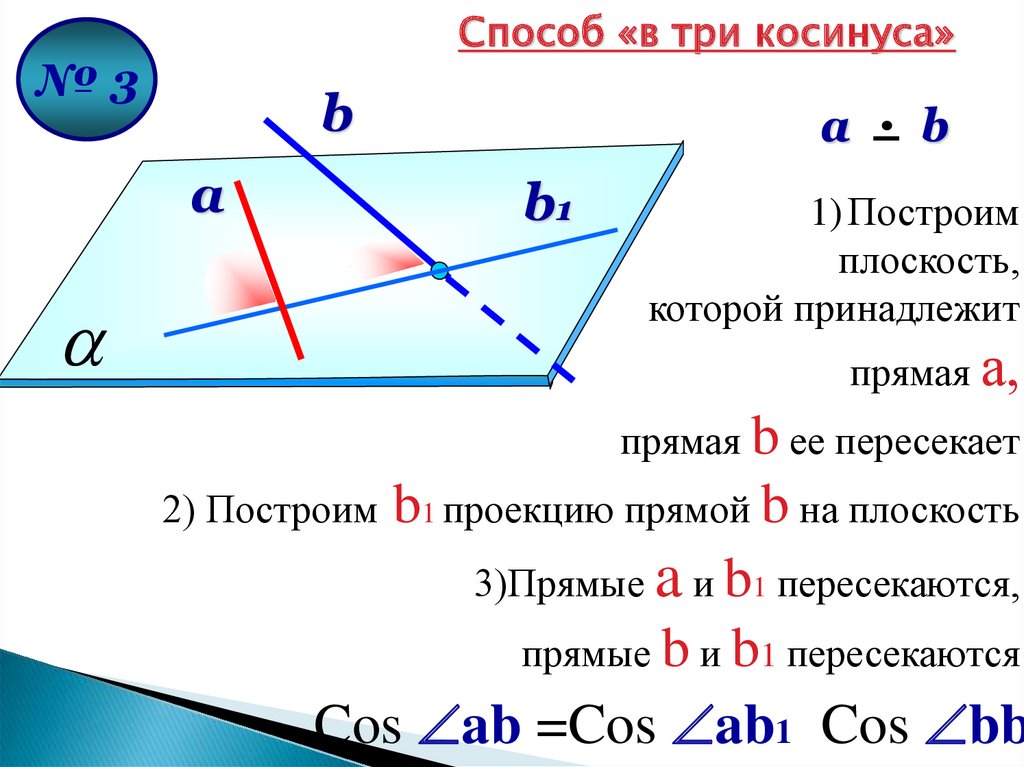
Способ «в три косинуса»
№3
b
a
a
b1
b
1) Построим
плоскость,
которой принадлежит
прямая а,
прямая b ее пересекает
b1 проекцию прямой b на плоскость
3)Прямые a и b1 пересекаются,
прямые b и b1 пересекаются
Cos ab =Cos ab1 Cos bb
2) Построим

48.

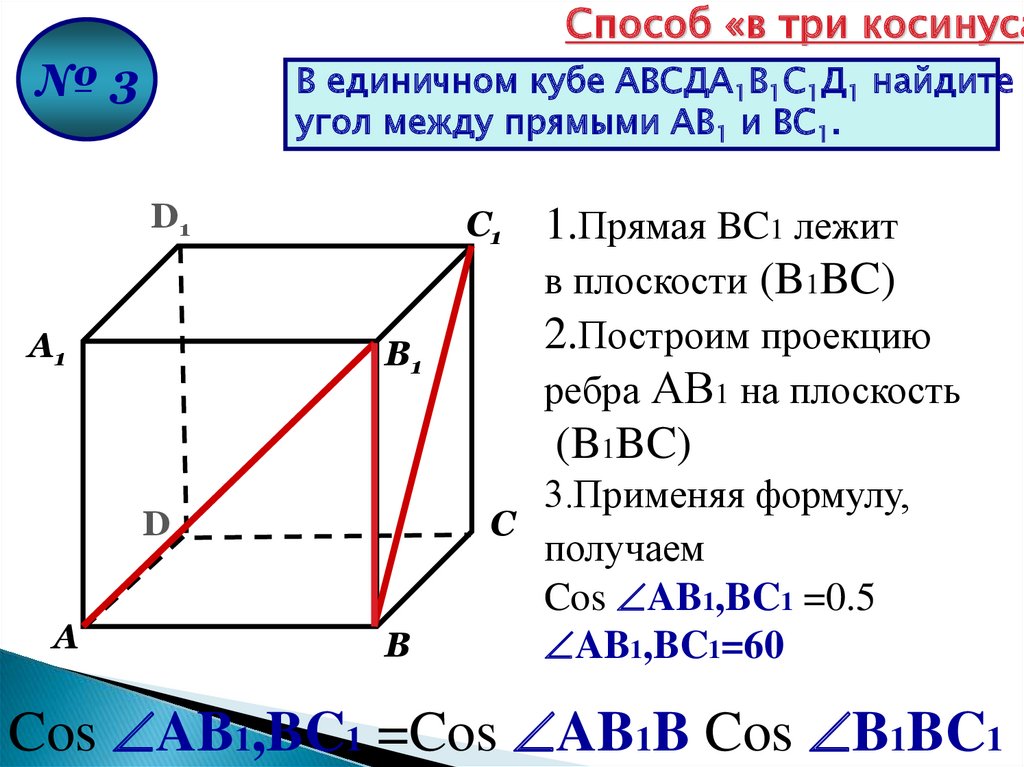
Способ «в три косинуса
№3
В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми АВ1 и ВС1.
D1
А1
С1
В1
D
А
В
1.Прямая BC1 лежит
в плоскости (B1BC)
2.Построим проекцию
ребра АВ1 на плоскость
(B1BC)
3.Применяя формулу,
С
получаем
Cos AB1,BC1 =0.5
AB1,BC1=60
Cos AB1,BC1 =Cos AB1B Cos B1BC1

49.

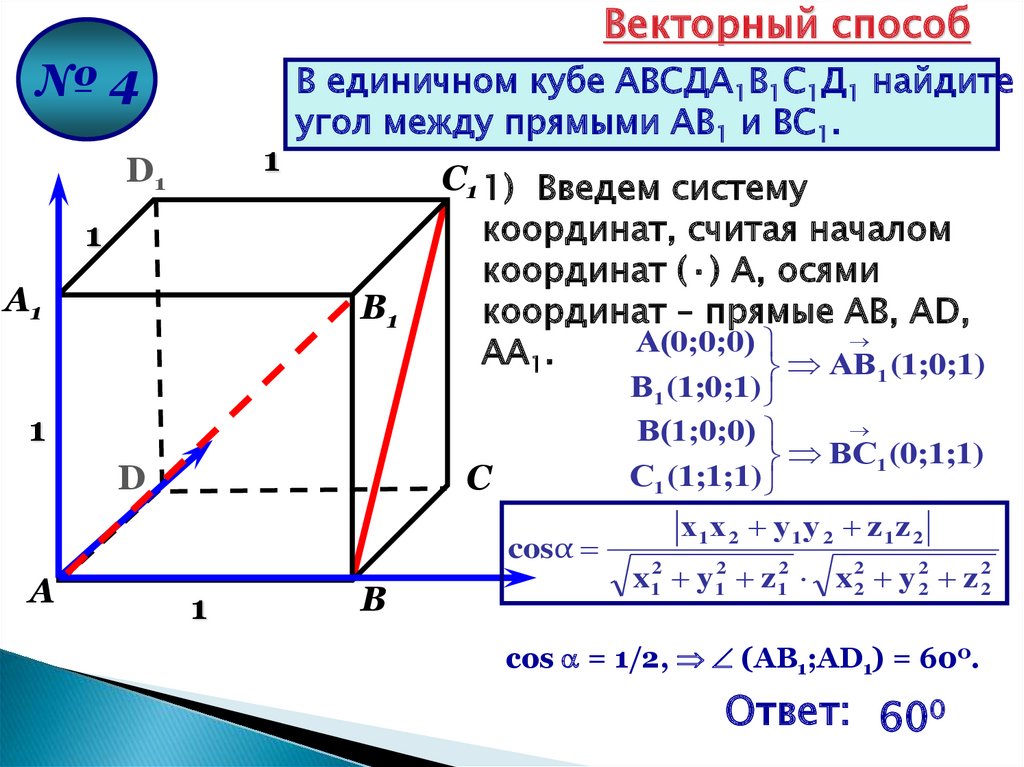
Векторный способ
№4
1
D1
В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми АВ1 и ВС1.
1
А1
В1
С1 1) Введем систему
координат, считая началом
координат (·) А, осями
координат – прямые АВ, АD,
А(0;0;0)
АА1.
АВ (1;0;1)
1
В1 (1;0;1)
В(1;0;0)
ВС1 (0;1;1)
С1 (1;1;1)
1
D
С
cosα
А
1
В
х1 х 2 у 1 у 2 z 1 z 2
x12 y 12 z 12 x 22 y 22 z 22
cos = 1/2, (АВ1;AD1) = 600.
Ответ: 600