Похожие презентации:
Неопределенный интеграл Ч2, свойства неопределенного интеграла
1.
2.
Неопределенныминтегралом
от
непрерывной
функции
f(x)
на
интервале (a; b) называют любую ее
первообразную функцию.
f
(
x
)
dx
F
(
x
)
c
Где С – произвольная постоянная (const).
3.
1. F(x) =Сх+С1.f(x) = хn
2. F(x) =
2.f(x) = C
3. F(x) = tg x+С
3.f(x)=sinx
4.f(x) =
1
2
4. F(x) = sin x+С
sin x
5. F(x) = сtg x+С
5.f(x) =cosx
6.f(x)=
x n 1
С
n 1
1
cos 2 x
6. F(x) = - cos x+С
4.
Свойства интеграла(
f
(
x
)
g
(
x
)
)
dx
f ( x)dx g ( x)dx
Cf
(
x
)
dx
C
f
(
x
)
dx
5.
Свойства интегралаf ( х)dx
f ( х)
f ( x)dx f ( x) С
1
f (kx b)dx F (kx b) C
k
6.
1.Табличный.2.Сведение к табличному
преобразованием подынтегрального
выражения в сумму или разность.
3.Интегрирование с помощью замены
переменной (подстановкой).
4.Интегрирование по частям.
7.
Таблица неопределенныхинтегралов
1. dx x C .
a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
8.
Таблица неопределенныхинтегралов
11.
dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
a x
2
arcsin
2
x
C ..
a
x2 a
ln x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
dx
1
x a
ln
C
2
2
2a x a
x a
19.
dx
1
a x
ln
a 2 x 2 2a a x C .
20.
14.
15.
dx
dx
16.
dx
ch 2 x thx C .
dx
cthx C .
2
sh x
9.
1) f(x) =10х2) f(x) =3 х²
3) f(x) = sinх+5
4) f(x) = 5cosx
5) f(x) = 6х²
6) f(x) = 3-2х
10.
Верно ли что:а)
x
dx
5
x
C
5
4
б)
в)
3
x
dx
x
C
2
3
г)
3
x
dx
6
x
C
2
1 7
x
dx
x
C
7
6
11.
5(
3
x
4 cos x 2 x 1)dx
Интеграл суммы выражений равен сумме
интегралов этих выражений
Постоянный
множитель можно
вынести за знак
интеграла
12.
Пример 2.3
2
4
x
( x 5 x 7e x )dx
Записать
решение:
13.
Пример 3.4
3
(
x
3 х ) dx
cos 2 x
Записать
решение:
14.
sin(6 x 2)dxВведем новую переменную и
выразим дифференциалы:
Записать
решение:
15.
Пример 5.3 6 x dx
Записать
решение:
Проверить
решение
16.
Cамостоятельная работаНайти неопределенный интеграл
Уровень «А» (на «3»)
Проверить
решение
Уровень «В» (на «4»)
1 65 3 2
1
1). (xх 3x х 44x) dxC
6
2
1
54
33.
) (3
(3 4 xx)) dx
C
20
2)5 x 3e 4 ln x C
3
1 66xx 3
4). e
dx
4
e
C
6
4
4
х
5
x
2. ( 25 х 3е ) dx
х
Уровень «С» (на «5»)
1
22
3 6
5
sin(55xx 44
) ) dx
C 66.)2 ctgx
( 2 x xx 3х5 )dx
C
5). cos(
5
sin 3x
5x
17.
ЗаданиеУстановить соответствие. Найти такой общий вид
первообразной, которая соответствует заданной
функции.
x
1. F x cos x C
2
3
1. f x x x
x2
x4
2. F ( x )
C
2
4
2. f x 2 cos x
5 x 2 10 x 3
3.F ( x ) 8 x
C
2
3
2
4. F ( x ) 2 sin x C
3. f x 8 5 x 10 x
4. f x 4 3 x
9
10 x 2
5.F ( x ) 8 x sin x
C
3
1
10
6. F ( x )
4
3
x
C
30
1
10
7. F ( x ) 4 3 x C
3
18.
Основные методы вычислениянеопределенных интегралов
При сведении данного интеграла к
табличному часто используется следующее
преобразование дифференциала (операция
«подведения под знак дифференциала»).
f ( x )dx d ( f ( x ))
Например: dx d ( x b ),
b const;
1
dx d (ax b ), a 0, a const;
a
b const;
cos xdu d (sin x ).
19.
Примеры1
9
1. (3 x 1) dx (3 x 1) d (3 x 1)
3
10
1 (3 x 1)
C.
3
10
9
dx
1 d (4 x 5) 1
2.
ln 4 x 5 C .
4
4x 5 4 4x 5
x
x
x
3. cos 7 dx 5 cos 7 d 7
5
5
5
x
5sin 7 C .
5
20.
Интегрирование заменой переменнойМетод замены переменной (метод
подстановки) состоит в преобразовании
интеграла f(x)dx
в другой интеграл
f(t)dt ,
который вычисляется проще, чем исходный.
21.
Пример(6
x
3)
dx
t 6x 3
dt
dt 6dx , dx
6
6
1 5
1t
t dt
C ( t 6 x 3)
6
66
1.
5
1
6
(6 x 3) C .
36
22.
t 5 7xdx
2.
1
5 7 x dt 7dx , dx dt
7
1 dt
1
ln t C ( t 5 7 x )
7 t
7
1
ln 5 7 x C .
7
23.
xt 8,
x
2
3. sin 8 dx
1
2
dt dx , dx 2dt
2
x
2 sin tdt 2cos t C ( t 8)
2
x
2cos 8 C .
2
24.
Интегрирование по частямФормула
udv uv vdu,
где u u( x ) и v v ( x ) – дифференцируемые
функции, называется
формулой интегрирования по частям.
Метод
интегрирования
по
частям
целесообразно применять, если
vdu
более прост в вычислении, чем
udv
.
25.
Некоторые типы интегралов, которыеможно вычислять методом интегрирования
по частям
1. Интегралы вида Pn ( x )e mx dx , Pn ( x )a mx dx,
P ( x)sin mxdx, Pn ( x )cos mxdx,
n
где Pn ( x ) − многочлен, m − число.
Здесь полагают u Pn ( x ),
за dv обозначают остальные сомножители.
26.
2. Интегралы вида Pn ( x )ln xdx, Pn ( x )arcsin xdx,P ( x)arccos xdx, P ( x)arctgxdx, P ( x)arcctgxdx.
n
n
n
Pn ( x )dx dv
Здесь полагают
за u обозначают остальные сомножители.
3. Интегралы вида e ax cos bxdx, e ax sin bxdx ,
где a и b − числа.
ax
За u можно принять функцию e .
27.
Пример. Вычислить неопределенныеинтегралы методом интегрирования по
частям.
1. 2 x 5 cos xdx
u 2 x 5, du 2dx
dv cos x , v cos xdx sin x
(2 x 5) sin x 2 sin xdx (2 x 5)sin x 2cos x C
2. x cos xdx
u x, du dx
dv cos xdx, v sin x
=
x sin x sin xdx x sin x cos x C .
28.
u ln x , du3. x ln xdx
dv xdx , v
dx
2
2
x
x dx
x
ln x
2
2
2 x
x
2
x
2
2
2
x
2
ln x
1
2
ln x
x
xdx
2
4
C
x
2
2
ln x
1 x
2
2 2
C


















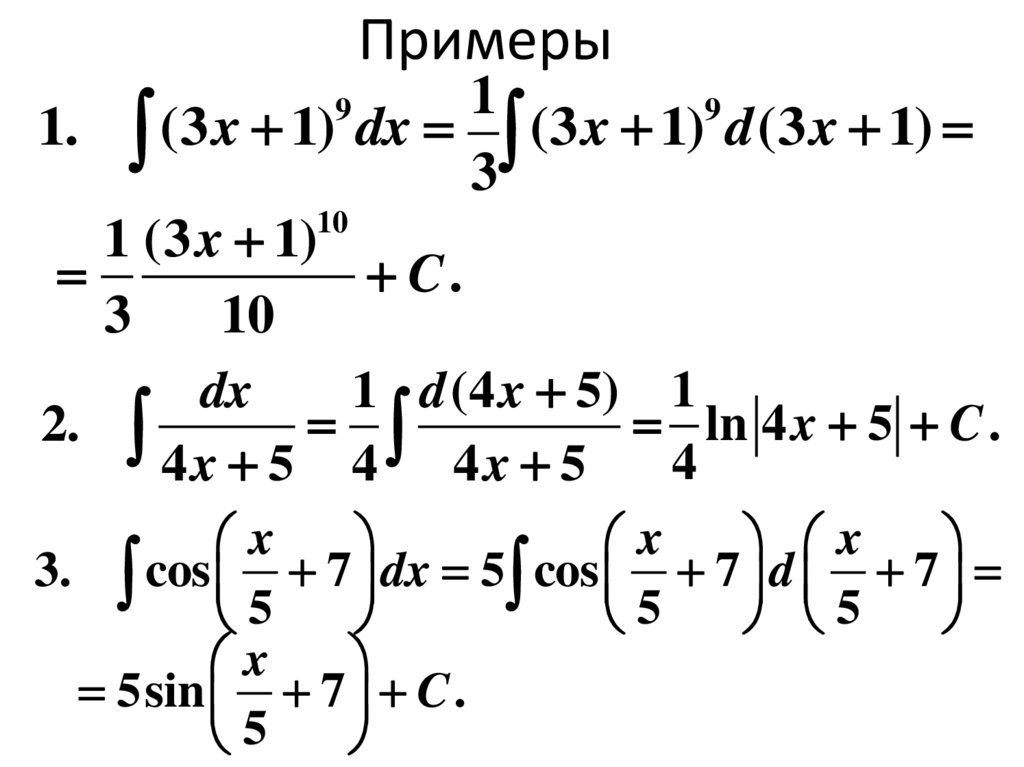









 Математика
Математика








