Похожие презентации:
Неопределенный интеграл. Неопределенный интеграл и его свойства
1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Неопределенный интеграл и его свойства.2. 1.1. Первообразная функция
y F ( x )ОПР. Функция
называется
первообразной для функции y f ( x ) на
данном промежутке (a;b), если для любого
x
из этого промежутка
F '( x ) f ( x ) или dF ( x ) f ( x )dx .
Пример. Первообразной для функции
f ( x) x
2
1 3
на всей числовой оси является F ( x ) x C
3
C const так как 1 3
2
x
C
x
.
3
3.
Теорема 1.1. Если функция f(x) непрерывнана данном интервале, то на этом интервале
она имеет первообразную.
Теорема 1.2. Если функция F(x) является
первообразной функции f(x) на (a;b), то
множество всех первообразных для f(x)
задается формулой F(x)+C, где C −
постоянная.
4. 1.2. Неопределенный интеграл
ОПР. Совокупность всех первообразныхF ( x ) C для данной функции f ( x )
называется ее неопределенным интегралом
и обозначается
f ( x )dx F ( x ) C ,
где C
– произвольная постоянная.
5.
Знакназывается интегралом, функция
f (x) – подынтегральной функцией,
f ( x)dx – подынтегральным выражением,
x
– переменной интегрирования.
Операция нахождения неопределенного
интеграла для данной функции называется
интегрированием этой функции.
Интегрирование – операция, обратная
операции дифференцирования.
6. Основные свойства неопределенного интеграла
1. Дифференциал от неопределенногоинтеграла
равен
подынтегральному
выражению:
d f ( x )dx f ( x )dx
7.
2.Производная
интеграла
равна
функции:
неопределенного
подынтегральной
f ( x )dx f ( x ).
Таким образом,
правильность интегрирования проверяется
дифференцированием!
8.
3.Неопределенный
интеграл
от
дифференциала некоторой функции равен
сумме этой функции и произвольной
постоянной:
dF
(
x
)
F
(
x
)
C
.
9.
4. Постоянный множитель можно выноситьза знак интеграла:
af
(
x
)
dx
a
f
(
x
)
dx
.
10.
5.Неопределенный
интеграл
от
алгебраической суммы конечного числа
непрерывных
функций
равен
алгебраической сумме интегралов от
слагаемых функций:
f ( x ) g( x ) dx f ( x )dx g( x )dx .
11.
6. Если f ( x ) dx F ( x ) C , тоf (u) du F (u) C ,
где u ( x )
− произвольная функция,
имеющая непрерывную производную.
Данное
свойство
называется
инвариантностью
неопределенного
интеграла.
12.
При вычислении неопределенного интегралаиспользуют формулу:
1
f (ax b)dx a F (ax b) C , a 0.
13. Таблица простейших интегралов
1. 0 du C ;1
2. 1 du u C ;
u
1
1
3. u du
C , 1; 4. 2 du C ;
u
u
1
1
1
5. du 2 u C ;
6. du ln u C ;
u
u
u
a
u
u
u
8.
e
du
e
C;
7. a du
C;
ln a
9. sin udu cos u C ;
10. cos udu sin u C ;
1
11. 2 du tgu C ;
cos u
1
12. 2 du ctgu C ;
sin u
14.
11
u
13. 2
du arctg C ;
2
u a
a
a
1
u
14.
du arcsin C ;
2
2
a
a u
du
1
u a
15. 2
ln
C;
2
u a
2a u a
16.
du
u2 a 2
2
2
ln u u a C .
15.
Вычисление интегралов с помощьюпреобразования
подынтегрального
выражения к табличной форме и
использования свойств неопределенного
интеграла называется непосредственным
интегрированием.
Вспомогательные сведения
m
n
1. a a a
m n
1
n
a ;
n
a
; 3.
m
a
m n
2.
a ;
n
a
4.
n
m
a a
m
n
.
16. Пример 1. Используя таблицу и свойства интегралов, найти интегралы.
5 1dx
x
5
1. 5 x dx (ô î ðì óëà (3))=
C
x
5 1
1
C.
4
4x
2.
(2 x 7 )dx 2 xdx 7 dx
x
x
2
x
x
x
7
7
2
(ô î ðì óëû (3), (7))= 2
C x
C.
2 ln 7
ln 7
17.
52
x
3. x dx dx (ô î ðì óëà (3))=
5
5
1
2
7
x
x 2
=
C
C.
5 1
7
2
2
dx
4. 2
x 16
dx
(ô î ðì óëà (13))= 2
2
x 4
1
x
arctg C .
4
4
18.
5.6.
dx
x 25
2
dx
9 x
2
ln x x 2 25 C .
dx
x
32 x 2 arcsin 3 C .
19. 1.3. Основные методы вычисления неопределенных интегралов
Непосредственное интегрированиеМетод интегрирования, при котором
данный интеграл путем тождественных
преобразований подынтегральной функции
(или выражения) и применения свойств
неопределенного интеграла приводится к
одному
или
нескольким
табличным
интегралам, называется непосредствен-ным
интегрированием.
20.
При сведении данного интеграла ктабличному часто используется следующее
преобразование дифференциала (операция
«подведения под знак дифференциала»).
Например:
f ( u)du d ( f ( u))
du d ( u b ), b const ;
1
du d (au b ), a 0, a const ;
a
cos udu d (sin u).
21. Интегрирование заменой переменной
Метод замены переменной (методподстановки) состоит в преобразовании
интеграла f(x)dx
в другой интеграл
f(u)du,
который вычисляется проще, чем исходный.
22. Интегрирование по частям
Формулаudv uv vdu,
где u u( x ) и v v ( x ) – дифференцируемые
функции, называется
формулой интегрирования по частям.
Метод интегрирования по частям
целесообразно применять, если
vdu
более прост в вычислении, чем
udv
.
23. Некоторые типы интегралов, которые можно вычислять методом интегрирования по частям
mxmx
P
(
x
)
a
dx ,
1. Интегралы вида Pn ( x )e dx , n
P ( x )sin mxdx, Pn ( x )cos mxdx ,
n
где Pn ( x ) − многочлен, m − число.
Здесь полагают u Pn ( x ),
за dv обозначают остальные сомножители.
24.
2. Интегралы вида Pn ( x ) ln xdx , Pn ( x )arcsin xdx ,P ( x )arccos xdx , P ( x )arctgxdx , P ( x )arcctgxdx.
n
n
n
Pn ( x )dx dv
Здесь полагают
за
u
обозначают остальные
ax
ax
сомножители.
e
cos
bxdx
,
e
sin bxdx ,
3. Интегралы вида
ax
где a и b − числа.
e .
За u можно принять функцию













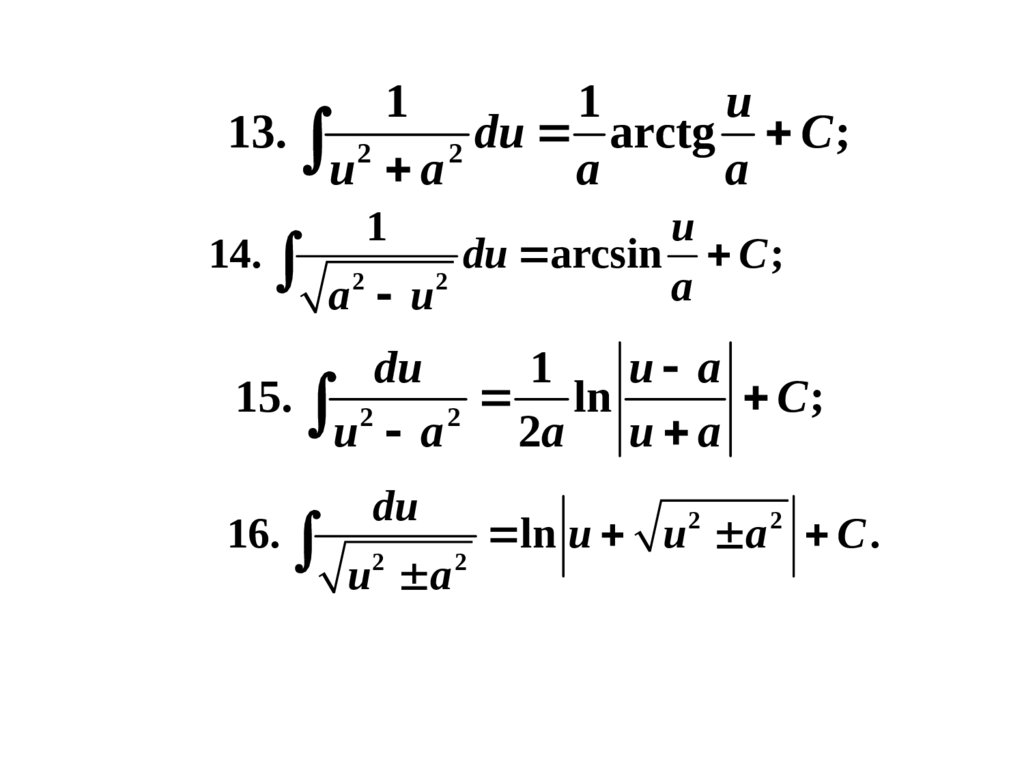


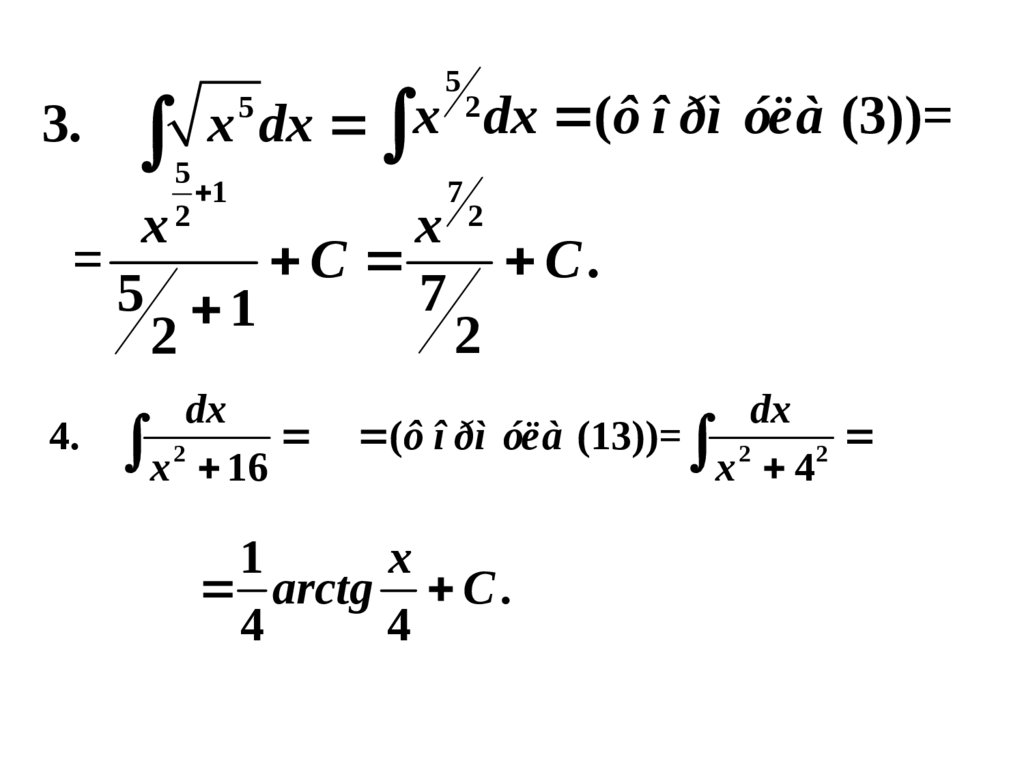







 Математика
Математика








