Теория движения военных колесных машин. Лекция 6

1.

Слайды к лекциям по курсу
ТЕОРИЯ ДВИЖЕНИЯ
ВОЕННЫХ КОЛЕСНЫХ МАШИН
Лекция 6

2.

Силовая установка характеризуется внешней
скоростной характеристикой: NДВ(nДВ) и MДВ(nДВ)

3.

Заводские характеристики силовых установок,
получаемую на стендовом оборудовании не
учитывают мощность необходимую для привода
дополнительного
оборудования
(вентилятор,
генератор, кондиционер, гидроусилитель и т.д.).
Потери на дополнительное оборудование для
двигателя могут составлять до 10%, они
учитываются с помощью коэффициента снимаемой
мощности kснN.
M дв-тр kснN M дв
N дв-тр kснN N дв

4.

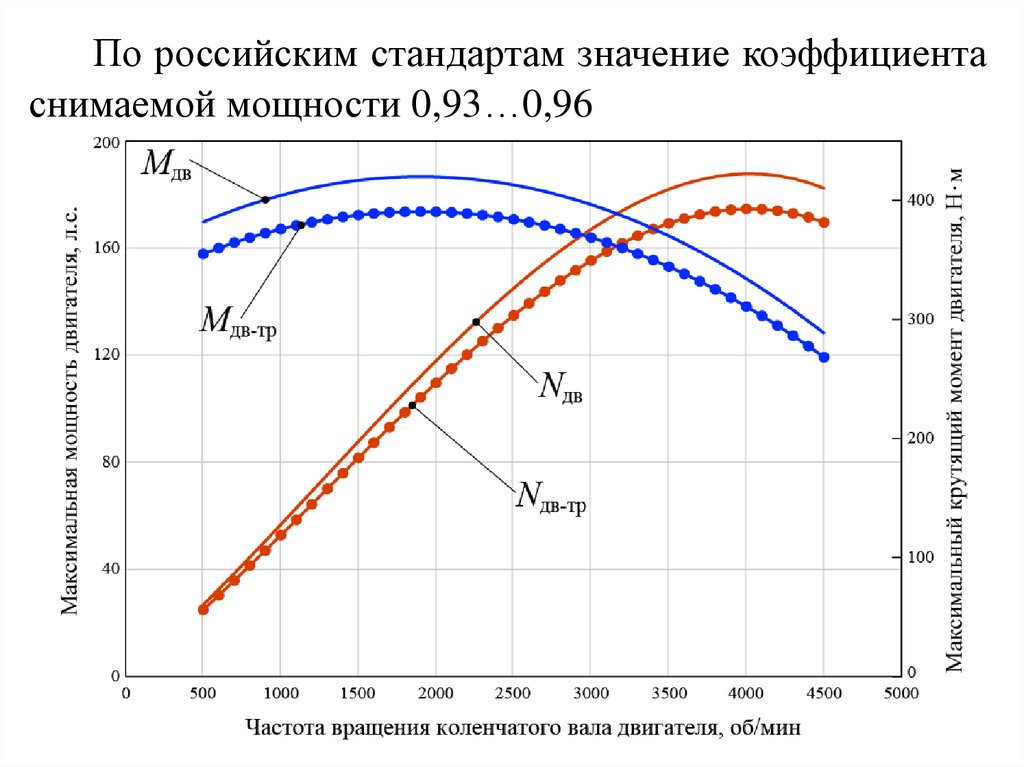
По российским стандартам значение коэффициента
снимаемой мощности 0,93…0,96

5.

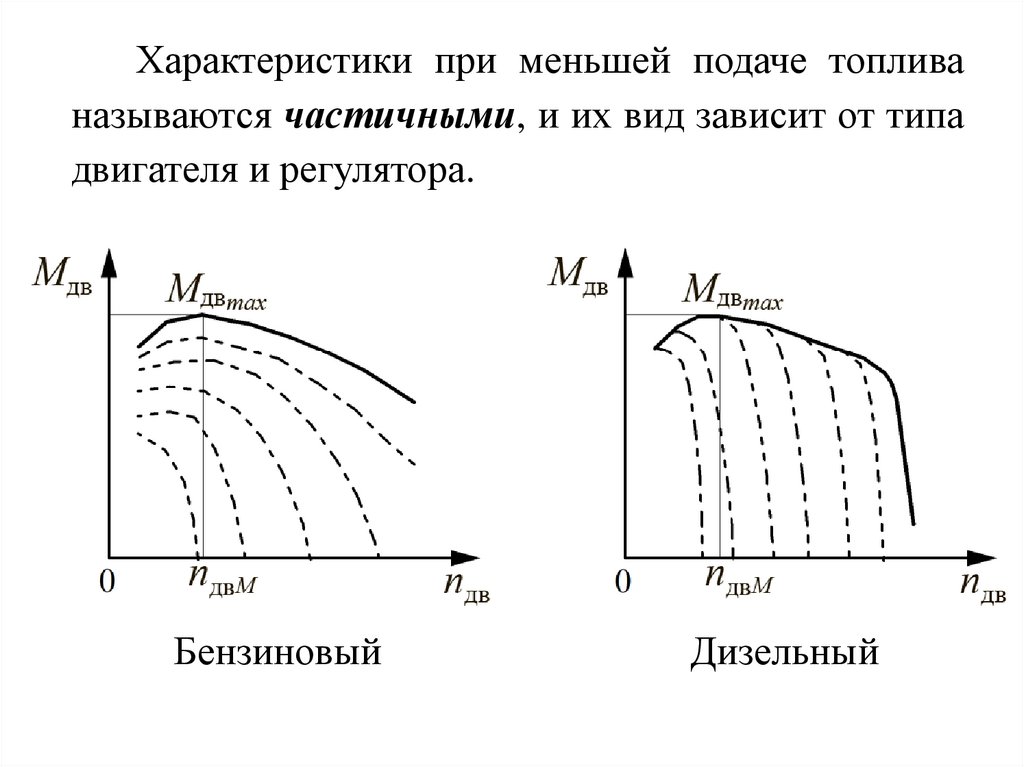
Характеристики при меньшей подаче топлива
называются частичными, и их вид зависит от типа
двигателя и регулятора.
Бензиновый
Дизельный

6.

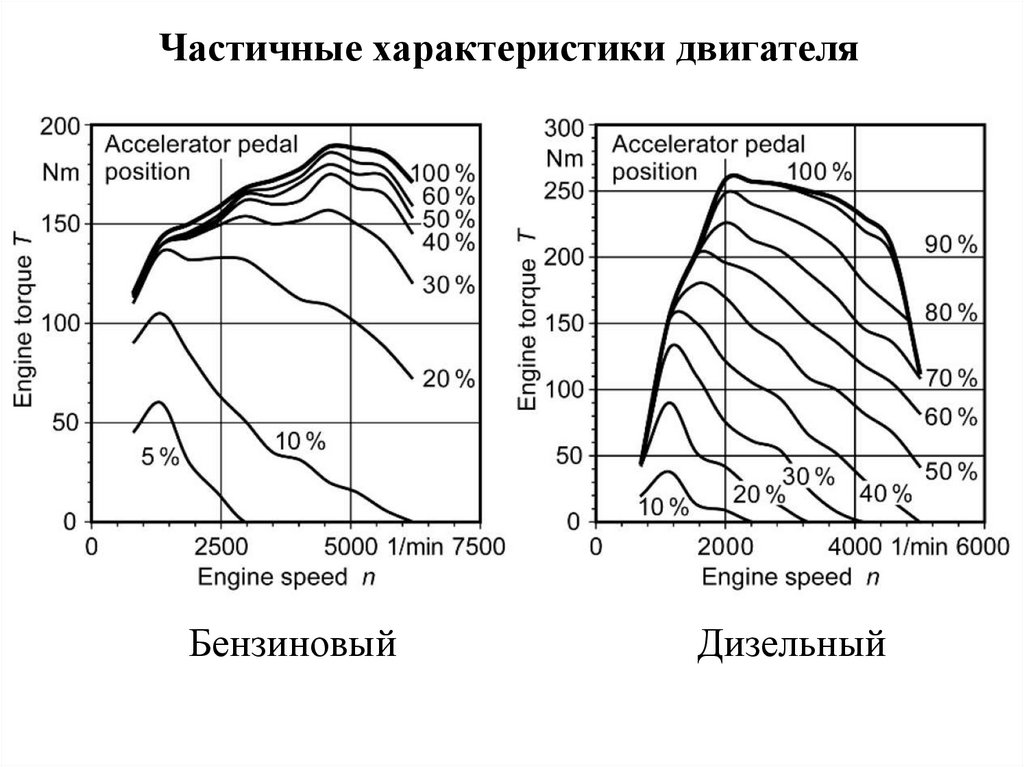
Частичные характеристики двигателя
Бензиновый
Дизельный

7.

Частичная характеристика двигателя

8.

Текущие значения Nдвi и M двi определяют по
экспериментальной ВСХ двигателя или приближенно
с помощью эмпирических зависимостей по базовым
точкам:
M двi
N двi
60 N дв max
2 π nдвN
nдвi
nдвi
a b
c
n
nдвN
двN
n
nдвi
двi
N дв max a
b
n
nдвN
двN
2
2
nдвi
c
n
двN
3

9.

a, b и c – коэффициенты, зависящие от
коэффициентов приспособляемости двигателя.
Коэффициент приспособляемости по оборотам
kдв n= nдвN / nдвM
Коэффициент приспособляемости по моменту
k дв M = Мдвmax / MдвN

10.

В механической части трансмиссии происходят
деформации
и
перемещения
элементов
и,
следовательно, возникают сопротивления.
Принято рассматривать упругие сопротивления
и сопротивления потерь.

11.

Момент упругого сопротивления:
M тр у Стрij φтрi φтрj
Cтрij - угловая жесткость валов на участке от i-го до j-го
сечений;
φтрi , φтрj - углы поворота валов в i-ом и j-ом сечениях.

12.

Сопротивления
связанные
с
механической
потерь
–
сопротивления,
необратимыми
превращениями
энергии
в теплоту. Их момент
принято представлять в виде двух составляющих:
пот M тр
пот
M тр пот M тр
Постоянная
Переменная
(динамическая)

13.

Постоянная
составляющая
момента
сопротивления при постоянной угловой скорости
вращающихся деталей ωтрi = const и обусловлена
силовыми и скоростными потерями.
Силовые потери зависят от передаваемого
момента и вызываются главным образом трением
между деталями.
Скоростные зависят от угловой скорости валов и
шестерен и вызываются потерями на размешивание
и разбрызгивание масла в редукторах.

14.

Переменная
(динамическая)
составляющая
момента сопротивления обусловлена колебаниями
деталей и зависит от частоты изменения момента,
конструктивных и эксплуатационных факторов.
Ее значение принимается пропорциональной
разнице угловых скоростей деталей соответственно
на входе ωтрi
и выходе ωтрj
участка, в котором
определяются потери:
пот kтрij ωтрi ωтрj
M тр
kтрij – коэффициент демпфирования.

15.

При отсутствии данных о kтрij потери в трансмиссии
оценивают коэффициентом полезного действия η.
Основные узлы КМ имеют следующие значения КПД:
Агрегат
Величина η
Обозначение
Коробка передач
0,95 – 0,98
ηкп
Раздаточная коробка
0,95 – 0,98
ηрк
Главная передача
0,93 – 0,97
ηгп
Колесный редуктор
0,96 – 0,98
ηкр
Карданная передача
0,99
ηкард

16.

Уравнения прямолинейного движения КМ
В наиболее общем случае колесная машина совершает
весьма сложные движения. Прежде всего нельзя строго
говорить о движении машины в целом, так как отдельные
ее части перемещаются одна относительно другой.
1) валы и зубчатые колеса вращаются
осей, расположенных в картерах;
2) колеса и мосты перемещаются в
плоскости относительно корпуса;
3) колеса, кроме того, поворачиваются
шкворней и т.д.;
4) корпус совершает поступательные
вдоль трех координатных осей и угловые
вокруг них.
относительно
вертикальной
относительно
перемещения
перемещения

17.

Уравнения прямолинейного движения КМ
Колесная машина представляет собой сложную
многомассовую систему. Рассматривать все движения
этой системы одновременно в большинстве случаев
нецелесообразно из-за громоздкости получаемой
системы уравнений.
Для решения различных задач можно делать те
или иные упрощения, учитывая лишь главные
движения системы для соответствующих случаев,
если при этом пренебрежение остальными не вносит
существенной ошибки в результат.

18.

Уравнения прямолинейного движения КМ
Прямолинейным будем называть такое движение
КМ, при котором в вертикальной продольной плоскости
симметрии машины, проходящей через середину колеи,
основное перемещение происходит в направлении оси
X, а дополнительное (при колебаниях на неровностях
дороги) – в направлении оси Z. Движения в поперечной
плоскости отсутствуют.
При движении по твердой плоской ОП можно
принять, что все части машины перемещаются в
направлении оси X с одинаковой скоростью,
вертикальные
перемещения
отсутствуют,
соответствующие детали двигателя, трансмиссии и
колеса совершают вращательные движения.

19.

Уравнения прямолинейного движения КМ
Рассматривается уравнение изменения кинетической
энергии системы:
k
m
i 1
j 1
dWкин dAвнешi dAвнутj
dWкин – дифференциал кинетической энергии системы;
dAвнешi – дифференциалы элементарных работ внешних
сил на i-м перемещении, 1 ≤ i ≤ k;
dAвнутj – дифференциалы элементарных работ
внутренних сил на j-м перемещении, 1 ≤ j ≤ m.

20.

Уравнения прямолинейного движения КМ
Кинетическая энергия КМ представляет собой сумму
кинетической энергии Wкин m ее массы, поступательно
движущейся вдоль оси Xc, и кинетической энергии Wкин J
вращающихся частей и узлов:
Wкин Wкин m Wкин J
Wкин m 0,5 mм v
2
мx
nк
2
2
2
0,5 J дв дв J тр j тр j J к i к i
j 1
i 1
nтр
Wкин J

21.

Уравнения прямолинейного движения КМ
mм – масса колесной машины, кг;
vмx – линейная скорость, м/с;
Jдв, Jтрj, Jкi – моменты инерции вращающихся и
приведенных к ним частей двигателя, деталей
трансмиссии, колес, кг∙м2;
ωдв, ωтрj, ωкi – угловые скорости выходного вала
двигателя, деталей трансмиссии, колес, с-1;
ωдв = dφдв/dt;
ωтрj = dφтрj/dt;,
ωкi = dφкi/dt.

22.

Уравнения прямолинейного движения КМ
Если пренебречь моментом инерции трансмиссии ,то
получим:
dWкин m mм vмx dvмx
nк
dWкин J J дв дв d дв J к i к i d к i
i 1

23.

Уравнения прямолинейного движения КМ
Сумма
элементарных
работ
внешних
сил
направленных против вектора скорости движения КМ:
k
dA
i 1
внешi
(Pfшм Pw Pм x Pпц x Pfп )ds
ds – элементарное перемещение КМ по продольной
оси Xc;
– приведенная к колесу эквивалентная сила
сопротивления
движению в подвеске при
колебаниях КМ.
Pf
п

24.

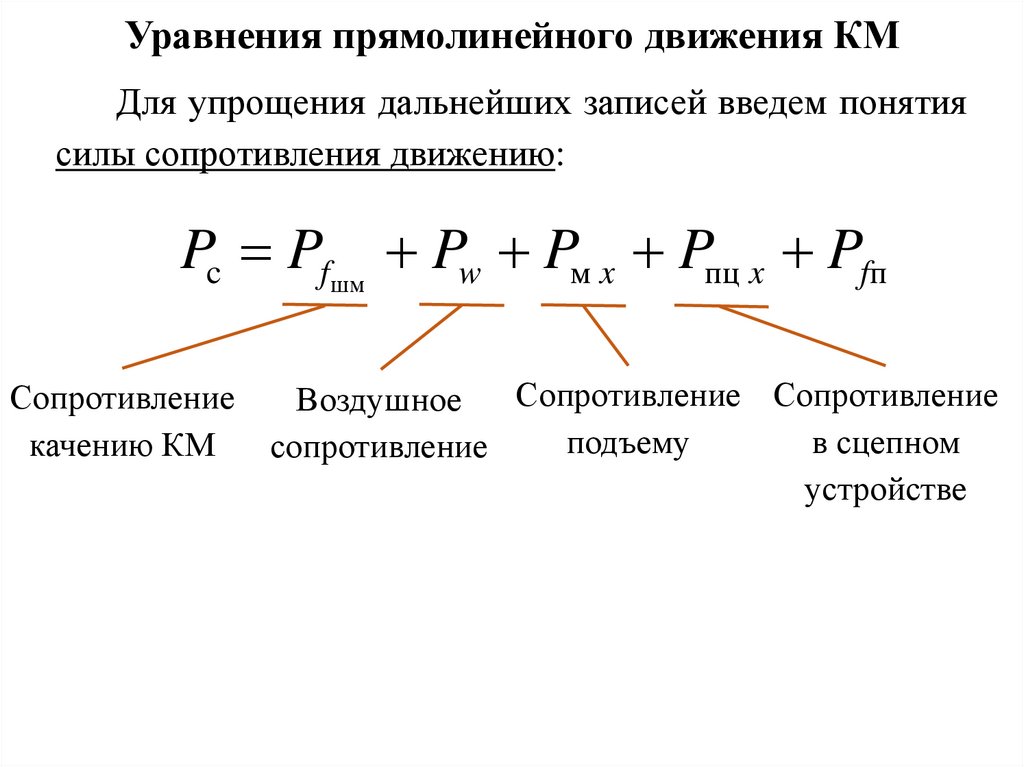
Уравнения прямолинейного движения КМ
Для упрощения дальнейших записей введем понятия
силы сопротивления движению:
Pc Pfшм Pw Pм x Pпц x Pfп
Сопротивление
качению КМ
Сопротивление Сопротивление
Воздушное
подъему
в сцепном
сопротивление
устройстве

25.

Уравнения прямолинейного движения КМ
Элементарная работа внутренних сил:
m
dA
j 1
внутj
dAдв dAтр M дв d дв (M дв M дв )(1 тр )d дв
Момент, поступающий
в трансмиссию (Mдв-тр)
Потери в
трансмиссии
dAдв – полезная работа двигателя
dAтр – работа сил сопротивлений в трансмиссии КМ
M дв J дв дв

26.

Уравнения прямолинейного движения КМ
Преобразуем некоторые кинематические параметры:
dφдв = ωдв dt;
ωдв = uтр ωк;
ωк = vмx/rк.
При отсутствии непосредственного скольжения
(Rx ≤ (0,4…0,6) φ Rzi) радиус качения rк = rк0.
При больших продольных реакциях и наличии
скольжения rк = rк0 (1 - sбj).

27.

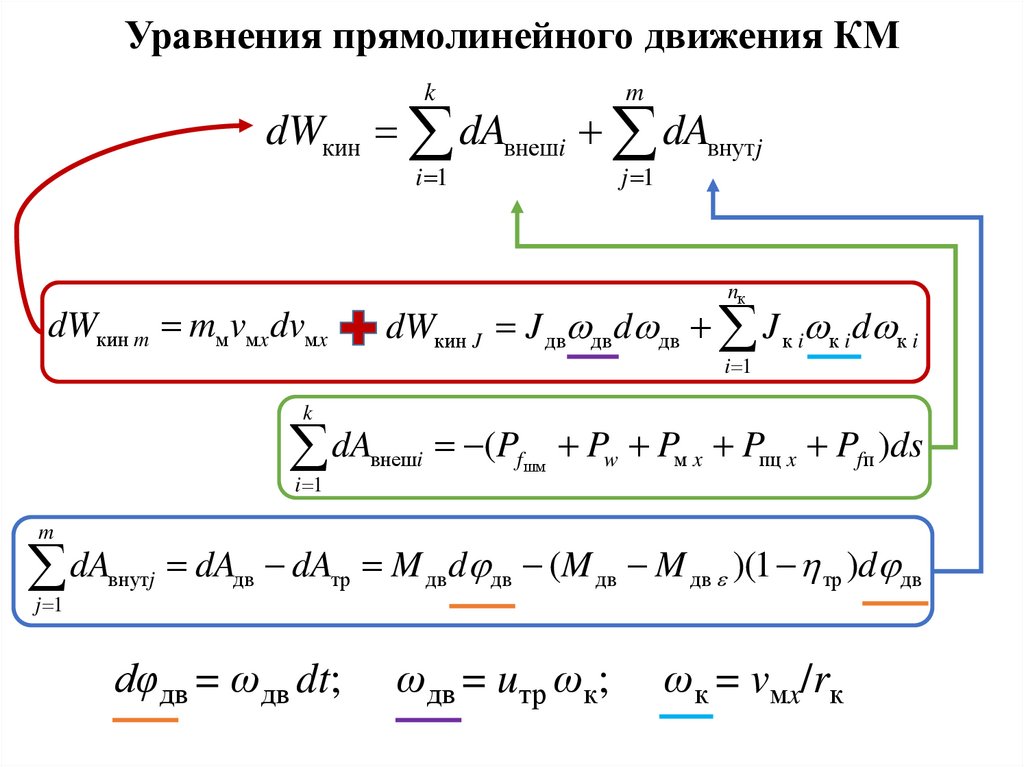
Уравнения прямолинейного движения КМ
k
m
i 1
j 1
dWкин dAвнешi dAвнутj
nк
dWкин J J дв дв d дв J к i к i d к i
dWкин m mм vмx dvмx
i 1
k
dA
i 1
m
dA
j 1
внутj
внешi
(Pfшм Pw Pм x Pпц x Pfп )ds
dAдв dAтр M дв d дв (M дв M дв )(1 тр )d дв
dφдв = ωдв dt;
ωдв = uтр ωк;
ωк = vмx/rк

28.

Уравнения прямолинейного движения КМ
Разделив обе части полученного равенства на уравнение
ds = vмx dt
после преобразований получим
2
2
2
aм x mм J двuтр тр /rк J кi /rк M дв-трuтр тр /rк Pc
i 1
nк
где aм x
dvм x
dt

29.

Уравнения прямолинейного движения КМ
Для упрощения записи вводится понятие
коэффициента учета вращающихся масс δвр. Он
показывает во сколько раз сила, необходимая для
разгона с заданным ускорением aмx поступательно
движущихся и вращающихся масс КМ, больше силы,
необходимой для разгона только ее поступательно
движущихся масс:
вр 1
nк
J u J кi
2
дв тр тр
mм rк2
i 1

30.

Уравнения прямолинейного движения КМ
Тогда уравнение прямолинейного движения КМ
примет вид:
mм вр aмx
M дв-трuтр тр
rк
Pc
Полная окружная сила, поступающая на ведущие
колеса машины, определяется выражением:
Pкм
M дв-трuтр тр
rк0

31.

Уравнения прямолинейного движения КМ
Приведенную силу инерции КМ обозначим
Pин = mм δвр ax
Тогда при стационарном движении уравнение
прямолинейного движения преобразуется в
уравнение силового баланса:
Pкм Pc Pин Pfшм Pw Pм x Pпц x Pfп Pин

32.

Уравнения прямолинейного движения КМ
Если все члены уравнения тягового баланса
умножить на скорость движения vмx, то оно
преобразуется в уравнение мощностного баланса при
отсутствии непосредственного скольжения колес:
N км N дв-тр тр N fшм N w N мx N пц x N fп N ин
При наличии проскальзывания и rк ≠ 0
необходимая расчетная мощность определяется
приближенно по уравнению:
N км rк0 /rк
N км

33.

Уравнения прямолинейного движения КМ
Приведенные выше уравнения получены для
стационарного движения КМ с абсолютно жесткой
связью двигателя с ведущими колесами. При
нестационарных режимах работы необходимо
учитывать угловую жесткость и демпфирование валов
трансмиссии и шин.

34.

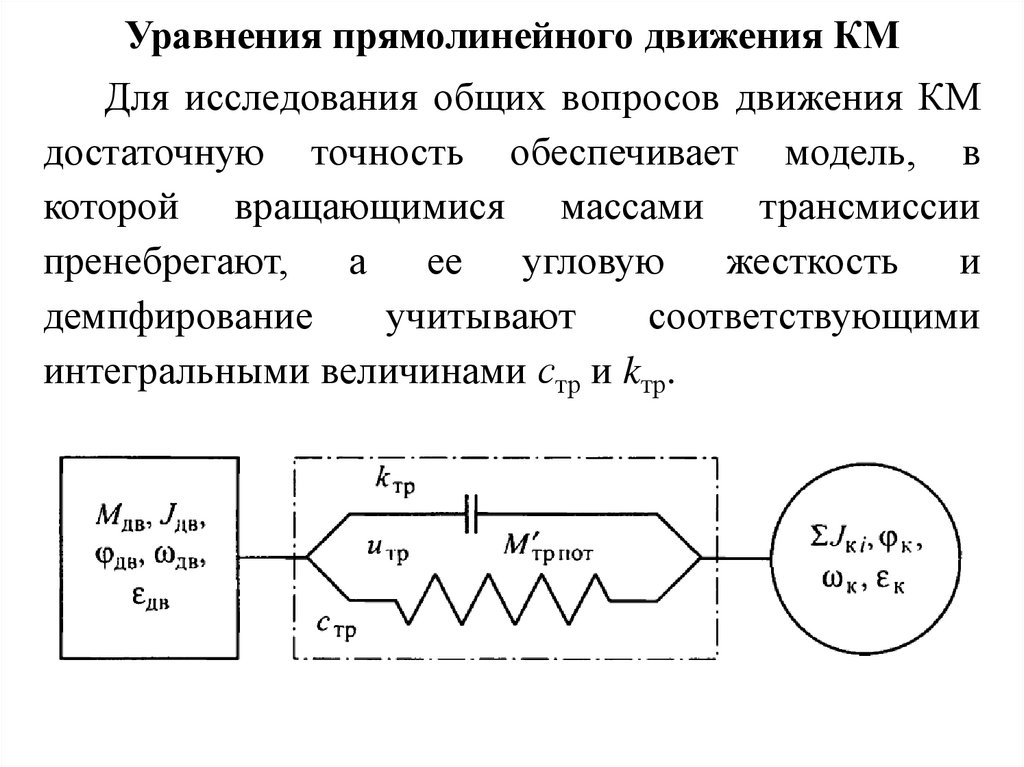
Уравнения прямолинейного движения КМ
Для исследования общих вопросов движения КМ
достаточную точность обеспечивает модель, в
которой вращающимися массами трансмиссии
пренебрегают,
а
ее
угловую
жесткость
и
демпфирование
учитывают
соответствующими
интегральными величинами стр и kтр.