Похожие презентации:
Теория движения военных колесных машин. Лекция 3
1.
Слайды к лекциям по курсуТЕОРИЯ ДВИЖЕНИЯ
ВОЕННЫХ КОЛЕСНЫХ МАШИН
Лекция 3
2.
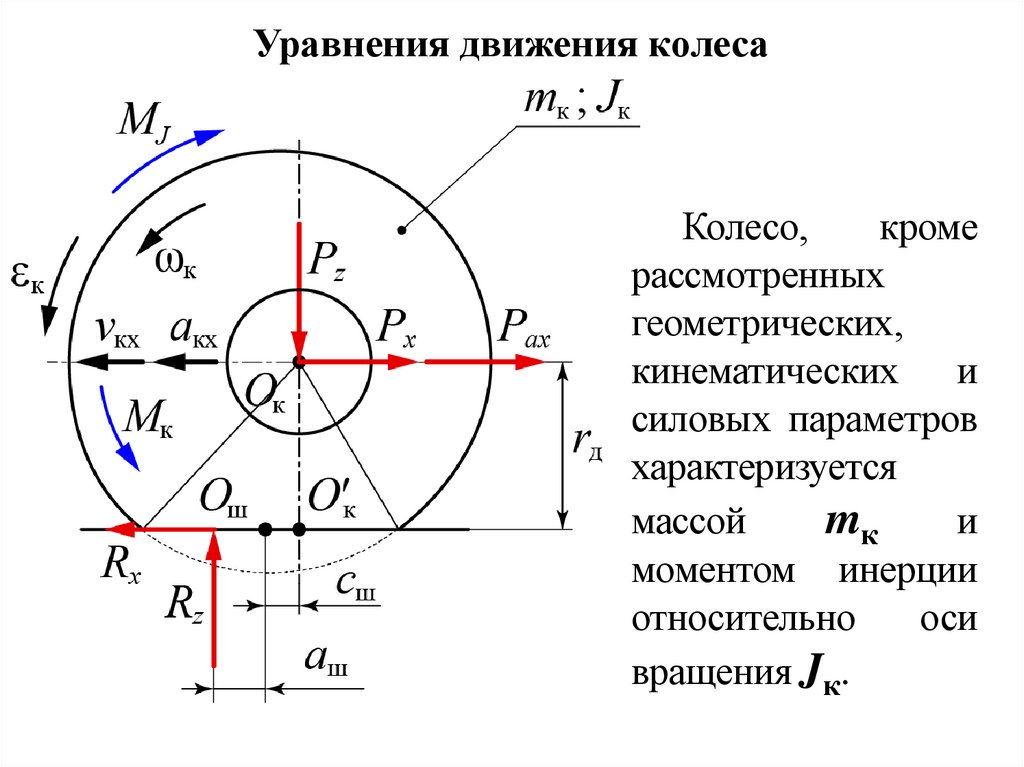
Уравнения движения колесаКолесо,
кроме
рассмотренных
геометрических,
кинематических и
силовых параметров
характеризуется
массой
mк
и
моментом инерции
относительно
оси
вращения Jк.
3.
Уравнения движения колесаaкx dvкx dt
Продольное ускорение
aкz dvкz dt
Вертикальное ускорение
dω к
εк
dt
Угловое ускорение
Pax mк aкx
Инерционная сила
M J J к εк
Инерционный момент
4.
Уравнения движения колесаPax Rx Px
Paz Rz Pz
*
Если
aкz 0
то
Rz Pz
M J M к Rx rд Rz aш cш
Ранее введено понятие момента сопротивления
качению в свободном режиме:
M f ш Rz aш
5.
Уравнение мощностного балансаM к ωк Rx vкx M J ωк M fш ωк Rx vs
Так как
а
vs vотн vкx ,
vотн ωк rк0
то после деления на ωк и преобразований получим
M к Rx rк0 M J M fш
6.
Уравнение мощностного балансаM к Rx rк0 M J M fш
Если рассмотреть это
уравнение и уравнение
равенства моментов (*), то
M J M к R x rд R z aш cш
*
можно выразить cш
cш Rx rк0 rд Rz
Но это справедливо для малых деформаций колеса, а есть
очень эластичные покрышки.
7.
Уравнения движения колесаВведем следующие понятия:
Pк M к rк0
Полная окружная сила
Pfш св M fш rк0
f ш св
Pfш св
Rz
аш
rк0
Сила сопротивления качению
в свободном режиме
Коэффициент сопротивления
качению в свободном режиме
8.
Уравнения движения колесаПроведем преобразования относительно εк
dωк aкx
εк
dt
rк
Угловое ускорение
И инерционного момента:
J к aкx
M J J к εк
rк
9.
Уравнения движения колесаУравнение баланса сил на колесе:
Pк Pfш св Px Pax M J rк0
или
Mк
J к aкx
f ш св Rz Px mк aкx
rк0
rк rк0
10.
Уравнение баланса сил на колесеMк
J к aкx
f ш св Rz Px mк aкx
rк0
rк rк0
1
2
3
Полная окружная сила затрачивается на:
Pfш св
1
Сопротивление качению шины
2
Создание силы тяги на оси колеса
3
Продольный разгон колеса (ускорение)
4
Раскрутку колеса
M J rк0
4
Px
Pax
11.
Уравнение баланса сил на колесеПолная окружная сила, подводимая от двигателя
через
трансмиссию
к
колесу,
может
быть
ограничена возможностью создания достаточной
продольной реакции:
Rx Px Pax
Rx ограничена реакцией (силой) сцепления:
R Rz
φ – коэффициент сцепления:
12.
Уравнение баланса мощностиJ к aкx к
M к к Px rк к f ш св Rz rк0 к mк aкx rк к
Rz rк0 к Sбj
rк
N к N тяг N fш N ax N J N S
13.
Уравнение баланса мощностиN к N тяг N fш N ax N J N S
Nк
N тяг
N fш
- подведенная к колесу мощность
N ax
NJ
NS
- мощность на разгон колеса
- тяговая мощность
- мощность на сопротивление качению
- мощность на раскрутку колеса
- мощность на скольжение (буксование) колеса
14.
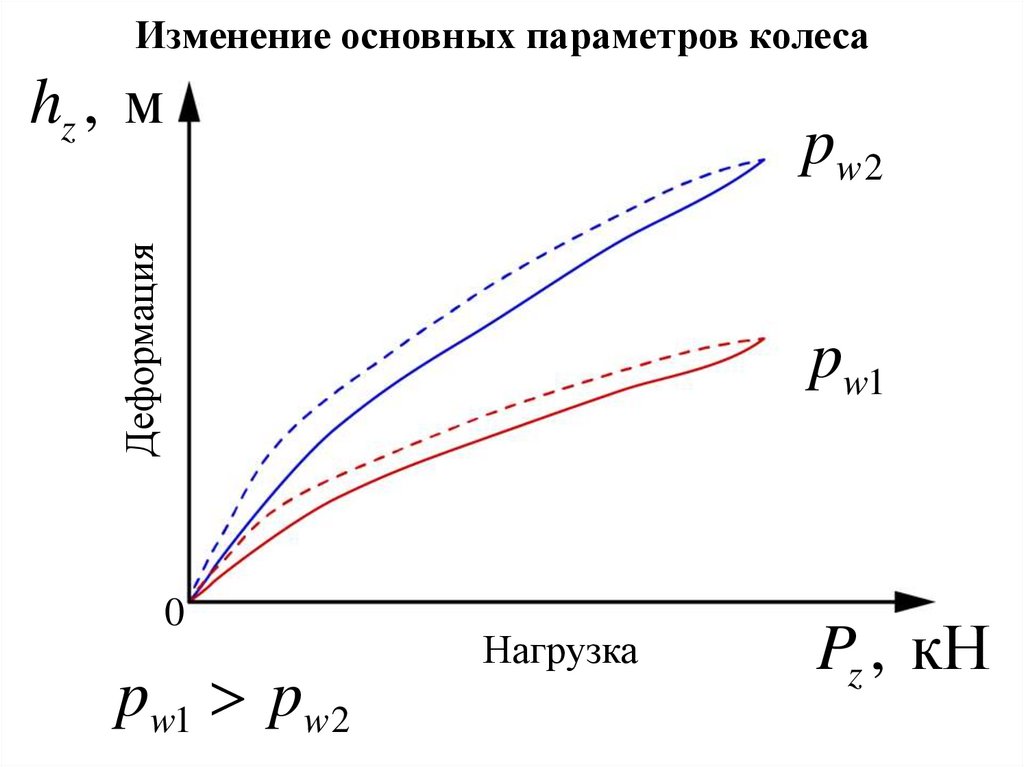
Изменение основных параметров колесаhz , м
Деформация
pw 2
pw1
0
pw1 pw 2
Нагрузка
Pz , кН
15.
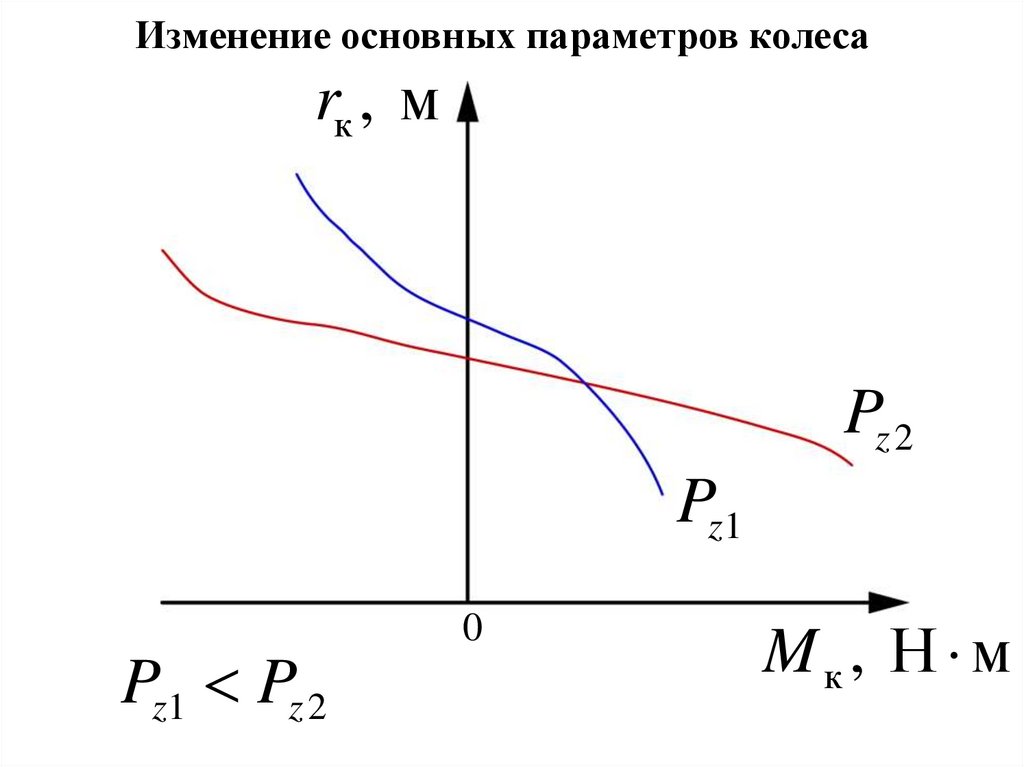
Изменение основных параметров колесаrк , м
Pz 2
Pz1
Pz1 Pz 2
0
Mк, Н м
16.
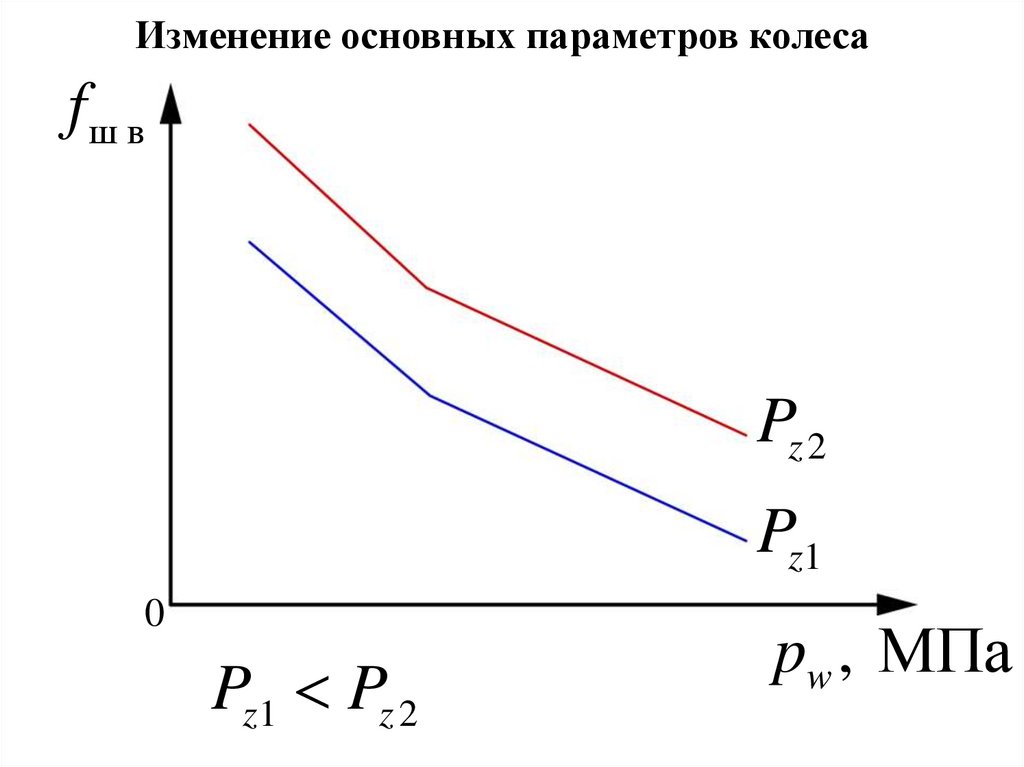
Изменение основных параметров колесаfш в
Pz 2
Pz1
0
Pz1 Pz 2
pw , МПа
17.
Безразмерные показатели колесаИх вводят для облегчения сравнения различных колес
1
f ш в Pfш в R
2
k Px k тяг Px Rz
Коэф. сопротивления качению
z в ведомом режиме
Коэф. продольной силы
Коэффициенты продольного
бj скольжения (см. ранее)
3
Sб , Sбу , S
4
k Rx Rx Rz
Коэф. продольной реакции
18.
Безразмерные показатели колеса5
fN
Коэф. подведенной мощности
Nк
Nк
fN
k тяг f N f
mк g vкx Pz vкx
6
fN f
fN f
Коэф. мощности сопротивлений
N к N тяг N fш N ax N J N S
Pz vкx
Pz vкx
19.
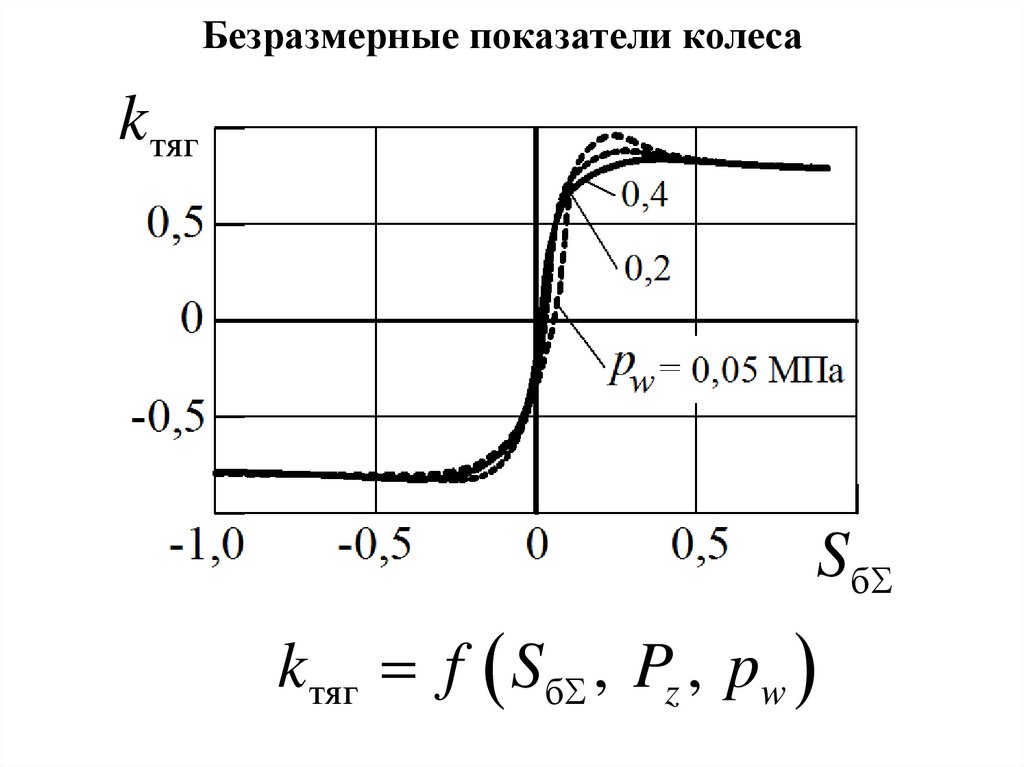
Безразмерные показатели колесаk тяг
S б
k тяг f Sб , Pz , pw
20.
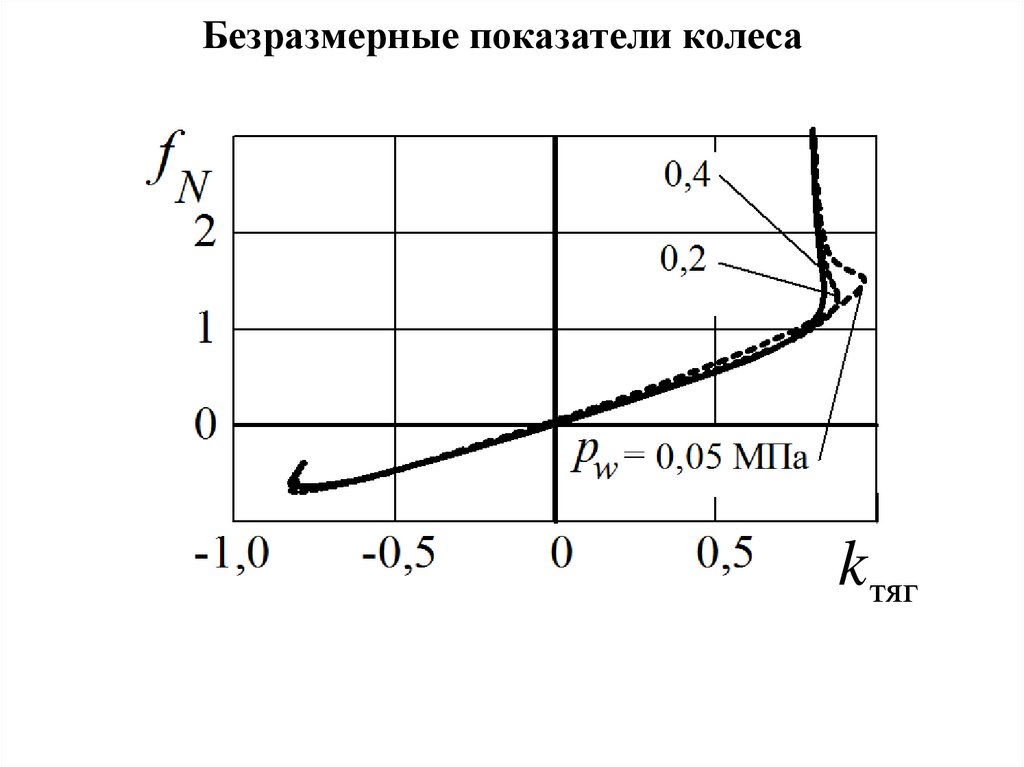
Безразмерные показатели колесаk тяг
21.
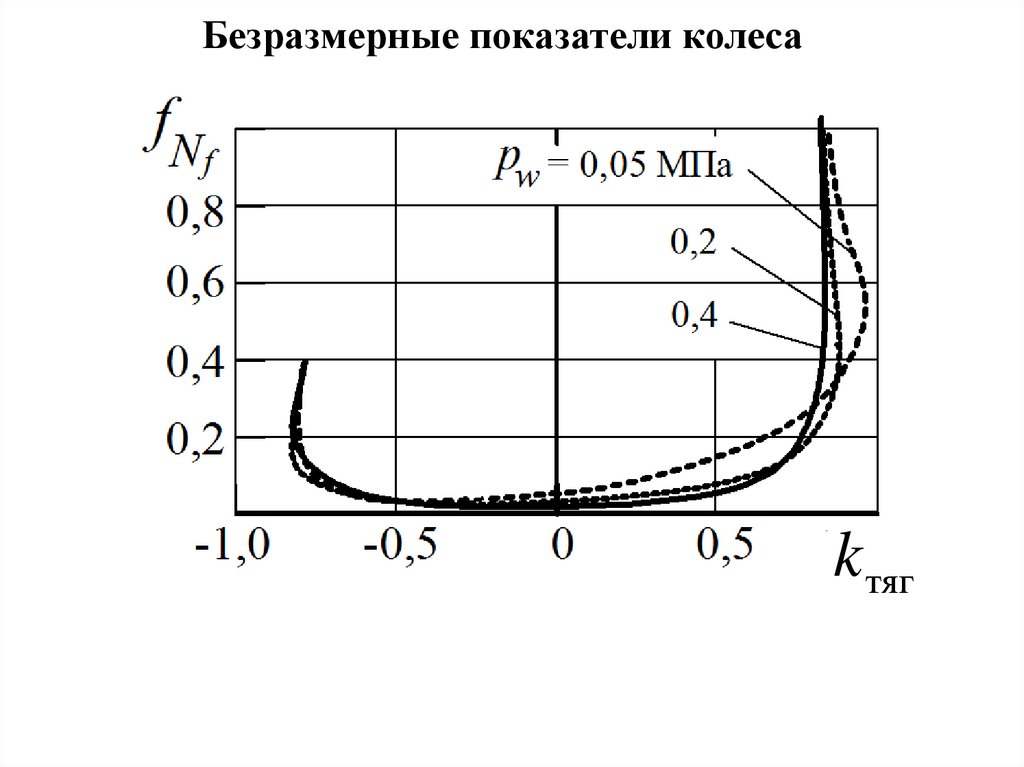
Безразмерные показатели колесаk тяг














 Физика
Физика Механика
Механика








